多叉树题目:N 叉树的层序遍历
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:N 叉树的层序遍历
出处:429. N 叉树的层序遍历
难度
4 级
题目描述
要求
给定一个 N 叉树的根结点 root \texttt{root} root,返回其结点值的层序遍历。
N 叉树在输入中按层序遍历序列化表示,每组子结点由空值 null \texttt{null} null 分隔(请参见示例)。
示例
示例 1:
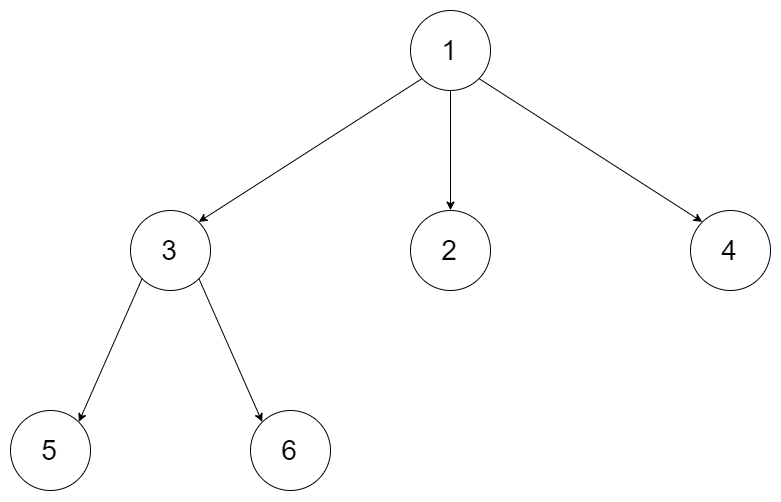
输入: root = [1,null,3,2,4,null,5,6] \texttt{root = [1,null,3,2,4,null,5,6]} root = [1,null,3,2,4,null,5,6]
输出: [[1],[3,2,4],[5,6]] \texttt{[[1],[3,2,4],[5,6]]} [[1],[3,2,4],[5,6]]
示例 2:
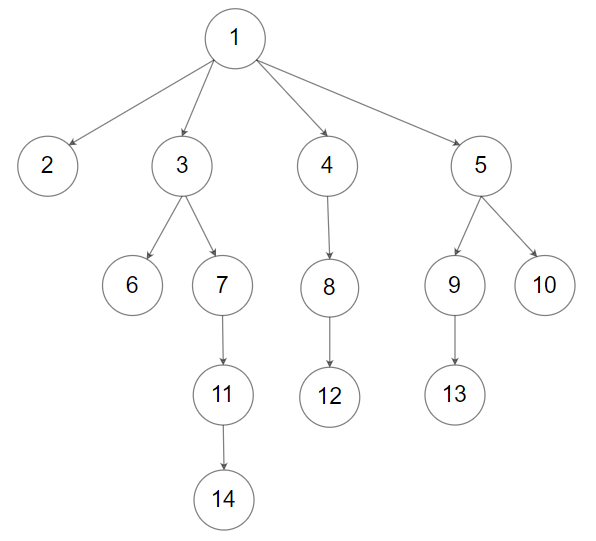
输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] \texttt{root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]} root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]] \texttt{[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]} [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
数据范围
- 树中结点数目在范围 [0, 10 4 ] \texttt{[0, 10}^\texttt{4}\texttt{]} [0, 104] 内
- N 叉树的高度小于或等于 1000 \texttt{1000} 1000
解法
思路和算法
层序遍历的方法为从根结点开始依次遍历每一层的结点,由于每一层与根结点的距离依次递增,因此可以使用广度优先搜索实现层序遍历。
广度优先搜索需要使用队列存储待访问的结点,初始时将根结点入队列。每次将一个结点出队列,然后将该结点的子结点入队列,直到队列为空时遍历结束。
由于这道题需要将结点值按照不同层分组,因此需要区分不同结点所在的层,确保每一轮访问的结点为同一层的全部结点。
初始时,队列内只有根结点,是同一层的全部结点。每一轮访问结点之前需要首先得到队列内的元素个数,此时队列内的元素为同一层的全部结点,然后访问这些结点,并将这些结点的子结点入队列。一轮访问结束之后,当前层的全部结点都已经出队列并被访问,此时队列内的元素为下一层的全部结点,下一轮访问时即可访问下一层的全部结点。使用上述做法,可以确保每一轮访问的结点为同一层的全部结点。
对于每一层维护一个结点值序列。遍历完每一层结点之后,将该层结点值序列添加到层序遍历序列中。
代码
class Solution {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> levelOrderTraversal = new ArrayList<List<Integer>>();if (root == null) {return levelOrderTraversal;}Queue<Node> queue = new ArrayDeque<Node>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> levelValues = new ArrayList<Integer>();int size = queue.size();for (int i = 0; i < size; i++) {Node node = queue.poll();List<Node> children = node.children;levelValues.add(node.val);for (Node child : children) {queue.offer(child);}}levelOrderTraversal.add(levelValues);}return levelOrderTraversal;}
}
复杂度分析
-
时间复杂度: O ( m ) O(m) O(m),其中 m m m 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( m ) O(m) O(m),其中 m m m 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 m m m。
相关文章:

多叉树题目:N 叉树的层序遍历
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:N 叉树的层序遍历 出处:429. N 叉树的层序遍历 难度 4 级 题目描述 要求 给定一个 N 叉树的根结点 root \texttt{root} root…...

时序数据库IoTDB:功能详解与行业应用
一文读懂时序数据库 IoTDB。 01 为什么需要时序数据库 解释时序数据库前,先了解一下何谓时序数据。 时序数据,也称为时间序列数据,是指按时间顺序记录的同一统计指标的数据集合。这类数据的来源主要是能源、工程、交通等工业物联网强关联行业…...
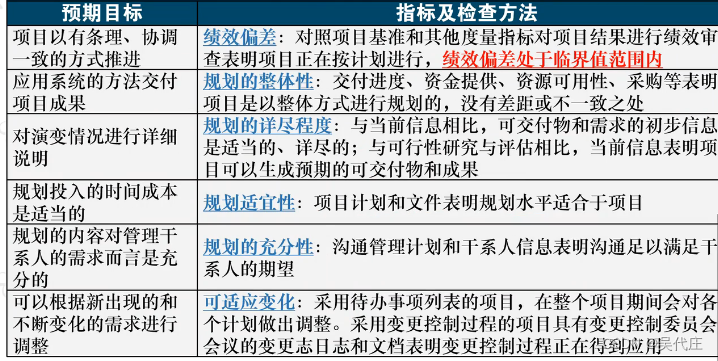
信息系统项目管理师——第18章项目绩效域管理(一)
本章节内容属于第四版新增知识,为PMBOK第七版专有,选择、案例、论文都会考,属于比较重要的章节。 选择题,稳定考3分左右,新教材基本考课本原话,需要多读课本,多刷题。 案例题,考的概…...
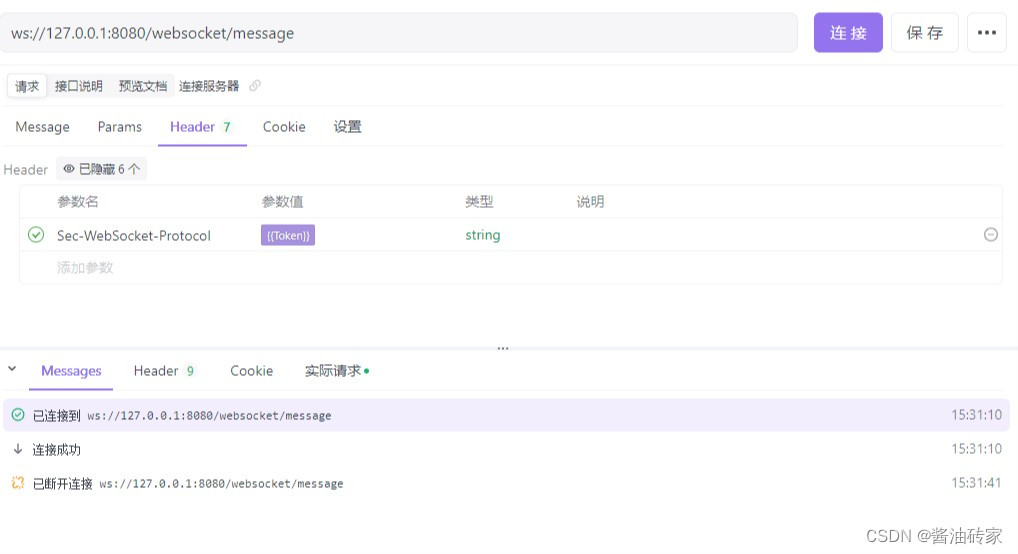
WebSocket用户验证
在WebSocket中,如何携带用户的验证信息 一、在OnMessage中进行验证 客户端在连接到服务器后,客户端通过发送消息,服务器端在OnMessage方法中,进行信息验证,这种方式需要将用户身份验证及接收用户消息进行混合处理&am…...
的优缺点有哪些?)
NOSQL(非关系型数据库)的优缺点有哪些?
优点: 高度灵活且可扩展:NoSQL数据库不受固定数据模型的限制,可以根据应用需求灵活设计数据结构,轻松应对大规模数据集。此外,它支持分布式架构,具有出色的水平扩展能力,能够高效地处理大量数据…...

个人推荐Redis比较好的一种使用规范
随着对个人项目的不断开发、迭代和重构,博主在这个过程中总结出了一套使用redis的较好的规范。主要包含Redis的key命名规范和Redis代码规范。 主要内容 主要包含以下几个内容: 同一应用的key在最前面添加统一的前缀,如应用名; 案…...

【教程】宝塔default.db占用空间几十g解决方法|宝塔占用磁盘空间特别大解决方法|宝塔磁盘被占满怎么清理
目录 一、前言二、排查问题三、解决方法 一、前言 用过宝塔创建网站,大家应该都非常熟悉,但是用随着用的时间越来越多,宝塔所占用的空间也越来越多,不停的加大数据盘都没有用,我原先买了30G够用了,随着时间…...

Unity类银河恶魔城学习记录11-15 p117 Ice and Fire item Effect源代码
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili IceAndFire_Controller.cs using System.Collections; using System.Coll…...

Qt QML的枚举浅用
QML的枚举用法 序言概念命名规则在QML定义枚举的规范 用法QML的枚举定义方法供QML调用的,C的枚举定义方法 序言 概念 QML的枚举和C的其实差不多,但是呢,局限比较多,首先不能在main.qml里定义,也不能在子项中定义。 …...

设计模式:单例模式六种实现
单例模式有多种实现方式,每种方式都有其设计思想、优缺点以及适用的使用场景。以下是一些常见的单例实现方式: 1. 懒汉式(线程不安全) 设计思想 这种实现方式采用了类加载的懒加载机制来保证单例只在第一次使用时被创建。 实现代码 public class Singleton {private s…...
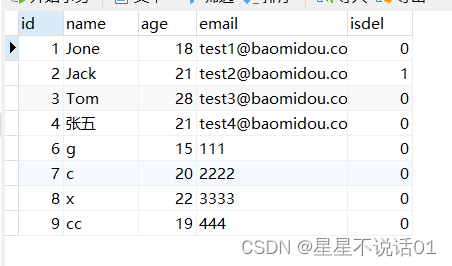
Mybatis-Plus05(分页插件)
分页插件 MyBatis Plus自带分页插件,只要简单的配置即可实现分页功能 1. 添加配置类 Configuration MapperScan("com.atguigu.mybatisplus.mapper") //可以将主类中的注解移到此处 public class MybatisPlusConfig {Bean public MybatisPlusIntercepto…...
python爬取B站视频
参考:https://cloud.tencent.com/developer/article/1768680 参考的代码有点问题,请求头需要修改,上代码: import requests import re # 正则表达式 import pprint import json from moviepy.editor import AudioFileClip, Vid…...
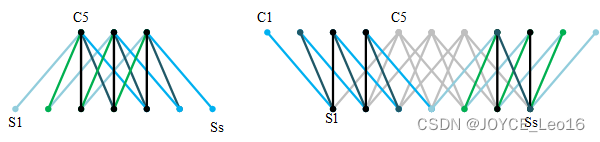
深度学习500问——Chapter05: 卷积神经网络(CNN)(2)
文章目录 5.6 有哪些池化方法 5.7 1x1卷积作用 5.8 卷积层和池化层有什么区别 5.9 卷积核是否一定越大越好 5.10 每层卷积是否只能用一种尺寸的卷积核 5.11 怎样才能减少卷积层参数量 5.12 在进行卷积操作时,必须同时考虑通道和区域吗 5.13 采用宽卷积的好处有什么 …...

基于单片机的测时仪系统设计
**单片机设计介绍,基于单片机的测时仪系统设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的测时仪系统设计是一个结合了单片机技术与测时技术的综合性项目。该设计的目标是创建一款精度高、稳定性强且…...
)
鸿蒙原生应用开发-网络管理Socket连接(三)
应用通过TLS Socket进行加密数据传输 开发步骤 客户端TLS Socket流程: 1.import需要的socket模块。 2.绑定服务器IP和端口号。 3.双向认证上传客户端CA证书及数字证书;单向认证只上传CA证书,无需上传客户端证书。 4.创建一个TLSSocket连接…...
【Java EE】关于Maven
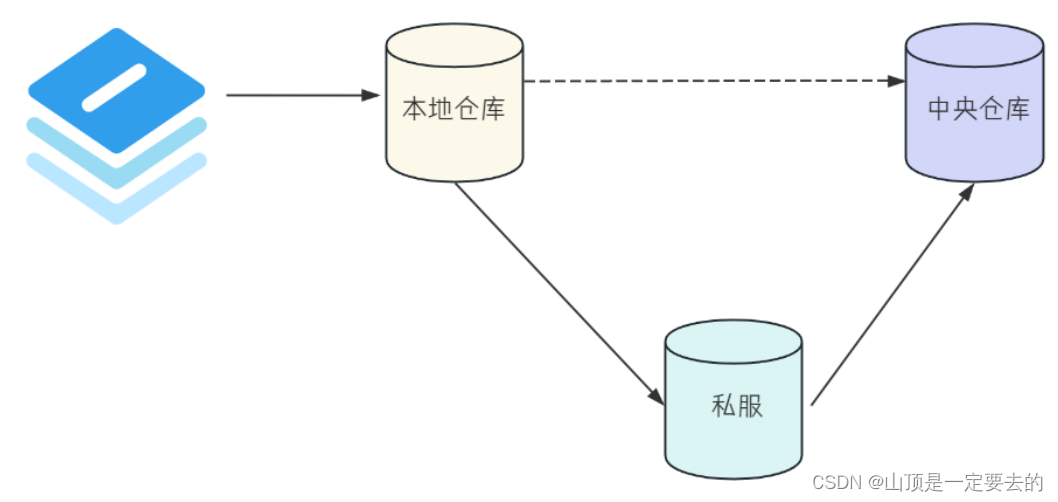
文章目录 🎍什么是Maven🌴为什么要学Maven🌲创建⼀个Maven项目🌳Maven核心功能🌸项目构建🌸依赖管理 🍀Maven Help插件🎄Maven 仓库🌸本地仓库🌸私服 ⭕总结 …...

每日一题:C语言经典例题之反转数
题目描述 给定一个整数,请将该数各个数位上的数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零。 题目描述 给定一个整数,请将该数各个数位上的数字反转得到一个…...

RESTfull接口访问Elasticsearch
【数据库的健康值】 curl -X GET "ip:9200/_cat/health" 【查看所有索引】 curl -X GET "ip:9200/_cat/indices?v" 【查看索引index_name】 curl -X GET "ip:9200/索引?pretty" 【创建索引/文档】 PUT "ip:9200/索引/文档id" {请…...

NoSQL之Redis
目录 一、关系型数据库与非关系型数据库 1.关系数据库 2.非关系数据库 2.1非关系型数据库产生背景 3.关系型数据库与非关系型数据区别 (1)数据存储方式不同 (2)扩展方式不同 (3)对事物性的支持不同 …...
)
double二分(P3743 小鸟的设备)
题目:P3743 小鸟的设备 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 代码: #include<bits/stdc.h> using namespace std; const int N2e510; double a[N],b[N]; int n; double p;bool check(double mid) {double sum0.0;for(int i1;i<n;i){if(a[i]*mi…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
