每日一题:C语言经典例题之反转数
题目描述
给定一个整数,请将该数各个数位上的数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零。
题目描述
给定一个整数,请将该数各个数位上的数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零。
输入
一个十进制整数。
输出
对应的反转数。
样例输入
-690样例输出
-96代码:
#include <stdio.h>
int main()
{int a,d,f=0;scanf("%d", &a);if (a >(-10) && a < 10){printf("%d", a);}else{do{d = a % 10;f = f * 10 + d;a = a / 10; if (a < 10 &&a>(-10)){int g = f * 10 + a;printf("%d",g);}} while (a >10 || a<(-10));}return 0;
}相关文章:

每日一题:C语言经典例题之反转数
题目描述 给定一个整数,请将该数各个数位上的数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零。 题目描述 给定一个整数,请将该数各个数位上的数字反转得到一个…...

RESTfull接口访问Elasticsearch
【数据库的健康值】 curl -X GET "ip:9200/_cat/health" 【查看所有索引】 curl -X GET "ip:9200/_cat/indices?v" 【查看索引index_name】 curl -X GET "ip:9200/索引?pretty" 【创建索引/文档】 PUT "ip:9200/索引/文档id" {请…...

NoSQL之Redis
目录 一、关系型数据库与非关系型数据库 1.关系数据库 2.非关系数据库 2.1非关系型数据库产生背景 3.关系型数据库与非关系型数据区别 (1)数据存储方式不同 (2)扩展方式不同 (3)对事物性的支持不同 …...
)
double二分(P3743 小鸟的设备)
题目:P3743 小鸟的设备 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 代码: #include<bits/stdc.h> using namespace std; const int N2e510; double a[N],b[N]; int n; double p;bool check(double mid) {double sum0.0;for(int i1;i<n;i){if(a[i]*mi…...

【独立开发前线】Vol.36 为什么从2023年开始,独立开发者越来越多了?
不知道你有没有观察到,从2023年开始,国内的独立开发者越来越多了。 之前独立开发者是一个非常小众的群体,但现在很多互联网从业者都瞄准了这个方向,包括程序员、产品经理,运营等等。 我想可能是这样几个原因…...

GPT4不限制使用次数了!GPT5即将推出了!
今天登录到ChatGPT Plus账户,出现了如下提示: 已经没有了数量和时间限制的提示。 更改前:每 3 小时限制 40 次(团队计划为 100 次);更改后:可能会应用使用限制。 GPT-4放开限制 身边订阅了Ch…...

物联网实战--入门篇之(六)嵌入式-WIFI驱动(ESP8266)
目录 一、WIFI简介 二、基础网络知识 三、思路讲解 四、代码分析 4.1 状态机制 4.2 客户端连接 4.3 应用数据接收处理 4.4 数据发送 4.5 主函数调用 4.6 网络连接ID分配 五、总结 一、WIFI简介 WIFI在我们生活中太常见了,手机电脑都可以用WiFi连接路由器进行上…...

Java并发编程基础面试题详细总结
1. 什么是线程和进程? 1.1 何为进程? 进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的。系统运行一个程序即是一个进程从创建,运行到消亡的过程。 在 Java 中,当我们启动 main 函数时其实就是启动了一个…...

EKO / 砍树
暴力是不行的,还得是二分吧 题目描述 伐木工人 Mirko 需要砍 M 米长的木材。对 Mirko 来说这是很简单的工作,因为他有一个漂亮的新伐木机,可以如野火一般砍伐森林。不过,Mirko 只被允许砍伐一排树。 Mirko 的伐木机工作流程如下&a…...

Kafka面试宝典
1 Kafka基础面试篇 Kafka的那些设计让它有如此高的性能? 1.partition,producer和consumer端的批处理:提高并行度;2.页缓存:大量使用页缓存,内存操作比磁盘操作快很多,数据写入直接写道页缓存,由操作系统负责刷盘,数据读取也是直接命中页缓存,从内存中直接拿到数据;…...

Redis性能管理
目录 1、内存碎片如何产生的? 2、跟踪内存碎片率对理解Redis实例的资源性能是非常重要的 3、解决碎片率大的问题 二、内存使用率 1、避免内存交换发生的方法 2、内回收key 三、缓存的穿透、击穿、雪崩 #查看Redis内存使用方法 info memory #进入数据库查看 re…...

计算机网络:局域网的数据链路层
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

Linux常见命令简介
Linux运行级别 六种运行级别: 0、关机 1、单用户(可用来找回密码) 2、多用户无网络 3、多用户有网络(多用于工作环境) 4、预留 5、图形界面(多用于学习环境) 6、重…...
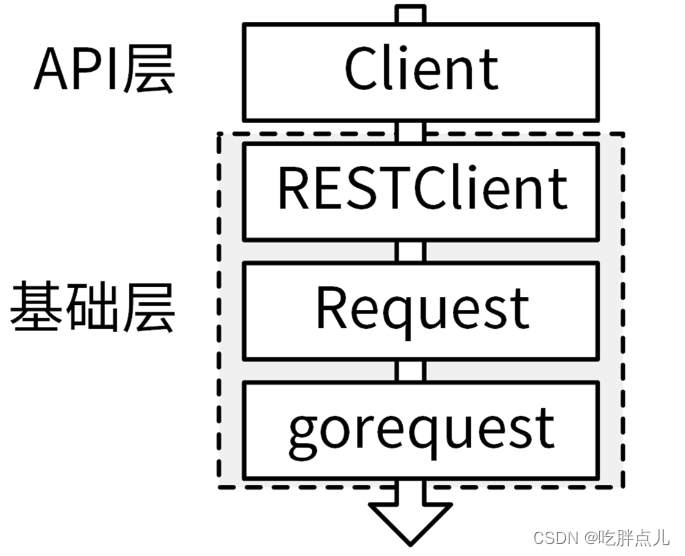
34-SDK设计(下):IAM项目GoSDK设计和实现
比如 Kubernetes的 client-go SDK设计方式。IAM项目参考client-go,也实现了client-go风格的SDK:marmotedu-sdk-go。 ,client-go风格的SDK具有以下优点: 大量使用了Go interface特性,将接口的定义和实现解耦࿰…...
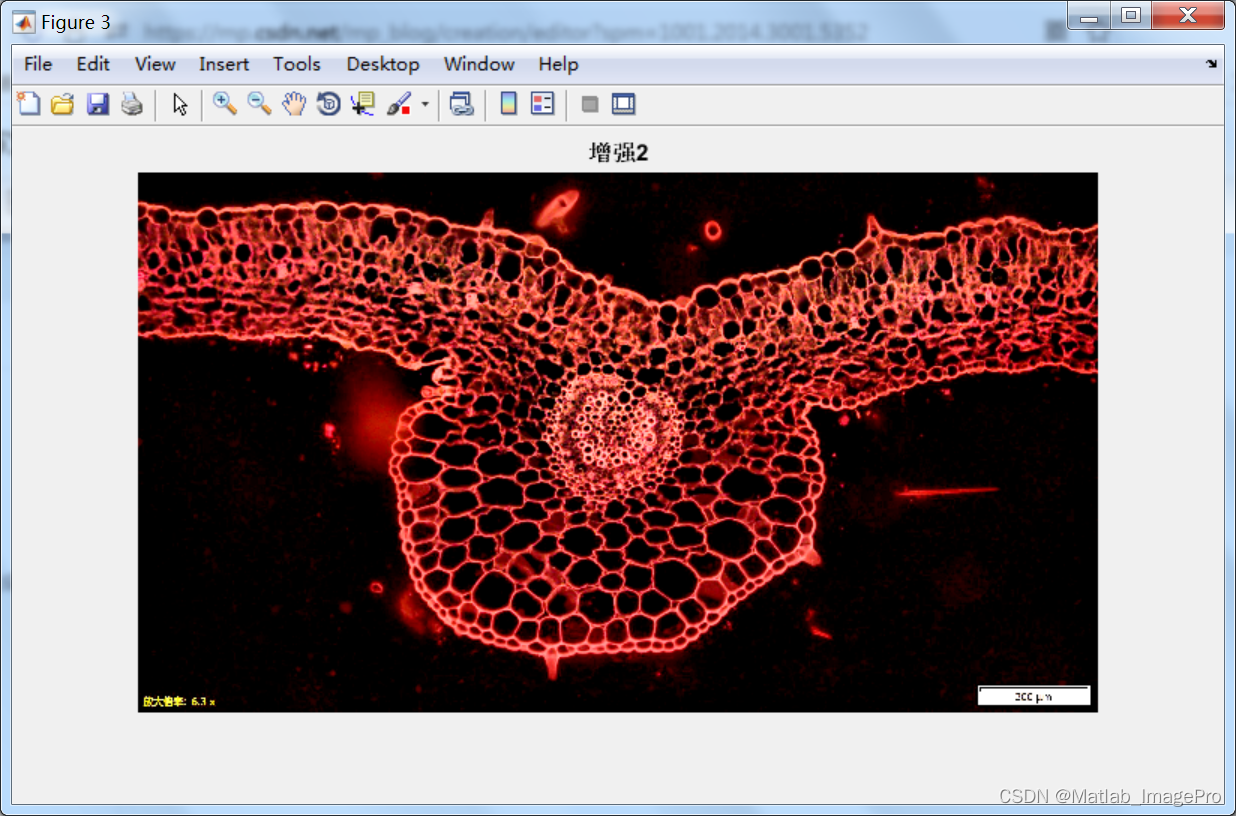
基于Matlab的血管图像增强算法,Matlab实现
博主简介: 专注、专一于Matlab图像处理学习、交流,matlab图像代码代做/项目合作可以联系(QQ:3249726188) 个人主页:Matlab_ImagePro-CSDN博客 原则:代码均由本人编写完成,非中介,提供…...

LeetCode每日一题之专题一:双指针 ——复写零
复写零OJ链接:1089. 复写零 - 力扣(LeetCode) 题目: 解法(原地复写-双指针): 算法思路: 如果「从前向后」进⾏原地复写操作的话,由于 0 的出现会复写两次,导致…...

Golang基础-9
Go语言基础 介绍 基础 结构体 自定义类型 结构体定义 结构体声明 结构体初始化 字段访问与修改 匿名结构体 结构体嵌套 初始化函数定义 介绍 本文介绍Go语言中自定义类型、结构体定义、结构体声明、结构体初始化、字段访问与修改、匿名结构体、结构体嵌套、初始化…...
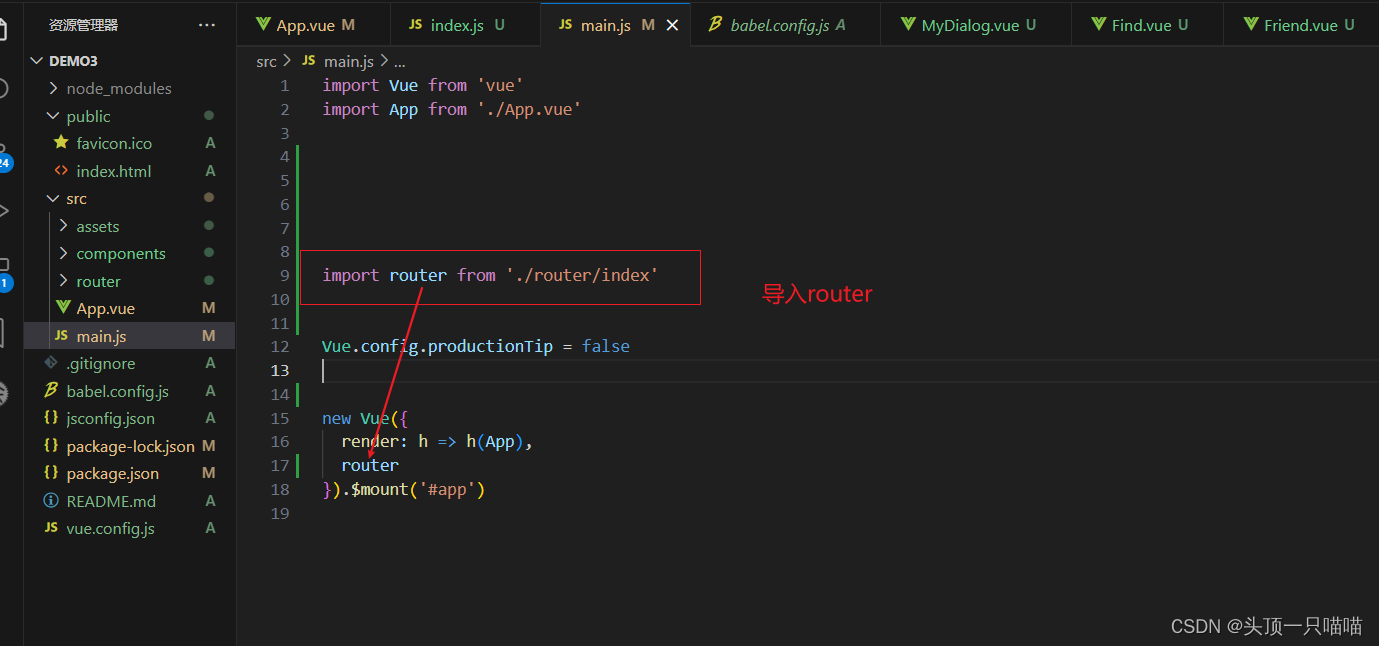
Vue基础知识:路由的封装抽离,路由模块的封装抽离的好处是什么?,如何快速的引入组件,基于@指代src目录,从src目录出发找组件
如果将所有的路由配置都存放在main.js中,是非常有问题的,杂且乱。所以我们要将路由模块进行抽离,这样有利于:拆分模块,利于维护。大致的做法就是将路由相关的东西放到router这个文件夹的index.js中,而将来只…...

插入排序---算法
1、算法概念 插入排序:它的工作原理是通过构建有序排序,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置插入。 2、算法步骤 将第一待排序序列第一个元素看作一个有序序列,把第二个元素到最后一个元素当成是…...

Vue3 Vite 整合组件脚手架笔记
序号更新时间备注12024.04.03初始化整理笔记 目录 一、安装运行命令二、相关依赖内容 1、http客户端 - alova2、国际化 - I18n3、时间管理 - moment4、pdf预览 - pdfjs-dist5、doc预览 - docx-preview6、请求参数处理 - qs7、全局状态管理 - Pinia8、路由管理 - vue-router9、…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
