【独立开发前线】Vol.36 为什么从2023年开始,独立开发者越来越多了?
不知道你有没有观察到,从2023年开始,国内的独立开发者越来越多了。
之前独立开发者是一个非常小众的群体,但现在很多互联网从业者都瞄准了这个方向,包括程序员、产品经理,运营等等。
我想可能是这样几个原因:
1.公司和个体之间的关系已经不像是过去那样,个体必须要依附于公司,而是可以平等对话。比如像超级主播李佳琦、董宇辉、薇娅,他们一个人的业绩就能顶得上一家上市公司。而独立开发者也是一样,一个人做出的产品,其收入就可以超过其上班的工资回报。
在这种情况下,上班的意义就不大了。努力提升产品收入,用独立开发产品来养活自己显然是更好的选择。可以充满发挥创意,有足够的掌控感跟自由度。不用担心35岁被裁员的问题。
2.目前的机遇很好,GPT的出现,AI的大规模爆发。让独立开发者一人可以做出成熟度非常高的作品。即使只有一人团队,也可以完成包括编程、推广、运营、UI等工作。有了AI的协助,工作效率大幅提升,可以快速搭建小产品。
另外一点就是现在产品变现的方式非常多样化,只要你的产品可以服务一小波人,一个垂直群体,就可以进行变现。可以通过虚拟权益、会员、卖课、付费社群、知识星球、小报童、竹白NewsLetter、爱发电、创作者收益、甚至微信转账等等。变现的方式非常多样化,只要你能够搭建出产品,真正为他人解决了一个问题,那么很容易变现。
不用依赖10年前的商业模式,免费产品服务,通过广告来变现。今天的独立开发者可以服务好一小波人,让他们直接付费给你。哪怕只有1000个付费用户,每人1年100元,也可以收获10万的ARR。如果通过广告变现的话,可能不到1000块。
为什么会这样呢?因为我们已经过了那个免费的就是最好的时代,在今天的互联网,用户是会愿意为了好的产品付费的。市场被大厂的各种产品轮番教育,用户已经有了付费意识,很多割韭菜的知识星球都可以卖出去上千万。所以只要你的产品是值得的,就会有人愿意付费给你。
3.目前的市场环境,现在工作不好找,升职加薪越来越难。好的坑位就那么多,如果在职场上难以上升。那么成为独立开发者不失为一个好的选择。至少在天气很冷的时候,你可以窝在沙发里写代码,煮一杯热气腾腾的咖啡,一边创作一边赚钱。
另外,即使你的独立开发作品赚不了大钱,即使1年只有10个付费用户,那也是对你的认可,也可以为你创造被动收入。这些事情会让你充满成就感,看到微信收款进账可比刷抖音快乐多了。
4.独立开发可以远程办公,可以在家,也可以在星巴克。可以在北上广深,也可以去大理洱海,当你的产品运行稳定后,你有了更大的自由度。可以将生活跟工作平衡一下。在上班的时候,可能每天回到家已经筋疲力尽了。无暇顾及家人和生活,但如果独立产品营收稳定,你可以更好的平衡自己的时间,让生活更加丰富多彩。
打工不过是拿每天8小时的工作去交换每个人的固定薪酬,按公司的规则去做事。而独立开发则是用自己的产品价值去交换用户的付费,按自己的规则去做事。
如果你习惯在既定的规则下行事,需要别人给你发号施令,那么你不适合独立开发。
如果你自驱力非常强,即使没有人催你,你也会把自己的热情投入到产品上,相信我,你一定能成,无非是多试几次罢了。
最后,如果你想了解更多的独立开发idea,认识更多独立开发者,欢迎加入独立开发社群,与更多同路人一同前行!
订阅:独立开发前线:独立开发者的成长指南!
网站:https://www.91wink.com
如果你想加入独立开发交流群,欢迎加我V:Ovelv2023
相关文章:

【独立开发前线】Vol.36 为什么从2023年开始,独立开发者越来越多了?
不知道你有没有观察到,从2023年开始,国内的独立开发者越来越多了。 之前独立开发者是一个非常小众的群体,但现在很多互联网从业者都瞄准了这个方向,包括程序员、产品经理,运营等等。 我想可能是这样几个原因…...

GPT4不限制使用次数了!GPT5即将推出了!
今天登录到ChatGPT Plus账户,出现了如下提示: 已经没有了数量和时间限制的提示。 更改前:每 3 小时限制 40 次(团队计划为 100 次);更改后:可能会应用使用限制。 GPT-4放开限制 身边订阅了Ch…...

物联网实战--入门篇之(六)嵌入式-WIFI驱动(ESP8266)
目录 一、WIFI简介 二、基础网络知识 三、思路讲解 四、代码分析 4.1 状态机制 4.2 客户端连接 4.3 应用数据接收处理 4.4 数据发送 4.5 主函数调用 4.6 网络连接ID分配 五、总结 一、WIFI简介 WIFI在我们生活中太常见了,手机电脑都可以用WiFi连接路由器进行上…...

Java并发编程基础面试题详细总结
1. 什么是线程和进程? 1.1 何为进程? 进程是程序的一次执行过程,是系统运行程序的基本单位,因此进程是动态的。系统运行一个程序即是一个进程从创建,运行到消亡的过程。 在 Java 中,当我们启动 main 函数时其实就是启动了一个…...

EKO / 砍树
暴力是不行的,还得是二分吧 题目描述 伐木工人 Mirko 需要砍 M 米长的木材。对 Mirko 来说这是很简单的工作,因为他有一个漂亮的新伐木机,可以如野火一般砍伐森林。不过,Mirko 只被允许砍伐一排树。 Mirko 的伐木机工作流程如下&a…...

Kafka面试宝典
1 Kafka基础面试篇 Kafka的那些设计让它有如此高的性能? 1.partition,producer和consumer端的批处理:提高并行度;2.页缓存:大量使用页缓存,内存操作比磁盘操作快很多,数据写入直接写道页缓存,由操作系统负责刷盘,数据读取也是直接命中页缓存,从内存中直接拿到数据;…...

Redis性能管理
目录 1、内存碎片如何产生的? 2、跟踪内存碎片率对理解Redis实例的资源性能是非常重要的 3、解决碎片率大的问题 二、内存使用率 1、避免内存交换发生的方法 2、内回收key 三、缓存的穿透、击穿、雪崩 #查看Redis内存使用方法 info memory #进入数据库查看 re…...

计算机网络:局域网的数据链路层
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

Linux常见命令简介
Linux运行级别 六种运行级别: 0、关机 1、单用户(可用来找回密码) 2、多用户无网络 3、多用户有网络(多用于工作环境) 4、预留 5、图形界面(多用于学习环境) 6、重…...
34-SDK设计(下):IAM项目GoSDK设计和实现
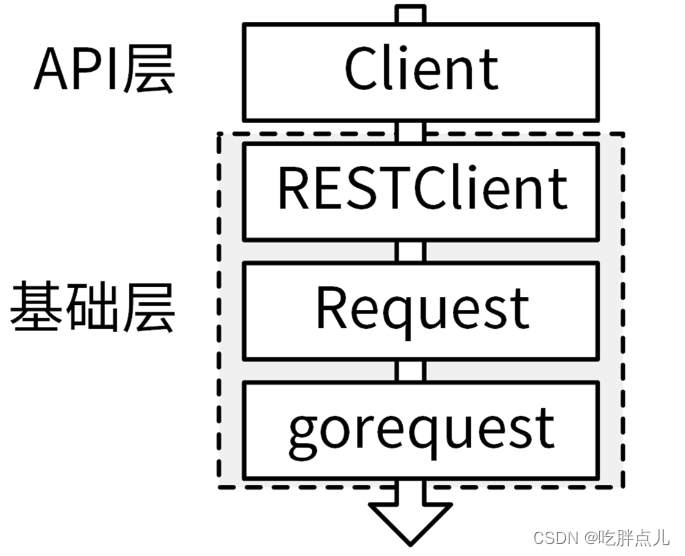
比如 Kubernetes的 client-go SDK设计方式。IAM项目参考client-go,也实现了client-go风格的SDK:marmotedu-sdk-go。 ,client-go风格的SDK具有以下优点: 大量使用了Go interface特性,将接口的定义和实现解耦࿰…...
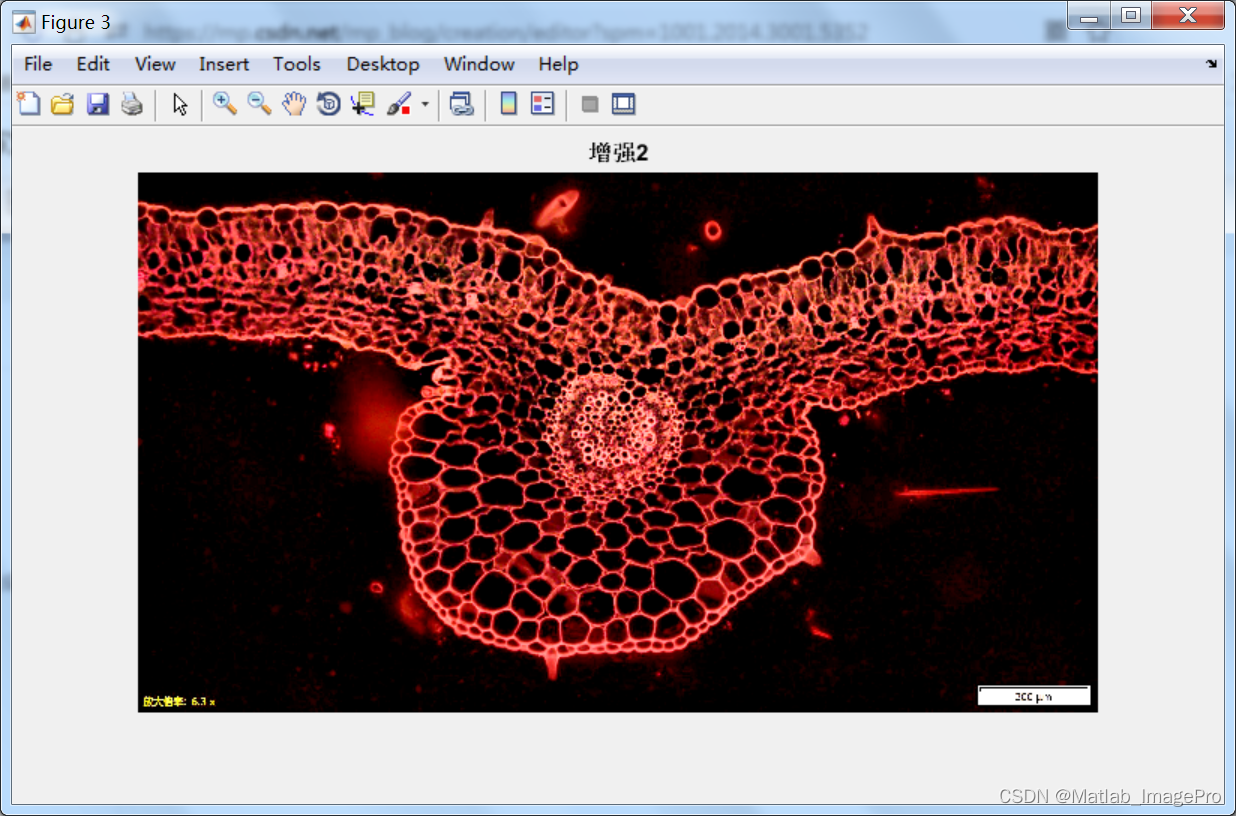
基于Matlab的血管图像增强算法,Matlab实现
博主简介: 专注、专一于Matlab图像处理学习、交流,matlab图像代码代做/项目合作可以联系(QQ:3249726188) 个人主页:Matlab_ImagePro-CSDN博客 原则:代码均由本人编写完成,非中介,提供…...

LeetCode每日一题之专题一:双指针 ——复写零
复写零OJ链接:1089. 复写零 - 力扣(LeetCode) 题目: 解法(原地复写-双指针): 算法思路: 如果「从前向后」进⾏原地复写操作的话,由于 0 的出现会复写两次,导致…...

Golang基础-9
Go语言基础 介绍 基础 结构体 自定义类型 结构体定义 结构体声明 结构体初始化 字段访问与修改 匿名结构体 结构体嵌套 初始化函数定义 介绍 本文介绍Go语言中自定义类型、结构体定义、结构体声明、结构体初始化、字段访问与修改、匿名结构体、结构体嵌套、初始化…...
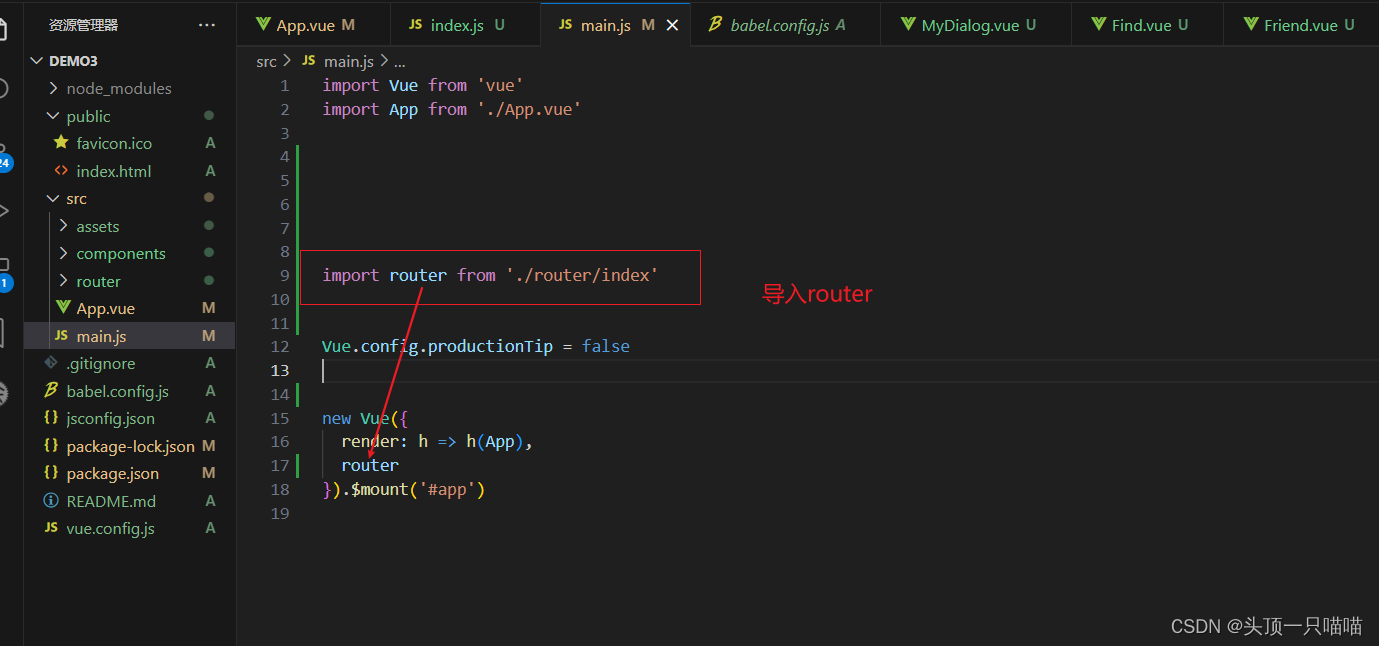
Vue基础知识:路由的封装抽离,路由模块的封装抽离的好处是什么?,如何快速的引入组件,基于@指代src目录,从src目录出发找组件
如果将所有的路由配置都存放在main.js中,是非常有问题的,杂且乱。所以我们要将路由模块进行抽离,这样有利于:拆分模块,利于维护。大致的做法就是将路由相关的东西放到router这个文件夹的index.js中,而将来只…...

插入排序---算法
1、算法概念 插入排序:它的工作原理是通过构建有序排序,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置插入。 2、算法步骤 将第一待排序序列第一个元素看作一个有序序列,把第二个元素到最后一个元素当成是…...

Vue3 Vite 整合组件脚手架笔记
序号更新时间备注12024.04.03初始化整理笔记 目录 一、安装运行命令二、相关依赖内容 1、http客户端 - alova2、国际化 - I18n3、时间管理 - moment4、pdf预览 - pdfjs-dist5、doc预览 - docx-preview6、请求参数处理 - qs7、全局状态管理 - Pinia8、路由管理 - vue-router9、…...

续二叉搜索树递归玩法
文章目录 一、插入递归二、寻找递归(非常简单,走流程就行)三、插入递归(理解起来比较麻烦) 先赞后看,养成习惯!!!^ _ ^<3 ❤️ ❤️ ❤️ 码字不易,大家的…...

DDD 的四层领域模型是怎样的?包含哪些基础概念?
DDD的四层领域模型如下所示: 展现层:这一层负责向用户显示信息和解释用户命令,完成前端界面逻辑。并将用户请求传递给应用层。应用层:这一层是很薄的一层,负责协调领域层中的领域对象,组成具体应用场景。应…...

AI 在医疗保健领域的应用:技术、趋势和前景
人工智能(AI)在医疗保健领域的应用已经成为引人瞩目的发展方向,其在医学影像分析、疾病诊断和个性化治疗等方面展现出了巨大潜力。本文将深入探讨这些技术应用和未来的发展趋势。 医学影像分析 医学影像分析是AI在医疗领域中应用最广泛的领…...

SVG XML 格式定义图形入门介绍
SVG SVG means Scalable Vector Graphics. SVG 使用 XML 格式定义图形SVG 图像在放大或改变尺寸的情况下其图形质量不会有所损失SVG 是万维网联盟的标准 Hello World Use SVG in html and you can see: Link to the SVG file You can use <a> tag to link to the svg…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
