当前位置：首页 > news >正文

【拓扑空间】示例及详解1

news 2026/2/8 18:48:50

例1

度量空间 $(X,d)$ 的任意两球形邻域的交集是若干球形邻域的并集

Proof：

任取空间 $(X,d)$ 的两个球形邻域 $B(x_1,\varepsilon _1)$ 、 $B(x_2,\varepsilon _2)$ ，令 $U=B(x_1,\varepsilon _1)\cap B(x_2,\varepsilon _2)$

任取 $x\in U$ ,令 $\varepsilon_x=min\left \{ \varepsilon_1-d(x_1,x), \varepsilon_2-d(x_2,x) \right \}$

$\Rightarrow B(x,\varepsilon_x)\subseteq U$

$\Rightarrow U=\bigcup_{x\in U}B(x,\varepsilon_x)$

球形领域 $B(x_0,\varepsilon )=\left \{ x \in X : d(x,x_0)< \varepsilon,x_0\in X,\varepsilon >0 \right \}$

例2

规定X的子集族 $\tau_d=\left \{ U:U\ is \ union \ of\ spherical \ neighborhoods \right \}$ ,证明 $\tau_d$ 是X上的一个拓扑

Proof：

1. $\varnothing \in \tau_d$

$X=\bigcup_{x\in X}B(x,\varepsilon_x) \in \tau_d$

2. $\forall u_1,u_2 \in \tau_d, u_1\cup u_2 \ is \ union\ of\ spherical\ neighboorhoods$ , $u_1\cup u_2\in\tau_d$

（若干个球形邻域的并集都是 $\tau_d$ 的元素，元素间的任意并依旧是若干个球形邻域的并集，故对任意并封闭）

3. $\begin{gathered}\exists u_1,u_2\in\tau_d,u_1=\bigcup_{\alpha }B(x_{\alpha},\varepsilon_{\alpha}),u_2=\bigcup_{\beta}B(x_{\beta},\varepsilon_{\beta}).\end{gathered}$

$\begin{gathered} u_1\cap u_2=\left(\bigcup_\alpha B(x_\alpha,\varepsilon_\alpha)\right)\bigcap\left(\bigcup_\beta B(x_\beta,\varepsilon_\beta)\right) \\ =\bigcup_{\alpha,\beta}\left(B(x_{a},\varepsilon_{a})\bigcap B(x_{\beta},\varepsilon_{\beta})\right) \end{gathered}$

$let \ U =B(x_{a},\varepsilon_{a})\bigcap B(x_{\beta},\varepsilon_{\beta})$

$\forall x \in U,let \ \varepsilon_x=min\left \{ d(x,x_\alpha),d(x,x_\beta) \right \}$

$then,U=\bigcup_{x\in U}B(x,\varepsilon_x)$

$\begin{gathered} then,u_1\cap u_2=\bigcup_{\alpha,\beta}\left(\bigcup_{x\in U}B(x,\varepsilon_x)\right) \end{gathered},so \ u_1\cap u_2 \in \tau_d$

$therefore \ \tau_d \ is \ a \ topo \ in\ X$

拓扑：=

1. $X,\varnothing \in \tau$

2.任意并封闭

3.有限交封闭

$\left(\bigcup_\alpha B(x_\alpha,\varepsilon_\alpha)\right)\bigcap\left(\bigcup_\beta B(x_\beta,\varepsilon_\beta)\right) =\bigcup_{\alpha,\beta}\left(B(x_{a},\varepsilon_{a})\bigcap B(x_{\beta},\varepsilon_{\beta})\right)$

一般称 $\tau_d$ 为X上由度量d决定的度量拓扑

每个度量空间都可以看成具有度量拓扑的拓扑空间，从而欧氏空间 $E^{n}$ 也是拓扑空间，其度量拓扑称为欧氏拓扑。

从这个意义上讲，拓扑空间是欧氏空间和度量空间的推广，拓扑公理也是从度量空间的开集的基本性质中抽象出来的。

【拓扑空间】示例及详解1

例1 度量空间的任意两球形邻域的交集是若干球形邻域的并集 Proof： 任取空间的两个球形邻域、，令任取,令球形领域例2 规定X的子集族,证明是X上的一个拓扑 Proof： 1. 2., （若干个球形邻域的并集都是的元素，元素…...

编程日记 2024/4/5 20:24:31

linux安装jdk8

上传到某个目录，例如：/usr/local/ tar -xvf jdk-8u144-linux-x64.tar.gz配置环境变量： export JAVA_HOME/usr/local/java export PATH$PATH:$JAVA_HOME/bin设置环境变量： source /etc/profile...

编程日记 2024/4/5 20:23:30

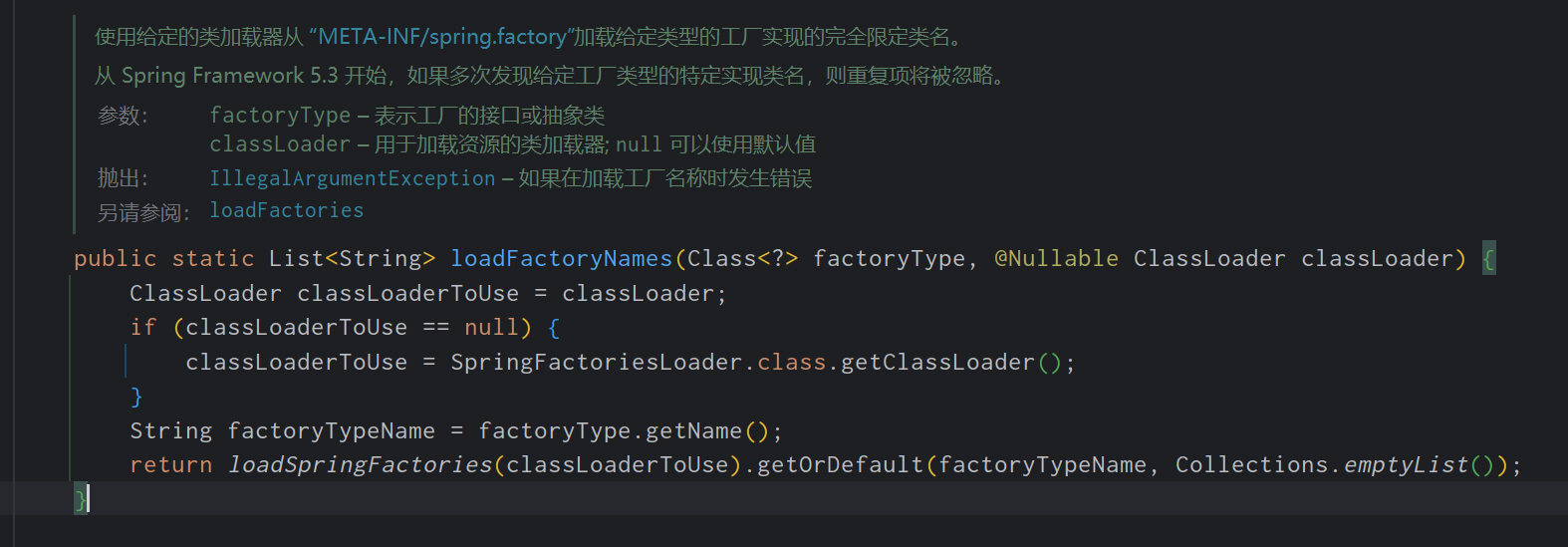
Spring重点知识（个人整理笔记）

目录 1. 为什么要使用 spring？ 2. 解释一下什么是 Aop？ 3. AOP有哪些实现方式？ 4. Spring AOP的实现原理 5. JDK动态代理和CGLIB动态代理的区别？ 6. 解释一下什么是 ioc？ 7. spring 有哪些主要模块？…...

编程日记 2024/4/5 20:21:29

HTML基础知识详解（上）（如何想知道html的全部基础知识点，那么只看这一篇就足够了！）

前言：在学习前端基础时，必不可少的就是三大件（html、css、javascript ），而HTML（超文本标记语言——HyperText Markup Language）是构成 Web 世界的一砖一瓦，它定义了网页内容的含义和…...

编程日记 2024/4/5 20:18:26

如何借助Idea创建多模块的SpringBoot项目

目录 1.1、前言1.2、开发环境1.3、项目多模块结构1.4、新建父工程1.5、创建子模块1.6、编辑父工程的pom.xml文件 1.1、前言 springmvc项目，一般会把项目分成多个包:controler、service、dao、utl等，但是随着项目的复杂性提高，想复用其他一个模…...

编程日记 2024/4/5 20:16:24

爬虫新闻网站并存储到CSV文件以红网为例 V1.0

爬虫：红网网站， 获取当月指定关键词新闻，并存储到CSV文件 V1.0 目标网站：红网爬取目的：为了获取某一地区更全面的在红网已发布的宣传新闻稿，同时也让自己的工作更便捷环境：Pycharm2021&#…...

编程日记 2024/4/5 20:12:21

CentOS 使用 Cronie 实现定时任务

CentOS 使用 Cronie 实现定时任务文章目录 CentOS 使用 Cronie 实现定时任务一、简介二、基本使用1、常用命令2、使用示例第一步：创建脚本/home/create.sh第二步：添加定时任务第三步：重启 cronie 服务额外：查看 cronie 运行状态定…...

编程日记 2024/4/5 20:07:16

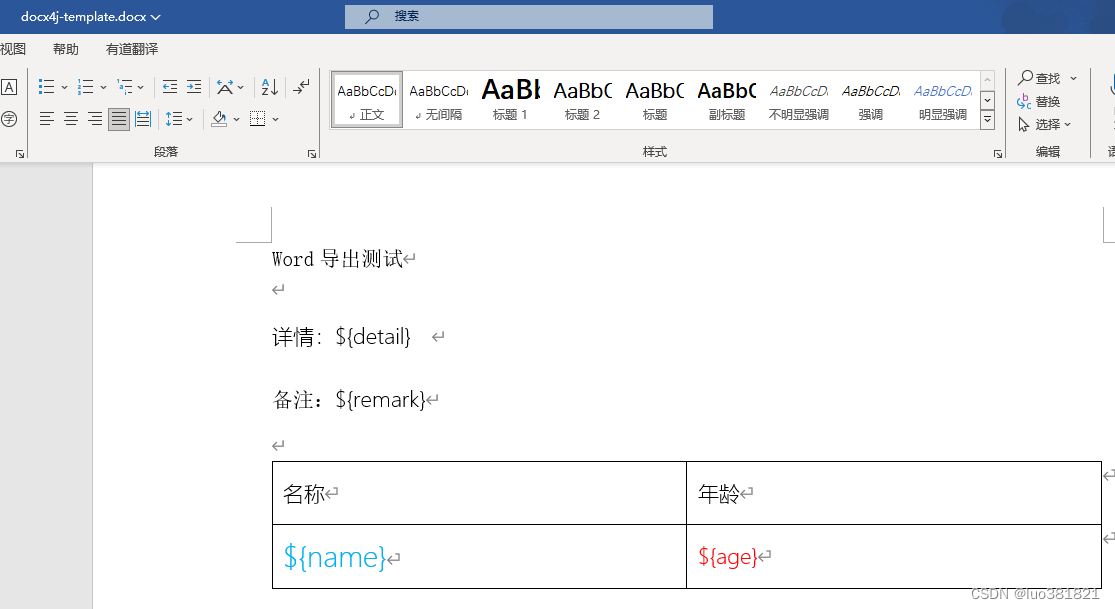
java生成word

两种方案一、poi-tl生成word <dependency><groupId>com.deepoove</groupId><artifactId>poi-tl</artifactId><version>1.12.1</version> </dependency> public static void main(String[] args) throws Exception {String…...

编程日记 2024/4/5 20:06:14

C语言中的结构体：揭秘数据的魔法盒

前言在C语言的广阔天地中，结构体无疑是一颗璀璨的明珠。它就像是一个魔法盒，能够容纳各种不同类型的数据，并按我们的意愿进行组合和排列。那么，这个魔法盒究竟有何神奇之处呢？让我们一探究竟。一、结构体的诞生&…...

编程日记 2024/4/5 20:04:11

Listener

文章目录 ListenerServletContextListenerServletContextAttributeListenerHttpSessionListenerHttpSessionAttributeListenerServletRequestListenerServletRequestAttributeListenerHttpSessionBindingListenerHttpSessionActivationListener Listener Listener 监听器它是 J…...

编程日记 2024/4/5 20:01:08

单细胞RNA测序（scRNA-seq）SRA数据下载及fastq-dumq数据拆分

单细胞RNA测序（scRNA-seq）入门可查看以下文章： 单细胞RNA测序（scRNA-seq）工作流程入门单细胞RNA测序（scRNA-seq）细胞分离与扩增 1. NCBI查询scRNA-seq SRA数据 NCBI地址： https…...

编程日记 2024/4/5 19:59:06

金蝶Apusic应用服务器未授权目录遍历漏洞复现

0x01 产品简介金蝶Apusic应用服务器（Apusic Application Server，AAS）是一款标准、安全、高效、集成并具丰富功能的企业级应用服务器软件，全面支持JakartaEE8/9的技术规范，提供满足该规范的Web容器、EJB容器以及WebService容器等，支持Websocket1.1、Servlet4.0、HTTP2.0…...

编程日记 2024/4/5 19:57:04

成都百洲文化传媒有限公司电商服务的新领军者

在当今数字化时代，电商行业正以前所未有的速度蓬勃发展。在这个大背景下，成都百洲文化传媒有限公司凭借其深厚的行业经验和精湛的专业技能，正迅速崛起为电商服务领域的新领军者。一、专业引领，成就卓越作为一家专注于电商服务的…...

编程日记 2024/4/5 19:51:59

从无到有开始创建动态顺序表——C语言实现

顺序表的概念顺序表的底层结构是数组，对数组的封装，实现了常用的增删改查等接口。在物理结构和逻辑结构都是连续的，物理结构是指顺序表在计算机内存的存储方式，逻辑结构是我们思考的形式，顺序表和数组是类似的&#x…...

编程日记 2024/4/5 19:50:58

Unix 网络编程, Socket 以及bind（）, listen（）, accept（）, connect（）, read（）write（）五大函数简介

Unix网络编程是针对类Unix操作系统（包括Linux、BSD以及其他遵循POSIX标准的操作系统）进行网络通信开发的技术领域。网络编程涉及创建和管理网络连接、交换数据以及处理不同层次网络协议栈上的各种网络事件。在Unix环境中，网络编程通常涉及到以…...

编程日记 2024/4/5 19:49:57

【附下载】2024全行业数字化转型企业建设解决方案PPT合集

精品推荐，2024全行业数字化转型企业建设解决方案PPT合集，精品PPT源格式共21份。以下是资料目录，如需下载，请前往星球获取： 1.制造业数字化转型解决方案及应用.pptx 2.医院数字化网络解决方案.pptx 3.食品饮料工厂数字…...

编程日记 2024/4/5 19:48:56

【QT+QGIS跨平台编译】056：【pdal_lepcc+Qt跨平台编译】（一套代码、一套框架，跨平台编译）

点击查看专栏目录文章目录一、pdal_lepcc介绍二、pdal下载三、文件分析四、pro文件五、编译实践一、pdal_lepcc介绍 pdal_lepcc 是 PDAL（Point Data Abstraction Library）的一个插件，用于点云数据的压缩。它基于 EPCC（Entwine Point Cloud Compression）算法，提供了对点…...

编程日记 2024/4/5 19:47:55

蓝桥集训之斐波那契数列

蓝桥集训之斐波那契数列核心思想：矩阵乘法将原本O(n)的递推算法优化为O(log2n) 构造1x2矩阵f和2x2矩阵a 发现f(n1) f(n) * a 则f(n1) f(1) * an可以用快速幂优化 #include <iostream>#include <cstring>#include <algorithm>using na…...

编程日记 2024/4/5 19:43:51

程序员的工资是多少，和曹操有莫大的关系

曹操是谁大家都知道了吧，他是三国时期的一个有名的大老板，谁知道曹操的工资是多少呢？这个其实也不好说，有时候曹操赚很多的钱，有时候也亏血本，甚至连脑袋都差点掉了。创业不容易啊，曹老板也是如…...

编程日记 2024/4/5 19:42:50

使用Element Plus

1. 官网安装安装 | Element Plus (gitee.io) 安装： npm install element-plus --save 在main.ts中全局注册ElementPlus并使用 //加入element-plus import ElementPlus from element-plus; //加入element-plus样式 import element-plus/dist/index.css; import…...

编程日记 2024/4/5 19:41:49

接口测试中缓存处理策略

在接口测试中，缓存处理策略是一个关键环节，直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性，避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明： 一、缓存处理的核…...

编程新知 2026/2/8 4:37:27

pam_env.so模块配置解析

在PAM（Pluggable Authentication Modules）配置中， /etc/pam.d/su 文件相关配置含义如下： 配置解析 auth required pam_env.so1. 字段分解字段值说明模块类型auth认证类模块，负责验证用户身份&am…...

编程新知 2025/10/5 8:09:39

数据链路层的主要功能是什么

数据链路层（OSI模型第2层）的核心功能是在相邻网络节点（如交换机、主机）间提供可靠的数据帧传输服务，主要职责包括： 🔑 核心功能详解： 帧封装与解封装封装： 将网络层下发…...

编程新知 2026/2/1 7:31:51

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据案例一对于查询类API，查询的是单条数据，比如根据主键ID查询用户信息，sql如下： select id, name, age from user where id #{id}API默认返回的数据格式是多条的，如下： {&qu…...

编程新知 2026/2/2 22:06:13

是否存在路径（FIFOBB算法）

题目描述一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。输入第一行两个整数，分别表示n 和 e 的值（1…...

编程新知 2025/10/1 6:09:21

热烈祝贺埃文科技正式加入可信数据空间发展联盟

2025年4月29日，在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上，可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞，强调该联盟是推进全国一体化数据市场建设的关键抓手。郑州埃文科技有限公司&am…...

编程新知 2026/2/7 20:23:55

《信号与系统》第 6 章信号与系统的时域和频域特性

目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

编程新知 2026/2/5 4:45:50

第2课 SiC MOSFET与 Si IGBT 静态特性对比

2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比器件的输出特性描述了当温度和栅源电压（栅射电压）为某一具体数值时，漏极电流(集电极电流...

编程新知 2026/1/27 0:16:47

Gitlab + Jenkins 实现 CICD

CICD 是持续集成（Continuous Integration, CI）和持续交付/部署（Continuous Delivery/Deployment, CD）的缩写，是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后，自动发布…...

编程新知 2026/1/28 1:10:54

Redis专题-实战篇一-基于Session和Redis实现登录业务

GitHub项目地址：https://github.com/whltaoin/redisLearningProject_hm-dianping 基于Session实现登录业务功能提交版本码：e34399f 基于Redis实现登录业务提交版本码：60bf740 一、导入黑马点评后端项目项目架构图 1. 前期阶段2. 后续阶段导…...

编程新知 2026/1/29 16:45:50

例1

例2

相关文章：