蓝桥集训之斐波那契数列
蓝桥集训之斐波那契数列
-
核心思想:矩阵乘法
-
将原本O(n)的递推算法优化为O(log2n)
-

-
构造1x2矩阵f和2x2矩阵a
-
发现f(n+1) = f(n) * a
- 则f(n+1) = f(1) * an
- 可以用快速幂优化
-
-
#include <iostream>#include <cstring>#include <algorithm>using namespace std;const int MOD = 10000;int f[2];int a[2][2];int n;void mul1(){int res[2]; //res = res*a 求1x2矩阵memset(res,0,sizeof res);for(int i=0;i<2;i++)for(int j=0;j<2;j++)res[i] = (res[i] + f[j] * a[j][i]) %MOD; //计算f*amemcpy(f,res,sizeof f);}void mul2(){int res[2][2]; //a = a*a 求2x2矩阵memset(res,0,sizeof res);for(int i=0;i<2;i++)for(int j=0;j<2;j++)for(int k=0;k<2;k++)res[i][j] = (res[i][j] + a[i][k] * a[k][j])%MOD; //计算a*amemcpy(a,res,sizeof a);}void qmi(int n){while (n) //快速幂优化{ if(n&1) mul1(); //res = res*a%MODmul2(); //a = a*a%MODn>>=1;}}int main(){while(cin>>n , n!=-1){f[0] = 0,f[1] = 1; //初始化第0 1项a[0][0] = 0,a[0][1] = 1,a[1][0] = 1,a[1][1] = 1; //初始化a矩阵qmi(n); cout<<f[0]<<endl;}return 0;}
相关文章:

蓝桥集训之斐波那契数列
蓝桥集训之斐波那契数列 核心思想:矩阵乘法 将原本O(n)的递推算法优化为O(log2n) 构造1x2矩阵f和2x2矩阵a 发现f(n1) f(n) * a 则f(n1) f(1) * an可以用快速幂优化 #include <iostream>#include <cstring>#include <algorithm>using na…...

程序员的工资是多少,和曹操有莫大的关系
曹操是谁大家都知道了吧,他是三国时期的一个有名的大老板,谁知道曹操的工资是多少呢?这个其实也不好说,有时候曹操赚很多的钱,有时候也亏血本,甚至连脑袋都差点掉了。创业不容易啊,曹老板也是如…...

使用Element Plus
1. 官网安装 安装 | Element Plus (gitee.io) 安装: npm install element-plus --save 在main.ts中全局注册ElementPlus并使用 //加入element-plus import ElementPlus from element-plus; //加入element-plus样式 import element-plus/dist/index.css; import…...
设计模式总结)
单例(Singleton)设计模式总结
1. 设计模式概述: 设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、以及解决问题的思考方式。设计模式免去我们自己再思考和摸索。 就像是经典的棋谱,不同的棋局,我们用不同的棋谱。"套路"经典的设计模式一共有…...

LeetCode每日一题之专题一:双指针 ——快乐数
快乐数OJ链接:202. 快乐数 - 力扣(LeetCode) 题目: 题目分析: 为了房便叙述,将「对于⼀个正整数,每⼀次将该数替换为它每个位置上的数字的平方和」这⼀个 操作记为 x 操作; 题目告诉我们&#…...
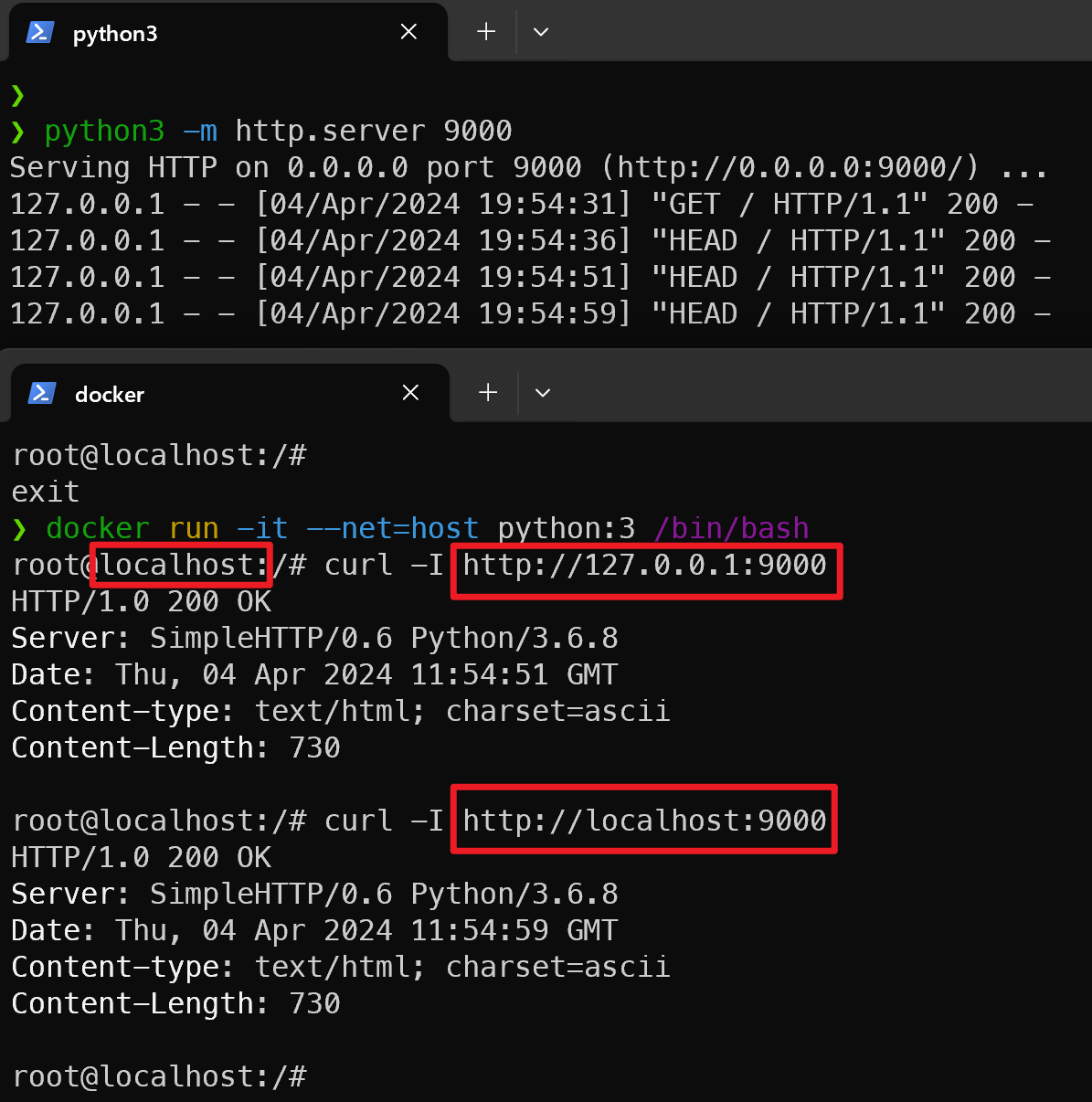
Docker Desktop 不支持 host 网络模式
先把这个结论的放在前面,直接访问链接就能看到官方文档中已经明确说了不支持。 参考链接:docker desktop for windows 不支持 host 网络模式 以前对于 docker 的网络模式,一直只是了解,没有亲自尝试过。结果今天在尝试 docker 的 …...

Linux网络编程二(TCP图解三次握手及四次挥手、TCP滑动窗口、MSS、TCP状态转换、多进程/多线程服务器实现)
文章目录 1、TCP三次握手(1) 第一次握手(2) 第二次握手(3) 第三次握手 2、TCP四次挥手(1) 一次挥手(2) 二次挥手(3) 三次挥手(4) 四次挥手 3、TCP滑动窗口4、TCP状态时序图5、多进程并发服务器6、多线程并发服务器 1、TCP三次握手 TCP三次握手(TCP three-way handshake)是TCP协…...

【云原生篇】K8S之Job 和 CronJob
在 Kubernetes (K8s) 中,Job 和 CronJob 是两种管理批处理任务的资源对象,它们用于控制短暂的一次性任务(Job)或定时执行的周期性任务(CronJob)。 Job 概念 Job 负责运行一个或多个 Pod,并确…...

PHP8.3-ZTS版本安装流程以及添加扩展
下载php-8.3.x.tar.gz至服务器并解压 [rootapisix-test php-8.3.4]# wget https://www.php.net/distributions/php-8.3.4.tar.gz进入目录执行编译命令,必须要带 --enable-zts 才能激活zts功能 [rootapisix-test php-8.3.4]# ./configure --prefix/usr/local/p…...

RabbitMQ系统监控、问题排查和性能优化实践
一、系统监控:RabbitMQ的各项性能指标及监控 Message Rates:消息率包含了publish,deliver/get,ack等方面的数据,反映了消息在系统中流转的情况。Queue Length:队列长度反映了系统当前的负载情况。如果队列…...
)
【华为OD机试】根据IP查找城市(贪心算法—JavaPythonC++JS实现)
本文收录于专栏:算法之翼 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目二.解题思路三.题解代码Python题解代码JAVA题解代码C/C++题解代码JS题解代码四.代码讲解(Ja…...

css:阴影效果box-shadow
属性 box-shadow 属性值由四个参数组成: 水平偏移量:表示阴影相对于元素的水平位置。垂直偏移量:表示阴影相对于元素的垂直位置。模糊度:表示阴影的模糊程度。颜色:表示阴影的颜色 示例 单个box-shadow 0px -2px 6p…...

Scala第十九章节(Actor的相关概述、Actor发送和接收消息以及WordCount案例)
Scala第十九章节 章节目标 了解Actor的相关概述掌握Actor发送和接收消息掌握WordCount案例 1. Actor介绍 Scala中的Actor并发编程模型可以用来开发比Java线程效率更高的并发程序。我们学习Scala Actor的目的主要是为后续学习Akka做准备。 1.1 Java并发编程的问题 在Java并…...

蓝桥杯杯赛之深度优先搜索优化《1.分成互质组》 《 2.小猫爬山》【dfs】【深度搜索剪枝优化】【搜索顺序】
文章目录 思想例题1. 分成互质组题目链接题目描述【解法一】【解法二】 2. 小猫爬山题目链接题目描述输入样例:输出样例:【思路】【WA代码】【AC代码】 思想 本质为两种搜索顺序: 枚举当前元素可以放入哪一组枚举每一组可以放入哪些元素 操…...

软件设计原则:依赖倒置
定义 依赖倒置原则(Dependency Inversion Principle, DIP)是面向对象设计原则之一,其核心是高层模块(如业务逻辑)不应当依赖于低层模块(如具体的数据访问或设备控制实现),而是双方都…...
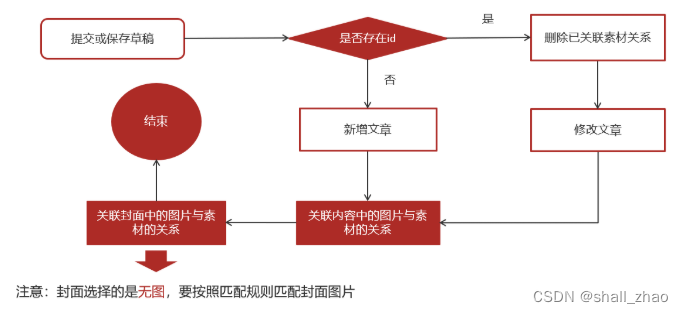
03-自媒体文章发布
自媒体文章发布 1)自媒体前后端搭建 1.1)后台搭建 ①:资料中找到heima-leadnews-wemedia.zip解压 拷贝到heima-leadnews-service工程下,并指定子模块 执行leadnews-wemedia.sql脚本 添加对应的nacos配置 spring:datasource:driver-class-name: com…...

Oracle中实现一次插入多条数据
一、需求描述 在我们实际的业务场景中,由于单条插入的效率很低(每次都需要数据库资源连接关闭的开销),故需要实现一次性插入多条数据,用以提升数据插入的效率; 如下图是常见的单条插入数据: 二…...
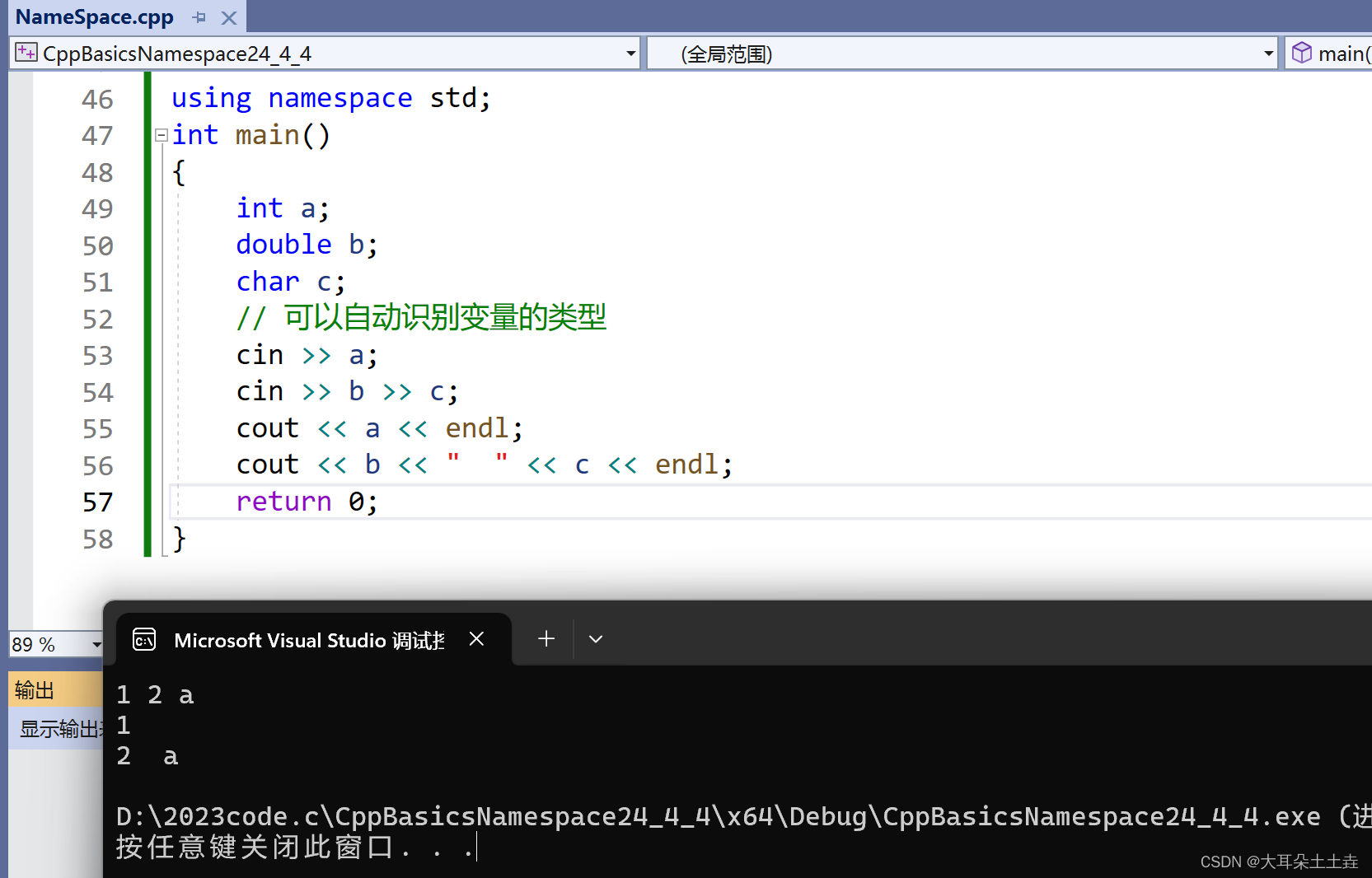
【C++入门】关键字、命名空间以及输入输出
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...

初识MySQL(中篇)
使用语言 MySQL 使用工具 Navicat Premium 16 代码能力快速提升小方法,看完代码自己敲一遍,十分有用 目录 1.SQL语言 1.1 SQL语言组成部分 2.MySQL数据类型 2.1 数值类型 2.2 字符串类型 2.3 日期类型 3.创建数据表 3.1 创建数据表方法1 …...
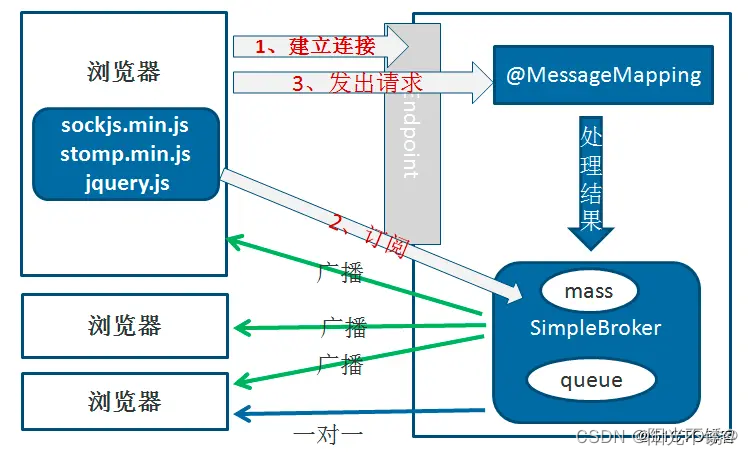
前端订阅后端推送WebSocket定时任务
0.需求 后端定时向前端看板推送数据,每10秒或者30秒推送一次。 1.前言知识 HTTP协议是一个应用层协议,它的特点是无状态、无连接和单向的。在HTTP协议中,客户端发起请求,服务器则对请求进行响应。这种请求-响应的模式意味着服务器…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
