Python常用算法思想--回溯算法思想详解【附源码】
通过回溯算法解决“组合”问题、“排序”问题、“搜索”之八皇后问题、“子集和”之0-1背包问题、字符串匹配等六个经典案例进行介绍:
一、解决“组合”问题

从给定的一组元素中找到所有可能的组合,这段代码中的 backtrack_combinations 函数使用了回溯思想,调用 backtrack_combinations 函数并返回结果。使用了一组给定的元素 [1, 2, 3, 4],并要求找到所有包含 3 个元素的组合,具体代码如下:
def backtrack_combinations(nums, k, start, path, result):
if k == 0:
result.append(path[:])
return
for i in range(start, len(nums)):
path.append(nums[i])
backtrack_combinations(nums, k - 1, i + 1, path, result)
path.pop()
def combinations(nums, k):
result = []
backtrack_combinations(nums, k, 0, [], result)
return result
# 测试示例
nums = [1, 2, 3, 4]
k = 3
print(f"All combinations of {k} elements from {nums}:")
print(combinations(nums, k))
二、解决“排序”问题
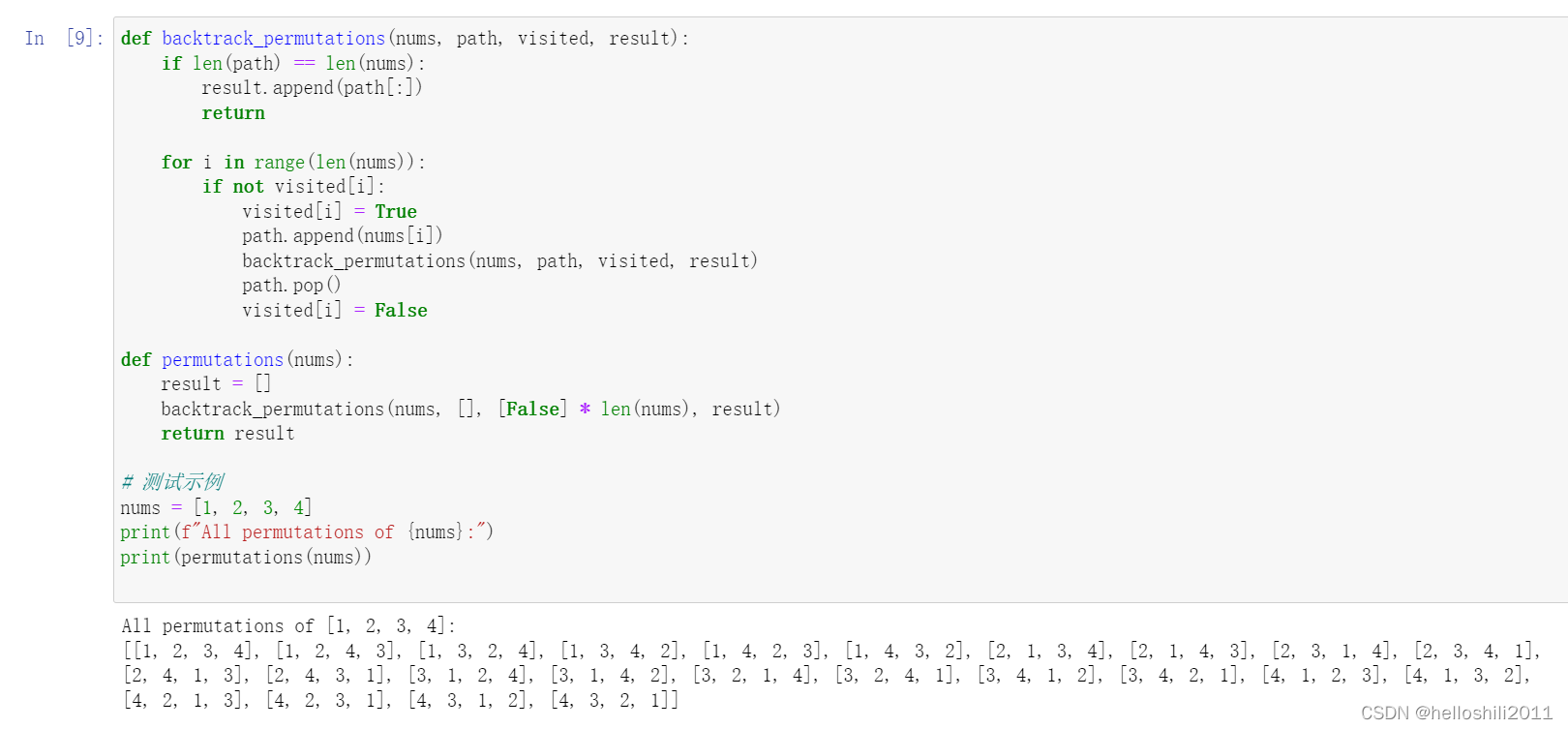
找到一组元素的所有可能的排列。这段代码中,backtrack_permutations 函数使用了回溯思想来递归地生成排列,调用 backtrack_permutations 函数并返回结果。使用了一组给定的元素 [1, 2, 3,4],并找到了所有可能的排列,具体代码如下:
def backtrack_permutations(nums, path, visited, result):
if
相关文章:

Python常用算法思想--回溯算法思想详解【附源码】
通过回溯算法解决“组合”问题、“排序”问题、“搜索”之八皇后问题、“子集和”之0-1背包问题、字符串匹配等六个经典案例进行介绍: 一、解决“组合”问题 从给定的一组元素中找到所有可能的组合,这段代码中的 backtrack_combinations 函数使用了回溯思想,调用 backtrack…...

Day5-Hive的结构和优化、数据文件存储格式
Hive 窗口函数 案例 需求:连续三天登陆的用户数据 步骤: -- 建表 create table logins (username string,log_date string ) row format delimited fields terminated by ; -- 加载数据 load data local inpath /opt/hive_data/login into table log…...

01 计算机网络发展与分类
计算机网络:计算机技术与通信技术的结合。 阶段一:早期网络:ARPAnet。 阶段二:厂商独立发展阶段 阶段三:标准化阶段:ISO,TCP/IP 计算机网络分类 计算机网络分类1:通信子网和资源子网 通信子…...
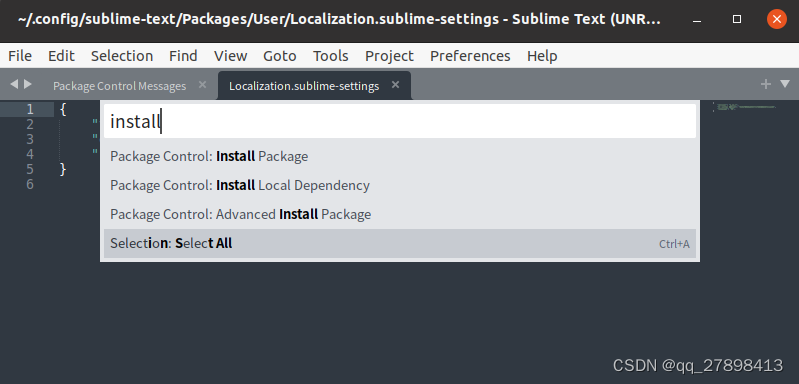
ubuntu安装sublime3并设置中文
安装Sublime Text 3 在Ubuntu上安装Sublime Text 3可以通过以下步骤进行: 打开终端。 导入Sublime Text 3的GPG密钥: wget -qO- https://download.sublimetext.com/sublimehq-pub.gpg | sudo apt-key add - 添加Sublime Text 3的存储库: …...
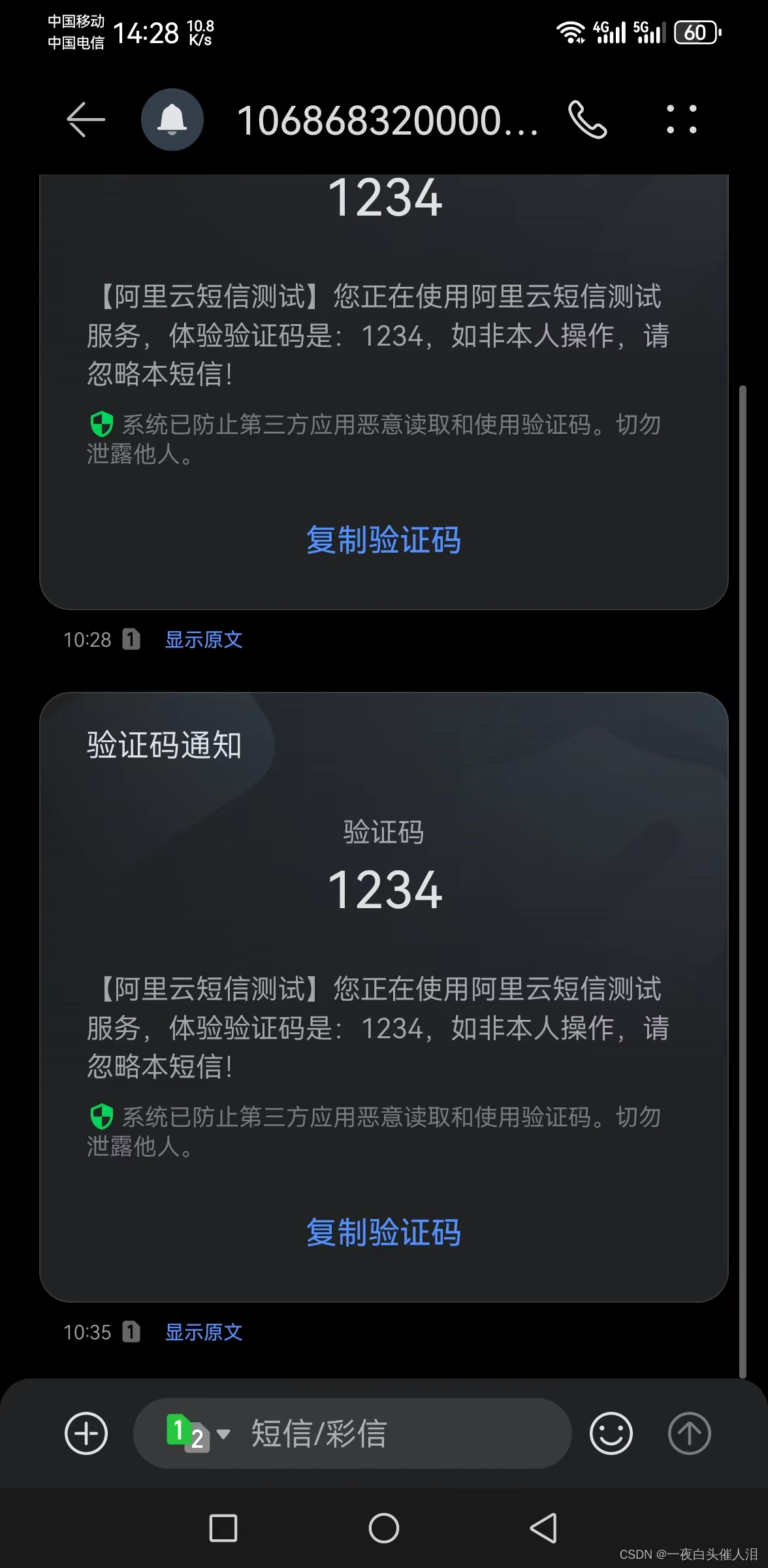
python调用阿里云短信配置
1. 新增资质和签名 # 访问地址: https://dysms.console.aliyun.com/domestic/text/qualification2. 静静等待几十分钟~~~ 3. 通过sdk去调用,查看有没有python的sdk https://next.api.aliyun.com/api/Dysmsapi/2017-05-25/SendSms?完整代码 # -*- cod…...
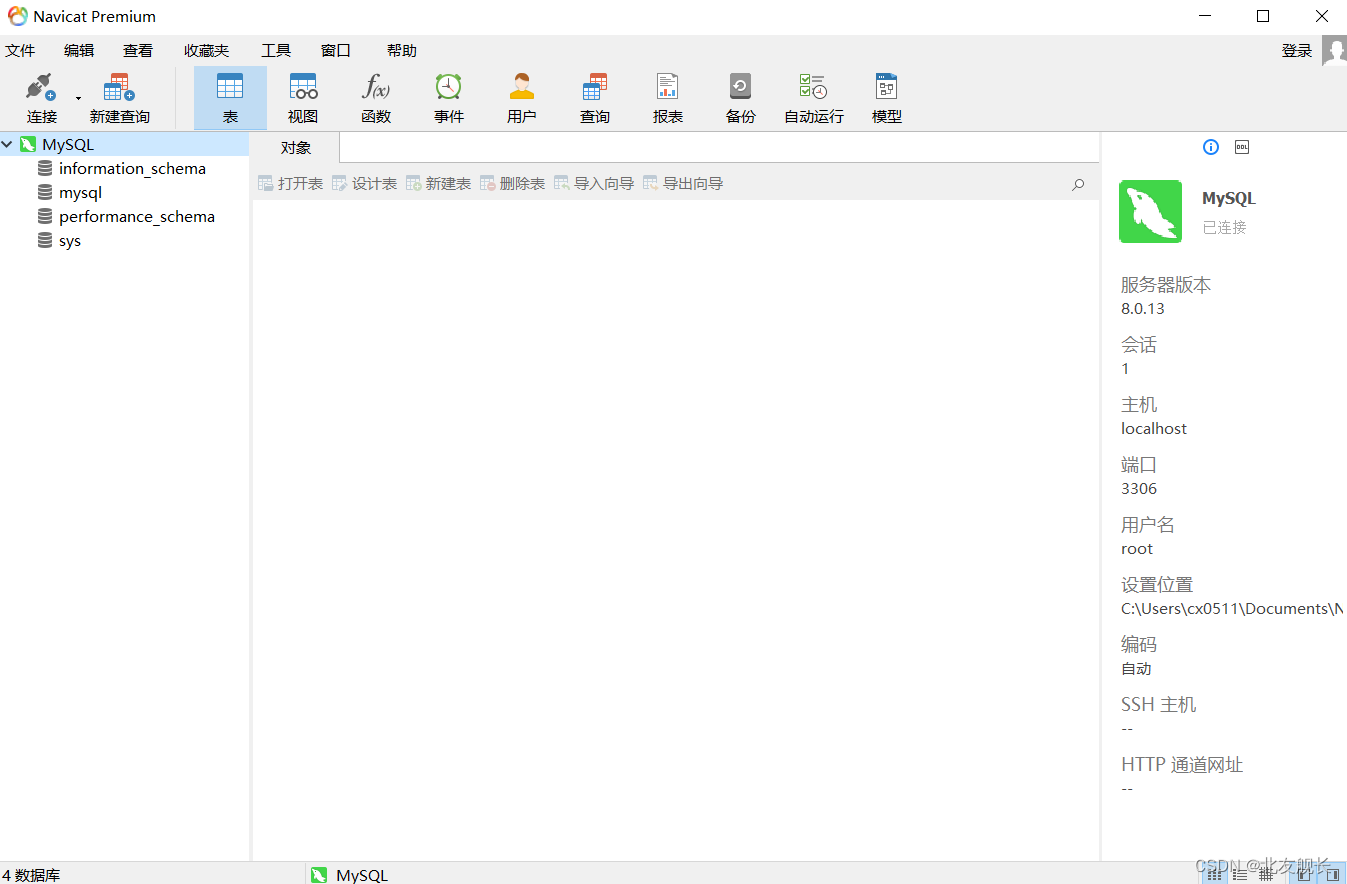
MySQL 8.0.13安装配置教程
写个博客记录一下,省得下次换设备换系统还要到处翻教程,直接匹配自己常用的8.0.13版本 1.MySQL包解压到某个路径 2.将bin的路径加到系统环境变量Path下 3.在安装根目录下新建my.ini配置文件,并用编辑器写入如下数据 [mysqld] [client] port…...
【idea快捷键】idea开发java过程中常用的快捷键
含义win快捷键mac快捷键复制当前行或选定的代码块Ctrl DCommand D通过类名快速查找类Ctrl NCommand N通过文件名快速查找文件Ctrl Shift NCommand Shift N通过符号名称快速查找符号(类、方法等)Ctrl Alt Shift NCommand Shift O跳转到声明C…...
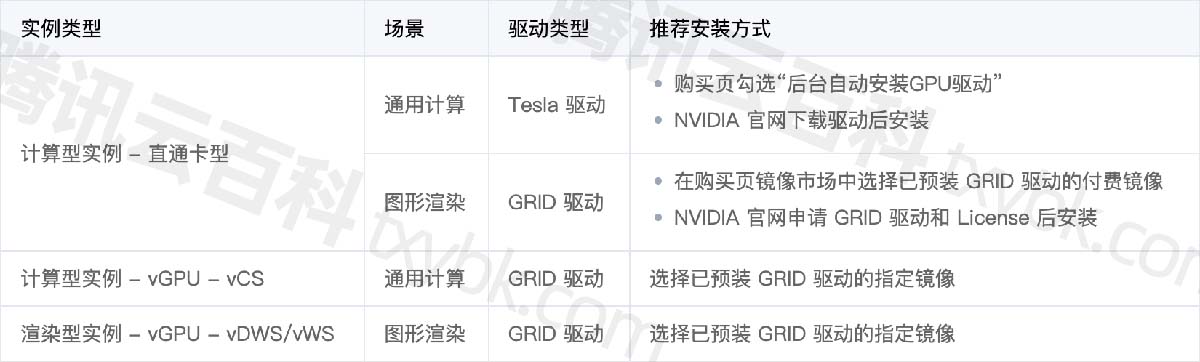
2024年腾讯云GPU云服务器配置价格表(内存/系统盘/地域)
腾讯云GPU服务器是提供GPU算力的弹性计算服务,腾讯云GPU服务器具有超强的并行计算能力,可用于深度学习训练、科学计算、图形图像处理、视频编解码等场景,腾讯云百科txybk.com整理腾讯云GPU服务器租用价格表、GPU实例优势、GPU解决方案、GPU软…...
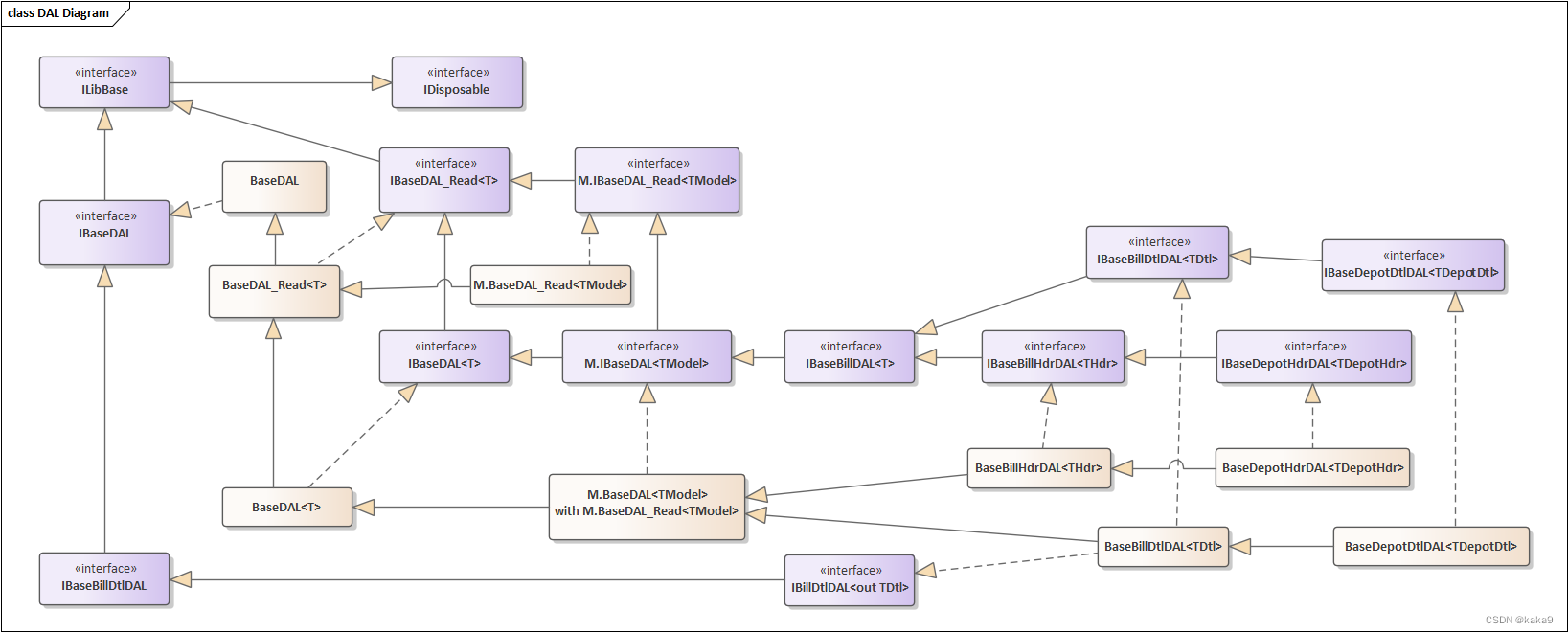
重构数据访问层-优化数据访问的开发
重新整理了一下过去开发的框架,在准备开发新项目时候,重新整理了一下思路,感觉数据访问层还是很鸡肋。过去几年中,急于完成项目开发和交付,框架都是迭代过来的,虽然满足了开发需求,但是…...

云计算概述报告
以下是一篇论述类文章 文章目录 I. 云计算介绍(1)云计算基本概念(2)云计算基本特征 II. 云计算发展历程(1)云计算的起源(2)云计算的发展阶段 III. 云计算特点(1ÿ…...

C++:线程库的使用
文章目录 Windows和Linux平台的线程线程构造函数模板参数包 最近发现C11的线程库还没有进行总结,因此本篇对于C11当中新增的线程库的一些基本用法进行总结 Windows和Linux平台的线程 在Linux平台下是存在一些原生的线程系统调用的,比如有pthread_creat…...

机器学习模型:决策树笔记
第一章:决策树原理 1-决策树算法概述_哔哩哔哩_bilibili 根节点的选择应该用哪个特征?接下来选什么?如何切分? 决策树判断顺序比较重要。可以使用信息增益、信息增益率、 在划分数据集前后信息发生的变化称为信息增益,…...
20.2k stars项目搭建私人网盘界面美功能全
Nextcloud是一套用于创建网络硬盘的客户端-服务器软件。其功能与Dropbox相近,但Nextcloud是自由及开放源代码软件,每个人都可以在私人服务器上安装并执行它。 GitHub数据 20.2k stars561 watching3.2k forks 开源地址:https://github.com/ne…...

卷积篇 | YOLOv8改进之引入全维度动态卷积ODConv | 即插即用
前言:Hello大家好,我是小哥谈。ODConv是一种关注了空域、输入通道、输出通道等维度上的动态性的卷积方法,一定程度上讲,ODConv可以视作CondConv的延续,将CondConv中一个维度上的动态特性进行了扩展,同时了考虑了空域、输入通道、输出通道等维度上的动态性,故称之为全维度…...
和torch.from_numpy(X_train).float()的区别)
Pytorch实用教程:torch.from_numpy(X_train)和torch.from_numpy(X_train).float()的区别
在PyTorch中,torch.from_numpy()函数和.float()方法被用来从NumPy数组创建张量,并可能改变张量的数据类型。两者之间的区别主要体现在数据类型的转换上: torch.from_numpy(X_train):这行代码将NumPy数组X_train转换为一个PyTorch张…...

深度学习pytorch好用网站分享
深度学习在线实验室Featurizehttps://featurize.cn/而且这个网站里面还有一些学习教程 免费好用 如何使用 PyTorch 进行图像分类https://featurize.cn/notebooks/5a36fa40-490e-4664-bf98-aa5ad7b2fc2f...
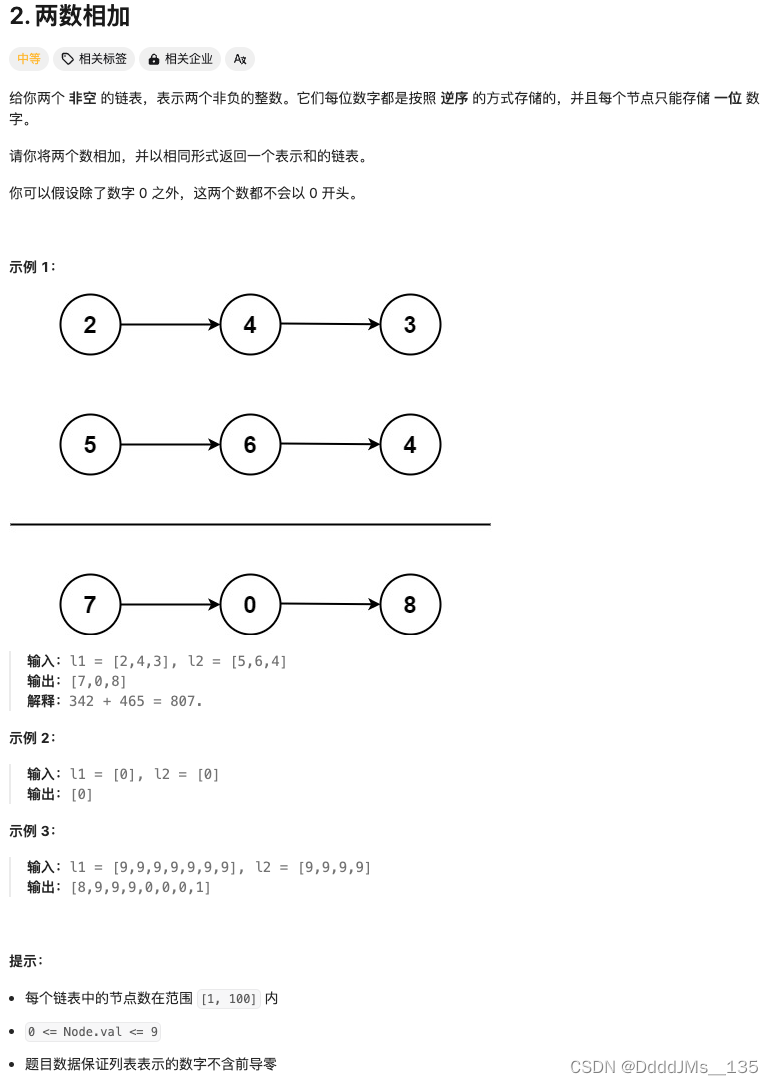
C语言 | Leetcode C语言题解之第2题两数相加
题目: 题解: struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2) {struct ListNode *head NULL, *tail NULL;int carry 0;while (l1 || l2) {int n1 l1 ? l1->val : 0;int n2 l2 ? l2->val : 0;int sum n1 n2 …...

Oracle基础
Oracle基础 Oracle,作为全球最大的数据库软件供应商,其数据库产品在企业级应用市场中占据了举足轻重的地位。Oracle数据库以高性能、高可用性、高安全性以及强大的数据管理能力赢得了广泛认可。本文旨在为读者提供Oracle数据库的基础知识,帮…...
从0到1实现RPC | 04 负载均衡和静态注册中心
一、Router的定义 Router路由用于预筛选,Dubbo有这样的设计,SpringCloud没有。 二、LoadBanlancer定义 负载均衡器:默认取第一个 当前支持随机和轮询两种负载均衡器。 随机:从所有provider中随机选择一个。 轮询:每…...

卷积神经网络-池化层
卷积神经网络-池化层 池化层(Pooling Layer)是深度学习神经网络中的一个重要组成部分,通常用于减少特征图的空间尺寸,从而降低模型复杂度和计算量,同时还能增强模型的不变性和鲁棒性。 池化操作通常在卷积神经网络&am…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
