数据分析之Logistic回归分析中的【多元有序逻辑回归】
1、定义
-
多元有序逻辑回归用于分析有序分类因变量与一个或多个自变量之间的关系。有序逻辑回归适用于因变量具有自然排序但没有固定间距的类别,例如疾病严重程度(轻度、中度、重度)或调查问卷中的满意度评分(非常不满意、不满意、一般、满意、非常满意)。
-
多元有序逻辑回归基于概率模型,它假设因变量的每个类别与一个潜在的连续变量(或称为对数优势)相关联。这个潜在变量的大小决定了观察到的有序分类结果。模型的目标是估计自变量对潜在变量的影响,以及它们如何影响因变量在不同有序类别之间的概率。
-
因变量的数量为N的有序逻辑回归,可以拆分为N-1 个二分类的Logistic回归模型。只是这N-1个模型中进行logit变换的不是响应变量每个类别的概率,而是响应变量有序取值水平的累积概率。模型需要满足一个非常重要的前提:风险比例假定。
假设因变量为疾病的严重程度:轻、中、重,分别赋值为1、2和3,那么因变量的拆分形式如下:
- 【1】 vs【 2、3】;
- 【1、2】 vs 【3】;
若因变量为4个等级1、2、3、4,那么则有:
- 【1】 vs 【2、3、4】;
- 【1、2】 vs 【3、4】;
- 【1、2、3 】vs 【4】。
知识补充:
- 风险比例假定:
- 自变量对于因变量中相邻有序类别的风险比例(即优势比,Odds Ratio)的影响是一致的。这意味着,自变量对于因变量的每个有序级别之间的风险比例变化是成比例的。
- 即不论响应变量从哪个水平进行切分,拟合的N-1个二分类的logistic回归模型只有截距不同,而各个解释变量的系数均保持一致。
- 而平行线检验可判断模型是否满足风险比例假定,当平行线检验的P值>0.05时(注意:此处为大于0.05,并非小于0.05,根据原假设判断)即满足风险比例假定,那么模型的结果将更加可靠,可以用于解释自变量对因变量有序类别风险比例的影响。若不满足平行线检验,建议使用多元无序逻辑回归进行分析。
- 平行线检验
- 定义:
平行线检验,也称为比例优势假设检验,是在使用有序逻辑回归(包括多元有序逻辑回归)时进行的一个重要步骤。这个假设检验是为了验证模型中的自变量对于因变量的不同类别之间的边界(cut-off points)是否有一致的影响。 - 原假设(H0):
平行线检验的原假设是,所有自变量对于因变量的相邻类别之间的对数优势(log odds)的影响是相同的。换句话说,自变量对于因变量中相邻有序类别的相对风险(odds)的对数是恒定的,即自变量对于对数优势的影响在所有有序类别的边界上是一致的。根据原假设可知,当平行线检验的P值>0.05时接受原假设,即满足风险比例假定。
2、用法
在使用多元有序逻辑回归时,首先需要满足几个条件:
- 因变量是有序的,且类别间存在自然排序。
- 自变量可以是连续的,也可以是分类的。
- 数据应该是独立的,即每个观测值的结果不受其他观测值的影响。
- 自变量之间不存在多重共线性。
- 比例优势假设得到满足,即自变量对因变量的影响在所有有序类别的边界上是一致的。
3、使用场景
多元有序逻辑回归常用于以下场景:
- 医学研究中评估不同因素对疾病严重程度的影响。
- 社会科学中分析个体特征对满意度或态度的影响。
- 市场研究中了解不同因素如何影响消费者的产品评价等级。
相关文章:

数据分析之Logistic回归分析中的【多元有序逻辑回归】
1、定义 多元有序逻辑回归用于分析有序分类因变量与一个或多个自变量之间的关系。有序逻辑回归适用于因变量具有自然排序但没有固定间距的类别,例如疾病严重程度(轻度、中度、重度)或调查问卷中的满意度评分(非常不满意、不满意、…...
路由器拨号失败解决方法
目录 一、遇到问题 二、测试 三、解决方法 (一)路由器先单插wan口设置 (二)mac地址替换 (三)更改路由器DNS 一、遇到问题 1 .在光猫使用桥接模式,由路由器进行拨号的时候,出现…...
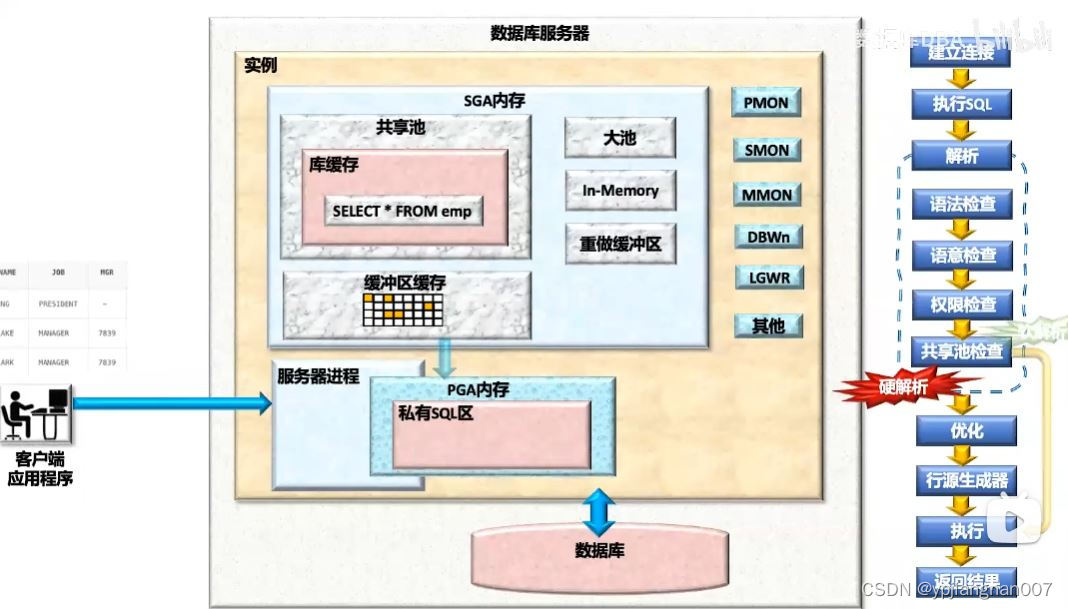
Oracle 中 where 和 on 的区别
1.Oracle 中 where 和 on 的区别 on:会先根据on后面的条件进行筛选,条件为真时返回该行,由于on的优先级高于left join,所以left join关键字会把左表中没有匹配的所有行也都返回,然后生成临时表返回,执行优先级高于…...

NLP学习路线总结
自然语言处理(Natural Language Processing,NLP)是人工智能和语言学领域的一部分,它旨在让计算机能够理解、解释和生成人类语言。NLP学习路线可以大致分为以下几个步骤: 1. 基础知识准备 - 计算机科学知识:…...
AI绘图cuda与stable diffusion安装部署始末与避坑
stable diffusion的安装说起来很讽刺,最难的不是stable diffusion,而是下载安装cuda。下来我就来分享一下我的安装过程,失败了好几次,几近放弃。 一、安装cuda 我们都知道cuda是显卡CPU工作的驱动(或者安装官网的解释…...
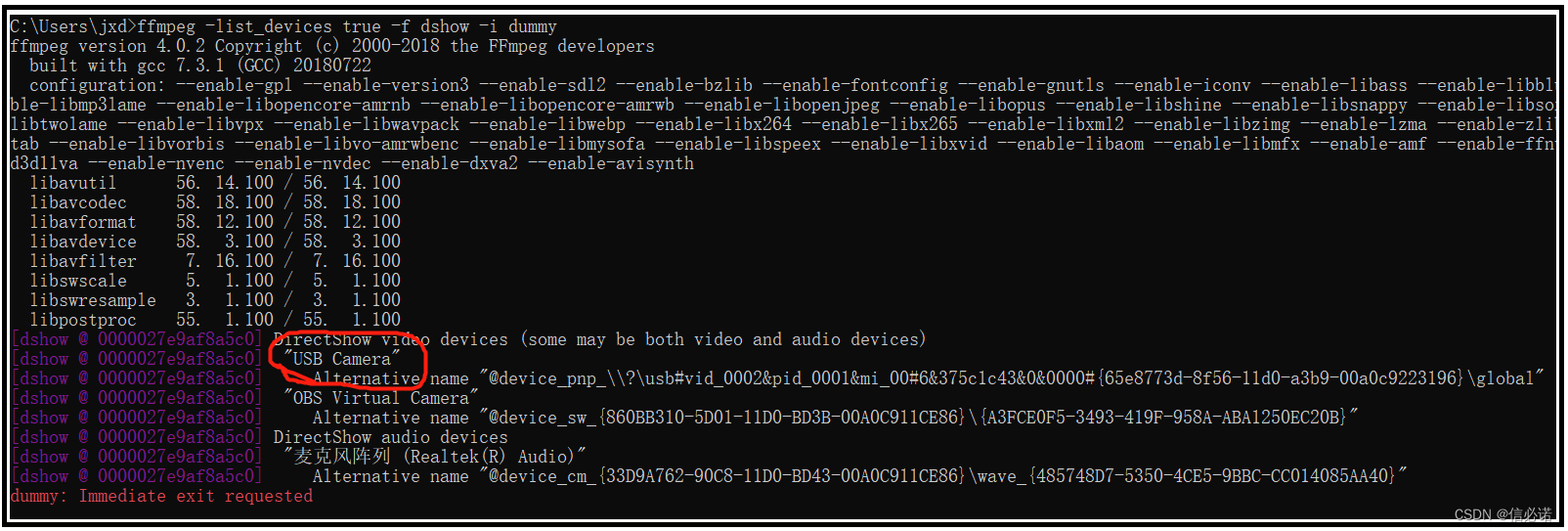
OpenCv —— cv::VideoCapture设置摄像头图像格式为“MJPEG“
背景 今天恰巧同事有台USB摄像头,她想要在Windows系统下通过OpenCV读取该摄像头宽高为1080x768、帧率为60的视频,用来做图像算法处理。但无奈通过网上OpenCV教程 读取的视频对应尺寸的帧率仅为10帧左右,根本无法满足使用要求。于是作者通过本篇文章介绍如何解决,欢迎交流指…...

Qt事件学习案例
视频链接 https://www.bilibili.com/video/BV18B4y1K7Cs?p7&spm_id_frompageDriver&vd_sourcefa4ef8f26ae084f9b5f70a5f87e9e41bQt5跟着视频做即可,Qt6部分代码需要改动,改动的地方注释有写 素材 百度云 链接:https://pan.baidu.com/s/158j…...

无锡国家集成电路设计中心某公司的单锂小电机直流电机H桥驱动电路
H桥驱动 L9110S是一款直流电机驱动电路,适合单节锂电池应用。输出电流0.4A。价格约3毛。 推荐原因: 某些人应该知道这个地方,大多数人应该不知道这个地方,所以推荐一下。 这个地方去过几次,某公司与某方走的“近”&…...

数据分析 -- numpy
文章目录 numpy库简介简介特点 numpy操作数组创建数组属性数组变更数据计算 numpy库简介 简介 开源的Python库,它提供了高性能的多维数值(numpy.ndarray)计算能力;由“Numerical Python”缩写而来,并且它是Pandas库的…...

开源项目生存现况:xz投毒事件引发的思考与GNU tar维护挑战
(首发地址:学习日记 https://www.learndiary.com/2024/04/xz-tar/) 嗨,大家好!我是来自淘宝网“学习日记小店”的 learndiary,专注于 Linux 服务领域。今天我要和大家谈谈近期备受瞩目的 XZ 供应链投毒事件…...

前端开发语言有哪些
随着互联网的迅猛发展,前端开发已经成为了一个炙手可热的职业。对于初学者来说,了解前端开发所使用的语言是非常重要的。那么,前端开发语言有哪些呢?本文将为您一一介绍。 一、HTML HTML(HyperText Markup Language&…...

速盾:cdn加速https额外收费吗?
CDN(内容分发网络)是一种通过在全球各地部署服务器来提供高速互联网内容传输的技术,它可以加速网站的访问速度,提高用户体验。而HTTPS(超文本传输安全协议)是一种通过加密技术保护网站数据传输安全的协议。…...
【蓝桥杯嵌入式】13届程序题刷题记录及反思
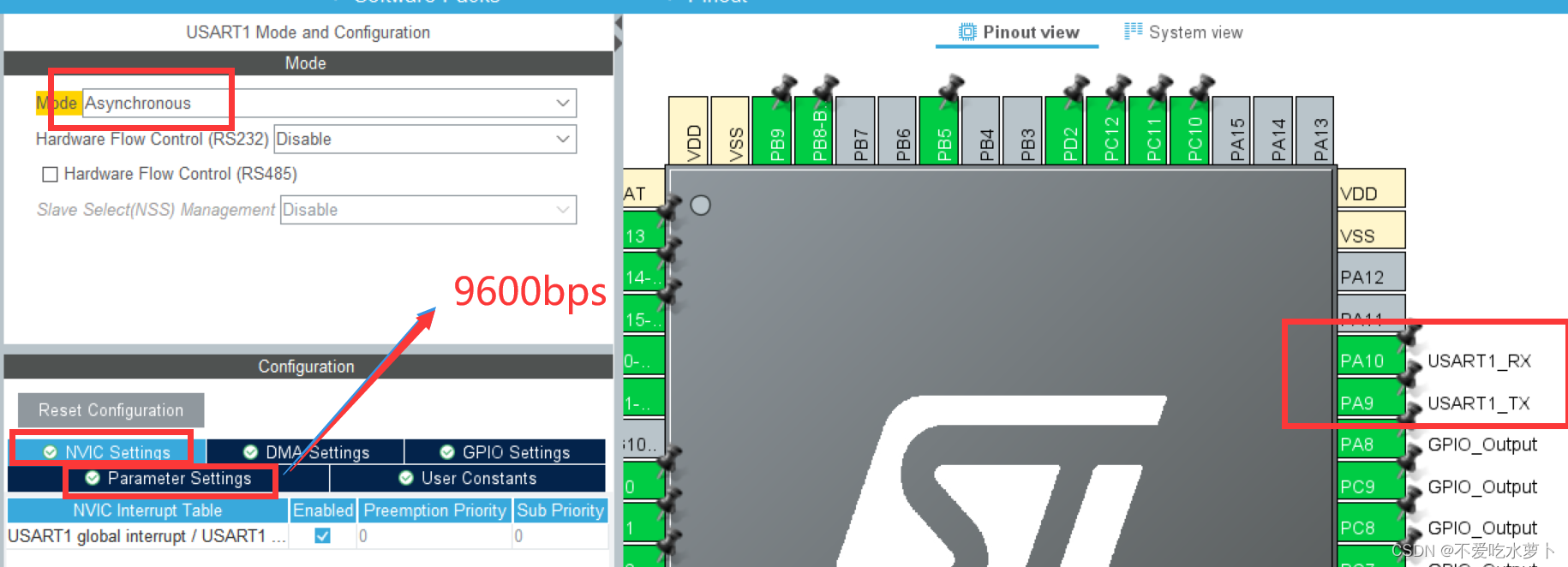
一、题目分析 考察内容: led按键(短按)PWM输出(PA1)串口接收lcd显示 根据PWM输出占空比调节,高频与低频切换 串口接收(指令解析)【中断接收】 2个显示界面 led灯闪烁定时器 二…...

C++类 单例模式
例子 请看如下的类和调用: 在您提供的代码片段中,CPathPlanMan 类使用了一个单例模式,这意味着这个类只需要一个实例,并且提供了全局访问点来获取这个实例。这通常用于控制对一个类实例的访问,尤其是在创建实例代价昂…...
prompt 工程案例
目录 prompt 工程是什么? 案例 vllm 推理加速框架 prompt 工程是什么? prompt:提示词,也就是我们使用网页版输入给大模型的内容就叫 prompt,那什么是 prompt 工程呢? 简单理解其实就是利用编写的 prom…...

燃气管网安全运行监测系统功能介绍
燃气管网,作为城市基础设施的重要组成部分,其安全运行直接关系到居民的生命财产安全和城市的稳定发展。然而,随着城市规模的不断扩大和燃气使用量的增加,燃气管网的安全运行面临着越来越大的挑战。为了应对这些挑战,燃…...

正则表达式(2)
文章目录 专栏导读1、贪婪与非贪婪2、转义匹配 专栏导读 ✍ 作者简介:i阿极,CSDN 数据分析领域优质创作者,专注于分享python数据分析领域知识。 ✍ 本文录入于《python网络爬虫实战教学》,本专栏针对大学生、初级数据分析工程师精…...

xv6源码分析 001
xv6源码分析 001 我们先看看xv6这个项目的基本结构(只看代码部分) 主要就是两个目录kernel 和 user。 user是一些用户程序,也就是我们平时在shell上面执行的命令,每执行一个命令就会创建一个新的用户进程来执行这个命令 在user目…...
)
JS代码小知识(个人向)
JS 对象转数组 let obj {0:"a",1:"b",length:2 //加上这个就能转了 }; console.log(Array.from(obj)); // ["a", "b"] 数组的拼接 let a ["a","b"] let b ["c","d"] let c [...a , …...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

)