矩阵空间秩1矩阵小世界图
文章目录
- 1. 矩阵空间
- 2. 微分方程
- 3. 秩为1的矩阵
- 4. 图
1. 矩阵空间
我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。
- 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间
- 上三角矩阵-子空间-有6个3X3的上三角矩阵,所以为6维矩阵空间
矩阵M的基础基有9个,表示如下
[ 1 0 0 0 0 0 0 0 0 ] ; [ 0 1 0 0 0 0 0 0 0 ] ; [ 0 0 1 0 0 0 0 0 0 ] ; [ 0 0 0 1 0 0 0 0 0 ] ; (1) \begin{bmatrix}1&0&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&1&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&1\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\1&0&0\\\\0&0&0\\\\\end{bmatrix};\tag{1} 100000000 ; 000100000 ; 000000100 ; 010000000 ;(1)
[ 0 0 0 0 1 0 0 0 0 ] ; [ 0 0 0 0 0 1 0 0 0 ] ; [ 0 0 0 0 0 0 1 0 0 ] ; [ 0 0 0 0 0 0 0 1 0 ] ; [ 0 0 0 0 0 0 0 0 1 ] ; (2) \begin{bmatrix}0&0&0\\\\0&1&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&1\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\1&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&1&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&0&1\\\\\end{bmatrix};\tag{2} 000010000 ; 000000010 ; 001000000 ; 000001000 ; 000000001 ;(2)
2. 微分方程
- 假设我们有如下微分方程:
d 2 y d x 2 + y = 0 (3) \frac{\mathrm{d}^2y}{\mathrm{d}x^2}+y=0\tag{3} dx2d2y+y=0(3) - 零空间解表示如下:
y 1 = sin ( x ) ; y 2 = cos ( x ) (4) y_1=\sin(x);y_2=\cos(x)\tag{4} y1=sin(x);y2=cos(x)(4) - 通解表示如下:
y = c 1 sin ( x ) + c 2 cos ( x ) (5) y=c_1\sin(x)+c_2\cos(x)\tag{5} y=c1sin(x)+c2cos(x)(5)
以上可以用 sin ( x ) \sin(x) sin(x)和 cos ( x ) \cos(x) cos(x)当做解来表示解空间,所以微分方程的解空间为2.
3. 秩为1的矩阵
假设我们有一个秩为1的矩阵A ,表示如下:
A = [ 1 4 5 2 8 10 ] = [ 1 2 ] 2 × 1 [ 1 4 5 ] 1 × 3 (6) A=\begin{bmatrix}1&4&5\\\\2&8&10\end{bmatrix}=\begin{bmatrix}1\\\\2\end{bmatrix}_{2\times1}\begin{bmatrix}1&4&5\end{bmatrix}_{1\times3}\tag{6} A= 1248510 = 12 2×1[145]1×3(6)
- 所有的秩为1的矩阵均可以分解为列向量乘以行向量。
- 小结:
我们可以通过组合秩为1的矩阵来构造我们想要的秩的矩阵。
4. 图
我们知道一个图可以有节点和边组成
G r a p h = [ n o d e s , e d g e s ] (7) Graph=[nodes,edges]\tag{7} Graph=[nodes,edges](7)

相关文章:

矩阵空间秩1矩阵小世界图
文章目录 1. 矩阵空间2. 微分方程3. 秩为1的矩阵4. 图 1. 矩阵空间 我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间上三角矩阵-子空间-有6个3…...
《QT实用小工具·十三》FlatUI辅助类之各种炫酷的控件集合
1、概述 源码放在文章末尾 FlatUI辅助类之各种炫酷的控件集合 按钮样式设置。文本框样式设置。进度条样式。滑块条样式。单选框样式。滚动条样式。可自由设置对象的高度宽度大小等。自带默认参数值。 下面是demo演示: 项目部分代码如下所示: #ifnd…...
dm8 备份与恢复
dm8 备份与恢复 基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例1 设置bak_path路径 --创建备份文件存放目录 su - dmdba mkdir -p /dm8/backup--修改dm.ini 文件…...
Vue项目中引入html页面(vue.js中引入echarts数据大屏html [静态非数据传递!] )
在项目原有vue(例如首页)基础上引入html页面 1、存放位置 vue3原有public文件夹下 我这边是新建一个static文件夹 专门存放要用到的html文件 复制拖拽过来 index为html的首页 2、更改路径引入到vue中 这里用到的是 iframe 方法 不同于vue的 component…...

ASTM C1186-22 纤维水泥平板
以无石棉类无机矿物纤维、有机合成纤维或纤维素纤维,单独或混合作为增强材料,以普通硅酸盐水泥或水泥中添加硅质、钙质材料代替部分水泥为胶凝材料,经制浆、成型、蒸汽或高压蒸汽养护制成的板材,俗称水泥压力板。 ASTM C1186-22纤…...

NoSQL概述
NoSQL概述 目录 一、为什么用NoSQL 二、什么是NoSQL 三、经典应用分析 四、N o S Q L 数 据 模 型 简 介 五、NoSQL四大分类 六、CAP BASE 一、为什么用NoSQL 1、单机MySQL的美好年代 在90年代,一个网站的访问量一般不大,用单个数据库完全可以轻松应…...
爬虫实战一、Scrapy开发环境(Win10+Anaconda3)搭建
#前言 在这儿推荐使用Anaconda进行安装,并不推荐大家用pythonpip安装,因为pythonpip的坑实在是太多了。 #一、环境中准备: Win10(企业版)Anaconda3-5.0.1-Windows-x86_64,下载地址,如果打不开…...
llama.cpp运行qwen0.5B
编译llama.cp 参考 下载模型 05b模型下载 转化模型 创建虚拟环境 conda create --prefixD:\miniconda3\envs\llamacpp python3.10 conda activate D:\miniconda3\envs\llamacpp安装所需要的包 cd G:\Cpp\llama.cpp-master pip install -r requirements.txt python conver…...
 |GET和POST两种基本请求方法有什么区别)
【接口】HTTP(3) |GET和POST两种基本请求方法有什么区别
在我面试时,在我招人面试别人时,10次能遇到7次这个问题,我听过我也说回答过: Get: 一般对于从服务器取数据的请求可以设置为get方式 Get方式在传递参数的时候,一般都会把参数直接拼接在url上 Get请求方法…...

金陵科技学院软件工程学院软件工程专业
感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦…...

Android 关于apk反编译d2j-dex2jar classes.dex失败的几种方法
目录 确认路径正确直接定位到指定目录确定目录正确,按如下路径修改下面是未找到相关文件正确操作 确认路径正确 ,即d2j-dex2jar和classes.dex是否都在一个文件夹里(大部分的情况都是路径不正确) 直接定位到指定目录 路径正确的…...

Django--admin 后台管理站点
Django最大的优点之一,就是体贴的提供了一个基于项目model创建的一个后台管理站点admin。这个界面只给站点管理员使用,并不对大众开放。虽然admin的界面可能不是那么美观,功能不是那么强大,内容不一定符合你的要求,但是…...

JavaScript(六)---【回调、异步、promise、Async】
零.前言 JavaScript(一)---【js的两种导入方式、全局作用域、函数作用域、块作用域】-CSDN博客 JavaScript(二)---【js数组、js对象、this指针】-CSDN博客 JavaScript(三)---【this指针,函数定义、Call、Apply、函数绑定、闭包】-CSDN博客 JavaScript(四)---【执…...
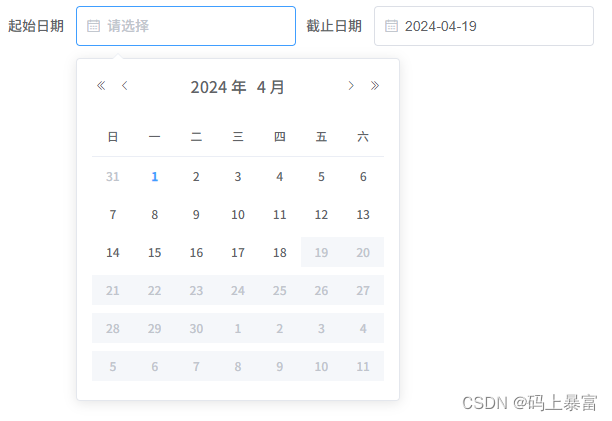
vue2+elementUi的两个el-date-picker日期组件进行联动
vue2elementUi的两个el-date-picker日期组件进行联动 <template><el-form><el-form-item label"起始日期"><el-date-picker v-model"form.startTime" change"startTimeChange" :picker-options"startTimePickerOption…...

GIN实例讲解
第一个gin程序 package mainimport ("github.com/gin-gonic/gin" )func main() {// 创建一个 Gin 引擎实例r : gin.Default()// 定义一个 GET 请求的路由,当访问 /hello 路径时执行匿名函数r.GET("/hello", func(c *gin.Context) {// 获取查询…...

开源充电桩设备监控系统技术解决方案
开源 | 慧哥充电桩平台V2.5.2(支持 汽车 电动自行车 云快充1.5、云快充1.6 微服务 ) SpringBoot设备监控系统解决方案 一、引言 1.项目背景 随着物联网技术的快速发展,设备的智能化和网络化程度日益提高。在现代工业和信息化的背景下&#x…...
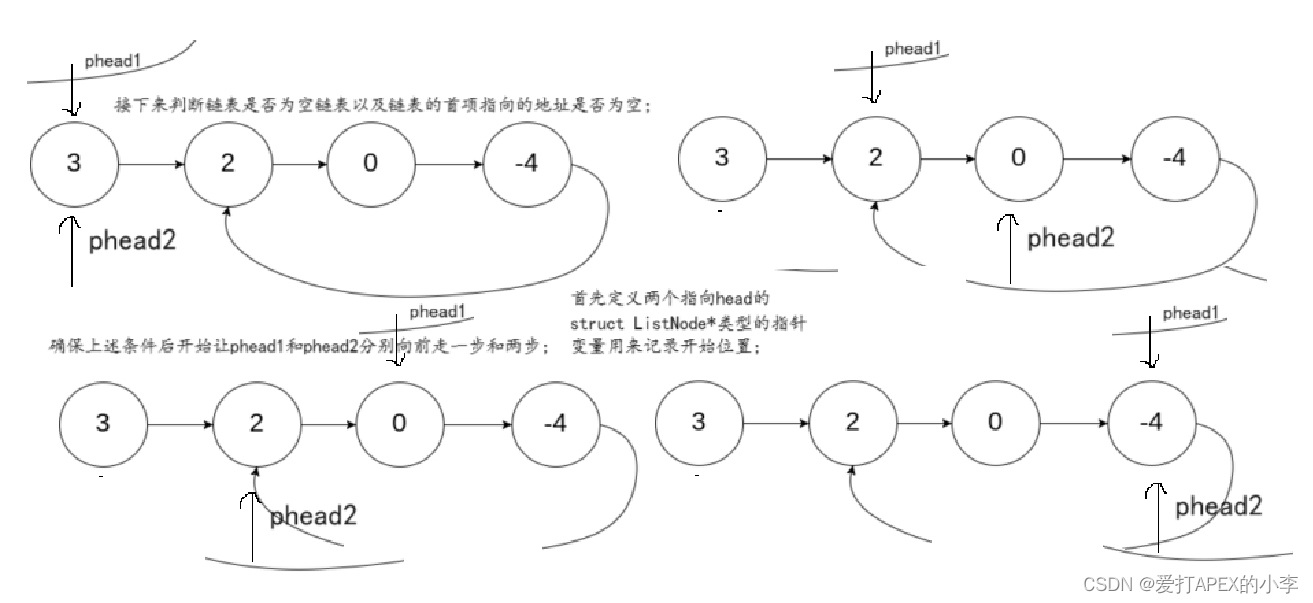
环形链表--极致的简便
一、要求 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&a…...

WPF中TextWrapping
在 WPF(Windows Presentation Foundation)中,TextWrapping 是一个与文本布局相关的属性,用于控制文本在遇到容器边界时是否自动换行。这个属性常用于文本展示控件,如 TextBlock、TextBox、Label 等,以确保文…...
Win10 下 git error unable to create file Invalid argument 踩坑实录
原始解决方案参看:https://stackoverflow.com/questions/26097568/git-pull-error-unable-to-create-file-invalid-argument 本问题解决于 2024-02-18,使用 git 版本 2.28.0.windows.1 解决方案 看 Git 抛出的出错的具体信息,比如如下都来自…...
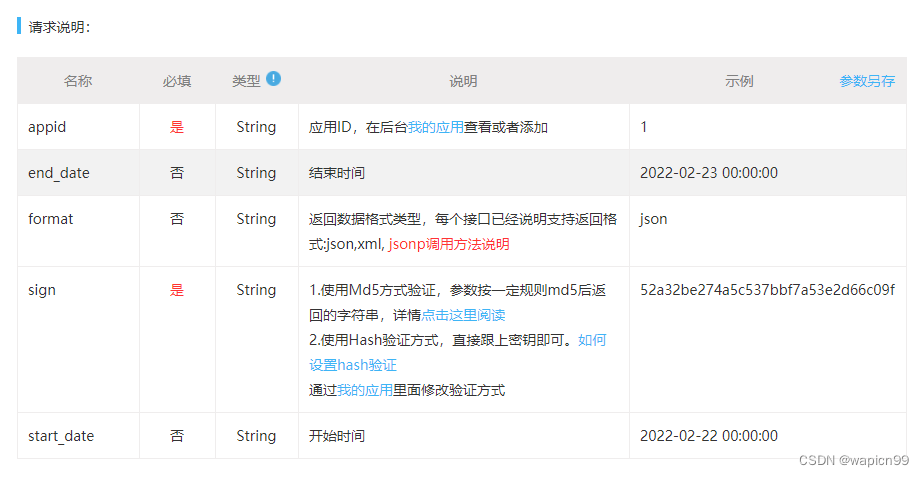
简化备案域名查询的最新API接口
随着互联网的发展,越来越多的网站和域名被注册和备案。备案域名查询是一个非常重要的功能,可以帮助用户在特定时间段内查询已备案的域名信息。现在,我将介绍一个简化备案域名查询的最新API接口,该接口可以帮助用户快速查询备案域名…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
