2013年认证杯SPSSPRO杯数学建模C题(第二阶段)公路运输业对于国内生产总值的影响分析全过程文档及程序
2013年认证杯SPSSPRO杯数学建模
C题 公路运输业对于国内生产总值的影响分析
原题再现:
交通运输作为国民经济的载体,沟通生产和消费,在经济发展中扮演着极其重要的角色。纵观几百年来交通运输与经济发展的相互关系,生产水平越高,就越要求基础结构超前发展。工业化时期的基础结构,已经不允许交通运输滞后。进入现代化社会,经济社会对交通运输的要求本质上就是超前的,交通运输是国民经济的先行官,发展经济,交通先行,是经济发展的内在规律。公路运输是在公路上运送旅客和货物的运输方式,是交通运输系统的组成部分之一,主要承担中短途客货运输。发展公路运输对国内生产总值(GDP)增长的贡献产生于交通建设和客货运输两个阶段,表现为公路运输对国民经济的直接贡献、波及效果、对于相关行业的直接消费以及创造就业机会等几个方面。
某省的统计部门想通过调查研究的方法估计公路运输业对于 GDP 的影响,通过随机发放问卷,获得了附件 1 中所示的数据,该数据为真实调查得到的原始数据。请参照该数据完成如下问题:
第二阶段问题:
问题 3 附件 3 给出了该省主要城市的公路运输统计数据。请建立合理的数学模型,给出未来五年公路运输投资资金在各市的分配比例。
问题 4 请根据附件 3 给出的数据,对于问题 1 的结果进行修正,详细陈述修正的理由。
整体求解过程概述(摘要)
本文研究的是关于公路运输业对于国内生产总值影响的问题,通过分析题目所给的数据建立了无量纲标准化模型、指数平滑的时间序列模型、灰色系统模型、曲线拟合模型、聚类分析模型、效益综合模型、改进加权主成分分析法模型、熵权的属性识别模型、误差修正模型、时间序列的单位根检验模型、协整分析模型,利用 MATLAB 软件和 SPSS软件对上述模型进行逐一求解,分别回答了题目所给的所有问题。
针对问题三,首先利用 SPSS 软件对原始数据填补缺失值和分析异常值,并用无量纲化处理方法对公路运输指标进行分类和标准化。再用指数平滑的时间序列模型、灰色系统模型、曲线拟合投资值变化趋势法分别预测公路运输投资强度,得到未来 5 年公路投资强度分别为:74.7514、74.6070、72.0358、67.2308 和 60.5528。然后用聚类城市等级量化模型对经济效果影响不同的城市进行投资力度分类(其分类效果详见 9 页),进而利用加权主成分分析法求解出各类城市对该省经济效果的贡献值。最后综合各市投资增长率、公路运输投资强度及其经济效果贡献值用熵权分析法求解出未来 5 年各城市公路建设资金投入的具体比例(详见 14 页)。
针对问题四,为了结合附件所给的数据将公路运输业对 GDP 的影响模型进行合理的修正,首先通过公路投资与国民经济发展指标的相关分析得到一般性相关关系。其次通过 Engle—Granger 两步法分析公路投资与国民经济发展指标的协整过程得出公路投资与国民经济发展之间形成了长期均衡关系。然后利用 Granger 因果关系检验 Engle—Granger 两步法所得结论得出其模型的正确性和精确度。最后得出公路投资额与国民经济发展指标 GDP 之间有着高度的正相关关系。
问题分析:
根据这个问题的实际背景和现有的抽检数据,首先依据 2007 年到 2011 年公路运输的统计数据对该省 11 个城市的投资情况进行强度分类,再结合历年公路投资的强度变化作预测分析,利用改进的加权主成分析法模型推算出 11 个城市经济效益综合贡献值。从而结合熵权算法模型求解出未来 5 年该省每个城市公路投资比例;最后结合上述问题分析的公路运输对 GDP 的影响模型,利用相关分析以及循环检验更深入的讨论了公路运输业对 GDP 的影响效益。
问题 1)通过题目所给附件的信息,结合问题的求解进行了合理的等级分类,利用将原始处理进行缺失值和异常值的处理,再根据分类标准进行数据整合。首先通过历年公路投资强度进行逐步预测分析,从而得到未来 5 年该省公路投资强度的变化情况,再根据前 5 年各城市的投资强度,利用 SPSS 软件进行聚类分析,从而得到重投入、较重投入、轻投入和最小投入所代表性的城市,通过改进后的加权主成分析法模型求解出各城市公路运输对经济效益的综合贡献值。最后结合投入增长率、城市经济贡献值和城市建设强度值,利用熵权分析模型求解出未来 5 年各城市公路建设资金投入的具体比例,
问题 2) 通过对上述公路运输对 GDP 影响模型的分析,结合附件 3 中 2007 年到2011 年公路运输统计的数据进行模型修正。首先结合公路投资强度值和 GDP 的相关数据初步分析出公路运输投资与 GDP 的相关性,再通过公路投资与国民经济协整关系分析及误差修正模型、公路投资额与 GDP 时间序列的单位根检验、公路投资额与 GDP 的协整分析和公路投资额与 GDP 的协整分析一系列步骤深入的分析公路运输对 GDP 的影响,最后结合检验环节更好的证明了上述分析的正确性。
模型假设:
1.假设本文附件中的缺失值和异常值是由于工作人员的忽视而造成了,而通过处理后的异常和缺失数据与原始数据差异性不大。
2.假设该省每个城市公路建设投资的强度与城市公路经济贡献效益成正相关。
3.假设将该省 11 个城市公路投资的强度划分为最低投入、低投入、较高投入和高投入四各等级进行分析。
4.假设该省公路投资金额用公路投资强度来确定,其中公路里程增加的值与单位面积公路建设资金相乘表示公路投资强度。
5.假设未来 5 年该省各城市公路投资总强度由 11 个城市公路效益经济综合值、城市建设权重和未来 5 年该省公路投资变化率来决定。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
1.
x=[0:1:4];
y=[1.654277124 1.728771002 1.776948578 1.839460144 1.859779993];
y1=1.631022+0.175439*x;
plot(x,y,'--',x,y1,'-*');
title('¹预测曲线');
xlabel('时间');
ylabel('预测值');
grid on;
2.
B=[-287.0063459 1
-515.6540044 1
-773.3170607 1
-1055.69827 1];
B1=[-287.0063459 -515.6540044 -773.3170607 -1055.69827
1 1 1 1];
Y=[54.5320405
59.79178874
69.03973939
72.15086514];
q=inv(B1*B)*B1*Y
3.曲线方程
x=[0:1:4];
y=[44.48556623 54.5320405 59.79178874 69.03973939 72.15086514];
y1=2037.407*(exp(0.0241*x)-exp(0.0241*(x-1)));
plot(x,y,'--',x,y1,'-*');
title('预测曲线图');
xlabel('时间');
ylabel('预测值');
grid on;
4.
x=[0:1:4];
y=[44.48556623 54.5320405 59.79178874 69.03973939 72.15086514];
cftool
5.
x=[0:1:4];
y=[44.48556623 54.5320405 59.79178874 69.03973939 72.15086514];
y3=2.064e+005*exp(-0.07529*x) -2.063e+005*exp(-0.07536 *x);
plot(x,y,'--',x,y3,'-o');
grid on;
5.
x=[0:1:4];
y=[44.48556623 54.5320405 59.79178874 69.03973939 72.15086514];y2=42.29 + 2.449 *cos(x*0.2749) + 32.61*sin(x*0.2749);
plot(x,y,'--',x,y2,'-o');
grid on;
6.
x=[0:1:9];
y7=42.29 + 2.449 *cos(x*0.2749) + 32.61*sin(x*0.2749);
y7
1.
x1=[0.455544275 0.541542453 0.595533854 0.682681875 0.724812977 ];
x2=[0.415468779 0.583256115 0.581482314 0.697288343 0.797434953 ];
x3=[0.489219269 0.515736684 0.583646355 0.661576338 0.749965397];
x4=[0.416962175 0.495571922 0.589116229 0.697595173 0.875468267];
y=[44.48557 54.53204 59.79179 69.03974 72.15087];
X=[ones(length(y),1),x1',x2',x3',x4'];
Y=y';
[b,bint,r,rint,stats]=regress(Y,X);
b,bint,r,rint,stats
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2013年认证杯SPSSPRO杯数学建模C题(第二阶段)公路运输业对于国内生产总值的影响分析全过程文档及程序
2013年认证杯SPSSPRO杯数学建模 C题 公路运输业对于国内生产总值的影响分析 原题再现: 交通运输作为国民经济的载体,沟通生产和消费,在经济发展中扮演着极其重要的角色。纵观几百年来交通运输与经济发展的相互关系,生产水平越高…...
)
《LeetCode力扣练习》代码随想录——二叉树(合并二叉树---Java)
《LeetCode力扣练习》代码随想录——二叉树(合并二叉树—Java) 刷题思路来源于 代码随想录 617. 合并二叉树 二叉树-前序遍历 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode…...

openstack云计算(二)——使用Packstack安装器安装一体化OpenStack云平台
初步掌握OpenStack快捷安装的方法。掌握OpenStack图形界面的基本操作。 一【准备阶段】 (1)准备一台能够安装OpenStack的实验用计算机,建议使用VMware虚拟机。 (2)该计算机应安装CentOS 7,建议采用CentO…...

Flutter Don‘t use ‘BuildContext‘s across async gaps.
Flutter提示Don‘t use ‘BuildContext‘s across async gaps.的解决办法—flutter里state的mounted属性...
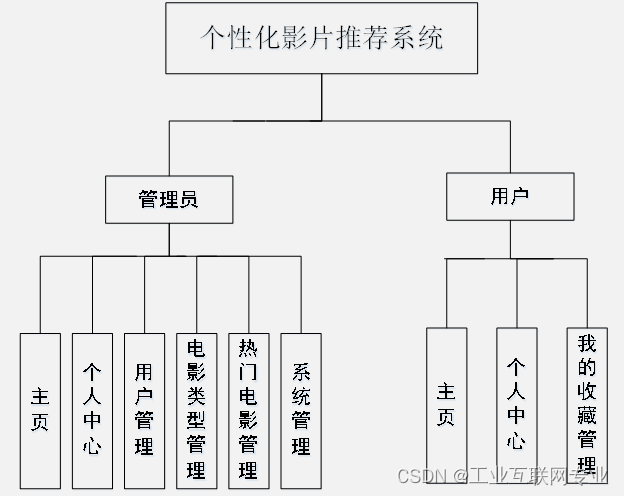
基于SSM+Jsp+Mysql的个性化影片推荐系统
开发语言:Java框架:ssm技术:JSPJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包…...
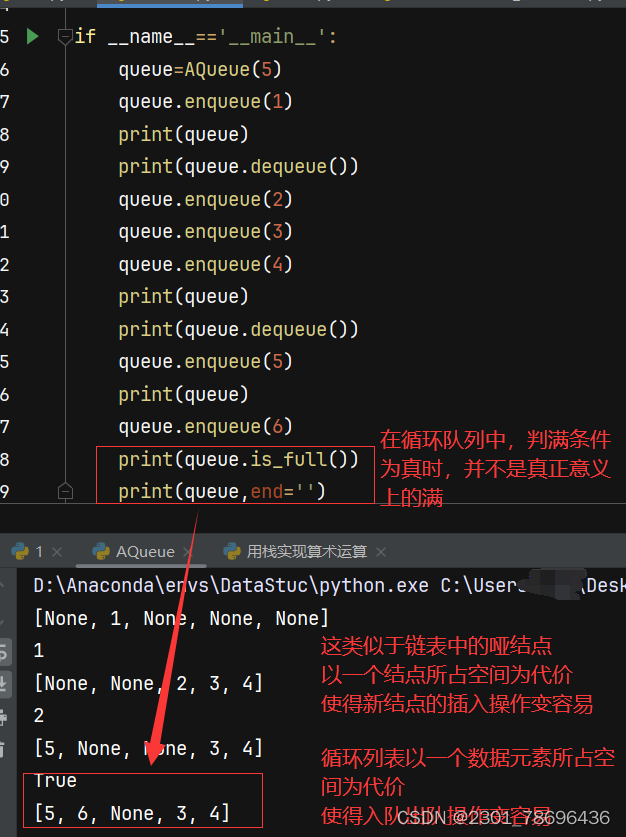
循环队列的实现及应用——桶排序bucket_sort、基数排序radix_sort
一、循环队列的实现 代码解释 1、完成初始化 2、定义方法 3、测试实例 4、完整代码 class AQueue:def __init__(self, size=10):self.__mSize = sizeself.__front=0self.__rear = 0self.__listArray = [None] * size#清空元素def clear(self):self.__front = 0self.__rear =…...

ubuntu16如何使用高版本cmake
1.引言 最近在尝试ubuntu16.04下编译开源项目vsome,发现使用apt命令默认安装cmake的的版本太低。如下 最终得知,ubuntu16默认安装确实只能到3.5.1。解决办法只能是源码安装更高版本。 2.源码下载3.20 //定位到opt目录 cd /opt 下载 wget https://cmak…...

电商-广告投放效果分析(KMeans聚类、数据分析-pyhton数据分析
电商-广告投放效果分析(KMeans聚类、数据分析) 文章目录 电商-广告投放效果分析(KMeans聚类、数据分析)项目介绍数据数据维度概况数据13个维度介绍 导入库,加载数据数据审查相关性分析数据处理建立模型聚类结果特征分析…...
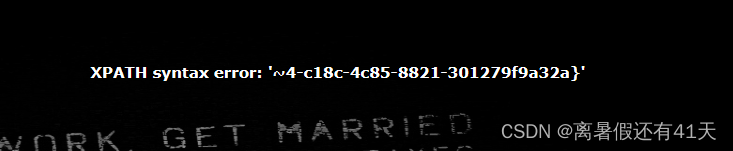
练习 16 Web [极客大挑战 2019]LoveSQL
extractvalue(1,concat(‘~’, (‘your sql’) ) )报错注入,注意爆破字段的时候表名有可能是table_name不是table_schema 有登录输入框 常规尝试一下 常规的万能密码,返回了一个“admin的密码”: Hello admin! Your password is…...
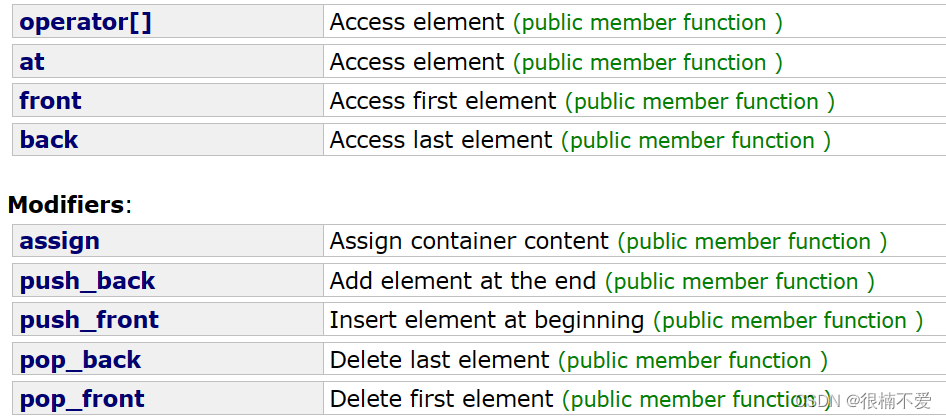
C++——栈和队列容器
前言:这篇文章我们将栈和队列两个容器放在一起进行分享,因为这两个要分享的知识较少,而且两者在结构上有很多相似之处,比如栈只能在栈顶操作,队列只能在队头和队尾操作。 不同于前边所分享的三种容器,这篇…...

Java集合(个人整理笔记)
目录 1. 常见的集合有哪些? 2. 线程安全的集合有哪些?线程不安全的呢? 3. Arraylist与 LinkedList 异同点? 4. ArrayList 与 Vector 区别? 5. Array 和 ArrayList 有什么区别?什么时候该应 Array而不是…...
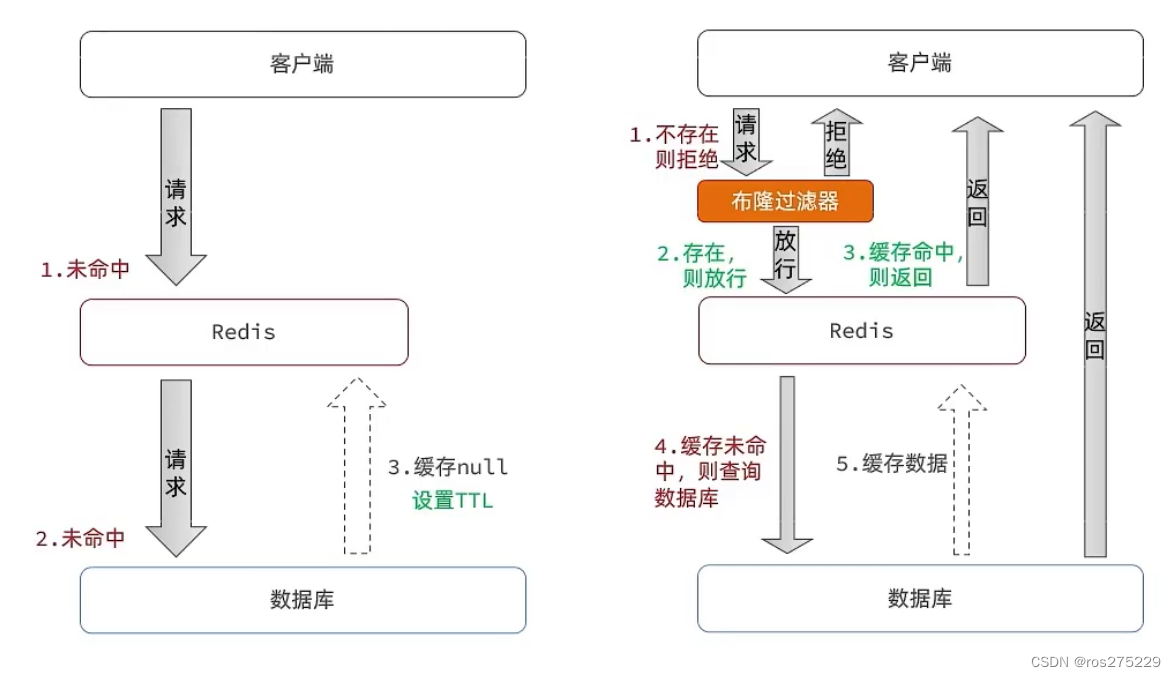
Redis -- 缓存穿透问题解决思路
缓存穿透 :缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,这样缓存永远不会生效,这些请求都会打到数据库。 常见的解决方案有两种: 缓存空对象 优点:实现简单,维护方便 缺点: 额外…...
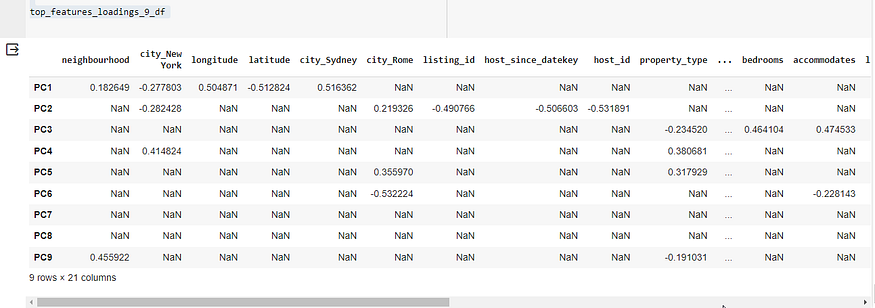
数据挖掘中的PCA和KMeans:Airbnb房源案例研究
目录 一、PCA简介 二、数据集概览 三、数据预处理步骤 四、PCA申请 五、KMeans 聚类 六、PCA成分分析 七、逆变换 八、质心分析 九、结论 十、深入探究 10.1 第 1 步:确定 PCA 组件的最佳数量 10.2 第 2 步:使用 9 个组件重做 PCA 10.3 解释 PCA 加载和特…...

【ArcGIS微课1000例】0107:ArcGIS加载在线历史影像服务WMTS
文章目录 一、WMTS历史影像介绍二、ArcGIS加载WMTS服务三、Globalmapper加载WMTS服务一、WMTS历史影像介绍 通过访问历史影响WMTS服务,可以将全球范围内历史影像加载进来,如下所示: WMTS服务: https://wayback.maptiles.arcgis.com/arcgis/rest/services/World_Imagery/WM…...

IP归属地在互联网行业中的应用
摘要:IP(Internet Protocol)地址归属地是指互联网上某个IP地址所对应的地理位置信息。在互联网行业中,IP归属地具有重要的应用价值,包括网络安全、广告定向、用户定位等方面。IP数据云将探讨IP归属地在互联网行业中的应…...

非关系型数据库-----------探索 Redis高可用 、持久化、性能管理
目录 一、Redis 高可用 1.1什么是高可用 1.2Redis的高可用技术 二、 Redis 持久化 2.1持久化的功能 2.2Redis 提供两种方式进行持久化 三、Redis 持久化之----------RDB 3.1触发条件 3.1.1手动触发 3.1.2自动触发 3.1.3其他自动触发机制 3.2执行流程 3.3启动时加载…...

每日一题:三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 1…...
【SCI绘图】【曲线图系列2 python】多类别标签对比的曲线图
SCI,CCF,EI及核心期刊绘图宝典,爆款持续更新,助力科研! 本期分享: 【SCI绘图】【曲线图系列2 python】多类别标签对比的曲线图,文末附完整代码。 1.环境准备 python 3 import proplot as pp…...
达梦DMHS-Manager工具安装部署
目录 1、前言 1.1、平台架构 1.2、平台原理 2、环境准备 2.1、硬件环境 2.2、软件环境 2.3、安装DMHS 2.3.1、源端DMHS前期准备 2.3.2、源端DMHS安装 2.3.3、目的端DMHS安装 3、DMHS-Manager客户端部署 3.1、启动dmhs web服务 3.2、登录web管理平台 4、添加DMHS实…...

Marketo营销自动化集成Zoho CRM
Marketo 本身是一种营销自动化工具,可让您根据指定的标准对潜在客户进行评分,并确定哪些潜在客户最有可能进行转化。 CRM 和 Marketo 之间的紧密集成可帮助您规划销售和营销活动,以培育这些高价值潜在客户并最大限度地提高您的团队可以赢得的…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
