【XCPC笔记】2023 (ICPC) Jiangxi Provincial Contest——ABCIJKL 做题记录
补题
赛后gym练习及补题,gym链接:2023 (ICPC) Jiangxi Provincial Contest – Official Contest
另外,D题我也打算找机会学习写下,C题的博弈论还需要好好理解,感觉都是比较有趣的数学问题
补题顺序如下
- 补题
- L [Zhang Fei Threading Needles - Thick with Fine](https://codeforces.com/gym/104385/problem/L)
- 题面解读
- 参考代码
- A [Drill Wood to Make Fire](https://codeforces.com/gym/104385/problem/A)
- 题面解读
- 参考代码
- B [Wonderful Array](https://codeforces.com/gym/104385/problem/B)
- 题面解读
- 参考代码
- I [Tree](https://codeforces.com/gym/104385/problem/I)
- 题面解读
- 参考代码
- J [Function](https://codeforces.com/gym/104385/problem/J)
- 题面解读
- 参考代码
- K [Split](https://codeforces.com/gym/104385/problem/K)
- 题面解读
- 参考代码
- C [Battle](https://codeforces.com/gym/104385/problem/C)
- 题面解读
- 参考代码
L Zhang Fei Threading Needles - Thick with Fine
签到题
题面解读
当时在场人数为N,其中夏侯杰被吓死了,其他人被吓跑了,请问张飞吓跑了的人数是多少?
输出N-1即可
参考代码
#include<bits/stdc++.h>
using namespace std;int main()
{ios::sync_with_stdio(0), cin.tie(0);int n; cin >> n;cout << n - 1;return 0;
}
A Drill Wood to Make Fire
签到题
题面解读
钻木取火与钻木的速度与力量有关,当速度与力量的乘积大于某个阈值的时候,能够钻木取火成功。提供阈值、力量、速度,问是否能够取火成功。
参考代码
#include<bits/stdc++.h>
using namespace std;
int n, s, v;int main()
{ios::sync_with_stdio(0), cin.tie(0);int t; cin >> t;while(t--){cin >> n >> s >> v;if(s * v >= n) cout << "1\n";else cout << "0\n";}return 0;
}
B Wonderful Array
数学题
题面解读
给定一个长度为 k 的数组 a ,对于长度为 n 的数组 b :
b i = { x , i = 0 b i − 1 + a i − 1 m o d k , 0 < i ≤ n b_{i}=\begin{cases}x,i=0\\ b_{i-1}+a_{i-1}\quad mod \quad k,0 <i\leq n\end{cases} bi={x,i=0bi−1+ai−1modk,0<i≤n
找出 有多少个 i 使得 :
b i m o d m ≤ b i + 1 m o d m b_{i} \quad mod \quad m\leq b_{i+1}\quad mod \quad m bimodm≤bi+1modm
此处,由于 a[i] 大于 0,所以 b[i] 在不取模情况下一定是一个单调递增的。所以正向考虑满足题意的部分,直接顺序枚举会是一个 O(n) 的复杂度,题目限制 1s ,这样肯定超时。
那么,我们选择反向考虑,寻找能够使得 b[i] > b[i + 1] (取模后)的位置。由于对 m 取模,那么对于一个递增的数组,这个位置就应该每当数组递增超过 m 就出现一次。在整个b数组过程中,就应该有 b[n]/m 个。那么新的问题就是如何去计算 b[n] ?由于 数组 b 一直在对 k 取模,所以 数组 b 是一个周期性增减的,我们就不用去看整个数组b而是找其中一段。计算 数组b[n] 的办法详见代码。
最终答案的个数是 n - b[n]/m。
参考代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int K = 1e6 + 5;ll k, n, m, x;
ll arr[K];int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> k;for(int i = 0; i < k; ++i) cin >> arr[i];cin >> n >> m >> x;ll b = 0, cnt = 0;x = x % m;for(int i = 0; i < k; ++i) b += arr[i] % m;b = n / k * b + x;for(int i = 0; i < n % k; ++i) b += arr[i] % m;cout << n - b / m;return 0;
}
I Tree
异或
题面解读
一个 n 节点的树,结点连接的边有边权。执行 q 次操作:
- 对结点
x到结点y的路径上每条边的边权异或z。 - 询问编号为
x的结点的所有边的边权异或和。
此处,有个小的脑筋急转弯。比如,对于操作1,如果1-2-3这三个点按照这个顺序连接,当让1到3的路径上边权都异或上 w ,那么此时对于结点 2 ,它所连接的两个边的异或和是没有变化的:比如 1与2的边权为 3 ,2 与 3 的边权大小为 5,对结点 1 到结点 2 的路径上每条边的边权异或 2 ,对于结点2的边权异或和 3 ^ 5 ==> 3 ^ 2 ^ 5 ^ 2 == 3 ^ 5,因为对于一个数异或自己为0。
那么,操作1的修改只会对 x 和 y 有效。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, q, v[N];
int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n >> q;for(int i = 1; i <= n - 1; ++i){int x, y, w;cin >> x >> y >> w;v[x] ^= w, v[y] ^= w;}while(q--){int op; cin >> op;if(op == 1){int x, y, z;cin >> x >> y >> z;v[x] ^= z, v[y] ^= z;}else{int x; cin >> x;cout << v[x] << '\n';}}return 0;
}
J Function
题面解读
给定多个一元二次函数,询问在某一点处的最小值是多少。
当给出一个一元二次函数的时候,我们就可以去通过这个函数去更新其他点上最小值是多少。而如果我们每给出一个函数,就去更新 1 ~ n 上所有点的话,最坏的时间复杂度就是 O(1e10),无法在1s 内跑完。
根据题目中 b b b 的数据范围肯定小于 1e5 ,那么当
( x − i ) 2 > b \left( x-i\right) ^{2} >b (x−i)2>b
此时就不用再去维护这个最小值,因为肯定大于其他函数在这个位置上的最小值。
参考代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;ll arr[N], a, b;
int n, m;
int mxl = int(sqrt(1e5) + 0.5); // 向上取整,大概317void update(int x)
{arr[x] = min(arr[x], b);for(int i = x - 1, j = 1; i >= 1 && j <= mxl; ++j, --i)arr[i] = min(arr[i], j * j + b);for(int i = x + 1, j = 1; i <= n && j <= mxl; ++j, ++i)arr[i] = min(arr[i], j * j + b);
}int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n;memset(arr, 0x3f, sizeof arr);for(int i = 1; i <= n; ++i){cin >> b;update(i);}cin >> m;for(int i = 1; i <= m; ++i){int op; cin >> op;if(op){cin >> a; cout << arr[a] << "\n";}else{cin >> a >> b;update(a);}}return 0;
}
K Split
题面解读
题目中给出了一个长度为 n n n 的非增序列。进行 m m m 次操作,分为两种:
操作0,给你一个 1 < x < n 1 <x <n 1<x<n ,使得 a x = a x + 1 + a x − 1 − a x a_{x}=a_{x+1}+a_{x-1}-a_{x} ax=ax+1+ax−1−ax
操作1,将序列分成 k k k 个小块,其中每个小块的最大值-最小值之和要最小,并且输出每个小块中最大值-最小值之和最小值。
对于操作1,随机挑选一段,结果为: a 1 − a i + a i + 1 − . . . − a j + a j + 1 − a n a_1 - a_i + a_{i+1} -... - a_j + a_{j+1} - a_n a1−ai+ai+1−...−aj+aj+1−an, 整理后得: a 1 − a n + a i + 1 − a i + a j + 1 − a j . . . a_1 - a_n + a_{i+1} - a_i + a_{j+1} - a_j ... a1−an+ai+1−ai+aj+1−aj...。可以看出,前两项一定且大于0,后面每两项都是相邻两数之差且小于等于0(后一项-前一项)。因此,为了让最大值减最小值之和最小,我们挑选这个序列中最小的 k − 1 k-1 k−1 个差就可以了。
对于操作0,对序列中某段 a x − 1 , a x , a x + 1 a_{x-1},a_x,a_{x+1} ax−1,ax,ax+1,转变为 a x − 1 , a x + 1 + a x − 1 − a x , a x + 1 a_{x-1},a_{x+1}+a_{x-1}-a_{x},a_{x+1} ax−1,ax+1+ax−1−ax,ax+1。
对于初始情况,这一段的后一项-前一项为: a x − a x − 1 , a x + 1 − a x a_x - a_{x-1},a_{x+1}-a_x ax−ax−1,ax+1−ax,改变之后为: a x − 1 − a x , a x − a x + 1 a_{x-1}-a{x},a_{x}-a_{x+1} ax−1−ax,ax−ax+1。可见,这一波操作并没有对整个序列的差分造成什么影响。所以后续代码中也不会对操作0进行任何处理。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
int n, m;
ll a[N], b[N];int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n;for(int i = 0; i < n; ++i) cin >> a[i];for(int i = 1; i < n; i++) b[i] = a[i] - a[i - 1]; // 计算上述后项与前项的差sort(b + 1, b + n); // 将差分结果排序for(int i = 1; i < n; i++) b[i] = b[i] + b[i - 1]; // 将排序完的结果计算前缀和,方便后续查询直接使用cin >> m;while(m--){int op, k;cin >> op >> k;if(op == 1) cout << a[0] - a[n - 1] + b[k - 1] << "\n"; // 只要选择前 K-1 项即可}return 0;
}
C Battle
题面解读
博弈论中一个经典的Nim游戏,为了补题,专门去看了一眼什么是公平组合游戏。虽然看了,感觉明白了但没完全明白,感兴趣的可以去看看大佬的博客,本蒟蒻还得再吸收理解几遍。
推荐参考理解的博客:算法学习笔记(51): SG函数 、公平组合游戏
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll p, ans;ll sg(ll x)
{if(x == p) return 2;if(x&1) return 1;return 0;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cin >> n >> p;for (int i = 0; i < n; i++){ll t;cin >> t;if (p & 1){if(t&1) ans ^= 1;else ans ^= 0;}else{ans ^= sg(t % (p + 1));}}if(ans) cout << "GOOD\n";else cout << "BAD\n";return 0;
}
相关文章:
 Jiangxi Provincial Contest——ABCIJKL 做题记录)
【XCPC笔记】2023 (ICPC) Jiangxi Provincial Contest——ABCIJKL 做题记录
补题 赛后gym练习及补题,gym链接:2023 (ICPC) Jiangxi Provincial Contest – Official Contest 另外,D题我也打算找机会学习写下,C题的博弈论还需要好好理解,感觉都是比较有趣的数学问题 补题顺序如下 补题L [Zhang …...

猫头虎分享已解决Bug || **URLError (URL错误)** 全方位解析
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...
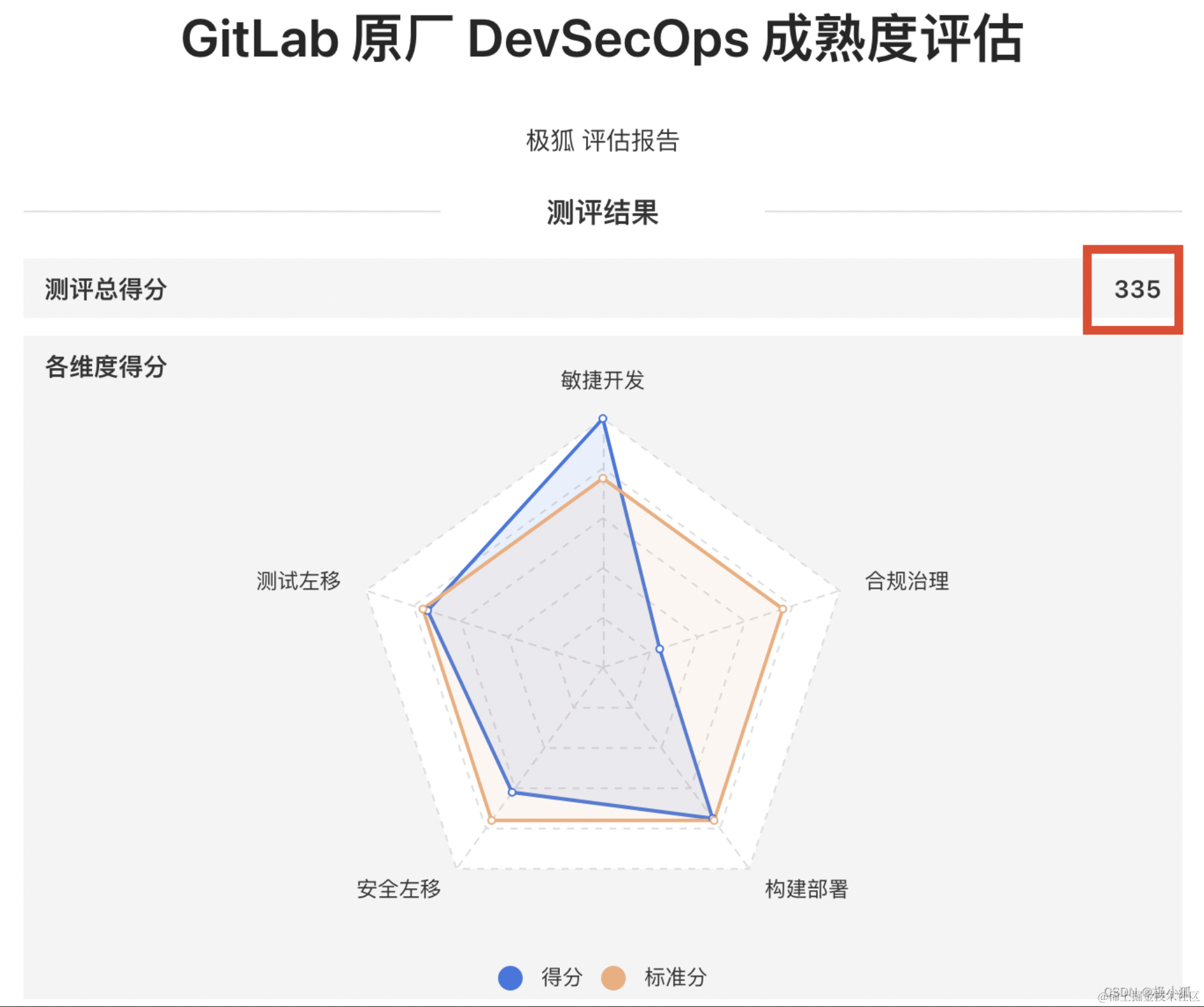
如何使用极狐GitLab 启用自动备份功能
本文作者:徐晓伟 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 本文主要讲述了如何极狐GitLab 自…...

HTML/XML转义字符对照
特殊字符转义表 字符十进制转义字符""&&<<<>>>不断开空格(non-breaking space) 最常用的转义字符列表 显示说明实体名称十进制编号半方大的空白 全方大的空白 不断行的空白格 <小于<<>大于&g…...

设计模式:组合模式示例
组合模式的典型例子通常涉及到树形结构的处理,下面是几个形象且易于理解的例子: 文件系统 在文件系统中,目录可以包含文件或者其他目录,但是从用户的角度来看,目录和文件都可以被“打开”或者“获取大小”。这里的目…...
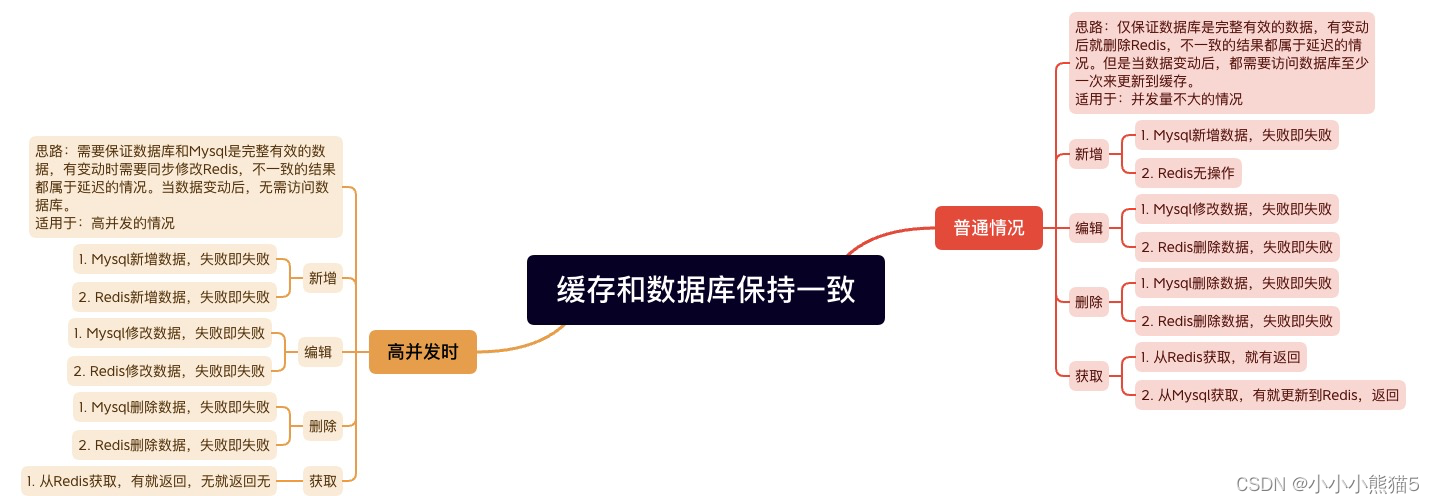
普通情况和高并发时,Redis缓存和数据库怎么保持一致?
普通情况和高并发时,Redis缓存和数据库怎么保持一致? 普通情况思路 高并发时思路 Q:缓存和数据库怎么保持一致? A:绝对不可能保持一致的,在实际业务开发中,有一些方案可以做取舍。 实际业务中&a…...

Django -- 自动化测试
概述 测试是一种例行的、不可缺失的工作,用于检查你的程序是否符合预期。 测试可以划分为不同的级别。一些测试可能专注于小细节(比如某一个模型的方法是否会返回预期的值?), 一些测试则专注于检查软件的整体运行是否…...

NodeJS 在Windows / Mac 上实现多版本控制
NodeJS 的多版本控制 本文介绍一下在 windows/MacOS 上 如何 切换和使用多个版本的 NodeJS。 Windows 本小节介绍一下在windows上管理不同版本的NodeJS。 nvm-windows 工具 nvm-windows 是在 windows 上管理 NodeJS 版本的一个工具。 它可以很方便的 下载、移除、查看、切…...

Web3 游戏周报(3.24-3.30)
【3.24-3.30】Web3 游戏行业动态: Web3 开发平台 Mirror World 在 Solana 上推出首个游戏 rollup 链 NFT 卡牌游戏 Parallel 完成 3,500 万美元融资,Solana Ventures 等参投 加密游戏开发公司 Gunzilla Games 完成 3,000 万美元融资 Telegram 游戏 No…...

算法思想1. 分治法2. 动态规划法3. 贪心算法4. 回溯法
目录 递归和动态的区别:空间和时间复杂度之争 递归空间复杂度低;动态时间复杂度第低...
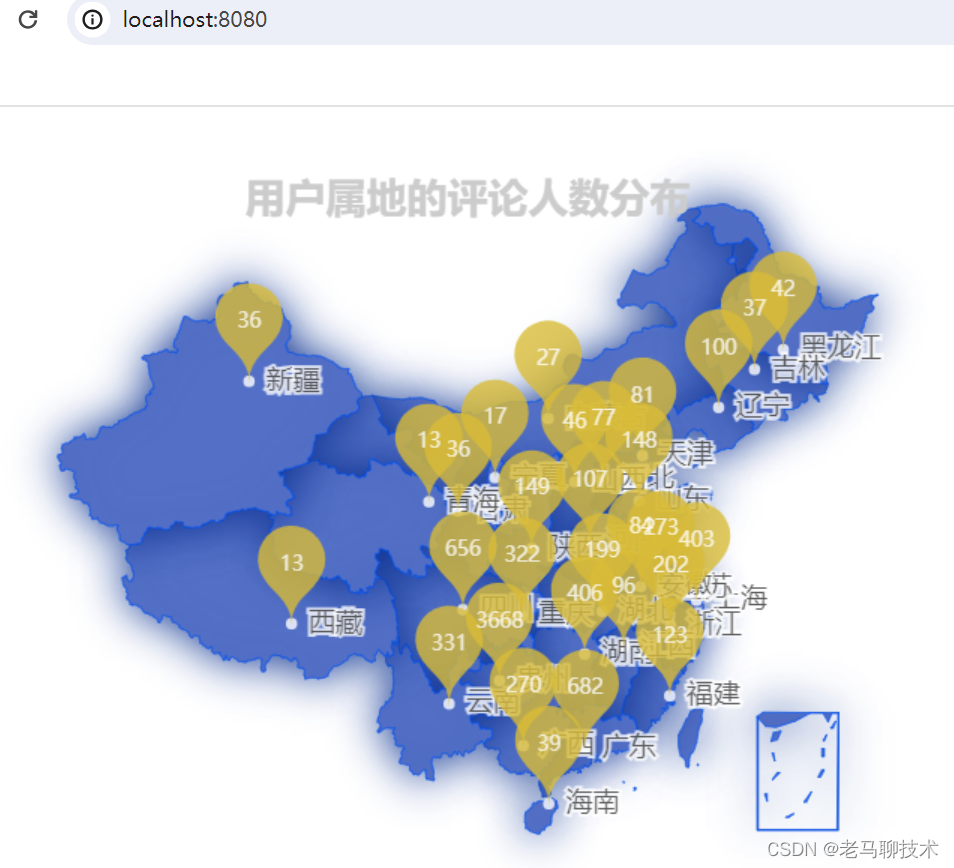
SpringBoot+ECharts+Html 地图案例详解
1. 技术点 SpringBoot、MyBatis、thymeleaf、MySQL、ECharts 等 此案例使用的地图是在ECharts社区中查找的:makeapie echarts社区图表可视化案例 2. 准备条件 在mysql中创建数据库echartsdb,数据库中创建表t_location_count表,表中设置两个…...

达梦数据库 优化
谁进行优化?优化什么? 优化不能仅从数据库方面考虑,比如,在存储达到数据库极限、应用涉及人员设计的代码稀巴烂的情况下,进行调优就是杯水车薪的效果。 涉及到优化人员: 数据库管理员应用程序架构师应用…...
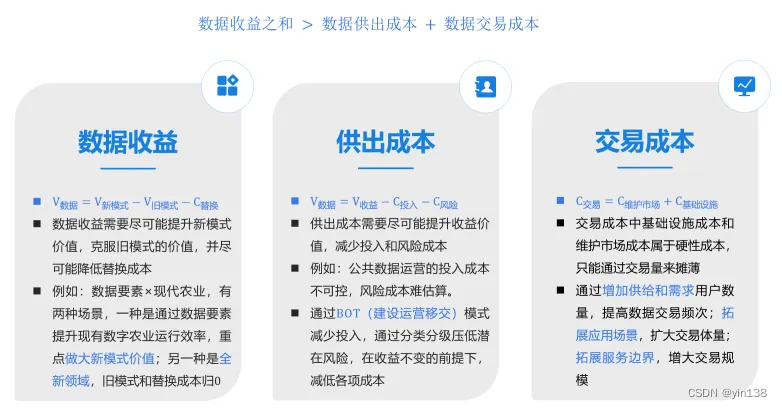
数据如何才能供得出、流得动、用得好、还安全
众所周知,数据要素已经列入基本生产要素,同时成立国家数据局进行工作统筹。目前数据要素如何发挥其价值,全国掀起了一浪一浪的热潮。 随着国外大语言模型的袭来,国内在大语言模型领域的应用也大放异彩,与此同时&#x…...
idea开发 java web 酒店推荐系统bootstrap框架开发协同过滤算法web结构java编程计算机网页
一、源码特点 java 酒店推荐推荐系统是一套完善的完整信息系统,结合java web开发和bootstrap UI框架完成本系统 采用协同过滤算法进行推荐 ,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式…...
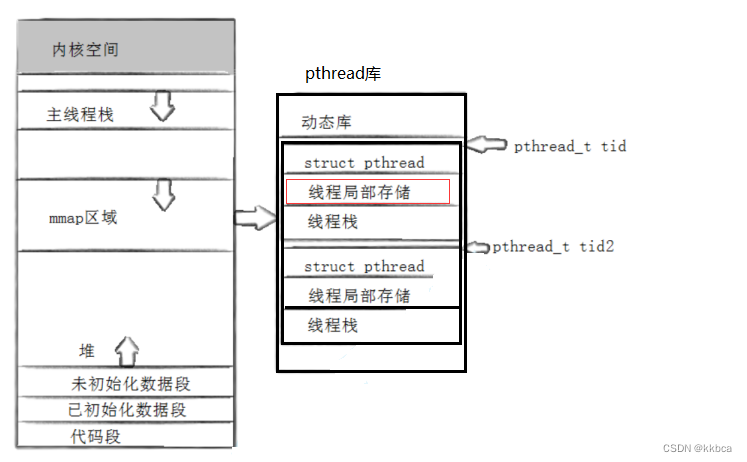
Linux——线程控制
目录 前言 一、线程创建 1.创建线程 2.线程传递结构体 3.创建多线程 4.收到信号的线程 二、线程终止 三、线程等待 四、线程分离 五、取消线程 六、线程库管理的原理 七、站在语言角度理解pthread库 八、线程的局部存储 前言 前面我们学习了线程概念和线程创建&…...

【Leetcode 347】,前k个高频元素,小根堆的调整
参考题解 题目:给定一个数组,输出 前k个高频元素。 思路: 遍历数组,建立小根堆(小根堆的元素是元组(num,freq),排序规则是每个元素的频率)。 下面使用数组‘heap’&…...

【图论】【分类讨论】LeetCode3017按距离统计房屋对数目
本文涉及的知识点 图论 分类讨论 本题同解 【差分数组】【图论】【分类讨论】【整除以2】3017按距离统计房屋对数目 LeetCode3017按距离统计房屋对数目 给你三个 正整数 n 、x 和 y 。 在城市中,存在编号从 1 到 n 的房屋,由 n 条街道相连。对所有 …...

浅谈Yum 安装和 源码安装
浅谈Yum 安装和 源码安装 本文所叙述的Linux系统是基于RedHat发行版的CentOS7 yum安装 1. 前言 我们知道在Windows上下载的安装包后缀是 .exe ,与之对应的 在 Linux下的安装包的后缀是 .rpm rpm (Red Hat Package Manager) 是红帽软件包管理器 我们在Windows电脑…...
)
JavaEE初阶Day 3:多线程(1)
目录 Day 3:多线程(1)1. 线程1.1 引入线程的原因1.2 线程的定义1.3 为何线程更轻量1.4 问题 2. 多线程代码2.1 继承Thread重写run2.2 通过实现Runnable接口创建线程2.3 针对2.1的变形使用匿名内部类2.4 针对Runnable创建匿名内部类2.5 使用la…...

gutil140.dll是什么?gutil140.dll无法继续执行的解决方法
gutil140.dll文件是一个动态链接库(DLL)文件,通常与Microsoft Visual Studio 2015相关联。 gutil140.dll是开发过程中使用的工具函数集合,它辅助开发人员执行常见的编程任务,如文件操作、内存分配和字符串处理等。这个…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
