【图论】【分类讨论】LeetCode3017按距离统计房屋对数目
本文涉及的知识点
图论 分类讨论
本题同解
【差分数组】【图论】【分类讨论】【整除以2】3017按距离统计房屋对数目
LeetCode3017按距离统计房屋对数目
给你三个 正整数 n 、x 和 y 。
在城市中,存在编号从 1 到 n 的房屋,由 n 条街道相连。对所有 1 <= i < n ,都存在一条街道连接编号为 i 的房屋与编号为 i + 1 的房屋。另存在一条街道连接编号为 x 的房屋与编号为 y 的房屋。
对于每个 k(1 <= k <= n),你需要找出所有满足要求的 房屋对 [house1, house2] ,即从 house1 到 house2 需要经过的 最少 街道数为 k 。
返回一个下标从 1 开始且长度为 n 的数组 result ,其中 result[k] 表示所有满足要求的房屋对的数量,即从一个房屋到另一个房屋需要经过的 最少 街道数为 k 。
注意,x 与 y 可以 相等 。
示例 1:
输入:n = 3, x = 1, y = 3
输出:[6,0,0]
解释:让我们检视每个房屋对
- 对于房屋对 (1, 2),可以直接从房屋 1 到房屋 2。
- 对于房屋对 (2, 1),可以直接从房屋 2 到房屋 1。
- 对于房屋对 (1, 3),可以直接从房屋 1 到房屋 3。
- 对于房屋对 (3, 1),可以直接从房屋 3 到房屋 1。
- 对于房屋对 (2, 3),可以直接从房屋 2 到房屋 3。
- 对于房屋对 (3, 2),可以直接从房屋 3 到房屋 2。
示例 2:
输入:n = 5, x = 2, y = 4
输出:[10,8,2,0,0]
解释:对于每个距离 k ,满足要求的房屋对如下: - 对于 k == 1,满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 4), (4, 3), (4, 5), 以及 (5, 4)。
- 对于 k == 2,满足要求的房屋对有 (1, 3), (3, 1), (1, 4), (4, 1), (2, 5), (5, 2), (3, 5), 以及 (5, 3)。
- 对于 k == 3,满足要求的房屋对有 (1, 5),以及 (5, 1) 。
- 对于 k == 4 和 k == 5,不存在满足要求的房屋对。
示例 3:
输入:n = 4, x = 1, y = 1
输出:[6,4,2,0]
解释:对于每个距离 k ,满足要求的房屋对如下: - 对于 k == 1,满足要求的房屋对有 (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), 以及 (4, 3)。
- 对于 k == 2,满足要求的房屋对有 (1, 3), (3, 1), (2, 4), 以及 (4, 2)。
- 对于 k == 3,满足要求的房屋对有 (1, 4), 以及 (4, 1)。
- 对于 k == 4,不存在满足要求的房屋对。
分类讨论
假定x != y
不失一般性,令x < y。
则x ↔ \leftrightarrow ↔ y ,是环。房屋z1和z2,令z1 < z2 分类如下:
分类一,z1 < x ,z2 < x 。则两者经过的街道数为z2-z1。
分类二,z1,z2 ∈ \in ∈[x,y] 。min(z2-z1,y-z2+z1-x+1)。
分类三:z1,z2 > y。和分类一类似。
分类四:z1 < x ,z2 ∈ \in ∈[x,y]。 min(z2-z1,y-z2+1+(x-z1))
分类五:z1 < x ,z2 > y 。则两者经过的街道数为(z1-x)+1+(z2-y)。通过x,y中中转多花 x+1-y ,由于y > x,故多化的<=0,更优。
分类六:z1 ∈ \in ∈[x,y],z2 > y。 min(z2-z1,z1-x+1+(z2-y))
总结后的分类
新分类一:[z3,z4] 都不通过x ↔ \leftrightarrow ↔y 中转。包括分类一,分类五,及x==y。
距离为1的数量为:z4-z3。
距离为2的数量为:z4-z3-1
⋮ \vdots ⋮
新分类二:两个点都在环上,环的长度为len。则两点的合法距离只能 ∈ \in ∈[1,len/2] 原分类二。
如果len是偶数,距离len/2的点对数量为len/2,z5 → \rightarrow →z6 就是 z6 → \rightarrow →z5。
其它情况点对数量为:len。
新分类三:两个点分别在环两侧。分类五。
长度为3的点对:1。
长度为4的点对:2。
长度为5的点对:3 。
令环左侧的点数为len1,环右侧的点数为len2。计算距离为d的数量:
minl = max(0,d-3-(len2-1))
maxl = min(len1-1,d-3)
距离为d的点对数量:maxl - minl +1 。
新分类四:环上一点,一侧一点。原分类四六。
把环拆成两个,就和新分类三基本一致。

拆分成{2,1,4}和{5,6},同时拆分成{3,4} {5,6}
交点4 被计算了两次,要扣掉。
代码
核心代码
class Solution {
public:vector<long long> countOfPairs(int n, int x, int y) {m_vRet.resize(n);if (x == y) {Do1(1, n);return m_vRet;}if (x > y) {swap(x, y);}Do1(1, x - 1);const int iCycLen = y - x + 1;Do2(iCycLen);Do1(y + 1, n);Do4(iCycLen, x - 1);Do3(x - 1, 3, n - y);Do4(iCycLen, n - y);return m_vRet;}void Do1(int left, int r){for (int d = 1; d <= r - left; d++) {update(d, r - left + 1 - d);}}void Do2(int iCycLen){for (int d = 1; d <= iCycLen / 2; d++){const int cnt = ((0 == iCycLen % 2) && (iCycLen / 2 == d)) ? iCycLen / 2 : iCycLen;update(d, cnt);}}void Do3(int len1, int iMidDis, int len2){for (int d = 0; d <= len1 + len2 - 2; d++){const int minl = max(0, d - (len2 - 1));const int maxl = min(len1 - 1, d);update(d + iMidDis, maxl - minl + 1);}}void Do4(int iCycLen, int len){Do3((iCycLen+1) / 2 , 1, len);Do3(iCycLen / 2 + 1, 1, len);for (int d = 1; d <= len; d++) {update(d, -1);}}inline void update(int d, int cnt){m_vRet[d - 1] += cnt*2;}vector<long long> m_vRet;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{int n, x, y;{Solution sln;n = 6, x = 1, y = 5;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{ 12, 14, 4, 0, 0, 0 });}{Solution sln;n = 3, x = 2, y = 2;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{4, 2, 0});}{Solution sln;n = 4, x = 1, y = 1;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{6, 4, 2, 0});}{Solution sln;n = 5, x = 2, y = 4;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{10, 8, 2, 0, 0});}{Solution sln;n = 3, x = 1, y = 3;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{6, 0, 0});}{Solution sln;n = 2, x = 2, y = 2;auto res = sln.countOfPairs(n, x, y);Assert(res, vector<long long>{2, 0});}
}

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【图论】【分类讨论】LeetCode3017按距离统计房屋对数目
本文涉及的知识点 图论 分类讨论 本题同解 【差分数组】【图论】【分类讨论】【整除以2】3017按距离统计房屋对数目 LeetCode3017按距离统计房屋对数目 给你三个 正整数 n 、x 和 y 。 在城市中,存在编号从 1 到 n 的房屋,由 n 条街道相连。对所有 …...

浅谈Yum 安装和 源码安装
浅谈Yum 安装和 源码安装 本文所叙述的Linux系统是基于RedHat发行版的CentOS7 yum安装 1. 前言 我们知道在Windows上下载的安装包后缀是 .exe ,与之对应的 在 Linux下的安装包的后缀是 .rpm rpm (Red Hat Package Manager) 是红帽软件包管理器 我们在Windows电脑…...
)
JavaEE初阶Day 3:多线程(1)
目录 Day 3:多线程(1)1. 线程1.1 引入线程的原因1.2 线程的定义1.3 为何线程更轻量1.4 问题 2. 多线程代码2.1 继承Thread重写run2.2 通过实现Runnable接口创建线程2.3 针对2.1的变形使用匿名内部类2.4 针对Runnable创建匿名内部类2.5 使用la…...

gutil140.dll是什么?gutil140.dll无法继续执行的解决方法
gutil140.dll文件是一个动态链接库(DLL)文件,通常与Microsoft Visual Studio 2015相关联。 gutil140.dll是开发过程中使用的工具函数集合,它辅助开发人员执行常见的编程任务,如文件操作、内存分配和字符串处理等。这个…...

在CentOS 7上安装Python 3.7.7
文章目录 一、实战步骤1. 安装编译工具2. 下载Python 3.7.7安装包3. 上传Python 3.7.7安装包4. 解压缩安装包5. 切换目录并编译安装6. 配置Python环境变量7. 使配置生效8. 验证安装是否成功 二、实战总结 一、实战步骤 1. 安装编译工具 在终端中执行以下命令 yum -y groupin…...
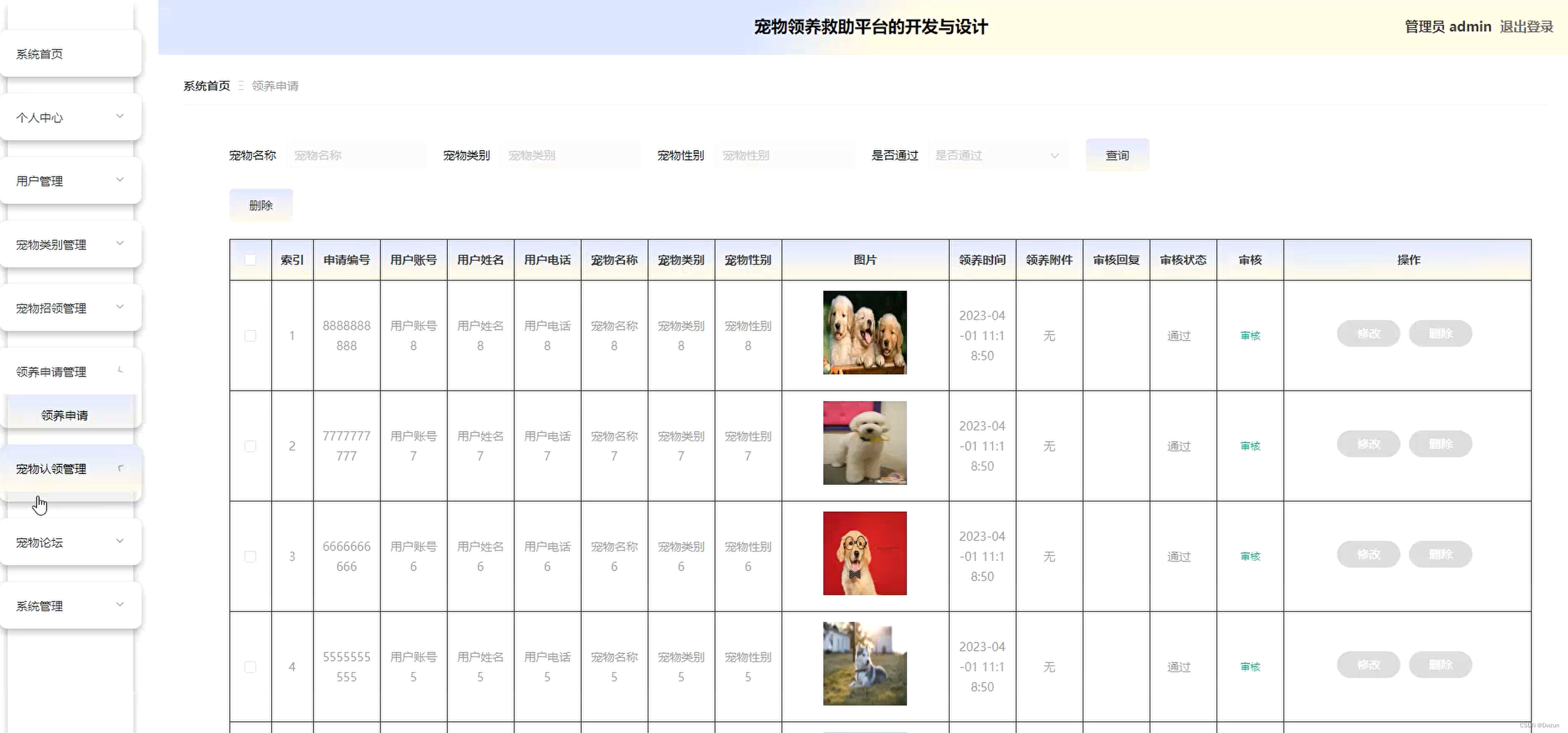
基于SpringBoot Vue宠物领养系统
一、📝功能介绍 基于SpringBoot Vue宠物领养系统 角色:管理员、用户 当游客打开系统的网址后,首先看到的就是首页界面。在这里,游客能够看到宠物领养救助平台的导航条显示首页、宠物招领、宠物认领、 宠物论坛、宠物资讯、后台管…...

ip命令
ip a 也是ip addr简写 [rootlocalhost ~]# ip a 1: lo: <LOOPBACK,UP,LOWER_UP> mtu 65536 qdisc noqueue state UNKNOWN group default qlen 1000link/loopback 00:00:00:00:00:00 brd 00:00:00:00:00:00inet 127.0.0.1/8 scope host lovalid_lft forever preferred_lft…...

【Kaggle】练习赛《鲍鱼年龄预测》(上)
前言 上一篇文章,讲解了《肥胖风险的多类别预测》机器学习方面的文章,主要是多分类算法的运用,本文是一个回归的算法,本期是2024年4月份的题目《Regression with an Abalone Dataset》即《鲍鱼年龄预测》,在此分享高手…...
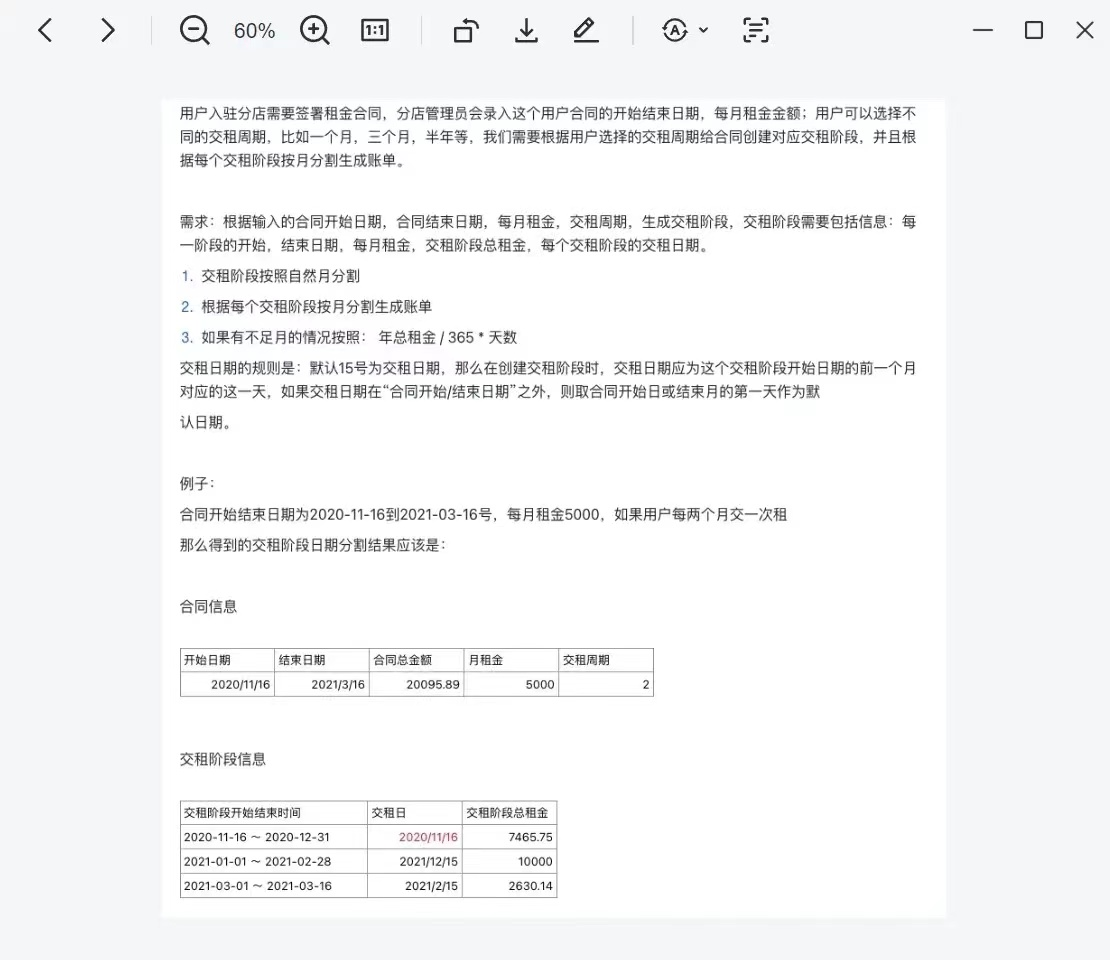
Ruby 之交租阶段信息生成
题目 我看了一下,这个题目应该不是什么机密,所以先放上来了。大概意思是根据合同信息生成交租阶段信息。 解答 要求是要使用 Ruby 生成交租阶段信息,由于时间比较仓促,变量名那些就用得随意了些。要点主要有下面这些:…...
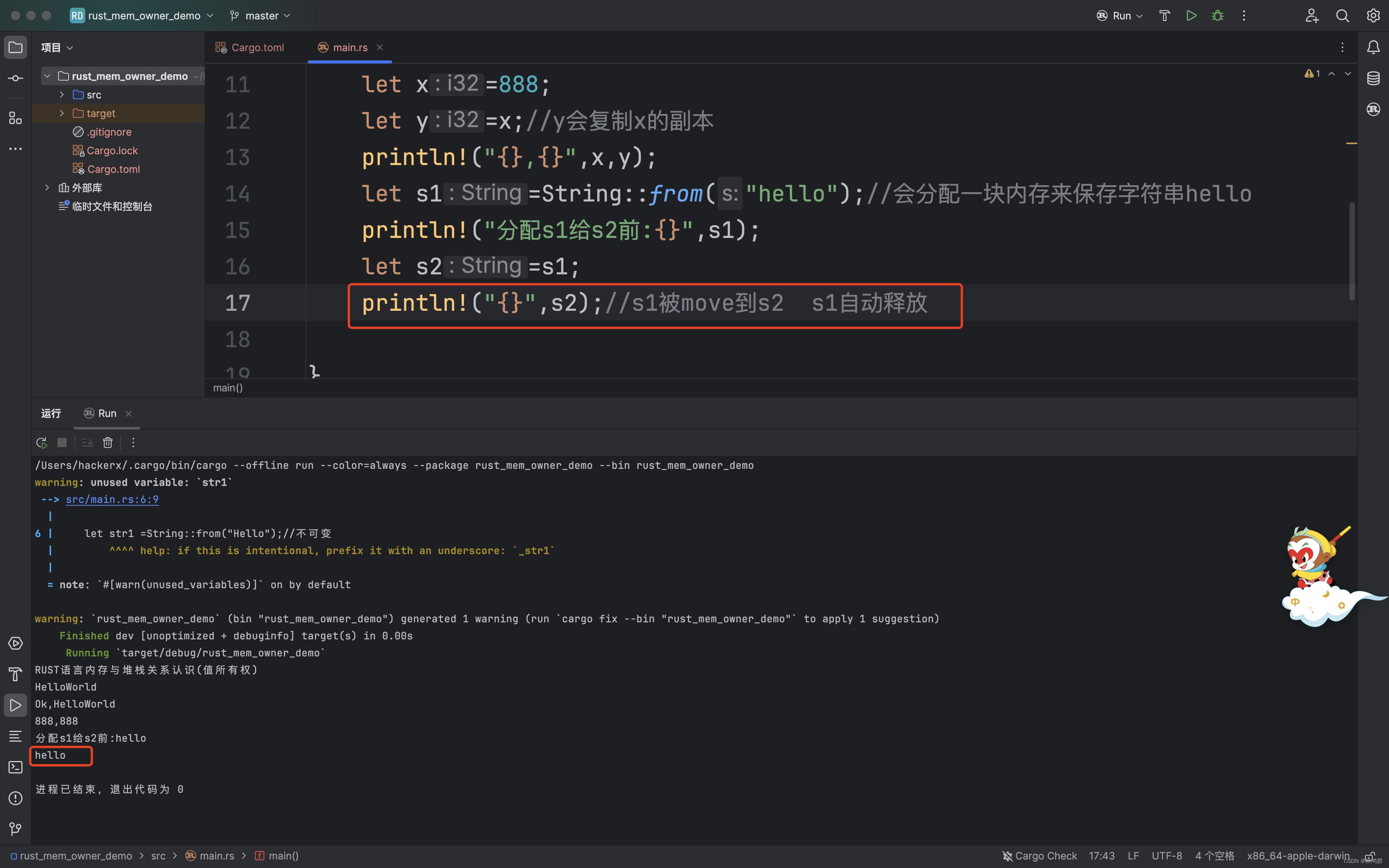
RUST语言值所有权之内存复制与移动
1.RUST中每个值都有一个所有者,每次只能有一个所有者 String::from函数会为字符串hello分配一块内存 内存示例如下: 在内存分配前调用s1正常输出 在分配s1给s2后调用报错 因为s1分配给s2后,s1的指向自动失效 s1被move到s2 s1自动释放 字符串克隆使用...
【Django学习笔记(三)】BootStrap介绍
BootStrap介绍 前言正文1、BootStrap 快速了解2、初识BootStrap2.1 下载地址2.2 创建目录2.3 引入BootStrap2.4 使用BootStrap 3、BootStrap 组件&样式3.1 导航条3.2 栅格系统3.3 container3.3.1 container3.3.2 container-fluid 3.4 面板3.5 媒体对象3.6 分页3.7 图标3.7.…...
)
ClickHouse开发相关(UDAF)
ClickHouse开发相关(UDAF) ClickHouse介绍 ClickHouse是一个开源、高性能的列式 OLAP 数据库管理系统,用于使用 SQL 进行实时分析。 为什么需要ClickHouse UDAF? ClickHouse中已存在了许多聚合函数,绝大多数情况下已经覆盖我们的需求,但是有时候我们仍然需要自定义函数…...
MySql并发事务问题
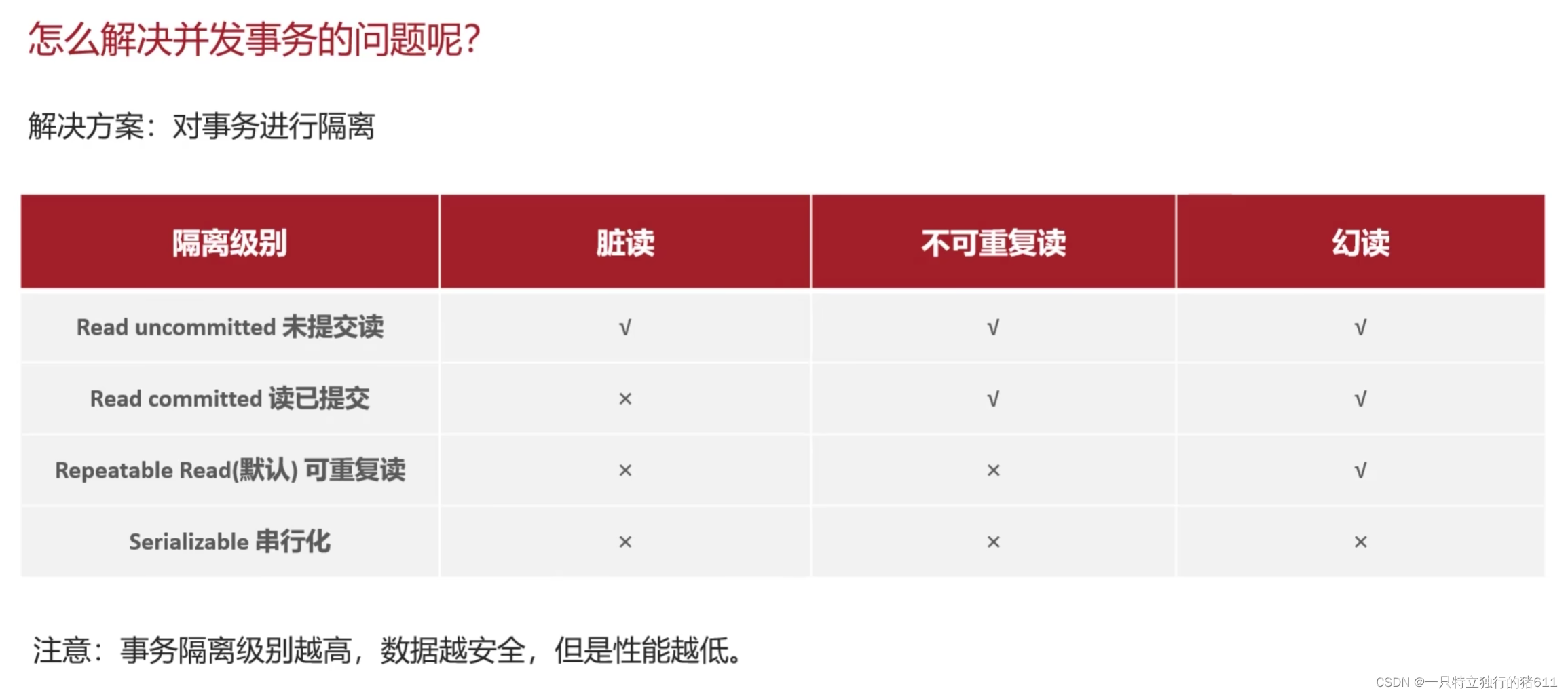
事务 事务概念: 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 事务的特性:ACID: 小…...

Windows下Docker创建Mysql5.7
安装 下载镜像,注意,要带版本号 docker pull mysql:5.7 等下载完成执行命令: 错误命令1,直接Windows下路径: docker run --name mysql57 --restartalways -p 3306:3306 -v F:/mysqldata/data57/log:/var/log/mysql…...
Redis(性能管理、主从复制、哨兵模式)概述及部署
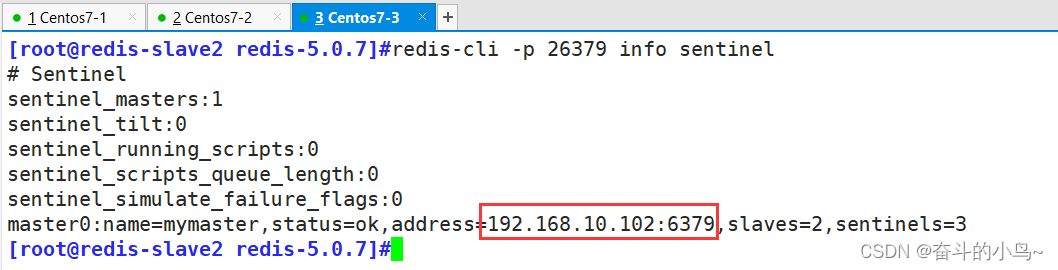
目录 一、性能管理 1、查看Redis内存使用 2、内存碎片率 3、跟踪内存碎片率 4、内存使用率 5、内回收key 二、Redis集群有三种模式 三、Redis主从复制 1、主从复制的概念 2、主从复制的作用 3、主从复制的流程 4、搭建Redis主从复制 1.环境准备 2.安装Redis&#…...
LabVIEW挖坑指南
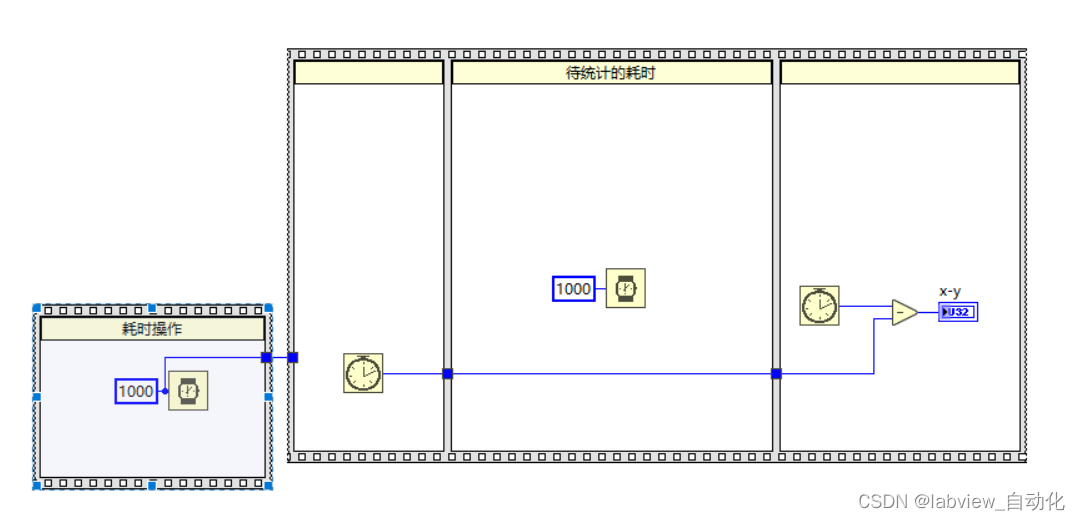
一、挖坑指南 1.1、输出变量放在条件框内 错误写法: 现象:如果没进入对应的分支,输出为默认值 正常写法: 让每个分支输出的值都在预料之内。 1.2、统计耗时不准 错误写法 现象:统计出来的耗时是2000ms 正常写法&a…...

docker容器环境安装记录(MAC M1)(完善中)
0、背景 在MAC M1中搭建商城项目环境时,采用docker统一管理开发工具,期间碰到了许多环境安装问题,做个总结。 1、安装redis 在宿主机新建redis.conf文件运行创建容器命令,进行容器创建、端口映射、文件挂载、以指定配置文件启动…...
Linux 常用命令(持续更新中...)
1. ls 查看文件列表命令 语法: ls [-a -l -h] [Linux路径] -a -l -h 是可选的选项 (-h需配合-l命令一起使用)Linux路径是此命令可选的参数 ls #查看当前目录所有非隐藏文件(平铺方式显示) ls -a #查看当前目录下所有文件 …...

xss.pwnfunction-Jefff
在eval中可以直接执行命令所以直接把"直接闭合在结尾再加上一个"因为后面的"没闭和会报错 ?jeffa";alert(1);" 或 ?jeffa"-alert(1)-" -是分隔符...
java——文件上传
一、文件上传——简介 文件上传的简介:文件上传是指将本地计算机中的文件传输到网络上的服务器或另一台计算机上的过程。在 Web 开发中,文件上传通常指的是将用户通过 Web 页面提交的文件(如图像、文档、音频、视频等)传输到服务器…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
