java数据结构与算法刷题-----LeetCode172. 阶乘后的零
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
文章目录
- 数学:阶乘的10因子个数
- 数学优化:思路转变为求5的倍数的个数
数学:阶乘的10因子个数
| 解题思路:时间复杂度O( n n n),n为5的个数,空间复杂度O( 1 1 1) |
|---|
- 如果想要求出阶乘,一定会超时。所以我们要找到破题点。就是什么条件下阶乘末尾会出现0。
- 我们发现阶乘结果求出来后,不断的提出因子10,能提出多少次,就有几个0. 例如5!=120. 此时进行因式分解为: 10 ∗ ( 12 ) . 10*(12). 10∗(12).一共提出1个10,因此一共一个0.
- 10是由2和5构成的。而且5的个数绝对更少。例如120 = 5 ∗ ( 24 ) 5*(24) 5∗(24) = 2 ∗ 2 ∗ 2 ∗ ( 15 ) 2*2*2*(15) 2∗2∗2∗(15).我们发现5的个数决定了阶乘结果中可以和2组成几个10.
- 因此我们可以先尝试统计n的阶乘中,5的个数。试一下效果
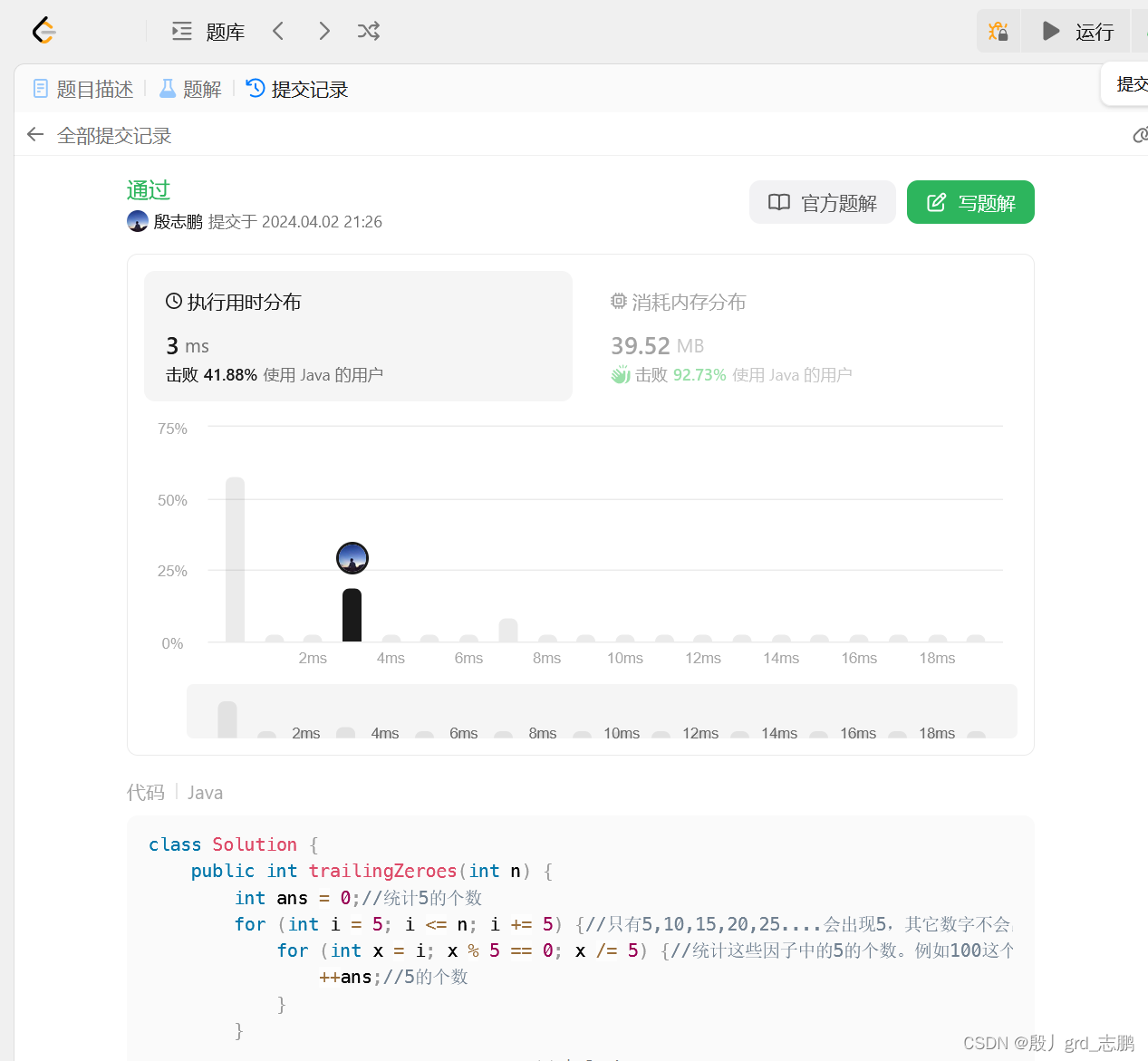
我们不需要每个阶乘数字都统计,例如5!中只有5这个数会出现5.因为5!=1*2*3*4*5.明眼人都知道,1,2,3,4不会有5的出现。
| 代码:最起码通过了对吗,说明想法没错,接下来法二会继续优化 |
|---|
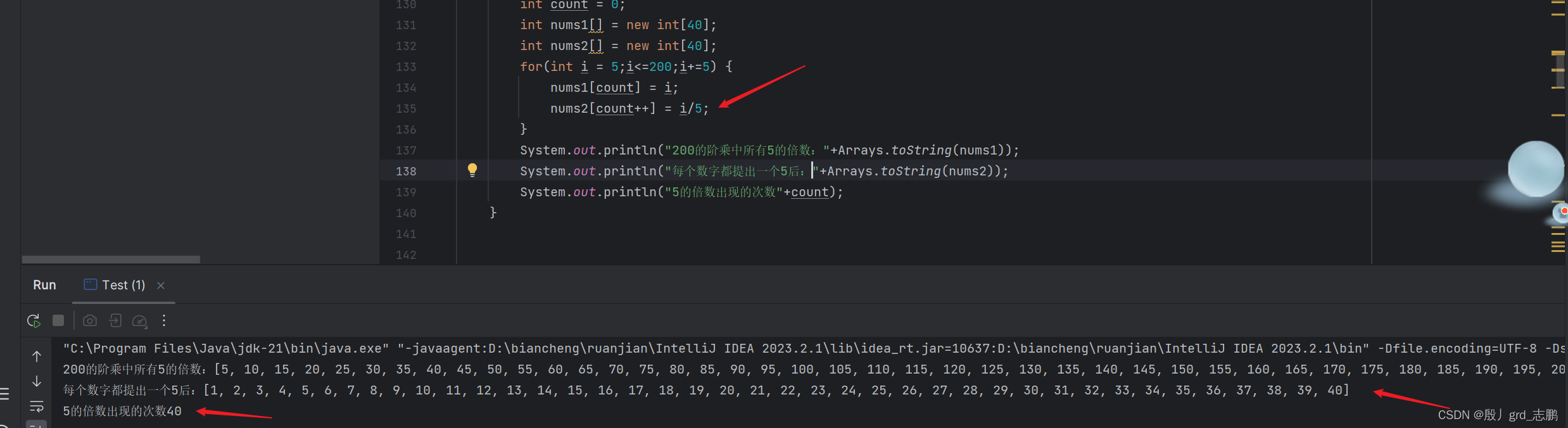
class Solution {public int trailingZeroes(int n) {int ans = 0;//统计5的个数for (int i = 5; i <= n; i += 5) {//只有5,10,15,20,25....会出现5,其它数字不会出现5for (int x = i; x % 5 == 0; x /= 5) {//统计这些因子中的5的个数。例如100这个因子,可以拆解为5*5*4.有两个5++ans;//5的个数}}return ans;}
}
数学优化:思路转变为求5的倍数的个数
| 解题思路:时间复杂度O( l o g 2 n log_2n log2n),空间复杂度O( 1 1 1) |
|---|
- 以1000为例:1000 = 5 ∗ 200 5*200 5∗200 = 5 ∗ 5 ∗ 40 5*5*40 5∗5∗40 = 5 ∗ 5 ∗ 5 ∗ 8 5*5*5*8 5∗5∗5∗8 = 5 ∗ 5 ∗ 5 ∗ 5 ∗ 8 5 5*5*5*5*\dfrac{8}{5} 5∗5∗5∗5∗58.则1000的阶乘的5的个数为200+40+8+1 = 249个
- 为什么对单个数字1000不断除5,可以求出1000的阶乘中5的个数呢?
- 因为我们需要转变思路,从现在开始,我们要统计从1到1000中,5的倍数出现的次数。
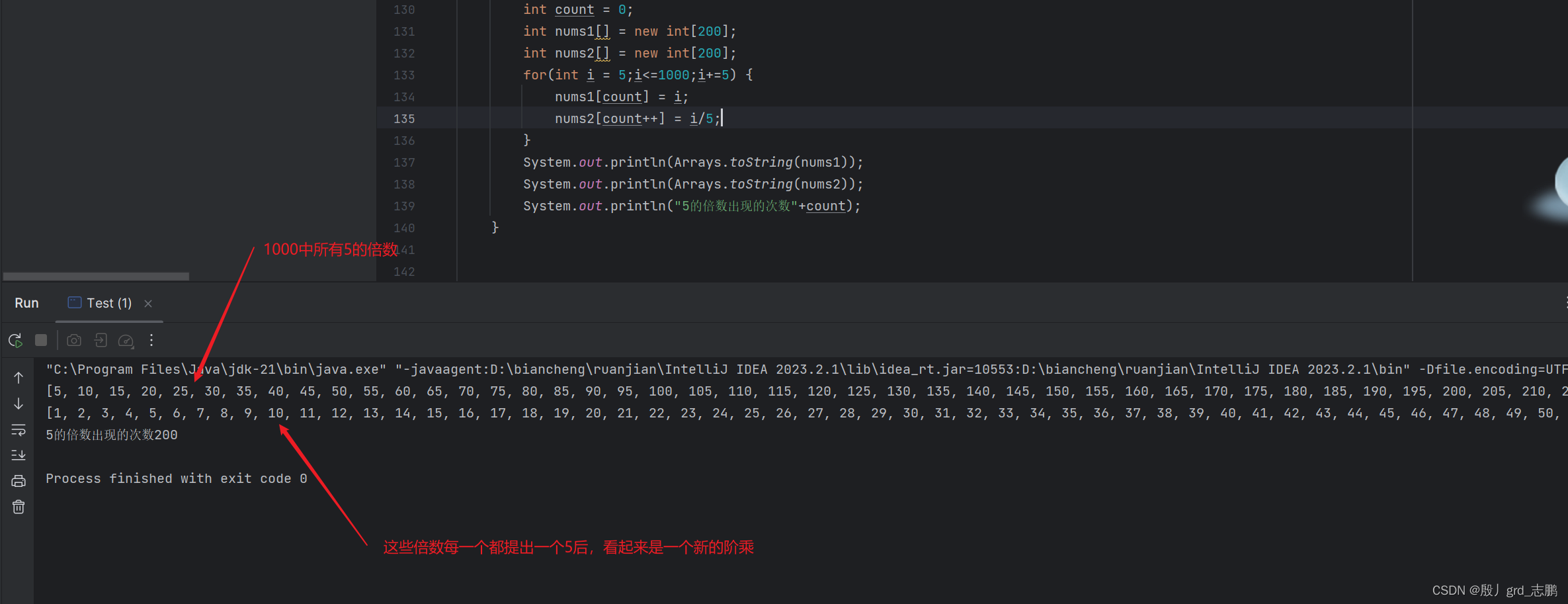
- 1到1000中,5的倍数出现200次, 200个5的倍数分别是 5 , 10 , 15 , 20 , . . . . . , 1000 5,10,15,20,.....,1000 5,10,15,20,.....,1000
- 此时如果我们将这200个5的倍数,全部提出一个5,就会获得200个5. 并且因式分解后剩下的值看起来如下: 1 ∗ 2 ∗ 3 ∗ 4 ∗ 5 ∗ . . . . ∗ 200 1*2*3*4*5*....*200 1∗2∗3∗4∗5∗....∗200,你会发现它们这些数正好组成了200的阶乘所有的数,
- 此时,我们只需要从1到200这些数中,找当中5的倍数的个数。也就是 5 , 10 , 15 , 20 , . . . , 200 5,10,15,20,...,200 5,10,15,20,...,200
- 而200这个阶乘中,5的倍数共出现40次,我们将40次进行统计,然后继续对这40个5的倍数提出一个5的因子。你会发现它们又变成了40的阶乘。
- 此时继续求40这个阶乘中,5的倍数出现的次数。结果如下:共8个5的倍数,我们将8个5提出后,剩下的数字组成了8的阶乘
- 继续对8求:共1个5的倍数5,提出1个5后,剩下数字只有1了,也就不用继续遍历了
- 最终,就可以将所有我们提出的5统计起来,200+40+8+1 = 249个。
| 代码 |
|---|
class Solution {public int trailingZeroes(int n) {int count = 0;//统计个数while (n != 0){//只要n的阶乘中还可以有5就继续n /= 5;//获取n这个阶乘中所有5的倍数的个数count += n;//统计个数}return count;}
}
相关文章:

java数据结构与算法刷题-----LeetCode172. 阶乘后的零
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 数学:阶乘的10因子个数数学优化:思路转变为求5的倍数…...
掌握数据相关性新利器:基于R、Python的Copula变量相关性分析及AI大模型应用探索
在工程、水文和金融等各学科的研究中,总是会遇到很多变量,研究这些相互纠缠的变量间的相关关系是各学科的研究的重点。虽然皮尔逊相关、秩相关等相关系数提供了变量间相关关系的粗略结果,但这些系数都存在着无法克服的困难。例如,…...
Centos7环境下安装MySQL8详细教程
1、下载mysql安装包 下载哪个版本,首先需要确定一下系统的glibc版本,使用如下命令: rpm -qa | grep glibc 2、检查是否安装过mysql ps:因为以前用yum安装过,所以先用yum卸载。如果不是此方式或者没安装过则跳过…...

趣学前端 | 综合一波CSS选择器的用法
背景 最近睡前习惯翻会书,重温了《HTML5与CSS 3权威指南》。这本书,分上下两册,之前读完了上册,下册基本没翻过。为了对得起花过的每一分钱,决定拾起来近期读一读。 CSS 选择器 在CSS3中,提倡使用选择器…...

数据库 06-04 恢复
01 一.事务故障 二.系统 三.磁盘 02. 重点是稳定存储器 组成...

基于MPPT的风力机发电系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1风能与风力发电机模型 4.2风力机功率特性与最大功率点 4.3 MPPT 5.完整工程文件 1.课题概述 基于MPPT的风力机发电系统simulink建模与仿真。MPPT使用S函数编写实现。基于最大功率点跟踪(…...

GD32F30x IO 复用问题
1.PE9 复用PWM 引脚 需要使能 gpio_pin_remap_config(GPIO_TIMER0_FULL_REMAP,ENABLE);...
BPMNJS 在原生HTML中的引入与使用
BPMNJS 在HTML中的引入与使用 在网上看到的大多是基于vue使用BPMN的示例或者教程,竟然没有在HTML使用的示例,有也是很简单的介绍核心库的引入和使用,并没有涉及到扩展库。于是简单看了下,真的是一波三折,坎坎坷坷。不…...

HarmonyOS 应用开发之通过数据管理服务实现数据共享静默访问
场景介绍 典型跨应用访问数据的用户场景下,数据提供方会存在多次被拉起的情况。 为了降低数据提供方拉起次数,提高访问速度,OpenHarmony提供了一种不拉起数据提供方直接访问数据库的方式,即静默数据访问。 静默数据访问通过数据…...

ubuntu强密码支持
接到新需求,欧盟需要ubuntu使用强密码,网络上找到一个包可以增加ubuntu密码增强机制,以下是调试过程。 sudo apt-get install libpam-pwquality 然后,编辑位于/etc/pam.d/目录中的common-password文件: sudo vim /et…...

C语言中文分词 Friso的使用教程
Friso是使用C语言开发的一款高性能中文分词器,使用流行的mmseg算法实现。完全基于模块化设计和实现,可以很方便的植入到其他程序中,例如:MySQL,PHP等。同时支持对UTF-8/GBK编码的切分。 官方地址:https://…...

MySQL中drop、truncate和delete的区别
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:每天一个知识点 ✨特色专栏:…...
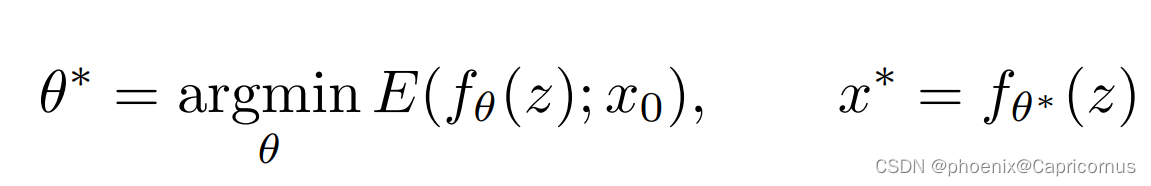
Deep Image Prior
自监督的开创性工作 从简单分布到复杂分布的映射,本质上是将重建限制到某一流形,在流形上通过观测图像的数据保真项作为监督。 称之为先验也是很准确,流形就是先验。 这个扰动也很关键,本质上一个平滑正则项。直观理解是各种扰动…...

leetcode148. 排序链表
方法1:插入方法进行改进 class Solution {public ListNode sortList(ListNode head) {/*想法:设置两个指针first,last分别指向当前有序子链表的头和尾节点;并遍历链表,当遍历到的节点值大于last的值时,就将该节点插入到有序子链表…...
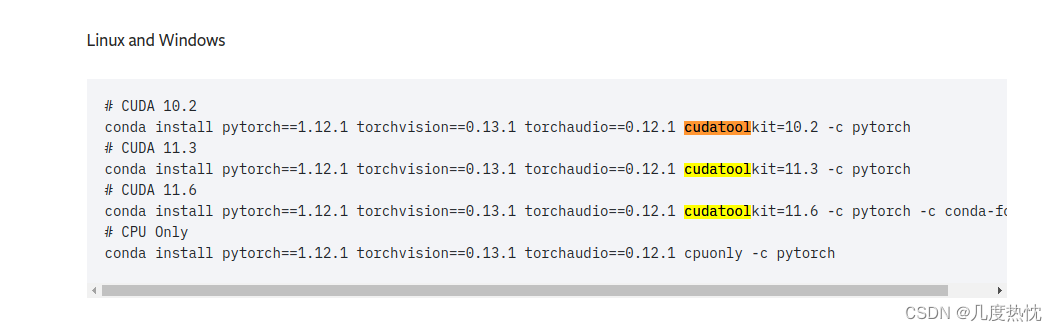
【深度学习环境配置】一文弄懂cuda,cudnn,NVIDIA Driver version,cudatoolkit的关系
【深度学习环境配置】一文弄懂cuda,cuDNN,NVIDIA Driver version,cudatoolkit的关系 NVIDIA Driver version(NVIDIA驱动程序)CUDAcuDNNcudatoolkit深度学习环境配置顺序 今天突然发现配置的环境有些问题,意…...

C语言中的字符与字符串:魔法般的函数探险
前言 在C语言的世界里,字符和字符串是两个不可或缺的元素,它们像是魔法般的存在,让文字与代码交织出无限可能。而在这个世界里,有一批特殊的函数,它们如同探险家,引领我们深入字符与字符串的秘境࿰…...
【JAVASE】带你了解面向对象三大特性之一(继承)
✅作者简介:大家好,我是橘橙黄又青,一个想要与大家共同进步的男人😉😉 🍎个人主页:再无B~U~G-CSDN博客 1.继承 1.1 为什么需要继承 Java 中使用类对现实世界中实体来…...
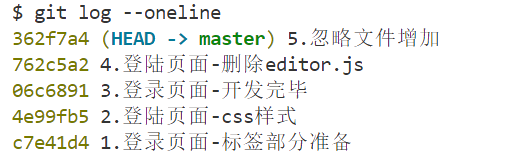
Git 如何去使用
目录 1. Git暂存区的使用 1.1. 暂存区的作用 1.2. 暂存区覆盖工作区(注意:完全确认覆盖时使用) 1.3. 暂存区移除文件 1.4. 练习 2. Git回退版本 2.1. 概念 2.2. 查看提交历史 2.3. 回退命令 2.4. 注意 3. Git删除文件 3.1. 需求 …...

C语言 | Leetcode C语言题解之第12题整数转罗马数字
题目: 题解: const char* thousands[] {"", "M", "MM", "MMM"}; const char* hundreds[] {"", "C", "CC", "CCC", "CD", "D", "DC"…...

【软件工程】测试规格
1. 引言 1.1简介 本次的测试用例是基于核心代码基本开发完毕,在第一代系统基本正常运行后编写的,主要目的是为了后续开发与维护的便利性。 该文档主要受众为该系统后续开发人员,并且在阅读此文档前最后先阅读本系统的需求文档、概要设计文…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...