蓝桥杯刷题 前缀和与差分-[2128]重新排序(C++)
问题描述
给定一个数组 A 和一些查询 L**i, R**i,求数组中第 L**i 至第 R**i 个元素之和。 小蓝觉得这个问题很无聊,于是他想重新排列一下数组,使得最终每个查询结果的和尽可能地大。小蓝想知道相比原数组,所有查询结果的总和最多可以增加多少?
输入格式
输入第一行包含一个整数 n。
第二行包含 n 个整数 A1, A2, · · · , A**n,相邻两个整数之间用一个空格分隔。
第三行包含一个整数 m 表示查询的数目。
接下来 m 行,每行包含两个整数 L**i、R**i ,相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
5
1 2 3 4 5
2
1 3
2 5样例输出
4样例说明
原来的和为 6 + 14 = 20,重新排列为 (1, 4, 5, 2, 3) 后和为 10 + 14 = 24,增
加了 4。
评测用例规模与约定
对于 30% 的评测用例,n, m ≤ 50 ;
对于 50% 的评测用例,n, m ≤ 500 ;
对于 70% 的评测用例,n, m ≤ 5000 ;
对于所有评测用例,1 ≤ n, m ≤ 10^5,1 ≤ A**i ≤ 10^6,1 ≤ L**i ≤ R**i ≤ 10^6 。
知识点:前缀和与差分
代码
通过90%测试样例代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
ll a[N],b[N],cnt[N];
ll sum1,sum2;
int main() {ll n,m,l,r;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=b[i-1]+a[i];}cin>>m;for(int i=1;i<=m;i++){cin>>l>>r;sum1+=b[r]-b[l-1];for(int j=l;j<=r;j++){cnt[j]++;}}sort(a+1,a+n+1);sort(cnt+1,cnt+n+1);for(int i=1;i<=n;i++){sum2+=a[i]*cnt[i];}cout<<sum2-sum1<<endl;return 0;
}通过100%测试样例代码(差分优化)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
ll a[N],b[N],cnt[N];
ll sum1,sum2;
void insert(ll l,ll r,ll c)
{cnt[l]+=c;cnt[r+1]-=c;
}
int main() {ll n,m,l,r;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=b[i-1]+a[i];}cin>>m;for(int i=1;i<=m;i++){cin>>l>>r;sum1+=b[r]-b[l-1];insert(l,r,1);}for(int i=1;i<=n;i++){cnt[i]+=cnt[i-1];}sort(a+1,a+n+1);sort(cnt+1,cnt+n+1);for(int i=1;i<=n;i++){sum2+=a[i]*cnt[i];}cout<<sum2-sum1<<endl;return 0;
}相关文章:
)
蓝桥杯刷题 前缀和与差分-[2128]重新排序(C++)
问题描述 给定一个数组 A 和一些查询 L**i, R**i,求数组中第 L**i 至第 R**i 个元素之和。 小蓝觉得这个问题很无聊,于是他想重新排列一下数组,使得最终每个查询结果的和尽可能地大。小蓝想知道相比原数组,所有查询结果的总和最多…...
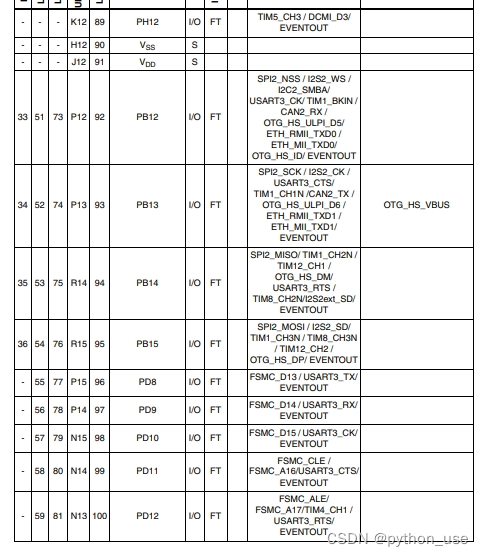
STM32重要参考资料
stm32f103c8t6 一、引脚定义图 二、时钟树 三、系统结构图 四、启动配置 (有时候不小心短接VCC和GND,芯片会锁住,可以BOOT0拉高试试(用跳线帽接)) 五、最小系统原理图 可用于PCB设计 六、常见折腾人bug…...
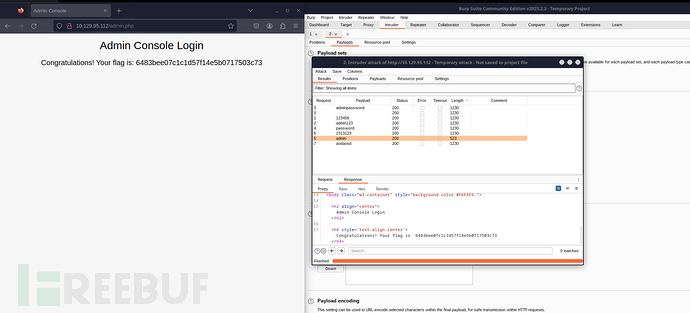
[StartingPoint][Tier0]Preignition
Task 1 Directory Brute-forcing is a technique used to check a lot of paths on a web server to find hidden pages. Which is another name for this? (i) Local File Inclusion, (ii) dir busting, (iii) hash cracking. (目录暴力破解是一种用于检查 Web 服务器上的大…...
第三节 关系数据库标准语言SQL(Ⅴ))
数据库系统概论(超详解!!!)第三节 关系数据库标准语言SQL(Ⅴ)
1.数据更新 1.插入数据 1.插入元组 语句格式 INSERT INTO <表名> [(<属性列1>[,<属性列2 >…)] VALUES (<常量1> [,<常量2>]… ); 功能:将新元组插入指定表中 INTO子句 : 指定要插入数据的表名及…...

SpringBoot | Spring Boot“整合Redis“
目录: 1. Redis 介绍2. Redis 下载安装3. Redis “服务开启”和“连接配置”4. Spring Boot整合Redis的“前期准备” :① 编写实体类② 编写Repository 接口③ 在“全局配置文件”中添加 “Redis数据库” 的 “相关配置信息” 5. Spring Boot整合“Redis” (案例展示) 作者简介…...
)
SV学习笔记(四)
OCP Open Closed Principle 开闭原则 文章目录 随机约束和分布为什么需要随机?为什么需要约束?我们需要随机什么?声明随机变量的类什么是约束权重分布集合成员和inside条件约束双向约束 约束块控制打开或关闭约束内嵌约束 随机函数pre_random…...

Midjourney艺术家分享|By Moebius
Moebius,本名让吉拉德(Jean Giraud),是一位极具影响力的法国漫画家和插画师,以其独特的科幻和幻想风格而闻名于世。他的艺术作品不仅在漫画领域内受到高度评价,也为电影、时尚和广告等多个领域提供了灵感。…...

Vue - 1( 13000 字 Vue 入门级教程)
一:Vue 导语 1.1 什么是 Vue Vue.js(通常称为Vue)是一款流行的开源JavaScript框架,用于构建用户界面。Vue由尤雨溪在2014年开发,是一个轻量级、灵活的框架,被广泛应用于构建单页面应用(SPA&am…...

Vue关键知识点
watch侦听器 Vue.js 中的侦听器(Watcher)是 Vue提供的一种响应式系统的核心机制之一。 监听数据的变化,并在数据发生变化时执行相应的回调函数。 目的:数据变化能够自动更新到视图中 原理: Vue 的侦听器通过观察对象的属性&#…...

Prometheus+grafana环境搭建redis(docker+二进制两种方式安装)(四)
由于所有组件写一篇幅过长,所以每个组件分一篇方便查看,前三篇 Prometheusgrafana环境搭建方法及流程两种方式(docker和源码包)(一)-CSDN博客 Prometheusgrafana环境搭建rabbitmq(docker二进制两种方式安装)(二)-CSDN博客 Prometheusgrafana环境搭建m…...
)
宝塔面板安装nginx流媒体服务器(http-flv)
前文介绍了使用nginx搭建流媒体服务器,实现了hls切片方式播放,不过延迟较长。本文采用nginx搭建支持http-flv方式的流媒体服务器,用以测试期性能。 目录 一、服务器操作系统安装 二、在控制台安装宝塔面板...
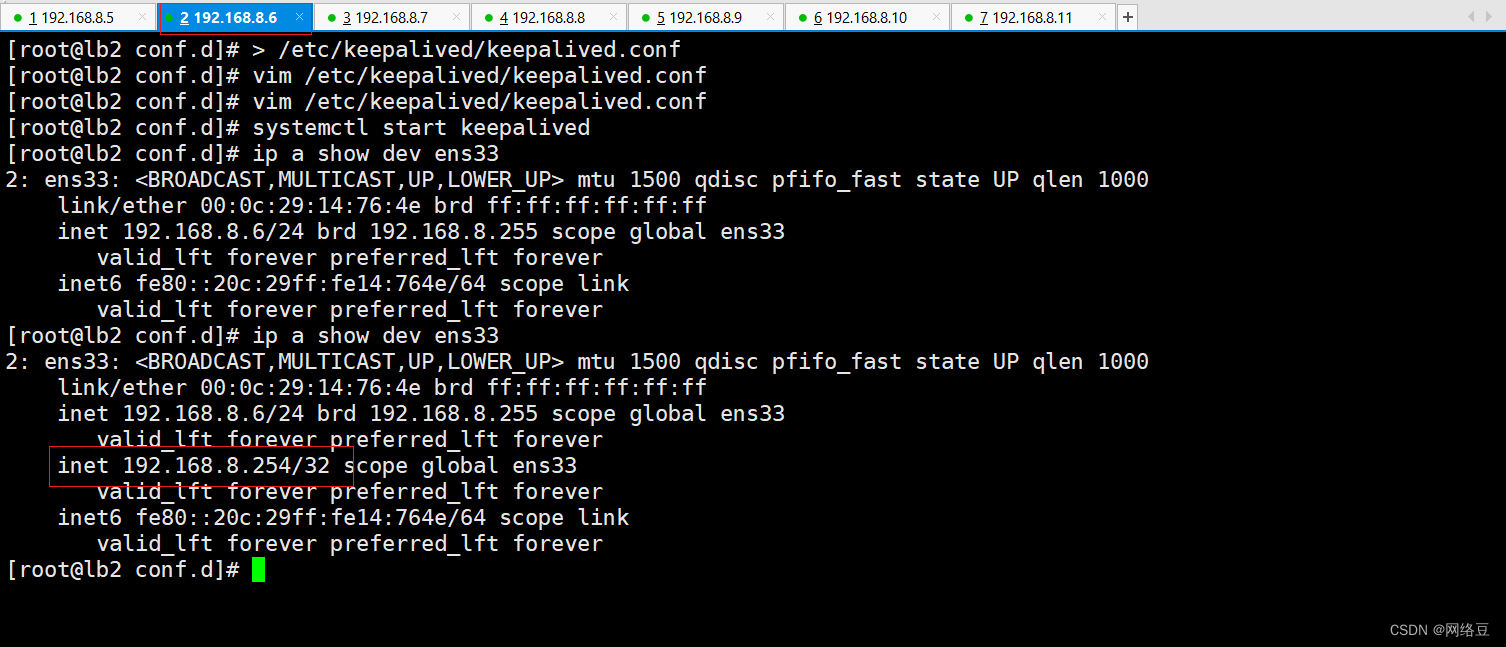
LNMP环境:揭秘负载均衡与高可用性设计
lb1: 192.168.8.5 lb2: 192.168.8.6 web1:192.168.8.7 web2:192.168.8.8 php-fpm: 192.168.8.9 mysql: 192.168.8.10 nfs:192.168.8.11 分别插入镜像 8.5-8.8 分别安装nginx,并设置启动 8.9 安装php 8.10 安装mysql 先配置一台web服务器然后同步 设置网站根目录 cp -…...
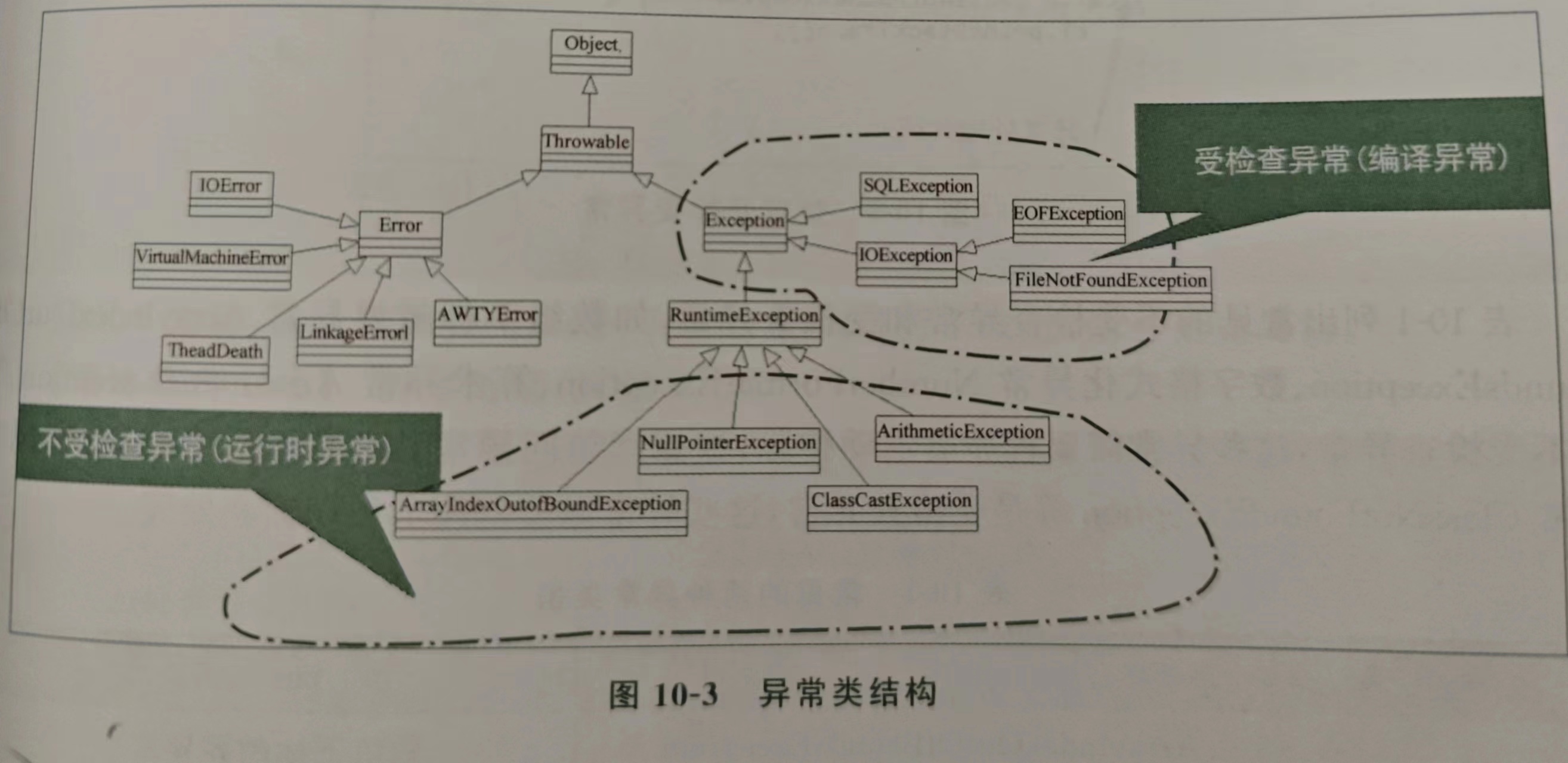
深入理解Java异常处理机制(day20)
异常处理 异常处理是程序运行过程产生的异常情况进行恰当的处理技术 在计算机编程里面,异常的情况比所我们所想的异常情况还要多。 Java里面有两种异常处理方式; 1.利用trycatchfinaly语句处理异常,优点是分开了处理异常代码和程序正常代码…...
Docker实战教程 第1章 Linux快速入门
2-1 Linux介绍 为什么要学Linux 三个不得不学习 课程需要:Docker开发最好在Linux环境下。 开发需要:作为一个后端程序员,是必须要掌握Linux的,这是找工作的基础门槛。 运维需要:在服务器端,主流的大型服…...

java数据结构与算法刷题-----LeetCode172. 阶乘后的零
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 数学:阶乘的10因子个数数学优化:思路转变为求5的倍数…...
掌握数据相关性新利器:基于R、Python的Copula变量相关性分析及AI大模型应用探索
在工程、水文和金融等各学科的研究中,总是会遇到很多变量,研究这些相互纠缠的变量间的相关关系是各学科的研究的重点。虽然皮尔逊相关、秩相关等相关系数提供了变量间相关关系的粗略结果,但这些系数都存在着无法克服的困难。例如,…...
Centos7环境下安装MySQL8详细教程
1、下载mysql安装包 下载哪个版本,首先需要确定一下系统的glibc版本,使用如下命令: rpm -qa | grep glibc 2、检查是否安装过mysql ps:因为以前用yum安装过,所以先用yum卸载。如果不是此方式或者没安装过则跳过…...

趣学前端 | 综合一波CSS选择器的用法
背景 最近睡前习惯翻会书,重温了《HTML5与CSS 3权威指南》。这本书,分上下两册,之前读完了上册,下册基本没翻过。为了对得起花过的每一分钱,决定拾起来近期读一读。 CSS 选择器 在CSS3中,提倡使用选择器…...

数据库 06-04 恢复
01 一.事务故障 二.系统 三.磁盘 02. 重点是稳定存储器 组成...

基于MPPT的风力机发电系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1风能与风力发电机模型 4.2风力机功率特性与最大功率点 4.3 MPPT 5.完整工程文件 1.课题概述 基于MPPT的风力机发电系统simulink建模与仿真。MPPT使用S函数编写实现。基于最大功率点跟踪(…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
