PCA(Principal Component Analysis,主成分分析)
PCA(Principal Component Analysis,主成分分析)是一种在数据分析中广泛应用的统计方法,主要用于数据降维、可视化和去噪。以下是对PCA的发展史、工作原理以及理论基础的详细解释:
Principal Component Analysis
- 一、PCA的发展史
- 二、PCA的工作原理
- 三、PCA的理论基础
- 总结
一、PCA的发展史
PCA方法的历史可以追溯到较早的统计学和数学领域。然而,其作为主成分分析的概念和术语的明确提出,则是在20世纪初。随着计算机技术的发展,PCA在数据处理和分析中的应用越来越广泛。特别是在现代数据分析中,PCA已经成为一种标准的工具,用于从高维数据中提取关键信息,降低数据的复杂性,同时保留其最重要的特征。
二、PCA的工作原理
PCA的工作原理的核心目标是将原始的高维数据映射到一个低维空间,同时尽可能保留数据中的关键信息。具体步骤如下:
- 计算协方差矩阵:首先,PCA会计算数据集中各变量之间的协方差矩阵。这个矩阵包含了变量之间的线性相关性信息。
- 特征值分解:接着,PCA会对协方差矩阵进行特征值分解。这个过程会找到协方差矩阵的特征向量和特征值。特征向量代表了数据的主要变化方向,而特征值则衡量了这些方向上数据变化的程度。
- 选择主成分:根据特征值的大小,PCA会选择前几个最大的特征值对应的特征向量作为主成分。这些主成分代表了数据中的主要变化模式,且彼此之间是正交的(即不相关)。
- 数据转换:最后,PCA会将原始数据转换到由这些主成分构成的新坐标系中。这个过程相当于将数据投影到低维空间,实现了数据的降维。
三、PCA的理论基础
PCA的理论基础主要建立在线性代数和统计学之上。以下是几个关键概念:
- 基变换:PCA通过基变换将原始数据从高维空间映射到低维空间。这种变换是通过选择新的基向量(即主成分)来实现的,这些基向量能够最好地表示原始数据的主要特征。
- 协方差和散度矩阵:协方差矩阵衡量了变量之间的线性相关性,而散度矩阵则描述了数据的分布情况。PCA通过计算这些矩阵来找到数据的主要变化方向和程度。
- 特征值分解和SVD分解:这两种数学工具都是PCA实现数据降维的关键。特征值分解用于找到协方差矩阵的特征向量和特征值,而SVD(奇异值分解)则是一种更一般的矩阵分解方法,也可以用于PCA的计算。
- 信息保留:PCA的目标是在降维的同时尽可能保留原始数据中的信息。这通过选择最大的特征值对应的特征向量作为主成分来实现,因为这些方向上的数据变化最大,包含了最多的信息。
总结
总的来说,PCA是一种强大的数据分析工具,它通过降维技术将高维数据转化为低维表示,同时保留数据的主要特征。其工作原理基于线性代数和统计学的理论基础,通过计算协方差矩阵、特征值分解等步骤实现数据的降维和信息的提取。
相关文章:

PCA(Principal Component Analysis,主成分分析)
PCA(Principal Component Analysis,主成分分析)是一种在数据分析中广泛应用的统计方法,主要用于数据降维、可视化和去噪。以下是对PCA的发展史、工作原理以及理论基础的详细解释: Principal Component Analysis 一、PC…...
干货 | 探索CUTTag:从样本到文库,实验步步为营!
CUT&Tag(Cleavage Under Targets and Tagmentation)是一种新型DNA-蛋白互作研究技术,主要用于研究转录因子或组蛋白修饰在全基因组上的结合或分布位点。相比于传统的ChIP-seq技术,CUT&Tag反应在细胞内进行,创新…...

提质不增本,降本不降质
#公益巡讲# #质量万里行# 公开课、沙龙活动...

数据结构---顺序表实现
目录 1.顺序表 2.动态顺序表的实现 (4)顺序表初始化 (5)顺序表销毁 (6)顺序表的插入 a.尾插 b.头插 (7)顺序表的删除 a.尾删 b.头删 (8)指定位置之…...

python docx 添加动态表格
在Python中,使用python-docx库可以创建Word文档并添加动态表格。以下是一个简单的例子,演示如何创建一个包含动态内容的表格: from docx import Document# 创建一个Word文档 document Document()# 添加一个标题 document.add_heading(动态表…...
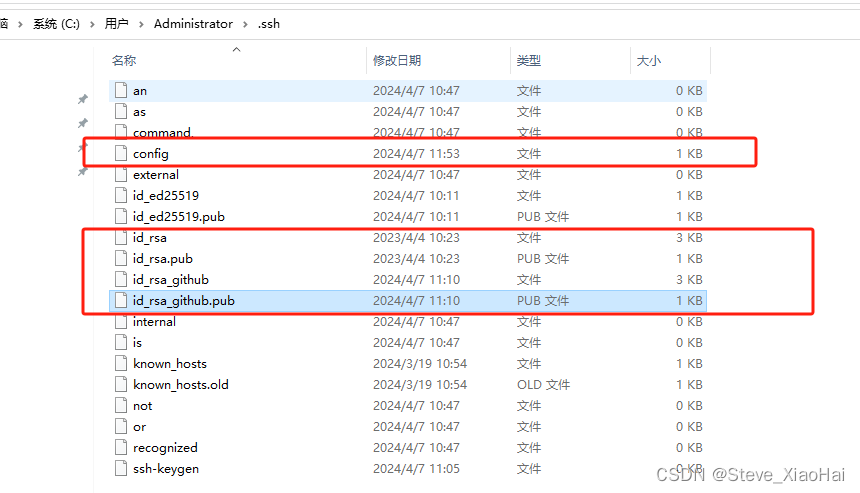
git配置多SSH
目的: 一台电脑可以让github、gitee等账号同时存在,让不同账号配置不同的密钥 第一步:创建不同平台的SSH公钥 执行命令: ssh-keygen -t rsa -C "对应仓库邮箱地址" -f ~/.ssh/id_rsa.github 如果执行上面的命令&…...
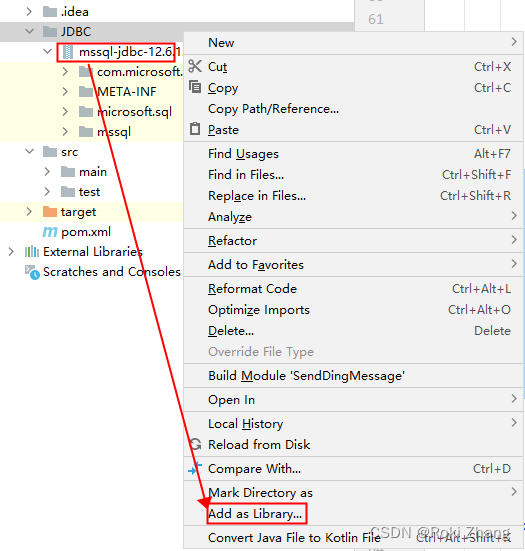
IDEA连接SqlServer数据库
目录 下载jar包 下载sqljdbc_12.6压缩包 解压 导入IDEA 新建文件夹 复制粘贴进JDBC文件夹并设为library 编写类及方法 代码 下载jar包 以sqljdbc_12.6为例 下载sqljdbc_12.6压缩包 最新地址:sqljdbc 官方最新地址 解压 解压即用 导入IDEA 新建文件夹 复制…...
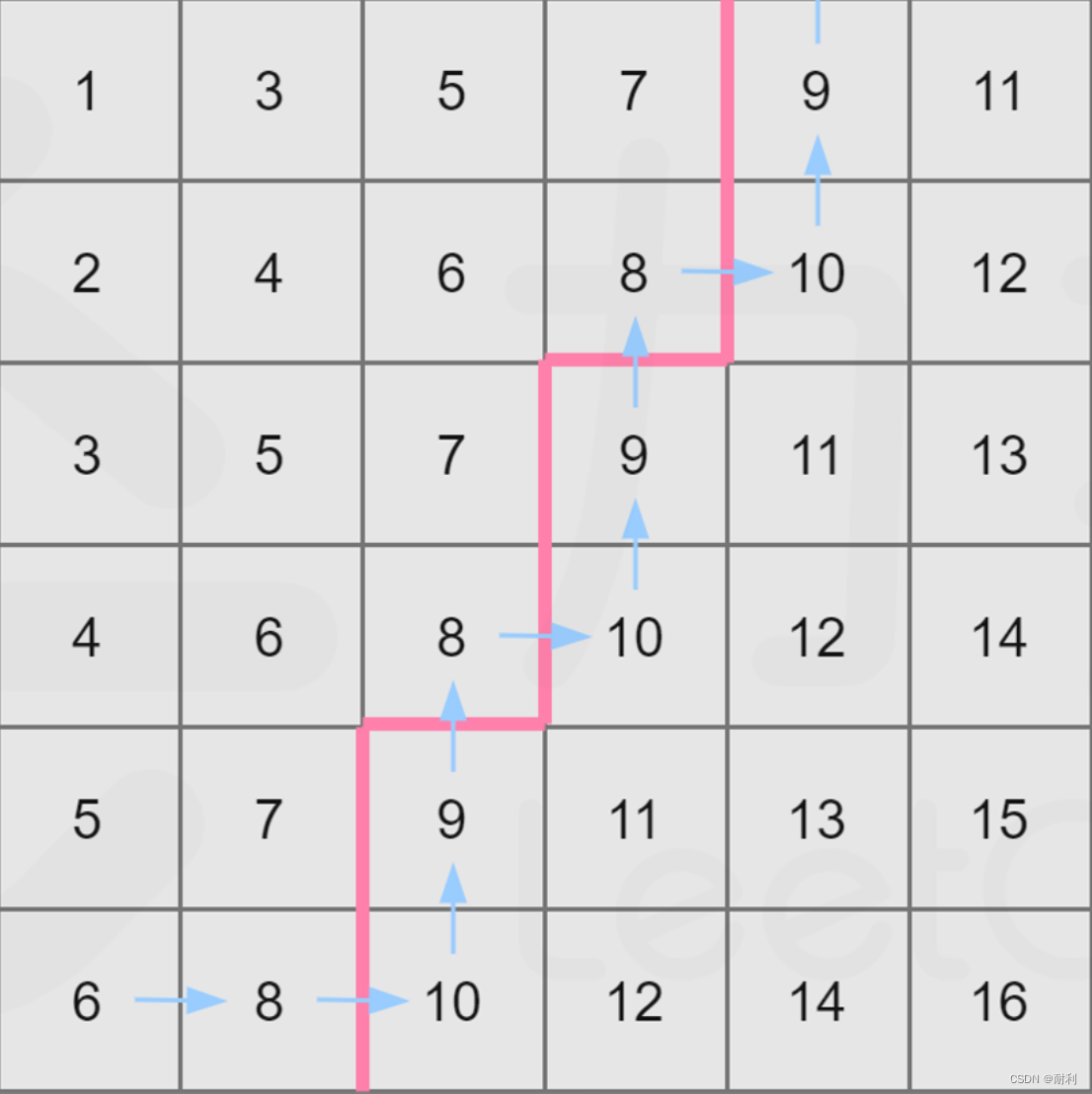
LeetCode 378 有序矩阵中第K小的元素
题目信息 LeetoCode地址: . - 力扣(LeetCode) 题解内容大量转载于:. - 力扣(LeetCode) 题目理解 题意很直观,就是求二维矩阵中所有元素排序后第k小的数。 最小堆写法 该写法不再赘述,维护…...

Vue3(domdiff)最长递归子序列求解简易版(超简单)
Vue3(domdiff)最长递归子序列求解简易版 ⚠️ 关键词(每一个都需要理解)js 代码实现写完感想欢迎关注 ⚠️ 关键词(每一个都需要理解) 动态规划(O(N^2))(不提倡…...

LLaMA-Factory+qwen多轮对话微调
LLaMA-Factory地址:https://github.com/hiyouga/LLaMA-Factory/blob/main/README_zh.md qwen地址:https://huggingface.co/Qwen/Qwen-7B-Chat/tree/main 数据准备 数据样例 [ {"id": "x3959", "conversations": [{&qu…...

邦芒面试:如何在面试中巧妙回答自己的缺点
在面试中,被问及自己的缺点时,如何巧妙回答是一门学问。恰当的回答不仅能够展示你的自我认知,还能让面试官看到你的成长潜力和积极态度。 首先,切忌谈一些看似缺点实则优点的话题,如追求完美、待人接物太客气等。这些…...

Android:身份证识别功能实现
说明: 此文使用华为SDK、百度SDK、百度在线API三种方式实现。 一、使用华为SDK实现身份证识别: 说明:免费,不需要联网。 1.AndroidManifest.xml添加权限:<uses-permission android:name"android.permissio…...

MacOS安装Homebrew教程
安装 Homebrew 是在 macOS 上管理软件包的一种简便方法。以下是安装 Homebrew 的步骤: 打开终端:你可以通过在 Spotlight 搜索栏中输入“终端”并按下回车键来打开 macOS 的终端应用程序。 执行安装命令:在终端中粘贴以下命令并按下回车键执…...

laravel如何通过DB获取一条数据并转成数组
在 Laravel 中,你可以使用原生数据库查询构建器(DB facade)来获取一条数据,并将其转换为数组。这可以通过在查询链的末尾调用 first() 方法后,使用 toArray() 方法来实现。first() 方法会返回一个 StdClass 对象&#…...
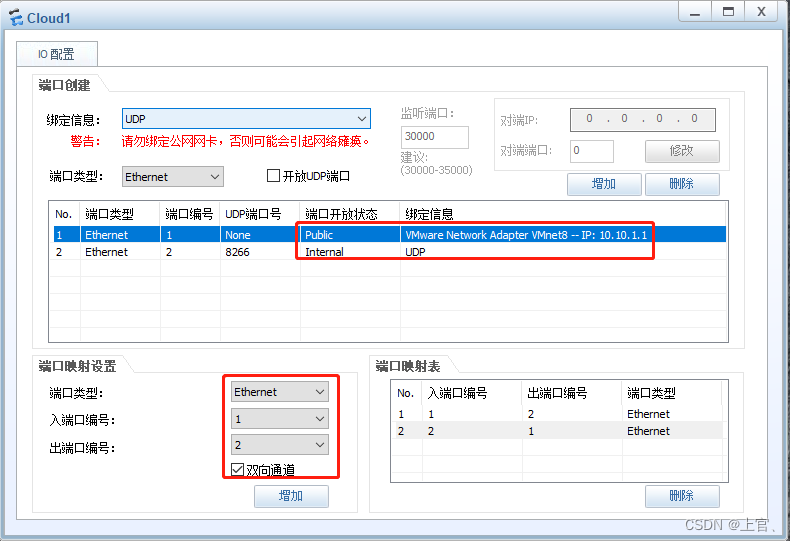
ENSP USG防火墙接入虚拟机;开启Web访问;
1.添加防火墙及云,启动防火墙; 2.配置桥接网卡; 默认账户:admin 默认密码:Admin123 #第一次登陆需修改密码; 默认G0/0/0口为管理口,而在模拟器中进入防火墙的web需如下配置: 配置 …...
数据结构算法题(力扣)——链表
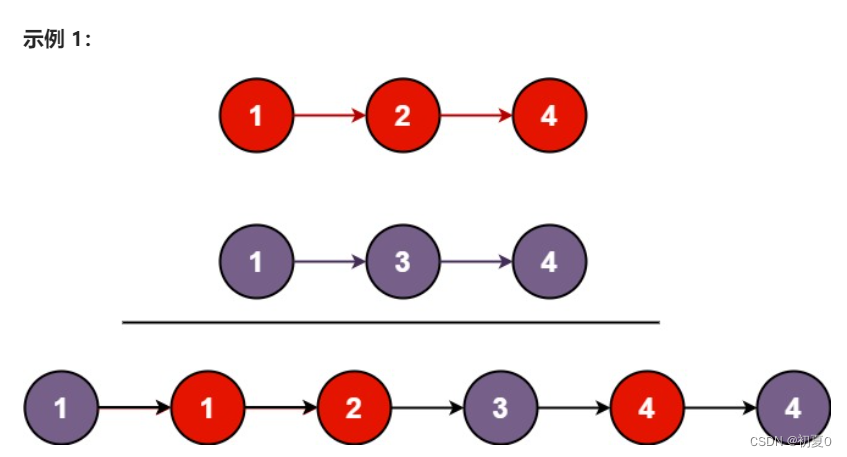
以下题目建议大家先自己动手练习,再看题解代码。这里只提供一种做法,可能不是最优解。 1. 移除链表元素(OJ链接) 题目描述:给一个链表的头节点 head 和一个整数 val ,删除链表中所有满足值等于 val 的节点…...

LeetCode---391周赛
题目列表 3099. 哈沙德数 3100. 换水问题 II 3101. 交替子数组计数 3102. 最小化曼哈顿距离 一、哈沙德数 简单的模拟题,代码如下 class Solution { public:int sumOfTheDigitsOfHarshadNumber(int x) {int s 0, tmp x;while(tmp){stmp%10;tmp/10;}return x…...

微信小程序的页面交互2
一、自定义属性 (1)定义: 微信小程序中的自定义属性实际上是由data-前缀加上一个自定义属性名组成。 (2)如何获取自定义属性的值? 用到target或currentTarget对象的dataset属性可以获取数据 ÿ…...
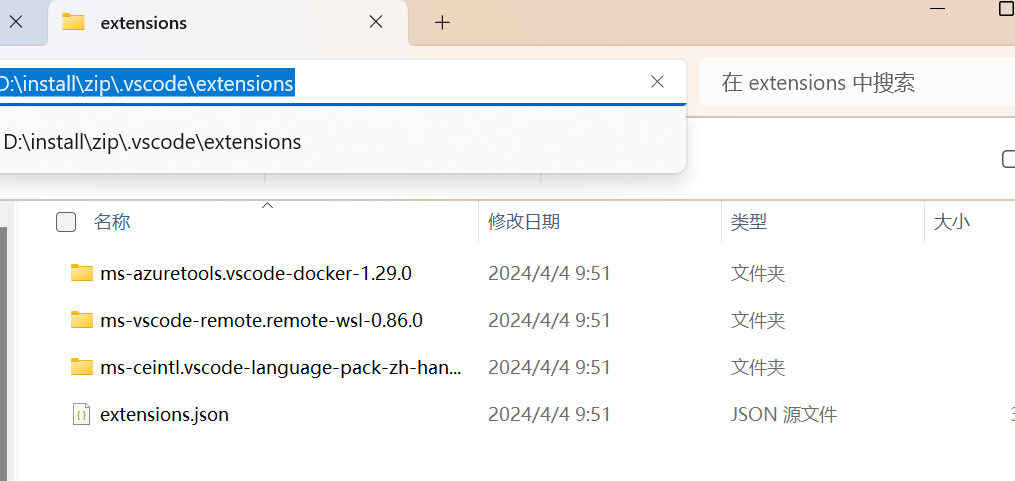
【VSCode】修改插件地址
不想放在原始C盘下面C:\Users\{用户}\.vscode\extensions为了后续存储空间考虑,想通过添加环境变量创建名为VSCODE_EXTENSIONS的环境变量,内容指向vs Code扩展所在目录即可 直接配置环境变量,不要在有空格的文件夹下面 变量名称:…...
自然语言处理NLP概述
大家好,自然语言处理(NLP)是计算机科学领域与人工智能领域中的一个重要方向,其研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。本文将从自然语言处理的本质、原理和应用三个方面,对其进行概述。 一、NLP的本质 NLP是一种…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
