算法第三十九天-验证二叉树的前序序列化
验证二叉树的前序序列化
题目要求


解题思路
方法一:栈
栈的思路是「自底向上」的想法。下面要结合本题是「前序遍历」这个重要特点。
我们知道「前序遍历」是按照「根节点-左子树-右子树」的顺序遍历的,只有当根节点的所有左子树遍历完成之后,才会遍历右子树。对于本题的输入,我们可以先判断「左子树」是否有效的,然后再判断「右子树」是否有效的,最后判断「根节点-左子树-右子树」是否为有效的。这个思路类似于递归,而把递归改写成循环时,就会使用「栈」,这就是本题使用「栈」的原因。
下面的重点是如何判断一棵子树是否有效?首先考虑最简单情况:怎么判断一个节点是叶子节点?很明显,当一个节点的两个孩子都是 "#"(空)的时候,该节点就是叶子节点。

当一个节点不是叶子节点的时候,那么它必定至少有一个孩子非空!有两种情况:
两个孩子都非"#"(空);
一个孩子为"#"(空),另一个孩子非"#"(空);
为了兼容这两个情况,我们想出了本题的一个重磅级的技巧:把有效的叶子节点使用 "#" 代替。 比如把 4## 替换成 # 。此时,叶子节点会变成空节点!
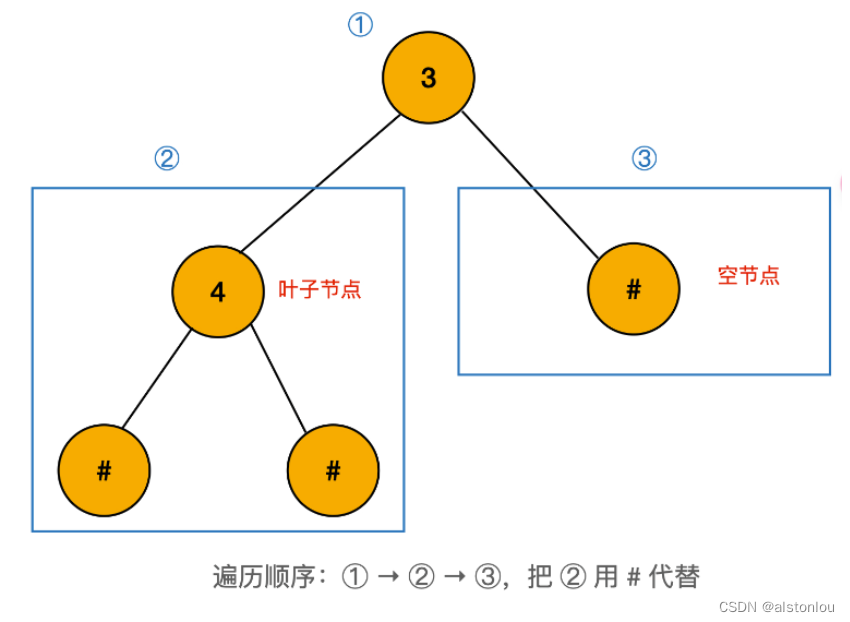
具体操作流程示例如下:
如输入:"9,3,4,#,#,1,#,#,2,#,6,#,#",当遇到 x,#,# 的时候,就把它变为 #。
模拟一遍过程:
[9,3,4,#,#] => [9,3,#],继续[9,3,#,1,#,#] => [9,3,#,#] => [9,#],继续[9,#2,#,6,#,#] => [9,#,2,#,#] => [9,#,#] => [#],结束
方法二:计算入度出度
背景知识:
- 入度:有多少个节点指向它;
- 出度:它指向多少个节点。
我们知道在树(甚至图)中,所有节点的入度之和等于出度之和。可以根据这个特点判断输入序列是否为有效的!
在一棵二叉树中:
- 每个空节点(
"#")会提供 0 个出度和 1 个入度。 - 每个非空节点会提供 2 个出度和 1 个入度(根节点的入度是 0)。
我们只要把字符串遍历一次,每个节点都累加 diff = 出度 - 入度 。在遍历到任何一个节点的时候,要求diff >= 0,原因是还没遍历到该节点的子节点,所以此时的出度应该大于等于入度。当所有节点遍历完成之后,整棵树的 diff == 0。
这里解释一下为什么下面的代码中 diff 的初始化为 1。因为,我们加入一个非空节点时,都会对 diff 先减去 1(入度),再加上 2(出度)。但是由于根节点没有父节点,所以其入度为 0,出度为 2。因此 diff 初始化为 1,是为了在加入根节点的时候,diff 先减去 1(入度),再加上 2(出度),此时 diff 正好应该是2.
代码
方法一:
class Solution(object): def isValidSerialization(self, preorder): stack = [] for node in preorder.split(','): stack.append(node) while len(stack) >= 3 and stack[-1] == stack[-2] == '#' and stack[-3] != '#': stack.pop(), stack.pop(), stack.pop() stack.append('#') return len(stack) == 1 and stack.pop() == '#'
方法二:
class Solution(object): def isValidSerialization(self, preorder): nodes = preorder.split(',') diff = 1 for node in nodes: diff -= 1 if diff < 0: return Falseif node != '#': diff += 2 return diff == 0
复杂度分析
方法一:
- 时间复杂度: O ( N ) O(N) O(N)
- 空间复杂度: O ( N ) O(N) O(N)
方法二:
- 时间复杂度: O ( N ) O(N) O(N)
- 空间复杂度: O ( 1 ) O(1) O(1)
参考
负雪明烛
相关文章:

算法第三十九天-验证二叉树的前序序列化
验证二叉树的前序序列化 题目要求 解题思路 方法一:栈 栈的思路是「自底向上」的想法。下面要结合本题是「前序遍历」这个重要特点。 我们知道「前序遍历」是按照「根节点-左子树-右子树」的顺序遍历的,只有当根节点的所有左子树遍历完成之后…...
)
Rust---复合数据类型之字符串与切片(2)
目录 字符串操作删除 (Delete)连接 (Concatenate)字符串转义前情回顾: Rust—复合数据类型之字符串(1) 字符串操作 删除 (Delete) 删除方法仅适用于 String 类型,分别是: pop(),remove(),truncate(),clear(),此外还有drain() 方法。 pop 方法:pop() 方法返回一个 O…...
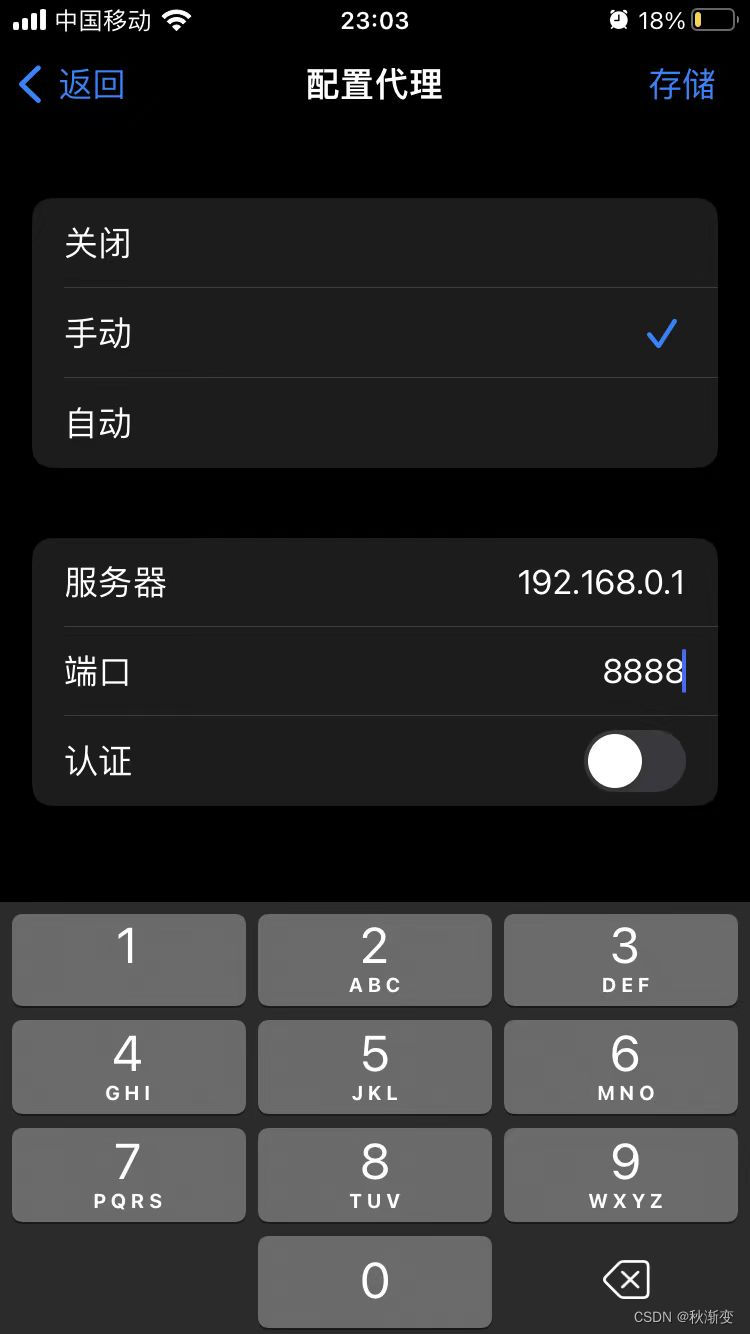
iOS 应用内网络请求设置代理
主要通过URLSessionConfiguration 的connectionProxyDictionary 属性 为了方便其他同学使用,我们可以通过界面来进行设定(是否开启代理、服务端、端口),从而达到类似系统上的设定 具体链接参考:为 iOS 网络请求设置代理…...

什么是MariaDB
2024年4月6日,周六晚上 今晚在Debian12上安装mysql时,运行后却发现是MariaDB MariaDB是一个开源的关系型数据库管理系统(RDBMS),它是MySQL的一个分支和替代品。MariaDB由MySQL的原始开发者之一Michael "Monty&qu…...
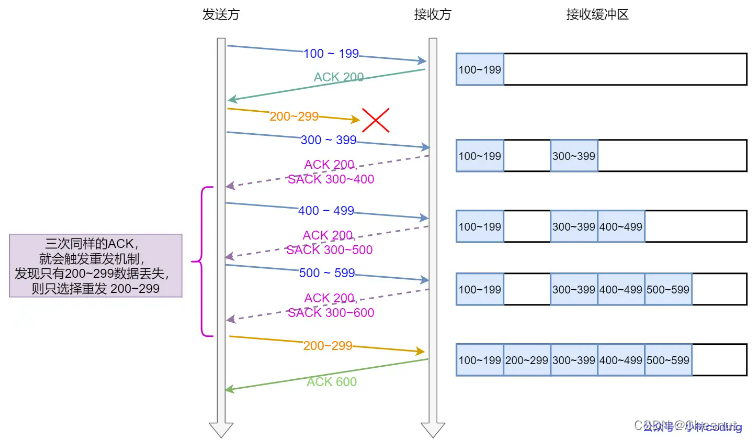
【面试八股总结】传输控制协议TCP(三)
参考资料 :小林Coding、阿秀、代码随想录 一、TCP拥塞控制⭐ 1. 慢启动 – Slow Start 慢启动是指TCP连接刚建立,一点一点地提速,试探一下网络的承受能力,以免直接扰乱了网络通道的秩序。 慢启动算法: 初始拥塞窗口…...

今年过去了多少天?(switch)
//今年已经过去了几天? #include <stdio.h> int monthday(int year,int month){switch(month){case 1:return 31;case 2:if ((year % 4 0 && year % 100 ! 0)||year % 400 0){return 29;}else{return 28;}break;case 3:return 31;case 4:return 30;…...
提升团队工程交付能力,从“看见”工程活动和研发模式开始
作者:张裕、雅纯 理想中的研发团队应当具有以下特征: 总是工作在最高优先级的事项上 理想的研发团队能够识别并始终集中精力在当前最紧迫和最有价值的任务上。这需要团队具备出色的项目管理能力和决策能力,以便能够正确评估优先级࿰…...

前端学习之DOM编程案例:全选反选案例
代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>全选反选</title> </head> <body><input type"checkbox" id"all">全选<ul><li><…...

golang map
1.底层实现 2.如何解决hash冲突 3.扩容机制 4.无序 5.非线程安全 6.不可寻址 runtime/map.go 1.底层实现 底层基于hash表实现,实现有2个结构体hmap,bmap,map由若干个桶存储,每个桶存8个元素,使用链地址解决hash冲突 …...

设计模式:享元模式案例
让我们以游戏开发中的棋类游戏(例如国际象棋)为例来展示享元模式的代码实现。在这个例子中,棋子的类型是内部状态,而棋子的位置是外部状态。 Java 代码示例 import java.util.HashMap; import java.util.Map;// 享元接口 interf…...
)
pandas(day5)
一. 检测重复值 1.1 检测 data pd.read_csv("./teacher/订单数据.csv")检测行与行之前是否有重复值 data.drop_duplicates()检测 列是否有重复值出现, keep first 从前往后判定 , last是从后往前判定data.drop_duplicates(subset["产…...
如何注册midjourney账号
注册Midjourney账号比较简单,准备好上网工具,进入官网 Midjourney访问地址: https://www.midjourney.com/ 目前没有免费使用额度了,会员最低 10 美元/月,一般建议使用30美元/月的订阅方案。了解如何订阅可以查看订阅…...
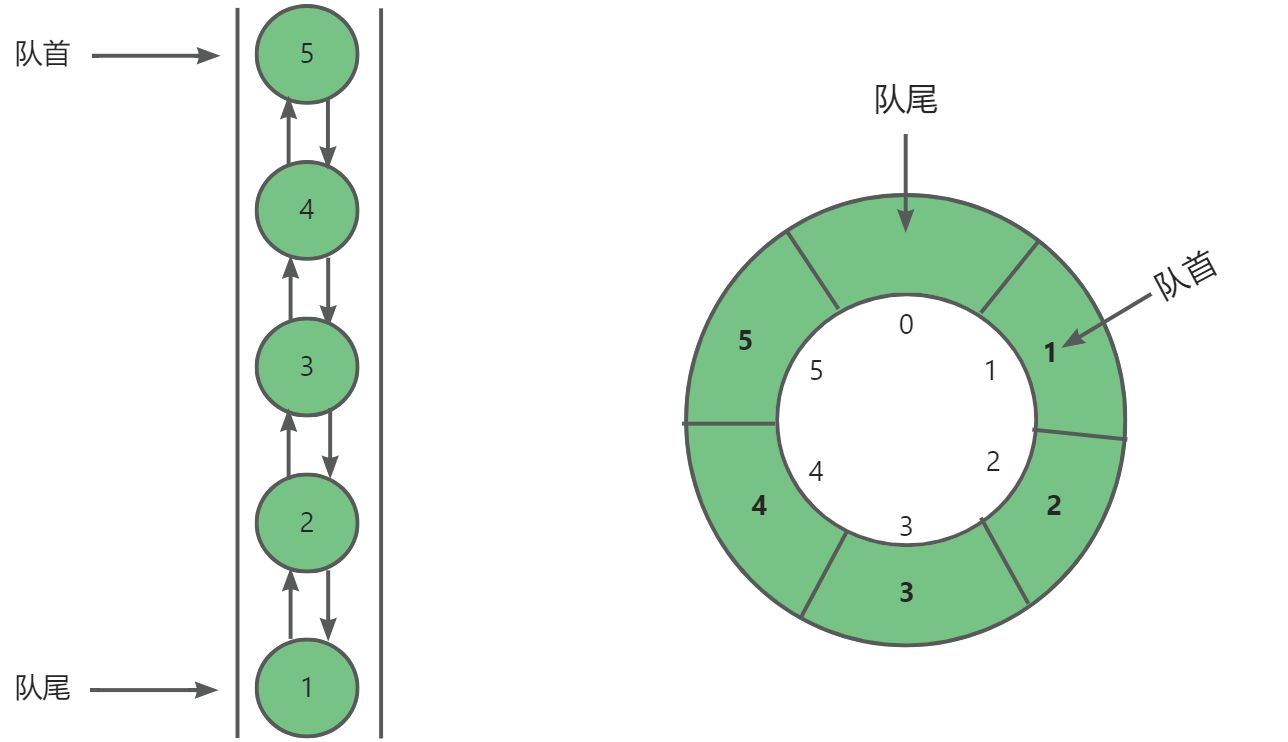
探索数据结构:特殊的双向队列
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 双向队列的定义 **双向队列(double‑ended queue)**是一种特殊的队列…...

16_I2C库函数
I2C库函数 1.void I2C_DeInit(I2C_TypeDef* I2Cx);2.void I2C_Init(I2C_TypeDef* I2Cx, I2C_InitTypeDef* I2C_InitStruct);3.void I2C_StructInit(I2C_InitTypeDef* I2C_InitStruct);4.void I2C_Cmd(I2C_TypeDef* I2Cx, FunctionalState NewState);5.void I2C_DMACmd(I2C_Type…...

十八、Rust gRPC 多 proto 演示
十八、Rust gRPC 多 proto 演示 网上及各官方资料,基本是一个 proto 文件,而实际项目,大多是有层级结构的多 proto 文件形式,本篇文章 基于此诉求,构建一个使用多 proto 文件的 rust grpc 使用示例。 关于 grpc 的实现…...

【Linux】Linux64位环境下编译32位报错skipping incompatible的解决办法
本文首发于 ❄️慕雪的寒舍 问题 如题,当我尝试在wsl2的ubuntu中使用-m32选项编译32位程序的时候,出现了下面的两种报错 ❯ g -m32 test.cpp -o test1 && ./test1 In file included from test.cpp:1: /usr/include/stdio.h:27:10: fatal error…...

vue指令v-model
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>vue指令v-model</title> </head>…...

CentOS安装MySQL数据库
一、更新yum源 #下载对应repo文件 wget -O CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-8.repo #清除缓存 yum clean all #生成新缓存 yum makecache #更新 yum update -y 二、安装MySQL #获取源 wget http://repo.mysql.com/mysql80-community-release-el7-3.…...

从B2B转向B2B2C模式:工业品牌史丹利百得的转型历程
图片来源:Twitter 在当今数据驱动的营销环境中,企业努力更好了解客户,并在整个客户旅程中提供个性化体验。史丹利百得(Stanley Black & Decker)是一家领先的工具和工业设备供应商,近年来开始重大转型。…...
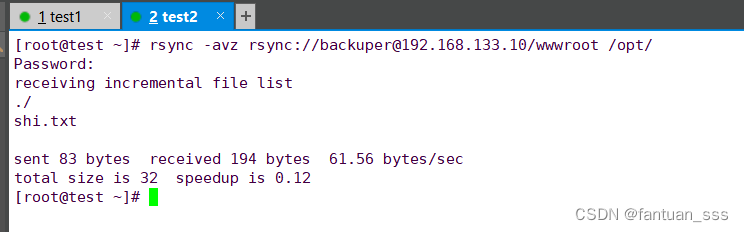
Redis群集模式和rsync远程同步
一、Redis群集模式 1.1 概念 1.2 作用 1.2.1 Redis集群的数据分片 1.2.2 Redis集群的主从复制模型 1.3 搭建Redis 群集模式 1.3.1 开启群集功能 1.3.2 启动redis节点 1.3.3 启动集群 1.3.4 测试群集 二、rsync远程同步 2.1 概念 2.2 同步方式 2.3 备份的方式 2.4…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
