组合数(费马小定理, 快速幂)
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(109+7)的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1使用快速幂求解a!,用费马小定理求解后面的逆元
代码:
#include <iostream>using namespace std;typedef long long ll;const int N = 1e5 + 10, mod = 1e9 + 7;ll n, a, b;
ll fact[N], ifact[N];ll qmi(ll a, ll b) {ll res = 1;while (b) {if (b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}void init() {fact[0] = 1;ifact[0] = 1;for (int i = 1; i < N; i ++ ) {fact[i] = fact[i - 1] * i % mod;ifact[i] = ifact[i - 1] * qmi(i, mod - 2) % mod;}
}int main() {init();cin >> n;while (n -- ) {cin >> a >> b;cout << (fact[a] * ifact[b]) % mod * ifact[a - b] % mod << endl;}
}相关文章:
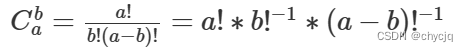
组合数(费马小定理, 快速幂)
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(1097)的值。 输入格式 第一行包含整数 n。 接下来 n 行,每行包含一组 a 和 b。 输出格式 共 n 行,每行输出一个询问的解。 数据范围 1≤n≤10000, 1≤…...

VMware Esxi安装群辉系统
群晖的网络存储产品具有强大的操作系统,提供了各种应用程序和服务,包括文件共享、数据备份、多媒体管理、远程访问等。用户可以通过简单直观的界面来管理他们的存储设备,并且可以根据自己的需求扩展设备的功能。总的来说,群晖的产…...

arm交叉编译器工具
下载地址: Builds & Downloads | Linaro 进入首页后,点击" GNU Toolchain Integration Builds" 有以下版本: 根据自己的选择下载对应的版本,本例选择14.0-2023.06-1 根据板端对应的版本选择相应的下载 比如下载3…...

Dajngo -- 表单
表单 form 此后的 app 名以 polls 为例 <h1>{{ question.question_text }}</h1>{% if error_message %} <p> <strong>{{ error_message }}</strong> </p> {% endif %}<form action"{% url polls:vote question.id %}" method…...
NIO基础知识
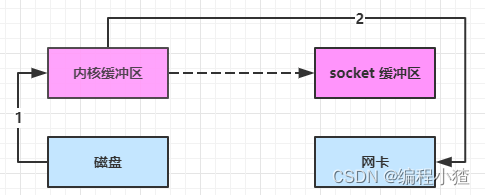
在学习Netty之前先要学习一下NIO相关的知识,因为Netty是基于NIO搭建的一套网络编程框架。 一. NIO 基础 non-blocking io 非阻塞 IO 1. 三大组件 1.1 Channel & Buffer channel 有一点类似于 stream,它就是读写数据的双向通道,可以从…...

C语言正则表达式 regnext regreplace regreplaceAll
由于C语言的正则表达式API相对比较简易.默认API只有regcomp/regerror/regexec/regfree这些函数.相对于其他的高级语言中正则表达式所所能实现的功能(如:查找/替换)有所欠缺.所以想着自己写下一些需要的函数以备后续需要使用. #ifndef _E_REGEX_INCLUDE #define _E_REGEX_INCLU…...
使用aspose相关包将excel转成pdf 并导出
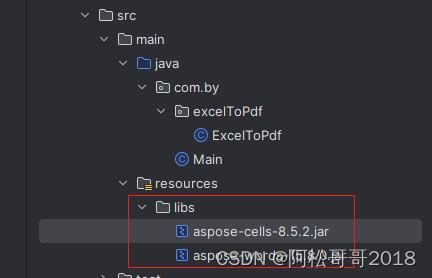
SpringBoot 项目 基于aspose相关jar包 将excel 转换成pdf 导出 1、依赖的jar包 , jar获取链接 aspose相关三方jar ,下载解压后,在项目路径下建一个libs包,然后将下图两个jar 拷贝至刚新建的libs目录中 2、pom.xml中加入maven引入 <depend…...

按关键字搜索商品API接口搜索关键字,显示商品总数,标题,图片,优惠价参数等
按关键字搜索商品API接口通常用于根据关键字搜索商品,并返回商品的相关信息。以下是一个示例,说明如何使用Python调用按关键字搜索商品API接口。 item_search-按关键字搜索淘宝商品 公共参数 API接口请求地址:调用key 名称类型必须描述keyString是调用…...
网络基础知识入门
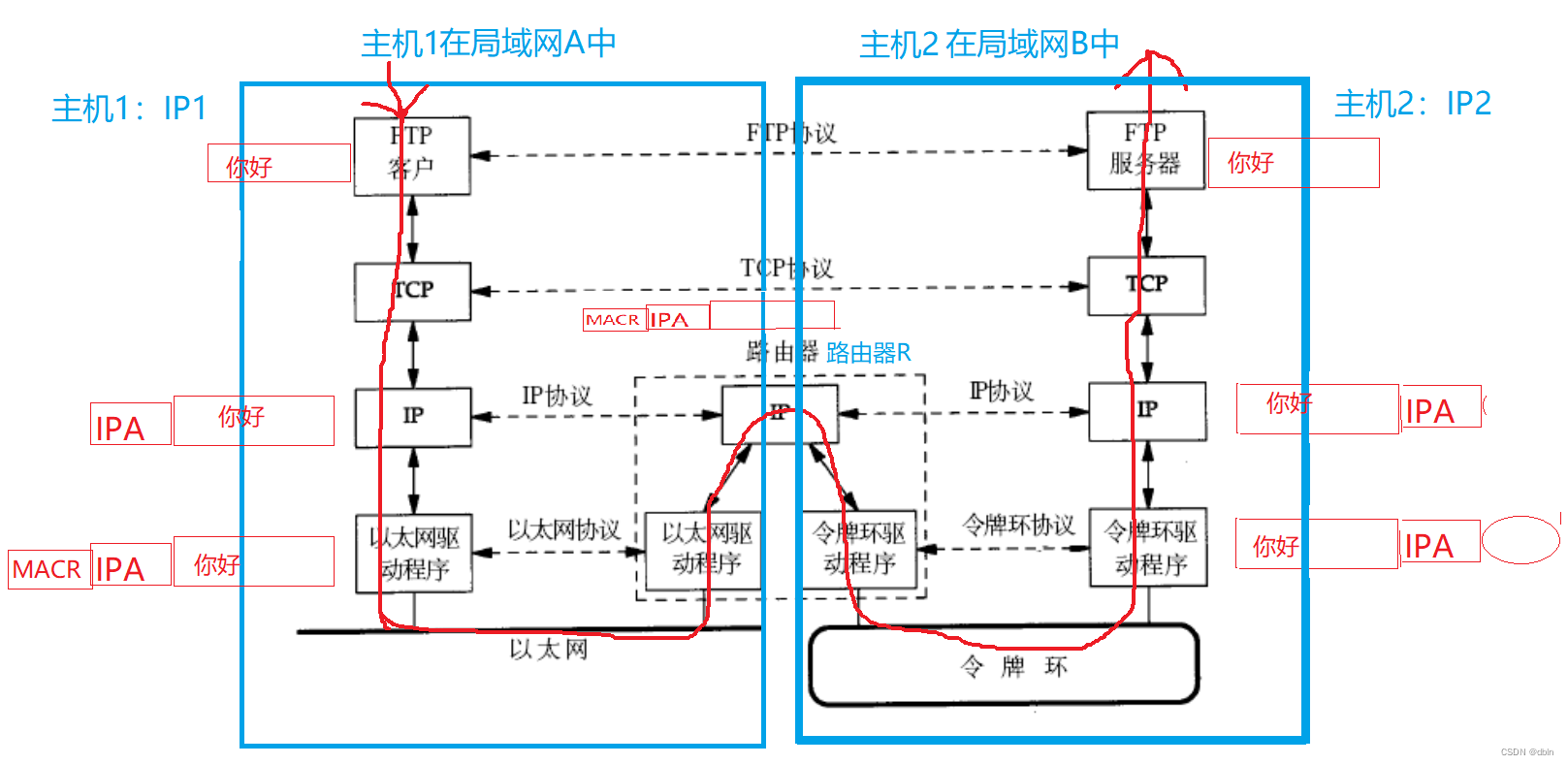
目录 一、局域网与广域网 1、局域网 2、广域网 二、协议 1、概念 2、协议的理解 3、协议的分层 1、分层 2、OSI七层模型 三、网络传输基本流程 1、报头 2、局域网通信原理 3、跨网络传输流程 四、IP地址和MAC地址 1、IP地址 2、MAC地址 3、两者的区别 一、局域…...

D435i发布的话题学习
参考自https://blog.csdn.net/sinat_16643223/article/details/136406602?spm1001.2014.3001.5502 这里整理一下D435i庞大的topic话题数据。 根据算法来说的话,vins-fusion需要双目灰度图像的话题: camera/infra1/image_rect_raw 和camera/infra2/image…...

Springboot启动过程
加载配置:Spring Boot会加载应用程序的配置文件,包括application.properties或application.yml等。这些配置文件中包含了应用程序的各种配置信息,如数据库连接、端口号等。 创建Spring容器:Spring Boot会创建一个Spring容器&…...

网络安全之命令注入
漏洞原理: 应用系统设计需要给用户提供指定的远程命令操作的接口,比如:路由器,防火墙,入侵检测等设备的web管理界面。一般会给用户提供一个ping操作的web界面 用户从web界面输入目标IP,提交后台会对改IP地…...
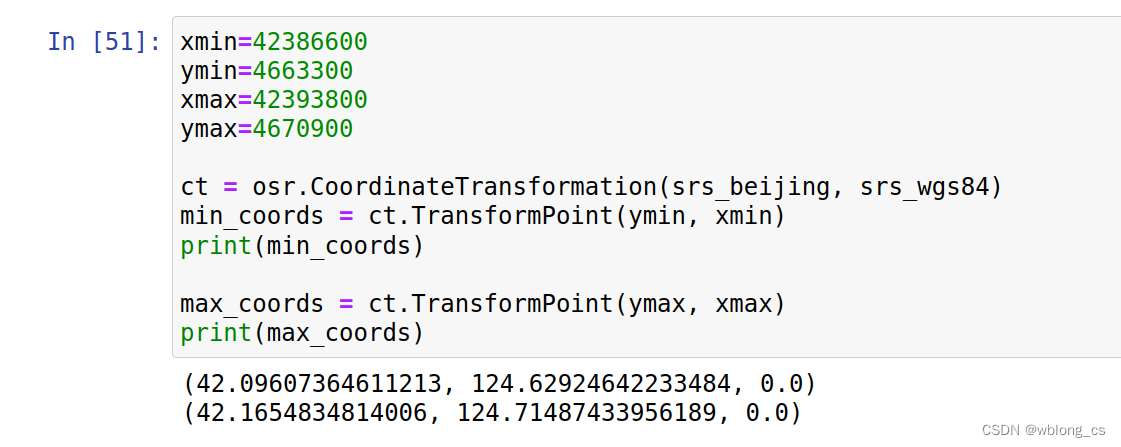
使用GDAL进行简单的坐标系转换
使用GDAL进行简单的坐标系转换 使用python GDAL进行简单的坐标系转换,暂时不考虑不同基准坐标系转换的精度问题。 安装环境 使用UbuntuAnaconda python 环境 conda install gdal 定义坐标系 from osgeo import gdal from osgeo import osrsrs_wgs84 osr.Spati…...

【AIGC调研系列】AI大模型结合迁移学习进行微调的应用
AI大模型结合迁移学习进行微调的应用主要体现在通过预训练模型快速适应新任务,提高模型性能和准确性。迁移学习允许我们利用在其他任务上学到的知识来加速新任务的学习过程,从而减少对大量标注数据的依赖,提高训练效率[1][2][3]。在AI领域&am…...

低代码革新:软件开发的未来潜力与创新路径探索
过去的一年,挑战与机遇并存。人们一边忧虑市场经济下行所带来的新的增长难题、裁员危机,一边惊叹于AIGC、量子技术等领域不断涌现新的创新成果。 时代发生了改变,传统“互联网”的模式已走入尾声,新一轮的科技革命与产业变革正在到…...

AI智能校色解决方案,专业级画质提升
由于拍摄环境、设备性能以及编辑经验等多种因素的影响,视频画质往往难以达到理想状态。这时,一款高效、智能的校色解决方案就显得尤为重要。美摄科技凭借深厚的图像处理技术和AI算法研发实力,推出了全新的AI智能校色解决方案,助力…...

面试算法-148-轮转数组
题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,…...
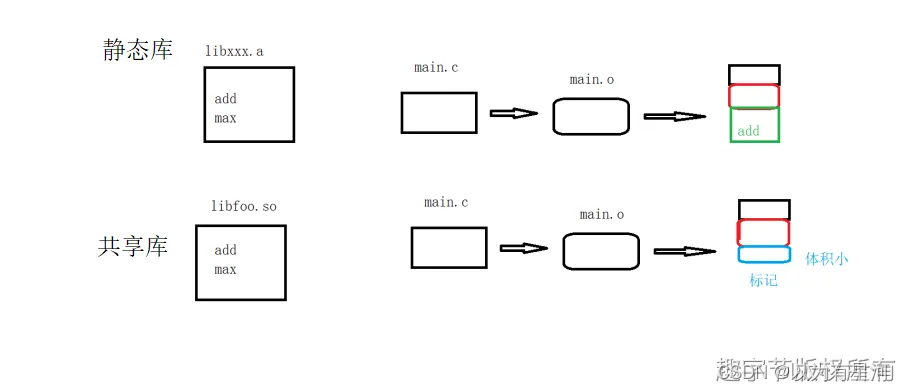
Linux——静态库 共享库
1.库文件 1).库文件 库是一组预先编译好的方法的集合; Linux系统存储库的位置一般在/lib 和 /usr/lib (64位系统/usr/lib64) 库的头文件放在/usr/include 2).库的分类 静态库:libxxx.a(命名规则) 共享库:libxxx.so(命名规则) 3).准备文件: //add.c int add(int x,int y) { re…...
基于Spring Boot+Vue的在线拍卖系统
随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单管理、…...
——SBP的Bundle写操作生成)
Unity构建详解(6)——SBP的Bundle写操作生成
以下三个操作实际上是为了得到构建Bundle需要的其他参数,最关键的Bundle组装参数在上文已经说过了,至于这三个操作的具体细节不用过于追究,一般不怎么会取修改。 这些参数采用命令模式被封装起来,这是常见的参数非常多的时候的处…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
