全自动封箱机的工作原理:科技与效率的完美结合
随着科技的不断发展,越来越多的自动化设备走进了我们的日常生活和工业生产中。其中,全自动封箱机作为物流包装领域的重要一环,凭借其高效、精准的工作性能,正逐渐成为提升生产效率、降低劳动成本的得力助手。星派就来与大家深入探讨一下全自动封箱机的工作原理以及它如何成为科技与效率完美结合的典范。
全自动封箱机的工作原理并不复杂,但其中蕴含的科技含量却不容小觑。它的工作流程大致可以分为以下几个步骤:
纸箱定位与传送:全自动封箱机首先通过传送带将待封口的纸箱输送到指定位置。这一过程中,机器会利用光电传感器等装置,确保纸箱的准确定位,为后续封口操作提供坚实基础。

自动开箱与调整:当纸箱到达指定位置后,封箱机会自动进行开箱操作。这一步骤中,机器会根据纸箱的大小和形状,自动调整开箱机构,确保纸箱的开口大小合适,便于后续封箱。
胶带粘贴与封口:在完成开箱调整后,全自动封箱机会自动将预先切好的胶带粘贴在纸箱的开口处。这一过程中,封箱机会通过精确控制胶带的长度和粘贴位置,确保封口的牢固性和美观性。
封口压实与检测:在胶带粘贴完成后,封箱机会对封口进行压实操作,确保胶带与纸箱紧密结合。同时,机器还会通过自检系统对封口质量进行检测,确保每个纸箱的封口都符合标准。
成品输出与统计:完成封口的纸箱会被传送带输出到指定位置。同时,全自动封箱机还会对生产过程中的各项数据进行统计和分析,为生产管理和优化提供有力支持。

全自动封箱机之所以能成为科技与效率完美结合的典范,其关键在于以下几点:
高精度控制:全自动封箱机采用了先进的控制系统和传感器技术,能够实现对纸箱位置的精确定位、对胶带长度的精确控制等,确保了封口的质量和效率。
高效生产能力:相比于传统的手工封箱方式,全自动封箱机具有更高的生产效率。一台机器可以替代多个工人同时作业,大大提升了生产线的整体效率。
降低劳动成本:全自动封箱机的使用可以大幅度减少人工封箱所需的人力成本,同时降低因人为因素造成的封口质量不稳定问题。
智能化管理:全自动封箱机配备了先进的自检系统和数据分析功能,可以实现对生产过程的实时监控和数据分析,为企业的生产管理和优化提供了有力支持。
全自动封箱机作为科技与效率完美结合的典范,正以其高效、精准、智能的工作性能,为现代工业生产带来了革命性的变革。随着科技的不断进步和市场的不断拓展,我们有理由相信,全自动封箱机将在未来的物流包装领域中发挥更加重要的作用。
相关文章:

全自动封箱机的工作原理:科技与效率的完美结合
随着科技的不断发展,越来越多的自动化设备走进了我们的日常生活和工业生产中。其中,全自动封箱机作为物流包装领域的重要一环,凭借其高效、精准的工作性能,正逐渐成为提升生产效率、降低劳动成本的得力助手。星派就来与大家深入探…...
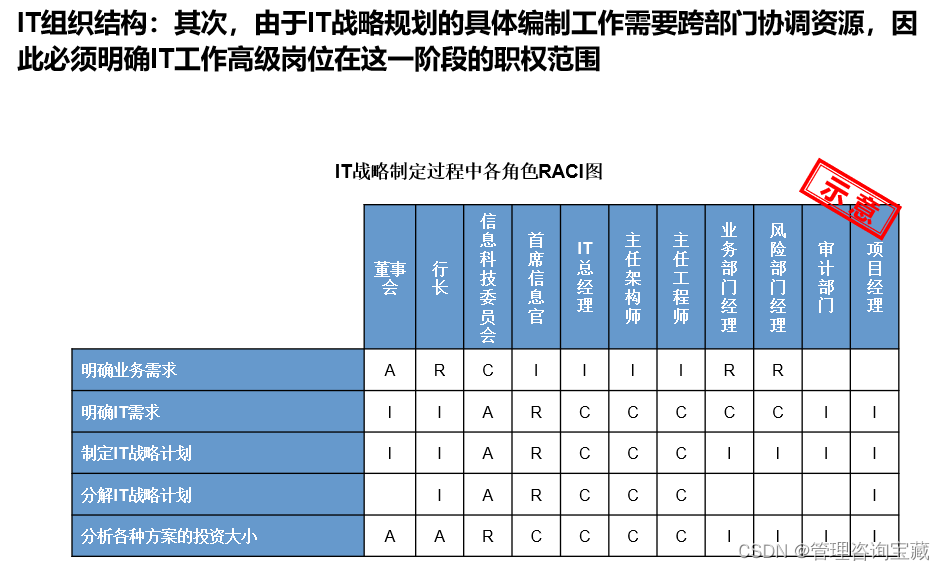
【管理咨询宝藏48】AA银行信息科技提升分析报告
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏48】AA银行信息科技提升分析报告 【格式】PPT版本,可编辑 【关键词】战略规划、商业分析、管理咨询 【强烈推荐】这是一套市面上非常…...

循序表实战——基于循序表的通讯录
前言:本篇文章主要是利用顺序表作为底层, 实现一个通讯录。偏向于应用, 对于已经学习过c的友友们可能没有难度了已经。没有学习过c的友友, 如果顺序表不会写, 或者说没有自己实现过, 请移步学习顺序表相关内…...

Java编程规范及最佳实践
文章目录 一、命名规范二、代码风格规范三、注释规范四、推荐的编程实践五、类和接口六、异常处理七、可见性八、并发九、代码复用十、代码组织和模块化十一、Java集合框架十二、输入验证十三、资源管理十四、文档和注释十五、测试和代码质量十六、代码可读性十七、性能优化十八…...

90天玩转Python—07—基础知识篇:Python中运算符详解
90天玩转Python系列文章目录 90天玩转Python—01—基础知识篇:C站最全Python标准库总结 90天玩转Python--02--基础知识篇:初识Python与PyCharm 90天玩转Python—03—基础知识篇:Python和PyCharm(语言特点、学习方法、工具安装) 90天玩转Python—04—基础知识篇:Pytho…...

C语言 位域
C 语言的位域(bit-field)是一种特殊的结构体成员,允许我们按位对成员进行定义,指定其占用的位数。 如果程序的结构中包含多个开关的变量,即变量值为 TRUE/FALSE,如下: struct {unsigned int w…...

【LeetCode热题100】【技巧】颜色分类
题目链接:75. 颜色分类 - 力扣(LeetCode) 只需排序三种,可以记录0和1的个数,然后直接原地赋值 class Solution { public:void sortColors(vector<int> &nums) {int zero 0, one 0;for (auto &num: n…...
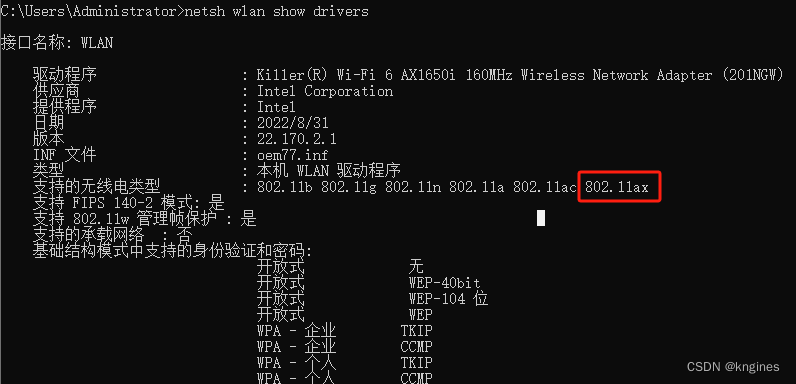
笔记本电脑win7 Wireless-AC 7265连不上wifi6
1.背景介绍 旧路由器连接人数有限,老旧,信号不稳定更换了新路由器,如 TL-XDR5430易展版用户电脑连不上新的WIFI网络了,比较着急 核心问题:有效解决笔记本连接wifi上网问题,方法不限 2.环境信息 Windows…...
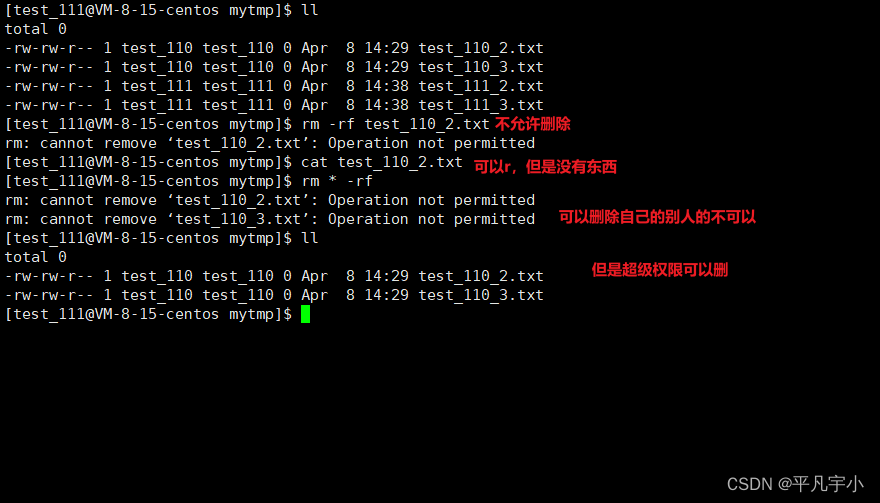
Linux gcc day5粘滞位
粘滞位 背景:一定时在一个公共目录(root创建)下。进行临时文件的操作 Linux系统中有很多人,我们需要在一个公共目录下,进行临时文件的操作(增删查改) 创建一个根目录下的dir(mytmp…...

单片机按键消抖常用的软硬件方法
一:什么是开关抖动? 当我们按下按钮或拨动开关或微动开关时,两个金属部件会接触以短路电源。但它们不会立即连接,而是金属部件在实际稳定连接之前连接和断开几次。释放按钮时也会发生同样的事情。这会导致误触发或多次触发&#…...
)
钉钉自建应用-下载excel(h5)
由于不同手机对于文件下载有不同的支持,而且文件路径也不一样,找起来十分的麻烦。所以,最好是找到一个都支持的方法。还好,钉钉官网提供了网盘,我们可把文件保存到钉钉自带的网盘,这样方便查找。 这里需要…...

用二八定律分析零售数据,不就更直观了吗?
20%的商品贡献了80%的销售金额,你会不会想知道这些商品的销售金额、毛利、销售金额累计占比、毛利累计占比,会不会想知道这些商品在各个门店的销售表现?看是否能进一步提高销售金额,提高毛利。这样的报表该怎么做?奥威…...
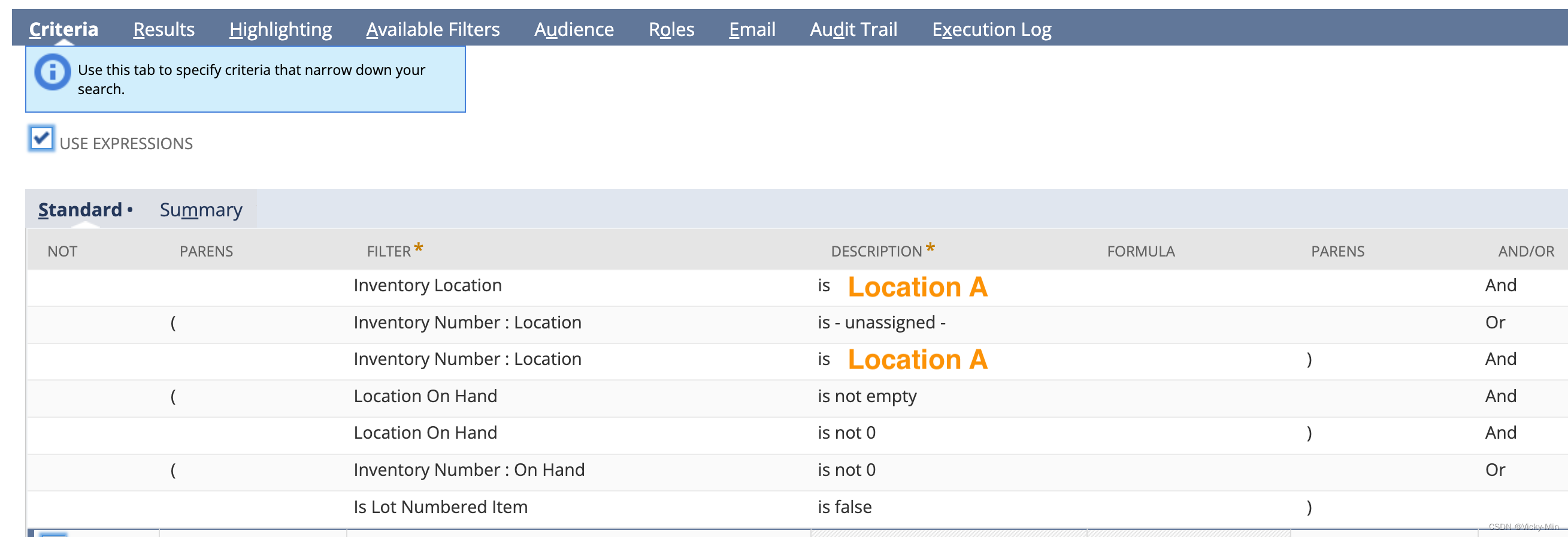
NetSuite Saved Search-当前库存快照查询报表(二)
之前第一篇文章我们说明了,如何利用Saved Search来制作一个能够显示批次物料与非批次物料的Lot信息以及On Hand在手数量的“当前库存快照查询报表”,但是当用户提出“我们能否再加上批次物料的效期”需求时,我们原有的Saved Search并不能达到…...

【JavaSE】接口 详解(上)
前言 本篇会讲到Java中接口内容,概念和注意点可能比较多,需要耐心多看几遍,我尽可能的使用经典的例子帮助大家理解~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 目录 前言 接口 语法…...

嵌入式C基础——循环队列 ringbuffer 讲解
本期主题: 讲解ARRAY_SIZE的作用以及定义,还有一个踩坑分析 往期链接: 数据结构系列——先进先出队列queue数据结构系列——栈 stackLinux内核链表零长度数组的使用inline的作用嵌入式C基础——ARRAY_SIZE使用以及踩坑分析 目录 1. Ringbuff…...

【动态规划-状态压缩dp】【蓝桥杯备考训练】:毕业旅行问题、蒙德里安的梦想、最短Hamilton路径、国际象棋、小国王【已更新完成】
目录 1、毕业旅行问题(今日头条2019笔试题) 2、蒙德里安的梦想(算法竞赛进阶指南) 3、最短Hamilton路径(《算法竞赛进阶指南》&模板) 4、国际象棋(第十二届蓝桥杯省赛第二场C A组/B组&#…...

全坚固笔记本丨工业笔记本丨三防笔记本相较于普通笔记本有哪些优势?
三防笔记本和普通笔记本在设计和性能方面存在显著差异,三防笔记本相较于普通笔记本具备以下优势: 三防笔记本通常采用耐磨、耐摔的材料,并具有坚固的外壳设计,能够承受恶劣环境和意外碰撞,有效保护内部组件不受损坏。相…...

机房搬迁方案
一、项目背景 随着XX公司业务的不断扩展,现有的机房设备已经无法满足日益增长的数据处理需求。同时,考虑到现有机房的设施老化及潜在的安全隐患,XX公司决定进行机房搬迁。本次搬迁旨在确保业务连续性、数据安全性以及新机房的高效运营。 二…...

推动科技创新润德生物邀您到场参观2024第13届生物发酵展
参展企业介绍 山东润德生物科技有限公司成立于2014年10月17日,是一家围绕生物制品的研发、生产、营销、国际贸易、技术服务为核心业务的国家高新技术企业,近年来荣获国家制造业单项冠军示范企业、国家级绿色工厂、国家知识产权优势企业、国家工业产品绿…...

如何在JavaScript中提高性能
在JavaScript中提高性能是一个涉及多个方面的任务,包括代码优化、数据结构选择、异步编程、避免全局查找、内存管理等。以下是一些关键的策略和技巧,可以帮助你提高JavaScript代码的性能: 1. 优化循环 使用for循环代替forEach,特…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
