【动态规划-状态压缩dp】【蓝桥杯备考训练】:毕业旅行问题、蒙德里安的梦想、最短Hamilton路径、国际象棋、小国王【已更新完成】
目录
1、毕业旅行问题(今日头条2019笔试题)
2、蒙德里安的梦想(算法竞赛进阶指南)
3、最短Hamilton路径(《算法竞赛进阶指南》&模板)
4、国际象棋(第十二届蓝桥杯省赛第二场C++ A组/B组)
5、小国王(《信息学奥赛一本通》 SGU223)
1、毕业旅行问题(今日头条2019笔试题)
小明目前在做一份毕业旅行的规划。
打算从北京出发,分别去若干个城市,然后再回到北京,每个城市之间均乘坐高铁,且每个城市只去一次。
由于经费有限,小明希望能够通过合理的路线安排尽可能的省些路上的花销。
给定一组城市和每对城市之间的火车票的价钱,找到每个城市只访问一次并返回起点的最小车费花销。
注意:北京为 1 号城市。
输入格式
第一行包含一个正整数 n,表示城市个数。
接下来输入一个 n 行 n 列的矩阵,表示城市间的车票价钱。
输出格式
输出一个整数,表示最小车费花销。
数据范围
1<n≤20,包括北京
车票价格均不超过 1000 元。
输入样例:
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
输出样例:
13
说明
共 4 个城市,城市 1 和城市 1 的车费为0,城市 1 和城市 2 之间的车费为 2,城市 1 和城市 3 之间的车费为 6,城市 1 和城市 4 之间的车费为 5,以此类推。
假设任意两个城市之间均有单程票可买,且价格均在 1000 元以内,无需考虑极端情况。
思路:
经典的状态压缩求最短路问题,每个城市只有两个状态:去过或者没去过,去过则为1,没去过则为0

代码:
#include<bits/stdc++.h>using namespace std;int n; const int N=20,M=1<<20;int w[N][N];int f[M][N];//M表示状态的压缩,N代表最后到哪一个城市了 int main()
{cin>>n;memset(f,0x3f,sizeof f);//每个状态为正无穷,表示还没取min for(int i=0;i<n;i++){for(int j=0;j<n;j++){scanf("%d",&w[i][j]);}}f[1][0]=0;//初始的状态(需要费用为0) //从1开始表示北京已经去过了 (二进制表示为000.....1) for(int i=1;i<1<<n;i++)//(1<<n)-1就是111....1//例如n==5的时候,1<<5就是100000,减去1就是11111 {for(int j=0;j<n;j++)//北京开始 {//这个状态下(终点为j,状态为i) if(i>>j&1)//(i>>j表示要到第j个城市,这个状态的j位就要是1(否则到不了)) {for(int k=0;k<n;k++)//从第k个城市转移过来{if((i-(1<<j))>>k&1)//i中减去第j个城市后还包含k//说明这个状态到过k,可以从k转移过来f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]); } }}}int res=1<<31-1;for(int i=1;i<n;i++){res=min(res,f[(1<<n)-1][i]+w[i][0]);}cout<<res;return 0;
} 2、蒙德里安的梦想(算法竞赛进阶指南)
求把 N×M 的棋盘分割成若干个 1×2 的长方形,有多少种方案。
例如当 N=2,M=4 时,共有 5 种方案。当 N=2,M=3,时,共有 3 种方案。
如下图所示:
![]()
输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 N 和 M。
当输入用例 N=0,M=0 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
1≤N,M≤11
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例:
1
0
1
2
3
5
144
51205
思路:
先放置完横着放的,之后竖着放的方法就是固定的
一个重要的任务就是判断放置的方法是否合法
基本框架:

预处理:
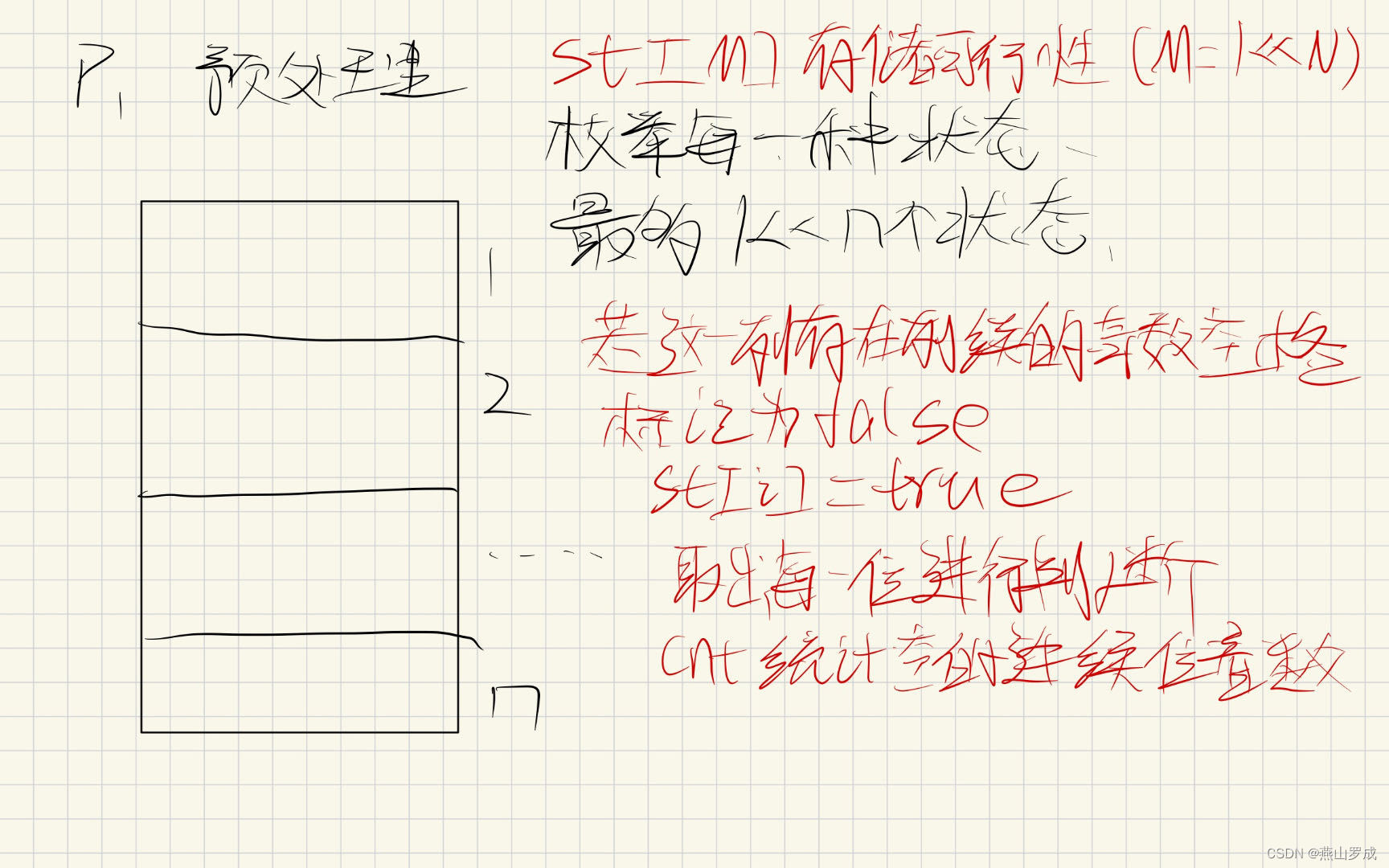
dp:

代码:
#include<bits/stdc++.h>using namespace std;const int N=12;
const int M=1<<11;int n,m;long long f[N][M];//第i列的状态为M ,j表示出头的方格数量 bool st[M];//用来表示某一种状态是否合法 int main()
{while(cin>>n>>m,n || m){memset(f,0,sizeof f);//开始预处理for(int i=0;i<1<<n;i++)//枚举每一种状态 {int cnt=0;//记录连续的空格数量 st[i]=true; for(int j=0;j<n;j++){if(i>>j&1)//这个位置不是空格 {if(cnt&1)st[i]=false;//这个位置之前的连续空格数量是奇数,不合法 cnt=0;}else cnt++;}if(cnt&1)st[i]=false; }f[0][0]=1;//第0列没有上一列,所以没有戳出来的//小方块里什么都没有放,只有这一种状态 for(int i=1;i<=m;i++)//枚举列 {for(int j=0;j<1<<n;j++)//枚举这一列的状态 {for(int k=0;k<1<<n;k++)//枚举上一列的状态 {if(((j&k)==0) && st[j|k])//(k列加上j列向后伸的格子后要合法){f[i][j]+=f[i-1][k];}}}} cout<<f[m][0]<<endl;}return 0;
}3、最短Hamilton路径(《算法竞赛进阶指南》&模板)
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x],并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤1e7
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18思路:
状态压缩dp模板
代码:
#include<bits/stdc++.h>using namespace std;const int N=20,M=1<<20;int n;int w[N][N];int f[M][N];int main()
{int n;cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){scanf("%d",&w[i][j]);}}//状态压缩dp memset(f,0x3f,sizeof f);//初始为0f[1][0]=0;//i==1表示第一个点已经走了,j==0表示目前在第一个点 //从0000.。。1开始 for(int i=1;i<1<<n;i++){//从起点0开始 for(int j=0;j<n;j++){//只有i包含j这个点,才能从i这个状态转移到终点为j的状态 if(i>>j&1){//f[i][k]---k-jfor(int k=0;k<n;k++){if((i-(1<<j))>>k&1){//(用不包含j点的状态来转移)f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);}}}}}int res=1<<31-1;//for(int i=1;i<n;i++)//{// res=min(res,f[(1<<n)-1][i]);//}//cout<<res<<endl;//标明了终点是n-1,所以说直接选终点是n-1的情况 cout<<f[(1<<n)-1][n-1];return 0;
}4、国际象棋(第十二届蓝桥杯省赛第二场C++ A组/B组)
众所周知,“八皇后” 问题是求解在国际象棋棋盘上摆放 8 个皇后,使得两两之间互不攻击的方案数。
已经学习了很多算法的小蓝觉得 “八皇后” 问题太简单了,意犹未尽。作为一个国际象棋迷,他想研究在 N×M 的棋盘上,摆放 K 个马,使得两两之间互不攻击有多少种摆放方案。
由于方案数可能很大,只需计算答案除以 1000000007 (即 1e9+7) 的余数。
如下图所示,国际象棋中的马摆放在棋盘的方格内,走 “日” 字,位于 (x,y)格的马(可以攻击 (x+1,y+2)、(x+1,y−2)、(x−1,y+2)、(x−1,y−2)、(x+2,y+1)、(x+2,y−1)、(x−2,y+1) 和 (x−2,y−1) 共 8 个格子。
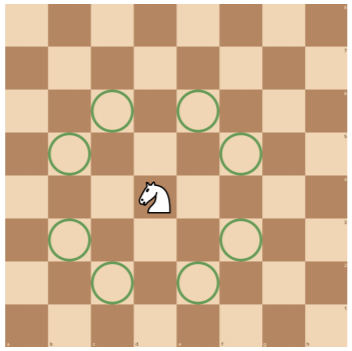
输入格式
输入一行包含三个正整数 N,M,K分别表示棋盘的行数、列数和马的个数。
输出格式
输出一个整数,表示摆放的方案数除以 1000000007(即 1e9+7) 的余数。
数据范围
对于 5%5% 的评测用例,K=1;
对于另外 10%10% 的评测用例,K=2;
对于另外 10%10% 的评测用例,N=1;
对于另外 20%20% 的评测用例,N,M≤6,K≤5;
对于另外 25%25% 的评测用例,N≤3,M≤20,K≤12;
对于所有评测用例,1≤N≤6,1≤M≤100,1≤K≤20。
输入样例1:
1 2 1
输出样例1:
2
输入样例2:
4 4 3
输出样例2:
276
输入样例3:
3 20 12
输出样例3:
914051446思路:
枚举思路:

代码:
#include<bits/stdc++.h>using namespace std;
typedef long long LL;
const int N = 110,M=6,MOD=1e9+7;
int f[N][1<<M][1<<M][21];
int n,m,k;
int get_count(int x)//返回x的二进制有多少个1
{int res=0;while(x){res++;x-=(x&-x);}return res;
}
int main()
{scanf("%d%d%d",&n,&m,&k);f[0][0][0][0]=1;//状态初始化:第0行时,状态只能是0,只能是放0个马//5层循环比较乱,把图画出来,照着图写for(int i=1;i<=m;i++){for(int c=0;c<1<<n;c++){for(int a=0;a<1<<n;a++){if((c&(a<<2))||(a&(c<<2))) continue;for(int b=0;b<1<<n;b++){if(b&(a<<2)||a&(b<<2)) continue;if(b&(c<<1)||c&(b<<1)) continue;int t=get_count(b);for(int j=t;j<=k;j++)f[i][a][b][j]=(f[i][a][b][j]+f[i-1][c][a][j-t])%MOD;//对应集合划分,枚举j,f[i-1][c][a][j-t]都能到达f[i][a][b][j]}}}}int res=0;for(int a=0;a<1<<n;a++){for(int b=0;b<1<<n;b++){res=(res+f[m][a][b][k])%MOD;//m,k固定,a,b随意}}printf("%d",res);return 0;
}
5、小国王(《信息学奥赛一本通》 SGU223)
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 n 和 k。
输出格式
共一行,表示方案总数,若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n**2
输入样例:
3 2
输出样例:
16思路:

代码:
#include<bits/stdc++.h>using namespace std;typedef long long LL;const int N = 11, M = 1 << N, C = N * N;int n, m, K;
LL f[N][C][M];
int cnt[M];
vector<int> legal_state;
vector<int> state_trans[M];bool check(int state)
{return !(state & state >> 1);
}
int count(int state)
{int res=0;while(state){res++;state-=state & -state;}return res;
}
int main()
{cin >> n >> K;//预处理所有合法状态for (int st = 0; st < 1 << n; ++ st)//检查当前状态是否合法if (check(st))legal_state.push_back(st),cnt[st] = count(st);m = legal_state.size();//预处理所有合法状态的合法转移for (auto cur_st: legal_state)for (auto to_st: legal_state)if (!(cur_st & to_st) && check(cur_st | to_st))//上下不相邻且纵坐标也不相邻state_trans[cur_st].push_back(to_st);//动态规划f[0][0][0] = 1;for (int i = 1; i <= n; ++ i)for (int j = 0; j <= K; ++ j)for (auto &state: legal_state)for (auto &pre_st: state_trans[state])if (j - cnt[state] >= 0)f[i][j][state] += f[i - 1][j - cnt[state]][pre_st];//统计目标状态的所有方案数LL res = 0;for (auto state: legal_state) res += f[n][K][state];cout << res << endl;return 0;
}
相关文章:

【动态规划-状态压缩dp】【蓝桥杯备考训练】:毕业旅行问题、蒙德里安的梦想、最短Hamilton路径、国际象棋、小国王【已更新完成】
目录 1、毕业旅行问题(今日头条2019笔试题) 2、蒙德里安的梦想(算法竞赛进阶指南) 3、最短Hamilton路径(《算法竞赛进阶指南》&模板) 4、国际象棋(第十二届蓝桥杯省赛第二场C A组/B组&#…...

全坚固笔记本丨工业笔记本丨三防笔记本相较于普通笔记本有哪些优势?
三防笔记本和普通笔记本在设计和性能方面存在显著差异,三防笔记本相较于普通笔记本具备以下优势: 三防笔记本通常采用耐磨、耐摔的材料,并具有坚固的外壳设计,能够承受恶劣环境和意外碰撞,有效保护内部组件不受损坏。相…...

机房搬迁方案
一、项目背景 随着XX公司业务的不断扩展,现有的机房设备已经无法满足日益增长的数据处理需求。同时,考虑到现有机房的设施老化及潜在的安全隐患,XX公司决定进行机房搬迁。本次搬迁旨在确保业务连续性、数据安全性以及新机房的高效运营。 二…...

推动科技创新润德生物邀您到场参观2024第13届生物发酵展
参展企业介绍 山东润德生物科技有限公司成立于2014年10月17日,是一家围绕生物制品的研发、生产、营销、国际贸易、技术服务为核心业务的国家高新技术企业,近年来荣获国家制造业单项冠军示范企业、国家级绿色工厂、国家知识产权优势企业、国家工业产品绿…...

如何在JavaScript中提高性能
在JavaScript中提高性能是一个涉及多个方面的任务,包括代码优化、数据结构选择、异步编程、避免全局查找、内存管理等。以下是一些关键的策略和技巧,可以帮助你提高JavaScript代码的性能: 1. 优化循环 使用for循环代替forEach,特…...
)
外观模式(面子模式)
外观模式 文章目录 外观模式什么是外观模式示例 什么是外观模式 外观模式(Facade),为子系统中的一组接口提供一个一致的界面,此模式定义了一个高层接口,这个接口使得这一子系统更加容易使用 Facade 外观类 知道哪些子系统类负责处理请求,将客…...

蓝桥杯考前复习三
1.约数个数 由乘法原理可以得出: import java.util.*; public class Main{static int mod (int)1e9 7;public static void main(String[] args){Map<Integer,Integer> map new HashMap<>(); //创建一个哈希表Scanner scan new Scanner(System.in);i…...

极客时间: 用 Word2Vec, LangChain, Gemma 模拟全本地检索增强生成(RAG)
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

VBA操作Word
检查word中的字体情况 Sub ListAllFontsInDocument()Dim doc As DocumentDim rng As RangeDim char As RangeDim fontName As StringDim uniqueFonts As Collection 初始化集合用于存储唯一字体名称Set uniqueFonts New Collection 获取当前活动文档Set doc ActiveDocument …...

Linux文件IO(4):目录操作和文件属性获取
目录 1. 前言 2. 函数介绍 2.1 访问目录 – opendir 2.2 访问目录 – readdir 2.3 访问目录 – closedir 2.4 修改文件访问权限 – chmod/fchmod 2.5 获取文件属性 – stat/lstat/fstat 2.5.1 文件属性 – struct stat 2.6 文件类型 – st_mode 3. 代码练习 3.1 要求 3.2 代…...
【C语言】_文件类型,结束判定与文件缓冲区
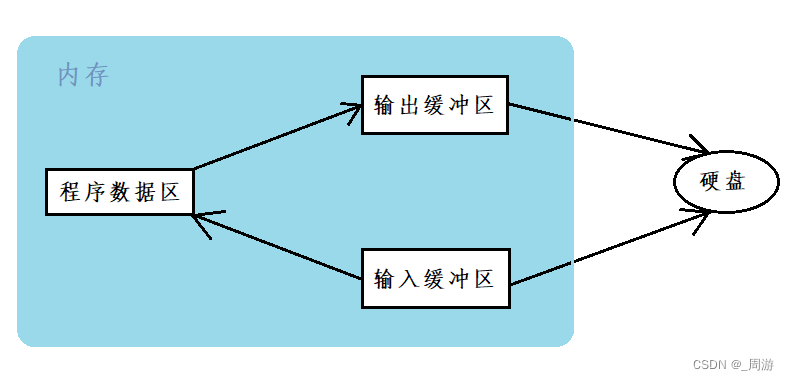
目录 1. 文本文件和二进制文件 2. 文件读取结束的判定 3. 文件缓冲区 1. 文本文件和二进制文件 根据数据的组织形式,数据文件被称为文本文件或二进制文件; 数据在内存中以二进制的形式存储,如果不加转换地输出到外存,就是二进…...
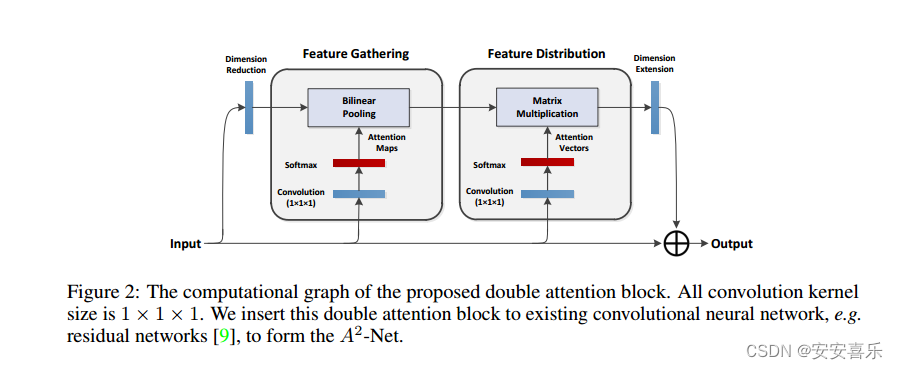
YOLOV8注意力改进方法:DoubleAttention(附代码)
原论文地址:原论文地址 DoubleAttention网络结构的优点在于,它能够有效地捕获图像中不同位置和不同特征的重要性,从而提高了图像识别和分割的性能。 论文相关内容介绍: 论文摘要:学习捕捉远程关系是图像/视频识别的…...

每日一题 --- 前 K 个高频元素[力扣][Go]
前 K 个高频元素 题目:347. 前 K 个高频元素 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 示例 1: 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2]示例 2: 输入: nums [1], k 1 输出: …...
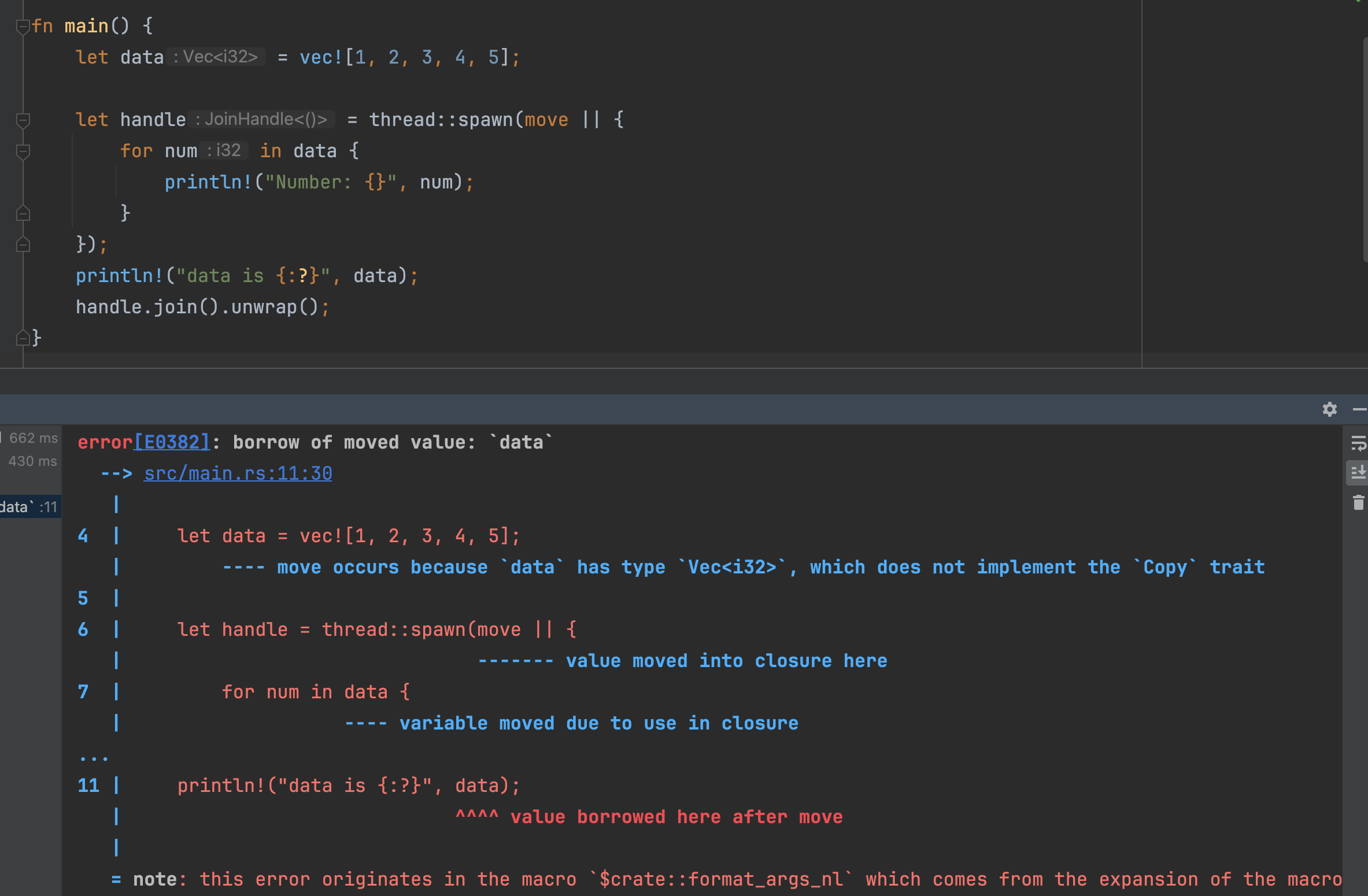
Rust所有权和Move关键字使用和含义讲解,以及Arc和Mutex使用
Rust 所有权规则 一个值只能被一个变量所拥有,这个变量被称为所有者。 一个值同一时刻只能有一个所有者,也就是说不能有两个变量拥有相同的值。所以对应变量赋值、参数传递、函数返回等行为,旧的所有者会把值的所有权转移给新的所有者&#…...
【YOLOV5 入门】——构建自己的数据集模型训练模型检验
一、准备工作 1、数据收集 图片类型数据不用多说;视频类型数据利用opencv进行抽帧保存为一张张图片,这里选取30s的名侦探柯南片段进行试验,确保环境解释器下安装了opencv(我使用的是另一个虚拟环境): im…...

MacBook 访达使用技巧【mac 入门】
快捷键 打开访达搜索窗口默认快捷键【⌥ ⌘ 空格键】可以在键盘【系统偏好设置 -> 键盘->快捷键->聚焦】修改 但是我不会去修改它,因为我不常用访达的搜索窗口,更多的是想快速打开访达文件夹窗口,可以通过第三方软件定义访达的快…...

常见溯源,反溯源,判断蜜罐手段
常见溯源,反溯源,判断蜜罐手段 1.溯源手段2.反溯源手段3.如何判断蜜罐🍯4.案例:MySQL读文件蜜罐 1.溯源手段 IP地址追踪:通过IP地址追踪可以确定攻击者的地理位置和ISP信息等;通过攻击IP历史解析记录/域名…...
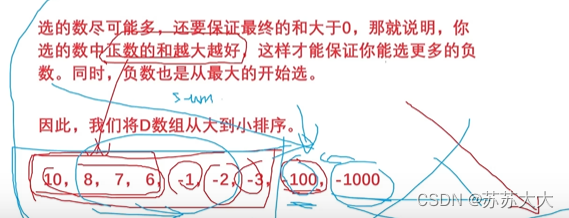
蓝桥杯刷题-09-三国游戏-贪心⭐⭐⭐
蓝桥杯2023年第十四届省赛真题-三国游戏 小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X, Y, Z (一开始可以认为都为 0 )。游戏有 n 个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i 个事件发生时会分别让 X, Y,…...
Windows编译运行TensorRT-YOLOv9 (C++)
Windows编译运行yolov9-bytetrack-tensorrt(C) 1 基础环境2 编译yolov9-bytetrack-tensorrt(1)下载yolov9-bytetrack-tensorrt源码(2)修改CMakeLists.txt(3)CMake编译 3 yolov9模型转…...
)
.NET 设计模式—简单工厂(Simple Factory Pattern)
简介 简单工厂模式(Simple Factory Pattern)属于类的创建型模式,又叫静态工厂方法模式(Static FactoryMethod Pattern),是通过一个工厂类来创建对象,根据不同的参数或条件返回相应的对象实例。这种模式隐藏…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

