滑动窗口求最大和最小
滑动窗口
要区分最小和最大滑窗,内层while循环的条件和更新结果的地方
核心:
关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。
最小滑窗
给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最小长度。
while j < len(nums)://这个while也可用fori代替判断[i, j]是否满足条件while 满足条件:不断更新结果(注意在while内更新!)i += 1 (最大程度的压缩i,使得滑窗尽可能的小)j += 1
L209长度最小的子数组
-
题目:给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
-
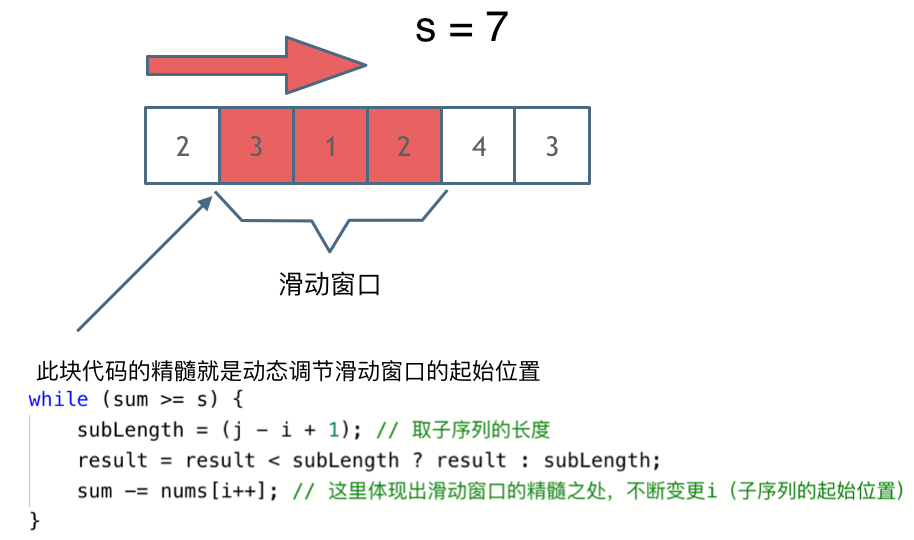
-
class Solution {// 滑动窗口public int minSubArrayLen(int s, int[] nums) {int left = 0;int sum = 0;int result = Integer.MAX_VALUE;for (int right = 0; right < nums.length; right++) {sum += nums[right];//这里要求的是最小子数组,所以这里的while是满足条件的//然后在while里面最大程度的压缩i(也就是左边界)while (sum >= s) {result = Math.min(result, right - left + 1);sum -= nums[left++];}}return result == Integer.MAX_VALUE ? 0 : result;} }
最大滑窗
给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最大长度。
while j < len(nums):判断[i, j]是否满足条件while 不满足条件:i += 1 (最保守的压缩i,一旦满足条件了就退出压缩i的过程,使得滑窗尽可能的大)不断更新结果(注意在while外更新!)j += 1
L904水果成蓝
-
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。 -
白话题目:求只包含两种元素的最长连续子序列
-
class Solution {public int totalFruit(int[] fruits) {int n = fruits.length;Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();int left = 0, ans = 0;for (int right = 0; right < n; ++right) {cnt.put(fruits[right], cnt.getOrDefault(fruits[right], 0) + 1);//注意这里的while是不满足条件的//并且这里统计的ans是在while外面进行更新的!!!!!//这个与上面的最小子数组有着本质区别while (cnt.size() > 2) {cnt.put(fruits[left], cnt.get(fruits[left]) - 1);if (cnt.get(fruits[left]) == 0) {cnt.remove(fruits[left]);}++left;}ans = Math.max(ans, right - left + 1);}return ans;} }
总结:
-
第一题让求大于某个数的最小子数组长度
-
while里面最大限度的压缩,只要满足就压缩
-
while的条件是大于某个数(即满足题意),并且while每循环一次就更新一下result的长度
-
while (sum >= s) {result = Math.min(result, right - left + 1);sum -= nums[left++];}
-
-
第二题让求最多包含两类(<=2)的最长子序列长度
-
while里面最小程度的压缩
-
while里的条件是大于2(即与题意相反),并且是while结束后进行更新长度ans
-
while (cnt.size() > 2) {cnt.put(fruits[left], cnt.get(fruits[left]) - 1);if (cnt.get(fruits[left]) == 0) {cnt.remove(fruits[left]);}++left;}ans = Math.max(ans, right - left + 1);
-
相关文章:

滑动窗口求最大和最小
滑动窗口 要区分最小和最大滑窗,内层while循环的条件和更新结果的地方 核心: 关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。 最小滑窗 给定数组 nums࿰…...

跟ChatGPT学量化,菜鸟炒股也不怕
你是一个python资深量化开发工程师,请介绍量化交易的基本框架 量化交易的基本框架包括以下几个步骤: 数据获取:获取市场数据和公司财务数据等,可以使用API接口、爬虫等方式获取。数据清洗和预处理:对获取到的数据进行清…...

扬帆优配|2600亿新能源巨头狂飙!外资唱多中国:再涨15%
全国停摆的危机,正在迫临法国。 大停工正在将法国推向风险境地。法国政府估计,当地时间3月7日,将迸发全国大型停工游行。法国总工会宣告,到时将让全法国停摆。法国担任交通业务的部长级代表克莱蒙博讷正告称,7日将成为…...
ChatGPT技术与商业模式及产业发展布局方案
文章目录模块一:概念模块二:架构模块三:技术模块四:算力模块五:体验模块六:应用模块七:商业模块八:产业模块九:建议结语主要内容: 采用模块化教学方法&#x…...

CIMCAI port ai shipping ai artificial intelligence smart port
上海人工智能独角兽中集集团高科技中集飞瞳,是全球应用落地最广,规模最大,最先进的的港航人工智能高科技企业,工业级成熟港航人工智能产品全球规模化落地应用,全球前三大船公司及港口码头应用落地。上海人工智能独角兽…...
《数据解构》HashMap源码解读
👑作者主页:Java冰激凌 📖专栏链接:数据结构 目录 了解HashMap HashMap的构造 两个参数的构造方法 一个参数的构造方法 不带参数的构造方法 哈希表初始化的长度 HashMap源码中的成员 Pt Get 了解HashMap 首先我们要明…...

Databend 开源周报 第 83 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.com 。Whats New探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。Support for WebHDFSHDFS 是大数…...
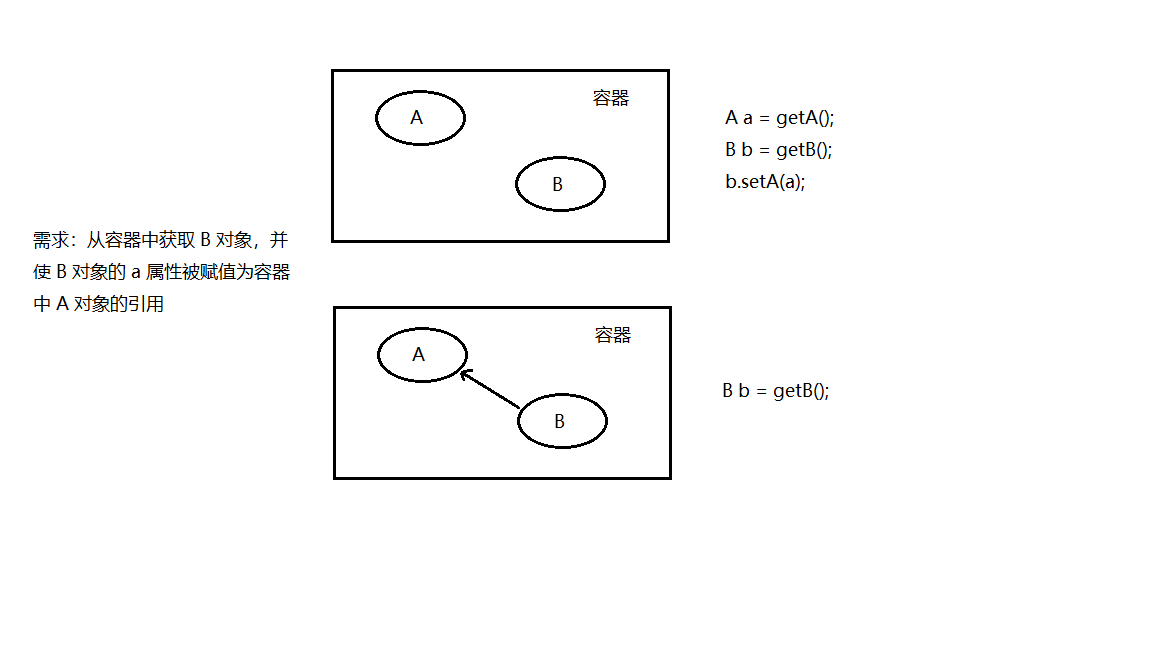
Spring | 基础
1. IOC和DI IOC:控制反转,其思想是反转资源获取的方向,传统的资源查找方式要求组件向容器发起请求查找资源,作为回应,容器适时的返回资源。而应用了 IOC 之后,则是**容器主动地将资源推送给它所管理的组件…...

windows7安装sql server 2000安装步骤 及安装过程中遇到的问题和解决方式
提示:文章写完后windows7安装sql server 2000安装步骤 及安装过程中遇到的问题和解决方式, 文章目录一、ms sql server 2000是什么?版本简介:**特点:****优点:**二、步骤1.下载安装包及Sq4补丁包2.安装 ms …...

Python 开发-批量 FofaSRC 提取POC 验证
数据来源 学习内容和目的: ---Request 爬虫技术,lxml 数据提取,异常护理,Fofa 等使用说明---掌握利用公开或 0day 漏洞进行批量化的收集及验证脚本开发Python 开发-某漏洞 POC 验证批量脚本---glassfish存在任意文件读取在默认4…...

Linux系统中部署软件
目录 1.Mysql 2.Redis 3.ZooKeeper 声明 致谢 1.Mysql 参考:CentOS7安装MySQL 补充: ① 执行:rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022 再执行:yum -y install mysql-community-server ② mysql…...

PHP常用框架介绍与比较
HP是一种广泛应用于Web开发的编程语言。随着互联网的快速发展,PHP的应用场景变得越来越广泛,从简单的网站到复杂的Web应用程序都可以使用PHP来开发。为了更好地组织和管理PHP代码,开发人员经常会使用框架来提高开发效率和代码质量。 本文将介绍一些常用的PHP框架,并进行简…...

Umi + React + Ant Design Pro 项目实践(一)—— 项目搭建
学习一下 Umi、 Ant Design 和 Ant Design Pro 从 0 开始创建一个简单应用。 首先,新建项目目录: 在项目目录 D:\react\demo 中,安装 Umi 脚手架: yarn create umi # npm create umi安装成功: 接下来,…...
)
MySQL知识点总结(1)
目录 1、sql、DB、DBMS分别是什么,他们之间的关系? 2、什么是表? 3、SQL语句怎么分类呢? 4、导入数据 5、什么是sql脚本呢? 6、删除数据库 7、查看表结构 8、表中的数据 10、查看创建表的语句 11、简单的查询…...
)
day45第九章动态规划(二刷)
今日任务 70.爬楼梯(进阶)322.零钱兑换279.完全平方数 70.爬楼梯(进阶) 题目链接: https://leetcode.cn/problems/climbing-stairs/description/ 题目描述: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不…...
第十四届蓝桥杯第三期模拟赛原题与详解
文章目录 一、填空题 1、1 找最小全字母十六进制数 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 给列命名 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 日期相等 1、3、1 题目描述 1、3、2 题解关键思路与解答 1、4 乘积方案数 1、4、1 题目描…...
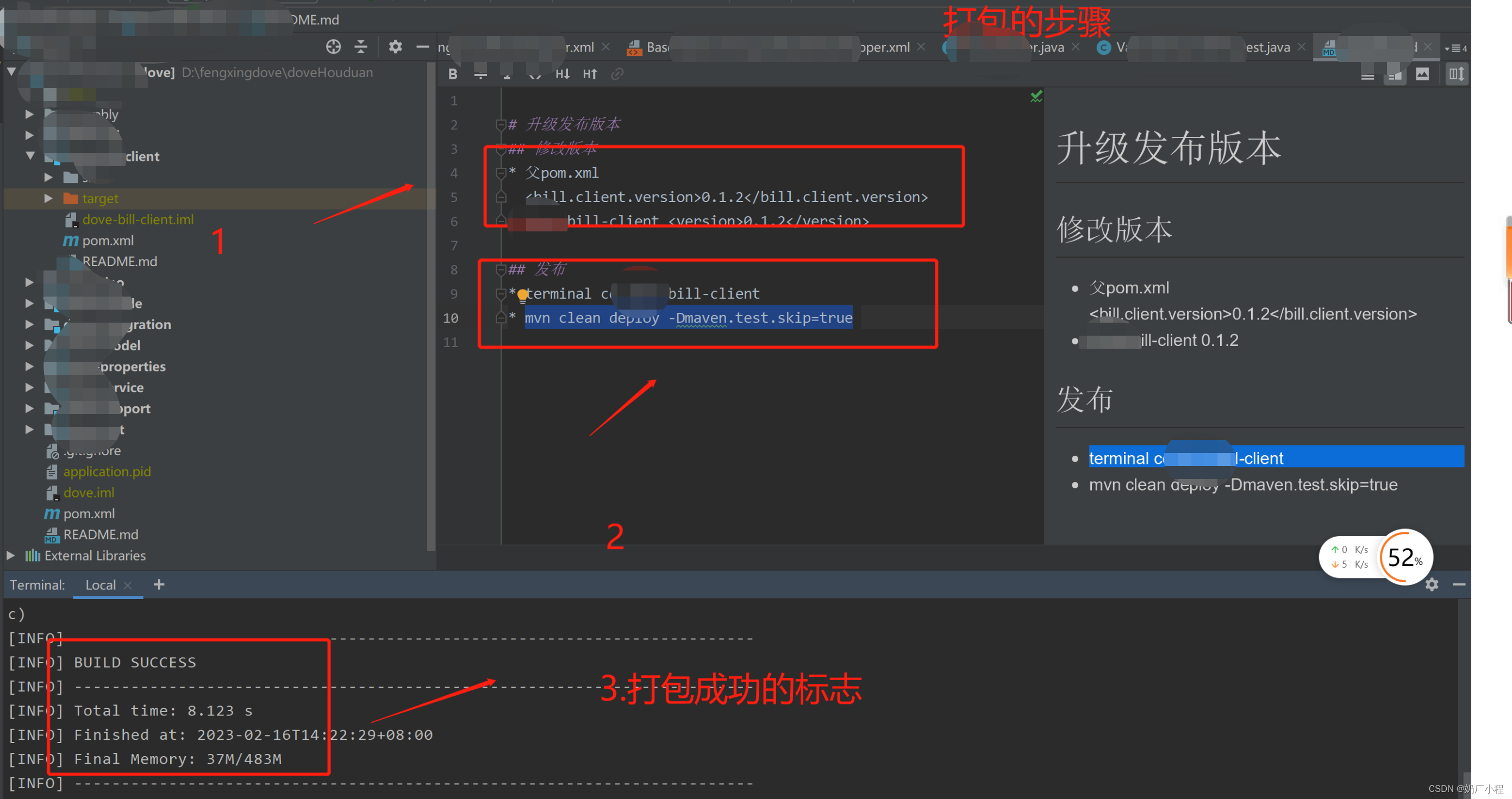
client打包升级
目录 前言 一、client如何打包升级? 二、使用步骤 1.先进行改版本 2.执行打包升级命令 总结 前言 本文章主要记录一下,日常开发中,常需要进行打包升级的步骤。 一、client如何打包升级? # 升级发布版本 ## 修改版本 * 父p…...

Blazor_WASM之3:项目结构
Blazor_WASM之3:项目结构 Blazor WebAssembly项目模板可选两种,Blazor WebAssemblyAPP及Blazor WebAssemblyAPP-Empty 如果使用Blazor WebAssemblyAPP模板,则应用将填充以下内容: 一个 FetchData 组件的演示代码,该…...

OperWrt 包管理系统02
文章目录 OperWrt 包管理系统OPKG简介OPKG的工作原理OPKG命令介绍软件包的更新、安装、卸载和升级等功能软件包的信息查询OPKG配置文件说明OPKG包结构(.ipk)OPKG演示案例OperWrt 包管理系统 OPKG简介 OPKG(Open/OpenWrt Package)是一个轻量快速的软件包管理系统,是 IPKG…...
人人都学会APP开发 提高就业竞争力 简单实用APP应用 安卓浏览器APP 企业内部通用APP制作 制造业通用APP
安卓从2009年开始流程于手机、平板,已经是不争的非常强大生产力工具,更为社会创造非常高的价值,现在已经是202X年,已经十几年的发展,安卓平台已经无所不在。因此建议人人都学学APP制作,简易入门,…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
