代码随想录第34天| 1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果
1005.K次取反后最大化的数组和
1005. K 次取反后最大化的数组和 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,这不就是常识?还能叫贪心?LeetCode:1005.K次取反后最大化的数组和_哔哩哔哩_bilibili
给你一个整数数组
nums和一个整数k,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。重复这个过程恰好
k次。可以多次选择同一个下标i。以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1 输出:5 解释:选择下标 1 ,nums 变为 [4,-2,3] 。示例 2:
输入:nums = [3,-1,0,2], k = 3 输出:6 解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2 输出:13 解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。提示:
1 <= nums.length <= 104-100 <= nums[i] <= 1001 <= k <= 104
第一次贪心:局部最优:绝对值最大的负数变成正数;全局最优:和最大
第二次贪心:局部最优:数值小的正数变成负数;全局最优:和最大
具体步骤:
1、将数组按照绝对值大小从大到小排列
2、遍历数组
3、遇到负数就将负数变为正数,同时k--
4、负数改完了k仍然不为0、
5、将数组末尾的最小的正数值反复变负数又变正数,直到k=0
class Solution {public int largestSumAfterKNegations(int[] nums, int K) {// 将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小nums = IntStream.of(nums) // 将原始数组转换为 IntStream.boxed() // 装箱,将基本数据类型转换为包装类型,以便使用 sorted 方法.sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1)) // 按绝对值大小排序.mapToInt(Integer::intValue).toArray(); // 将排序后的 IntStream 转换为 int 数组int len = nums.length; // 数组长度for (int i = 0; i < len; i++) {// 从前向后遍历,遇到负数将其变为正数,同时 K--if (nums[i] < 0 && K > 0) {nums[i] = -nums[i]; // 将负数变为正数K--; // K 减一}}// 如果 K 还大于 0,那么反复转变数值最小的元素,直到 K 用完if (K % 2 == 1) nums[len - 1] = -nums[len - 1]; // 如果 K 为奇数,将最后一个元素变为负数return Arrays.stream(nums).sum(); // 返回数组元素的和}
}134. 加油站
134. 加油站 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,得这么加油才能跑完全程!LeetCode :134.加油站_哔哩哔哩_bilibili
在一条环路上有
n个加油站,其中第i个加油站有汽油gas[i]升。你有一辆油箱容量无限的的汽车,从第
i个加油站开往第i+1个加油站需要消耗汽油cost[i]升。你从其中的一个加油站出发,开始时油箱为空。给定两个整数数组
gas和cost,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回-1。如果存在解,则 保证 它是 唯一 的。示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。示例 2:
输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。提示:
gas.length == ncost.length == n1 <= n <= 1050 <= gas[i], cost[i] <= 104
假设有以下情况:

当汽车从下标为0的位置开始走,当走到下标为3的位置时, 剩余的油不够在这里的消耗,所以没有办法走到尾部,此时从下标为4的位置重新开始走,代码如下:
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {// 初始化当前累计油量、总累计油量和起始加油站索引int curSum = 0;int totalSum = 0;int index = 0;// 遍历每个加油站for (int i = 0; i < gas.length; i++) {// 计算当前累计油量和总累计油量curSum += gas[i] - cost[i];totalSum += gas[i] - cost[i];// 如果当前累计油量为负,则说明无法从当前加油站出发,更新起始加油站索引,并将当前累计油量重置为0if (curSum < 0) {index = (i + 1);curSum = 0;}}// 如果总累计油量为负,则说明无法绕行一圈,返回-1;否则返回起始加油站索引if (totalSum < 0) return -1;return index;}
}
135. 分发糖果
135. 分发糖果 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
贪心算法,两者兼顾很容易顾此失彼!LeetCode:135.分发糖果_哔哩哔哩_bilibili
n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。- 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2] 输出:5 解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。示例 2:
输入:ratings = [1,2,2] 输出:4 解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。提示:
n == ratings.length1 <= n <= 2 * 1040 <= ratings[i] <= 2 * 104
精髓在于不要同时比较左右。
先从前向后遍历确定右边评分大于左边的情况,再从后往前遍历确定左边评分大于右边的情况。
从前向后遍历确定右边评分大于左边的情况:
局部最优:右边评分比左边大,右边的孩子就多一颗糖果;全局最优:相邻孩子中,评分高的右孩子比左孩子获得更多的糖果。
for (int i = 1; i < len; i++) {candyVec[i] = (ratings[i] > ratings[i - 1]) ? candyVec[i - 1] + 1 : 1;}此时结果如图:
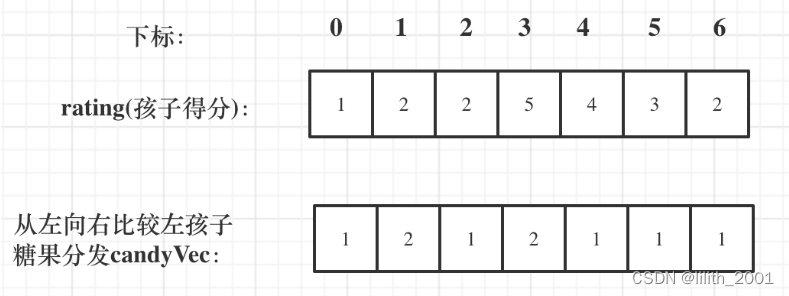
再确定左孩子大于右孩子的情况(从后向前遍历):
// 第二次遍历,从右往左分糖果,只要左边的孩子评分比右边的大,左边的孩子的糖果数应该取本身的糖果数和右边孩子糖果数 + 1 二者的最大值for (int i = len - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);}}
综合代码:
class Solution {/*** 分两个阶段* 1、起点下标1 从左往右,只要 右边 比 左边 大,右边的糖果=左边 + 1* 2、起点下标 ratings.length - 2 从右往左, 只要左边 比 右边 大,此时 左边的糖果应该 取本身的糖果数(符合比它左边大) 和 右边糖果数 + 1 二者的最大值,这样才符合 它比它左边的大,也比它右边大*/public int candy(int[] ratings) {int len = ratings.length; // 计算评分数组的长度int[] candyVec = new int[len]; // 创建一个与评分数组等长的数组,用于存储每个孩子分到的糖果数量candyVec[0] = 1; // 第一个孩子至少分到一个糖果// 第一次遍历,从左往右分糖果,只要右边的孩子评分比左边的大,右边的孩子糖果数就比左边多1for (int i = 1; i < len; i++) {candyVec[i] = (ratings[i] > ratings[i - 1]) ? candyVec[i - 1] + 1 : 1;}// 第二次遍历,从右往左分糖果,只要左边的孩子评分比右边的大,左边的孩子的糖果数应该取本身的糖果数和右边孩子糖果数 + 1 二者的最大值for (int i = len - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1]) {candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);}}// 计算总共需要的糖果数int ans = 0;for (int num : candyVec) {ans += num;}return ans; // 返回总共需要的糖果数}
}
相关文章:

代码随想录第34天| 1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果
1005.K次取反后最大化的数组和 1005. K 次取反后最大化的数组和 - 力扣(LeetCode) 代码随想录 (programmercarl.com) 贪心算法,这不就是常识?还能叫贪心?LeetCode:1005.K次取反后最大化的数组和_哔哩哔…...
Rust线程间通信通讯channel的理解和使用
Channel允许在Rust中创建一个消息传递渠道,它返回一个元组结构体,其中包含发送和接收端。发送端用于向通道发送数据,而接收端则用于从通道接收数据。不能使用可变变量的方式,线程外面修改了可变变量的值,线程里面是拿不…...
Vue3组件基础示例
组件是vue中最推崇的,也是最强大的功能之一,就是为了提高重用性,减少重复性的开发。 如何使用原生HTML方法实现组件化 在使用原生HTML开发时,我们也会遇到一些常见的功能、模块,那么如何在原生HTML中使用组件化呢&am…...
如何使用PL/SQL Developer工具导出clob字段的表?
1 准备测试数据 导出测试对象:表test_0102,others字段为clob类型 --创建中间表test_0101 create table test_0101( id number, name varchar2(20), others clob);--插入100条测试数据 beginfor i in 1..100 loopinsert into test_0101 values(i,i||_a,l…...

蓝桥杯刷题 深度优先搜索-[NewOJ P1158]N皇后(C++)
题目描述 n皇后问题:n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 上面布局用序列2 4 6 1 3 5表示,第i个数字表示第i行皇后放的列号。 按照这种格式输出前3个解,并统计总解数。 输入格式 输入一个正整数n&a…...
)
python实例2.2:编写一个装饰器,计算任何一个函数执行的时间(详解及其知识点拓展)
目录 一、编写一个装饰器,计算任何一个函数执行的时间 二、装饰器详解,及其用法举例...
Jenkins 持续集成 【CICD】
持续集成 (Continuous integration,简称CI) 持续集成是一种开发实践,它倡导团队成员频繁的集成他们的工作,每次集成都通过自动化构建(包括编译、构建、打包、部署、自动化测试)来验证ÿ…...

【CHI】(十二)Memory Tagging
目录 1. Introduction 2. Message extensions 3. Tag coherency 4. Read transaction rules 4.1 TagOp values 4.2 Permitted initial MTE tag states 5. Write transactions 5.1 Permitted TagOp values 5.2 TagOp, TU, and tags relationship 6. Dataless transact…...

Vue - 你知道Vue组件之间是如何进行数据传递的吗
难度级别:中级及以上 提问概率:85% 这道题还可以理解为Vue组件之间的数据是如何进行共享的,也可以理解为组件之间是如何通信的,很多人叫法不同,但都是说的同一个意思。我们知道,在Vue单页面应用项目中,所有的组件都是被嵌套在App.vue内…...

IP网络对讲广播系统审计
前言 这个系统是前两年在一个内网遇到的,当时顺手试了一个admin登陆之后再没有然后了,最近发现有大佬分享关于这个系统的漏洞,于是就把自己当初看的几个漏洞分享一下,系统比较简单,漏洞点很多,不要做坏事哦…...

蓝桥杯刷题--python38
197. 阶乘分解 - AcWing题库 def init(n): for i in range(2,n1): if not st[i]:primes.append(i) j0 while primes[j]*i<n: st[i*primes[j]]1 if i%primes[j]0: break j1 nint(input(…...
)
【LeetCode热题100】33. 搜索旋转排序数组(二分)
一.题目要求 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], …...
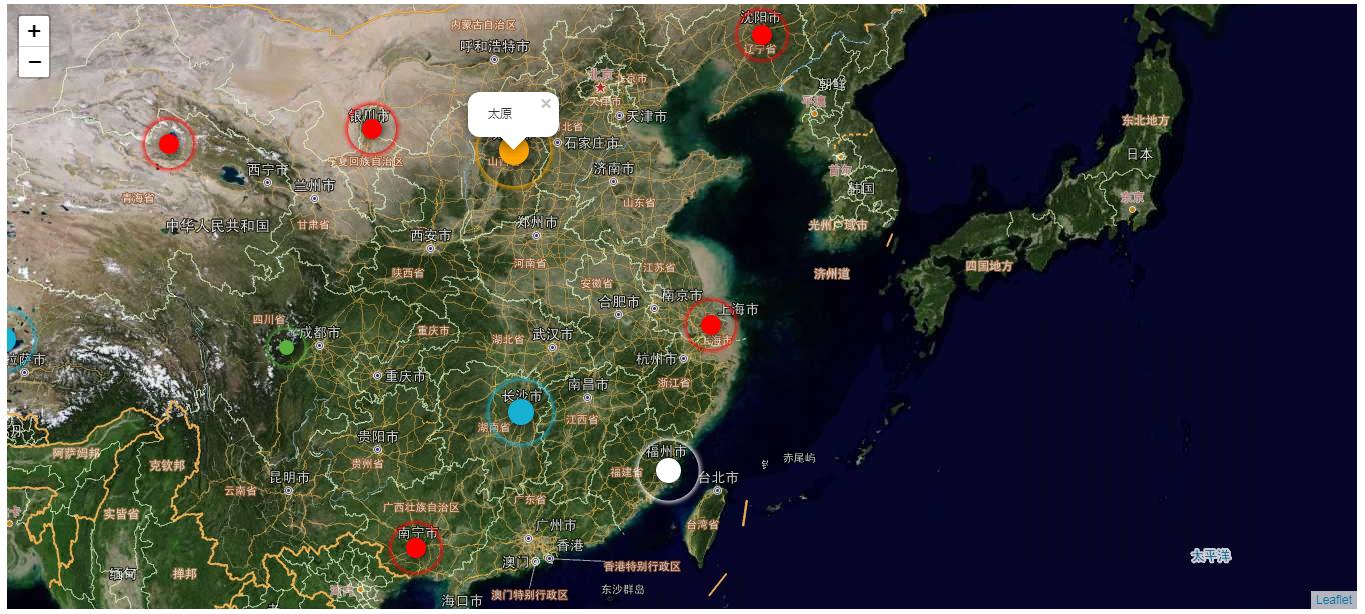
基于Leaflet.js的Marker闪烁特效的实现-模拟预警
目录 前言 一、闪烁组件 1、关于leaflet-icon-pulse 2、 使用leaflet-icon-pulse 3、方法及参数简介 二、闪烁实例开发 1、创建网页 2、Marker闪烁设置 3、实际效果 三、总结 前言 在一些地质灾害或者应急情况当中,或者热门预测当中。我们需要基于时空位置来…...
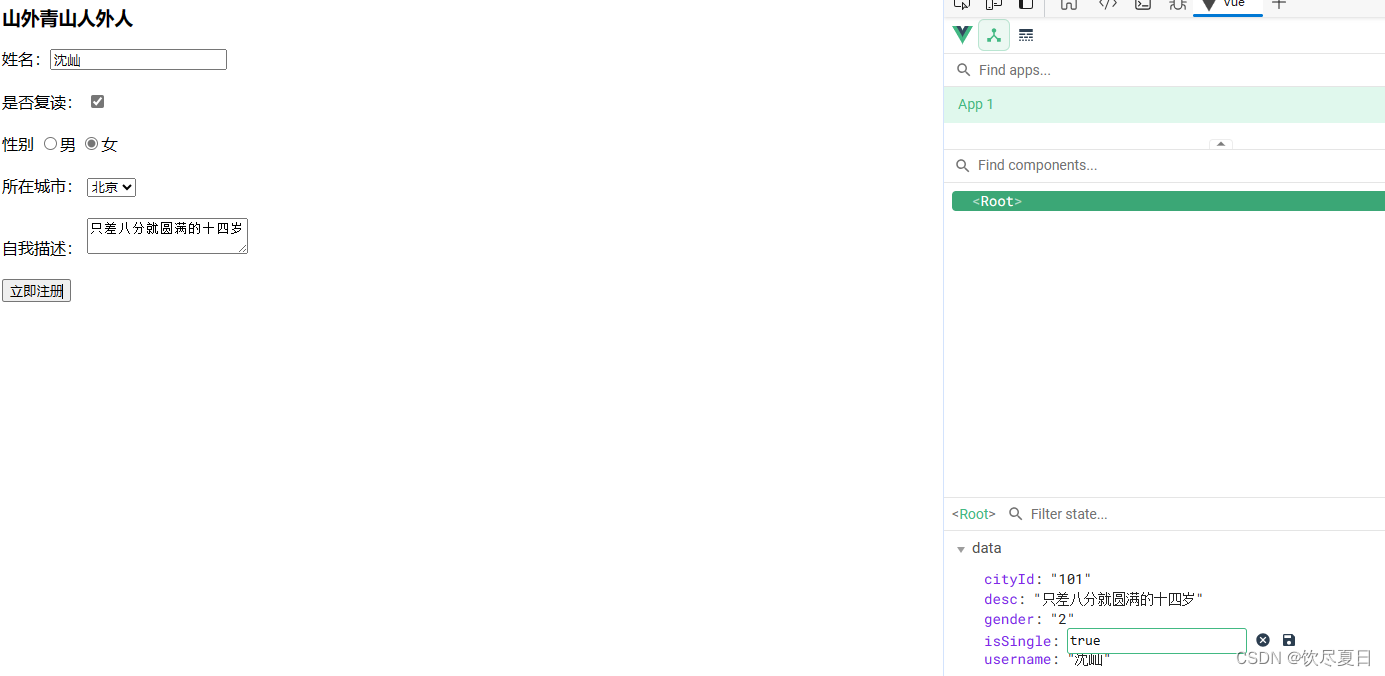
Vue-05
v-model 应用于其他表单元素 常见的表单元素都可以用v-model绑定关联 → 快速获取或设置表单元素的值 它会根据控件类型自动选取正确的方法来更新元素 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name…...

Mongodb中一个小巧的数据更新命令$inc
学习mongodb,体会mongodb的每一个使用细节,欢迎阅读威赞的文章。这是威赞发布的第55篇mongodb技术文章,欢迎浏览本专栏威赞发布的其他文章。 $inc是一个很小巧的命令。说它小巧,一个是因为短,只有三个字符。另一个是说…...
Java基于SpringBoot+Vue的专家医院预约挂号系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

STM32一个地址未对齐引起的 HardFault 异常
1. 概述 客户在使用 STM32G070 的时候,KEIL MDK 为编译工具,当编译优化选项设置为Level0 的时候,程序会出现 Hard Fault 异常,而当编译优化选项设置为 Level1 的时候,则程序运行正常。表面上看,这似乎是 K…...
spring事务那些事
实际工作中还会面临千奇百怪的问题,看下面返个例子(注意MySql数据库测试): //1.hello1Service 调用 hello2Service Transactional(propagation Propagation.REQUIRED,rollbackFor Exception.class) public void doUpdate() {//…...

设计模式深度解析:AI大模型下的策略模式与模板方法模式对比解析
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》《MYSQL应用》 💪🏻 制定明确可量化的目标,坚持默默的做事。 策略模式与模板方法模式对比解析 文章目录 🌟引言🌟Part 1:…...

贪婪算法python实现
贪婪算法(Greedy Algorithm)是一种解决问题的策略,它基于一种贪心的思想:在每一步选择中都采取当前状态下最好或最优的选择,从而希望最终能够得到全局最优解。 其核心思想可以简单概括为“当前局部最优选择”ÿ…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
