0104练习与思考题-算法基础-算法导论第三版
2.3-1 归并示意图
- 问题:使用图2-4作为模型,说明归并排序再数组 A = ( 3 , 41 , 52 , 26 , 38 , 57 , 9 , 49 ) A=(3,41,52,26,38,57,9,49) A=(3,41,52,26,38,57,9,49)上的操作。
- 图示:

tips::有不少在线算法可视化工具(软件),但是没有演示上述归并过程的,想要完成自定义的效果,需要找一个可编程的算法可视化,参考链接3。前端使用react框架,没事研究下,争取做出如上图说是归并过程的可视化效果。
2.3-2 不使用哨兵重写MERGE
重写过程MERGE,使之不使用哨兵,而是一旦数组L或者R的所有元素均被复制回A就立刻停止,然后把另外一个数组的剩余部分复制回A。
伪代码如下:
$$
$$
MERGE(A,p,q,r)
1 n1=q-r+1
2 n2=r-q
3 let L[1...n1] and R[1...n2] be new arrays
4 for i = 1 to n1
5 L[i] = A[p+i-1]
6 for j = 1 to n2
7 R[j] = A[q+j]
8 for k = p to r
9 if i > n1 or j > n2
10 break
11 if L[i] <= R[j]
12 A[k] = l[i]
13 i = i + 1
14 else A[k] = R[j]
15 j = j + 1
16 if i <= n1 and k <= r
17 while i <= n1
18 A[k] = L[i]
19 i= i + 1
20 k = k + 1
21 if j <= n2 and k <= r
22 while j <= n2
23 A[k] = R[j]
24 j = j + 1
25 k = k + 1
tips::java代码实现参考链接2
2.3-3 数学归纳法证明归并排序的运行时间
使用数学归纳法证明:当n刚好是2的幂时,以下递归式的解是 T ( n ) = n lg n T(n)=n\lg n T(n)=nlgn,
T ( n ) = { 2 若 n = 2 2 T ( n 2 ) + n , 若 n = 2 k , k > 1 T(n)=\begin{cases} 2\quad 若n=2\\ 2T(\frac{n}{2})+n,若n=2^k,k\gt1 \end{cases} T(n)={2若n=22T(2n)+n,若n=2k,k>1
证明: 当 n = 2 1 时, T ( n ) = 2 lg 2 = 2 假设当 n = 2 k 时, T ( n ) = n lg n = k 2 K 成立 当 n = 2 k + 1 时 , T ( n ) = 2 T ( 2 k ) + 2 k + 1 = 2 k 2 k + 2 k + 1 = 2 k + 1 ( k + 1 ) = n lg n ∴ 当 n 是 2 的幂时, T ( n ) = n lg n 是上述递归式的解。 证明:\\ 当n=2^1时,T(n)=2\lg 2=2\\ 假设当n=2^k时,T(n)=n\lg n =k2^K 成立\\ 当n=2^{k+1}时,\\ T(n)=2T(2^k)+2^{k+1}=2k2^k+2^{k+1}\\ =2^{k+1}(k+1)=n\lg n\\ \therefore 当n是2的幂时,T(n)=n\lg n是上述递归式的解。 证明:当n=21时,T(n)=2lg2=2假设当n=2k时,T(n)=nlgn=k2K成立当n=2k+1时,T(n)=2T(2k)+2k+1=2k2k+2k+1=2k+1(k+1)=nlgn∴当n是2的幂时,T(n)=nlgn是上述递归式的解。
2.3-4 插入排序的递归版本
我们可以把插入排序表示为如下的一个递归过程。为例排序 A [ 1 ⋯ n ] A[1\cdots n] A[1⋯n],我们递归地排序 A [ 1 ⋯ n − 1 ] , A[1\cdots n-1], A[1⋯n−1],然后把 A [ n ] A[n] A[n]插入已排序的数组 A [ 1 ⋯ n − 1 ] A[1\cdots n-1] A[1⋯n−1]。为了插入排序的这个递归版本的最坏情况运行时间写一个递归式。
插入排序递归版本最坏情况就是数据排列顺序和需求的排序相反。把 A [ n ] A[n] A[n]插入已排序的数组 A [ 1 ⋯ n − 1 ] A[1\cdots n-1] A[1⋯n−1]运行时间为O(n),终止条件是n=1,此时数组以有序,运行时间为O(1),递归式如下:
T ( n ) = { O ( 1 ) , n = 1 T ( n − 1 ) + O ( n ) , n > 1 T(n)=\begin{cases} O(1),n=1\\ T(n-1)+O(n),n\gt 1 \end{cases} T(n)={O(1),n=1T(n−1)+O(n),n>1
T(n)的最坏情况下的运行时间为O(n^2),性能不高,这里不做实现。
2.3-5 二分查找算法运行时间
回顾查找问题(参见练习2.1-3),注意到,如果序列A已排好序,就可以将排序列中点与v进行比较。根据比较的结果,原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程,每次都讲序列剩余部分规模减半。为二分查找算法写出迭代或递归的伪代码。证明:二分查找的最坏情况运行时间为 O ( lg n ) O(\lg n) O(lgn)
分析:首先序列已排序,二分查找的最坏情况就是要查找的数不在序列中。计算序列中点,与目标值比较,如果小于大于目标值,继续在左半边序列查找;否则在右半边序列查找。直至序列长度为2,中点必为其中一个此时序列中该元素依然不等于目标值,终止。
循环递归式如下:
T ( n ) = { O ( 1 ) , n = 1 T ( n 2 ) + O ( 1 ) , n > 1 T(n)=\begin{cases} O(1),n=1\\ T(\frac{n}{2})+O(1),n\gt 1 \end{cases} T(n)={O(1),n=1T(2n)+O(1),n>1
二分查找运行时间 T ( n ) = lg n T(n)=\lg n T(n)=lgn,实现相对比较简单,自行搜索,这里不在详述。非递归实现参考下面链接5或者去下面列出的仓库地址中查找。
2.3-6 二分查找能改进插入排序吗?
注意到2.1节中的过程INSERTION_SORT的第5~7行的while循环采用一种线性查询来(反向)扫描已排好序的子数组 A [ 1 ⋯ j − 1 ] A[1\cdots j-1] A[1⋯j−1].我们可以使用二分查找(参见练习2.3-5)来把插入排序的最坏情况运行时间改进到 O ( n lg n ) O(n\lg n) O(nlgn)吗?
**解答:**不能。因为在第5~7步,包含查找和移动元素,查找A[j]合适位置使用二分查找运行时间为 O ( lg j ) O(\lg j) O(lgj),把该元素之后全部向后移动一位运行时间为 O ( j ) O(j) O(j),所以运行时间为 O ( j ) O(j) O(j),那么总的运行时间还是 O ( n 2 ) O(n^2) O(n2)
二、思考题
2-1 在归并排序中对小数组采用插入排序
虽然归并排序的最坏情况运行时间是 O ( n lg n ) O(n\lg n) O(nlgn),而插入排序的最坏情况运行时间是 O ( n 2 ) O(n^2) O(n2),但是插入插入排序中的常量因子可能使得它在n较小时,在许多机器上实际运行的更快。因此,在归并排序中当子问题变得足够小时,采用插入排序来使递归的叶变粗是有意义的。考虑对归并排序的一种修改,其中使用插入排序来排序长度为k的 n k \frac{n}{k} kn个子表,然后使用标准的合并机制来合并这些子表,这里k是一个待定的值。
a. 证明插入排序最坏情况下可以在 O ( n k ) O(nk) O(nk)时间内排序每个长度为k的 n k \frac{n}{k} kn歌子表。
b. 表名在最坏情况下如何在 O [ n lg ( n k ) ] O[n\lg(\frac{n}{k})] O[nlg(kn)]时间内合并这些子表。
c. 假定修改后的算法的最坏情况运行时间为 O [ n k + n lg ( n k ) ] O[nk+n\lg(\frac{n}{k})] O[nk+nlg(kn)],要使修改后的算法与标准的归并排序具有相同的运行时间,作为n的一个函数,记住O记号,k的最大值是什么?
d. 在实践中,我们应该如何选择k?
a . 插入排序长度为 k 的在最坏情况下运行时间为 O ( k 2 ) ∴ n k 个子表花费时间为 O ( k 2 ⋅ n k ) = O ( n k ) b . 合并长度为 k 的 n k 的子表,每次合并 2 个子表 需要合并的层数为 lg ( n k ) + 1 , 每层需要比较 n 次 ∴ 最坏情况下运行时间为 n lg ( n k ) c . 修改后的算法与标准的归并排序有想听的运行时间,即 O ( n k + n lg ( n k ) ) = O ( n lg n ) 令 k = O ( lg n ) , 有 O ( n k + n lg ( n k ) ) = O ( n k + n lg n − n lg k ) = O ( 2 n lg n − n lg lg n ) = O ( n lg n ) d . 实践中, k 取插入排序比归并排序的最大值。 a. 插入排序长度为k的在最坏情况下运行时间为O(k^2)\\ \therefore \frac{n}{k}个子表 花费时间为O(k^2\cdot \frac{n}{k})=O(nk)\\ b. 合并长度为k的\frac{n}{k}的子表,每次合并2个子表\\ 需要合并的层数为\lg(\frac{n}{k})+1,每层需要比较n次\\ \therefore 最坏情况下运行时间为n\lg(\frac{n}{k})\\ c. 修改后的算法与标准的归并排序有想听的运行时间,即\\ O(nk+n\lg(\frac{n}{k}))=O(n\lg n)\\ 令k=O(\lg n),有\\ O(nk+n\lg(\frac{n}{k}))=O(nk+n\lg n-n\lg k)\\ =O(2n\lg n-n\lg\lg n) =O(n\lg n)\\ d.实践中,k取插入排序比归并排序的最大值。 a.插入排序长度为k的在最坏情况下运行时间为O(k2)∴kn个子表花费时间为O(k2⋅kn)=O(nk)b.合并长度为k的kn的子表,每次合并2个子表需要合并的层数为lg(kn)+1,每层需要比较n次∴最坏情况下运行时间为nlg(kn)c.修改后的算法与标准的归并排序有想听的运行时间,即O(nk+nlg(kn))=O(nlgn)令k=O(lgn),有O(nk+nlg(kn))=O(nk+nlgn−nlgk)=O(2nlgn−nlglgn)=O(nlgn)d.实践中,k取插入排序比归并排序的最大值。
Java算法实现参考edu.princeton.cs.algs4.MergeX
2-2 冒泡排序的正确性
冒泡排序是一种流行但低效的排序算法,它的作用是反复交换相邻的未按次序排序的元素。
BUBBLESORT(A)
1 for i = 1 to A.length -1
2 for j = A.length downto i+1
3 if A[j]< A[j-1]
4 exchange A[j] wiht A[j-1]
a. 假设 A ′ A^{'} A′表示BUBBLESORT(A)的输出。为了证明BUBBLESORT正确,我们必须证明它将终止并且有:
A ′ [ 1 ] ≤ A ′ [ 2 ] ≤ ⋯ ≤ A ′ [ n ] A^{'}[1]\le A^{'}[2]\le \cdots\le A^{'}[n] A′[1]≤A′[2]≤⋯≤A′[n]
其中 n = A . l e n g t h n=A.length n=A.length。为了证明BUBBLESORT确实完成了排序,我们还需要证明什么?下面两部分讲证明上述不等式。
b. 为第2~4行的for循环精确地说明一个循环不变式,并证明该循环不变式成立。你的证明应该使用本章中给出的循环不变式证明的结果。
c. 使用(b)部分证明的循环不变式的终止条件,为第1~4行的for循环说明一个循环不变式,该不变式将使你证明不等式。你的证明应该使用本章中给出的循环不变式证明的结构。
d. 冒泡排序的最坏情况下运行时间是多少?与插入排序的运行时间相比,其性能如何?
$$
a.\ 我们需要证明A^{'}的元素都来自A且以排序。\
b. \
循环不变式: 2~4行迭代开始,A[j\cdots n]元素为原A[j\cdots n]的元素,可能顺序不同\
且A[j]为其中最小的元素.\
初始:初始子数组元素只有A[n],为当前数组最小元素。\
维持:每次迭代,我们比较A[j]与A[j-1]的大小,确保A[j-1]为其中的最小值。迭代完成后,子数组元素加1,且第一个元素为其中最小值。\
终止:终止条件为j=i。此时A[i]是子数组A[i\cdots n]中最小元素,其中A[i\cdots n]元素是原数组中A[i\cdots n]。\
c.\
循环不变式:1-4行循环起始,子数组A[1\cdots i -1]为A[1\cdots n]中最小的i-1个元素,且以排序;A[i\cdots n]为A[1\cdots n]中剩余n-i+1个元素。\
初始:子数组A[1\cdots i-1]为空。\
维持:根据(b)有,执行完内循环之后,A[i]为子数组A[i\cdots n]中的最小值。在外循环的起始A[1\cdots i-1]元素比A[i\cdots n]中元素小且以排序。\那么每次外循环执行完成后A[1\cdots i]为比数组A[i+1\cdots n]中的元素小且以排序。\
终止:当i=n.length 时,循环终止。此时A[1\cdots n]以全部完成排序。\
d.\
冒泡排序在最坏情况下运行时间为O(n^2),和插入排序一样。
$$
2-3 霍纳规则的正确性
给定系数 a 0 , a 1 , ⋯ , a n 和 x a_0,a_1,\cdots,a_n和x a0,a1,⋯,an和x的值,代码片段
1 y=0
2 for in downto 0
3 y = a_i+xy
实现了用于求值多项式
P ( x ) = ∑ k = 0 n a k x k = a 0 + x ( a 1 + x ( a 2 + ⋯ + x ( a n − 1 + x a n ) ⋯ ) ) P(x)=\sum_{k=0}^na_kx^k=a_0+x(a_1+x(a_2+\cdots +x(a_n-1 + xa_n)\cdots)) P(x)=k=0∑nakxk=a0+x(a1+x(a2+⋯+x(an−1+xan)⋯))
的霍纳规则。
a. 借助O记号,实现霍纳规则的以上代码片段的运行时间是多少?
b. 编写伪代码来实现朴素的多项式求值算法,该算法从头开始计算多项式的每个项。该算法的运行时间是多少?与霍纳规则相比,其性能如果?
c. 考虑以下循环不变式:
在第2~3for循环每次迭代的开始有
y = ∑ k = 0 n − ( i + 1 ) a k + i + 1 x k y=\sum_{k=0}^{n-(i+1)}a_{k+i+1}x^k y=k=0∑n−(i+1)ak+i+1xk
把没有项的合式解释为等于0.遵照本章中给出的循环不变式证明的结构,使用该循环不变式来证明终止时有 P ( x ) = ∑ k = 0 n a k x k P(x)=\sum_{k=0}^na_kx^k P(x)=∑k=0nakxk
d. 最后证明上面给出的代码片段将正确地求由系数 a 0 , a 1 , ⋯ , a n a_0,a_1,\cdots,a_n a0,a1,⋯,an刻画的多项式的值。
a 运行时间为 O ( n ) a\\ 运行时间为O(n)\\ a运行时间为O(n)
b. \\
NAIVE-HORNER()y = 0for k = 0 to ntemp = 1for i = 1 to ktemp = temp * xy = y + a[k] * temp运行时间为 O ( n 2 ) O(n^2) O(n2),比霍纳规则慢。
c . 初始: y = 0 维持: y = a i + x ∑ k = 0 n − ( i + 1 ) a k + i + 1 x k = a i x 0 + ∑ k = 0 n − ( i + 1 ) a k + i + 1 x k + 1 = a i x 0 + ∑ k = 0 n − i a k + i x k = ∑ k = 0 n − i a k + i x k 终止:此时 i = − 1 y = ∑ k = 0 n a k x k d . 循环的不变量是与给定系数的多项式相等的和。 c. \\ 初始:y=0\\ 维持:y=a_i+x\sum_{k=0}^{n-(i+1)}a_{k+i+1}x^k\\ =a_ix^0+\sum_{k=0}^{n-(i+1)}a_{k+i+1}x^{k+1}\\ =a_ix^0+\sum_{k=0}^{n-i}a_{k+i}x^k\\ =\sum_{k=0}^{n-i}a_{k+i}x^k\\ 终止:此时i=-1\\ y=\sum_{k=0}^na_kx^k\\ d. \\ 循环的不变量是与给定系数的多项式相等的和。 c.初始:y=0维持:y=ai+xk=0∑n−(i+1)ak+i+1xk=aix0+k=0∑n−(i+1)ak+i+1xk+1=aix0+k=0∑n−iak+ixk=k=0∑n−iak+ixk终止:此时i=−1y=k=0∑nakxkd.循环的不变量是与给定系数的多项式相等的和。
2-4 逆序对
假设 A [ 1 ⋯ n ] A[1\cdots n] A[1⋯n]是一个有n个不同数的数组。若 i < j 且 A [ i ] > A [ j ] i\lt j且A[i]\gt A[j] i<j且A[i]>A[j],则对偶 ( i , j ) (i,j) (i,j)称为A的一个逆序对(inversion)。
a. 列出数组(2,3,8,6,1)的5个逆序对。
b. 由集合 [ 1 , 2 , ⋯ , n ] [1,2,\cdots,n] [1,2,⋯,n]中的元素构成的什么数组具有最多的逆序对?它有多少逆序对?
c. 插入排序的运行时间与输入数组中逆序对的数量之间是什么关系?证明你的回答。
d. 给出一个确定在n个元素的任何排列中逆序对数量的算法,最坏情况下需要 O ( n k + n lg ( n k ) ) O(nk+ n\lg(\frac{n}{k}) ) O(nk+nlg(kn))的时间。(提示:修改归并排序)
a . ( 2 , 1 ) , ( 3 , 1 ) , ( 8 , 6 ) , ( 8 , 1 ) , ( 6 , 1 ) b . 数组 [ n , n − 1 , ⋯ , 1 ] 具有对多的逆序对,逆序对数为 ( n − 1 ) n 2 c . 插入排序的运行时间是逆序对数的常量倍数。 d a. \\ (2,1),(3,1),(8,6),(8,1),(6,1)\\ b. \\ 数组[n,n-1,\cdots,1]具有对多的逆序对,逆序对数为\frac{(n-1)n}{2}\\ c. \\ 插入排序的运行时间是逆序对数的常量倍数。\\ d a.(2,1),(3,1),(8,6),(8,1),(6,1)b.数组[n,n−1,⋯,1]具有对多的逆序对,逆序对数为2(n−1)nc.插入排序的运行时间是逆序对数的常量倍数。d
结合2-1,Java代码实现如下所示:
package com.gaogzhen.introductiontoalgorithms3.foundation;import edu.princeton.cs.algs4.MergeX;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;import java.util.Comparator;/*** 求解逆序对的数量* 1 逆序:对于n个不同的元素,先规定各演示之间有一个标准次序(例如n个不同的自然数,可规定由小到大为标准次序),与是在这n个元素的任一排序中,当某一对元素的先后次序与标准次序不同时,* 就说它构成1个逆序。* 2 逆序数:一个排列中所有逆序的总数叫做这个排列的逆序数。* 逆序对数=交换次数** @author gaogzhen* @since 2024/4/7 21:46*/
public class Inversion {private static final int CUTOFF = 7; // cutoff to insertion sort// This class should not be instantiated.private Inversion() { }/*** 归并统计交换次数* @param src 源子数组* @param dst 目的子数组* @param lo 起始索引* @param mid 中间索引* @param hi 结束索引* @return*/private static int merge(Comparable[] src, Comparable[] dst, int lo, int mid, int hi) {// precondition: src[lo .. mid] and src[mid+1 .. hi] are sorted subarrays// assert isSorted(src, lo, mid);// assert isSorted(src, mid+1, hi);int i = lo, j = mid+1;// 交换次数int inversions = 0;for (int k = lo; k <= hi; k++) {if (i > mid) {// 低位归并完成需要计数dst[k] = src[j++];} else if (j > hi) {// 高位归并完成,不需要计数dst[k] = src[i++];} else if (less(src[j], src[i])) {// 交换次数=mid - lo + 1 - i + 1inversions += mid - lo + 1 - i + 1;dst[k] = src[j++]; // to ensure stability} else {// 归并低位需要计数dst[k] = src[i++];}}// postcondition: dst[lo .. hi] is sorted subarray// assert isSorted(dst, lo, hi);return inversions;}/*** 统计逆序对数* @param src 源子数组* @param dst 目的(交换)子数组* @param lo 低位起始索引* @param hi 高位终止索引* @return*/private static int sort(Comparable[] src, Comparable[] dst, int lo, int hi) {// if (hi <= lo) return;if (hi <= lo + CUTOFF) {// 小数组使用插入排序统计逆序对数return insertionSort(dst, lo, hi);}int mid = lo + (hi - lo) / 2;// 统计左子树组逆序对数int left = sort(dst, src, lo, mid);// 统计左子树组逆序对数int right = sort(dst, src, mid+1, hi);// if (!less(src[mid+1], src[mid])) {// for (int i = lo; i <= hi; i++) dst[i] = src[i];// return;// }// using System.arraycopy() is a bit faster than the above loopif (!less(src[mid+1], src[mid])) {// 左子树组和右子树组完成排序好,且左侧最大元素小于右侧最小元素,无需交换System.arraycopy(src, lo, dst, lo, hi - lo + 1);return left + right;}// 统计归并左右子数组逆序对数int inversions = merge(src, dst, lo, mid, hi);return inversions + left + right;}/*** 统计数组a的逆序对数* @param a 目标数组*/public static int sort(Comparable[] a) {Comparable[] aux = a.clone();int inversions = sort(aux, a, 0, a.length-1);// assert isSorted(a);return inversions;}/*** 插入排序统计逆序对数* @param a 目标数组* @param lo 低位起始索引* @param hi 高位终止索引* @return*/private static int insertionSort(Comparable[] a, int lo, int hi) {int inversions = 0;for (int i = lo; i <= hi; i++) {for (int j = i; j > lo && less(a[j], a[j-1]); j--) {exch(a, j, j-1);// 交换一次,逆序数+1inversions++;}}return inversions;}/******************************************************************** Utility methods.*******************************************************************//*** 交换元素* @param a 目标数组* @param i 交换元素索引* @param j 另一个交换式索引*/private static void exch(Object[] a, int i, int j) {Object swap = a[i];a[i] = a[j];a[j] = swap;}/*** 第一个元素是否小于第二个元素* @param a 第一个元素* @param b 第二个元素* @return {@true} a 小于b ;else {@false}*/private static boolean less(Comparable a, Comparable b) {return a.compareTo(b) < 0;}/*** 使用比较器,比较a是否小于b* @param a 元素a* @param b 元素吧* @param comparator 比较器* @return*/private static boolean less(Object a, Object b, Comparator comparator) {return comparator.compare(a, b) < 0;}/******************************************************************** Version that takes Comparator as argument.*******************************************************************//*** Rearranges the array in ascending order, using the provided order.** @param a the array to be sorted* @param comparator the comparator that defines the total order*/public static void sort(Object[] a, Comparator comparator) {Object[] aux = a.clone();sort(aux, a, 0, a.length-1, comparator);// assert isSorted(a, comparator);}private static void merge(Object[] src, Object[] dst, int lo, int mid, int hi, Comparator comparator) {// precondition: src[lo .. mid] and src[mid+1 .. hi] are sorted subarrays// assert isSorted(src, lo, mid, comparator);// assert isSorted(src, mid+1, hi, comparator);int i = lo, j = mid+1;for (int k = lo; k <= hi; k++) {if (i > mid) dst[k] = src[j++];else if (j > hi) dst[k] = src[i++];else if (less(src[j], src[i], comparator)) dst[k] = src[j++];else dst[k] = src[i++];}// postcondition: dst[lo .. hi] is sorted subarray// assert isSorted(dst, lo, hi, comparator);}private static void sort(Object[] src, Object[] dst, int lo, int hi, Comparator comparator) {// if (hi <= lo) return;if (hi <= lo + CUTOFF) {insertionSort(dst, lo, hi, comparator);return;}int mid = lo + (hi - lo) / 2;sort(dst, src, lo, mid, comparator);sort(dst, src, mid+1, hi, comparator);// using System.arraycopy() is a bit faster than the above loopif (!less(src[mid+1], src[mid], comparator)) {System.arraycopy(src, lo, dst, lo, hi - lo + 1);return;}merge(src, dst, lo, mid, hi, comparator);}// sort from a[lo] to a[hi] using insertion sortprivate static int insertionSort(Object[] a, int lo, int hi, Comparator comparator) {int inversions = 0;for (int i = lo; i <= hi; i++) {for (int j = i; j > lo && less(a[j], a[j-1], comparator); j--) {exch(a, j, j-1);inversions++;}}return inversions;}/**************************************************************************** Check if array is sorted - useful for debugging.***************************************************************************/private static boolean isSorted(Comparable[] a) {return isSorted(a, 0, a.length - 1);}private static boolean isSorted(Comparable[] a, int lo, int hi) {for (int i = lo + 1; i <= hi; i++) {if (less(a[i], a[i-1])) {return false;}}return true;}private static boolean isSorted(Object[] a, Comparator comparator) {return isSorted(a, 0, a.length - 1, comparator);}private static boolean isSorted(Object[] a, int lo, int hi, Comparator comparator) {for (int i = lo + 1; i <= hi; i++) {if (less(a[i], a[i-1], comparator)) {return false;}}return true;}/*** 输出a数组* @param a 数组*/private static void show(Object[] a) {for (int i = 0; i < a.length; i++) {StdOut.println(a[i]);}}/*** 测试*/public static void main(String[] args) {String[] a = StdIn.readAllStrings();int inversions = Inversion.sort(a);show(a);StdOut.print("逆序对数:" + inversions);}
}结语
欢迎小伙伴一起学习交流,需要啥工具或者有啥问题随时联系我。
❓QQ:806797785
⭐️源代码地址:https://gitee.com/gaogzhen/algorithm
[1]算法导论(原书第三版)/(美)科尔曼(Cormen, T.H.)等著;殷建平等译 [M].北京:机械工业出版社,2013.1(2021.1重印).p22-24
[2]归并排序-排序-算法第四版[CP/OL]
[3]CLRS Solutions[CP/OL]
[4]Algorithm Visualizer[CP/OL]
[4]入门-基础-算法第4版[CP/OL]
相关文章:

0104练习与思考题-算法基础-算法导论第三版
2.3-1 归并示意图 问题:使用图2-4作为模型,说明归并排序再数组 A ( 3 , 41 , 52 , 26 , 38 , 57 , 9 , 49 ) A(3,41,52,26,38,57,9,49) A(3,41,52,26,38,57,9,49)上的操作。图示: tips::有不少在线算法可视化工具(软…...
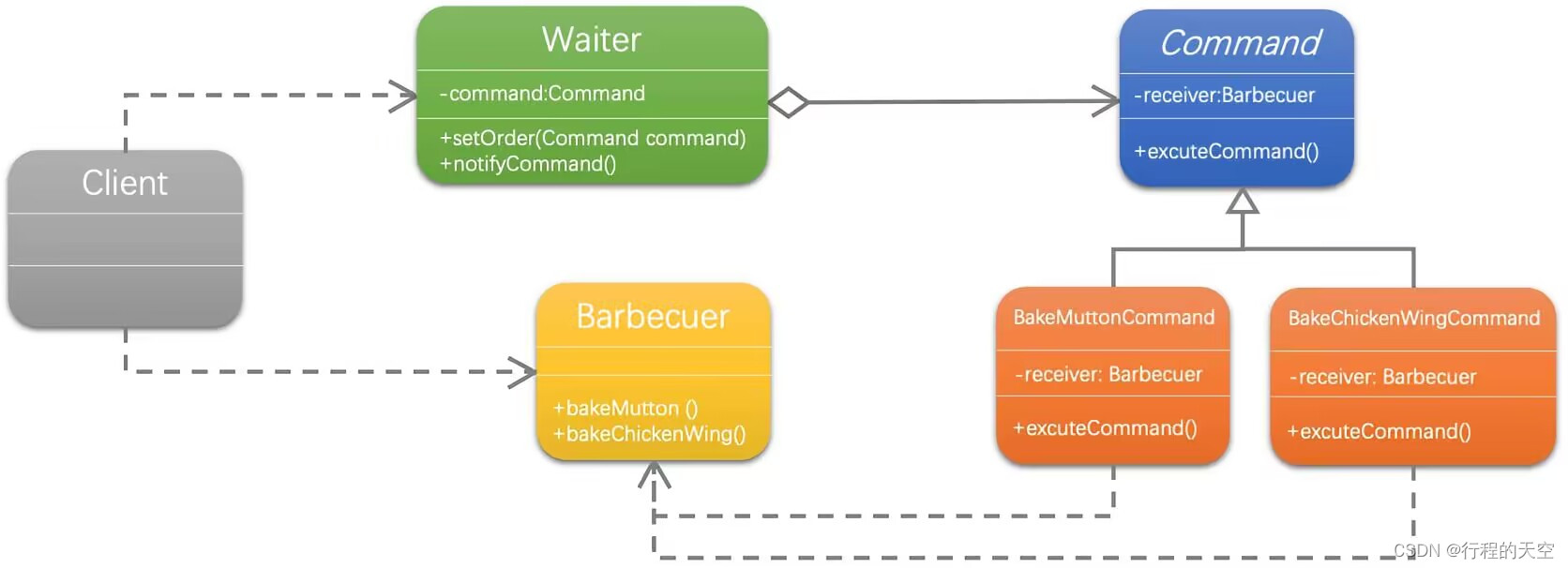
烤羊肉串引来的思考--命令模式
1.1 吃羊肉串! 烧烤摊旁边等着拿肉串的人七嘴八舌地叫开了。场面有些混乱,由于人实在太多,烤羊肉串的老板已经分不清谁是谁,造成分发错误,收钱错误,烤肉质量不过关等。 外面打游击烤羊肉串和这种开门店做烤…...

Python 描述符
文章目录 类型:数据描述符:方法描述符:描述符的要包括以下几点:方法描述符实现缓存 描述符(Descriptor)是 Python 中一个非常强大的特性,它允许我们自定义属性的访问行为。使用描述符,我们可以创建一些特殊的属性,在访问这些属性时执行自定义…...

Go语言创建HTTP服务器
Web服务器可提供网页、Web服务和文件,而Go语言为创建Web服务器提供了强大的支持。 1.通过Hello World Web 服务器宣告您的存在 标准库中的net/http包提供了多种创建HTTP服务器的方法,它还提供了一个基本的路由器。 package mainimport ("net/http" )func helloWo…...

【LeetCode热题100】【栈】柱状图中最大的矩形
题目链接:84. 柱状图中最大的矩形 - 力扣(LeetCode) 要找最大的矩形就是要找以每根柱子为高度往两边延申的边界,要作为柱子的边界就必须高度不能低于该柱子,否则矩形无法同高,也就是需要找出以每根柱子为高…...
谷歌浏览器插件开发速成指南:弹窗
诸神缄默不语-个人CSDN博文目录 本文介绍谷歌浏览器插件开发的入门教程,阅读完本文后应该就能开发一个简单的“hello world”插件,效果是出现写有“Hello Extensions”的弹窗。 作为系列文章的第一篇,本文还希望读者阅读后能够简要了解在此基…...

Lakehouse 大数据概念
“Lakehouse” 是一个相对新的概念,是大数据理论中的一个重要发展方向。它试图结合传统的数据湖(Data Lake)和数据仓库(Data Warehouse)的优点,以创造一种更为灵活和强大的数据管理体系。 在传统的大数据架构中,数据湖用于存储原始、未加工的数据,而数据仓库则用于存储…...
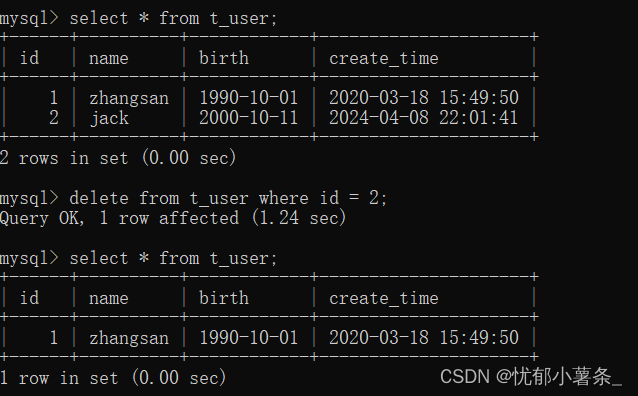
MySQL学习笔记(二)
1、把查询结果中去除重复记录 2、连接查询 从一张表中单独查询,称为单表查询。emp表和dept表联合起来查询数据,从emp表中取员工名字,从dept表中取部门名字,这种跨表查询,多张表联合起来查询数据,被称为连…...

Verilog语法——按位取反“~“和位宽扩展的优先级
前言 先说结论,如下图所示,在Verilog中“~ ”按位取反的优先级是最高的,但是在等式计算时,有时候会遇到位宽扩展,此时需要注意的是位宽扩展的优先级高于“~”。 验证 仿真代码,下面代码验证的是“~”按位取…...
Navicat工具使用
Navicat的本质: 在创立连接时提前拥有了数据库用户名和密码 双击数据库时,相当于建立了一个链接关系 点击运行时,远程执行命令,就像在xshell上操作Linux服务器一样,将图像化操作转换成SQL语句去后台执行 一、打开Navi…...
——mv、rm、which、find)
linux常用指令(一)——mv、rm、which、find
mv命令: 用于查看文件内容 语法:mv 参数1 参数2 参数1,linux路径,表示被移动的文件或文件夹 参数2,linux路径,表示要移动去的地方,如果目标不存在,则进行改名 rm命令:…...
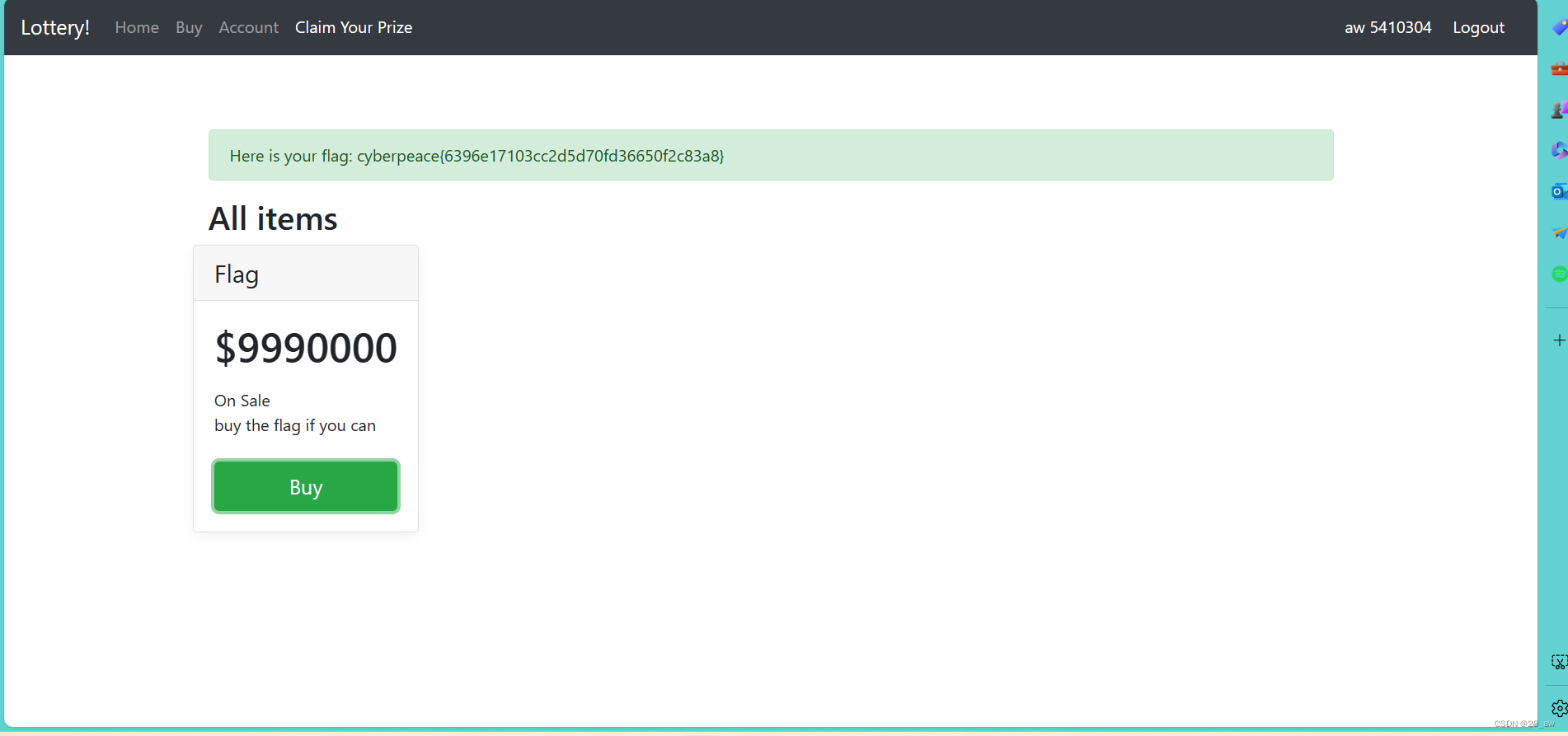
lottery-攻防世界
题目 flag在这里要用钱买,这是个赌博网站。注册个账号,然后输入七位数字,中奖会得到相应奖励。 githacker获取网站源码 ,但是找到了flag文件但是没用。 bp 抓包发现api.php,并且出现我们的输入数字。 根据题目给的附…...

深入理解指针2:数组名理解、一维数组传参本质、二级指针、指针数组和数组指针、函数中指针变量
目录 1、数组名理解 2、一维数组传参本质 3、二级指针 4、指针数组和数组指针 5、函数指针变量 1、数组名理解 首先来看一段代码: int main() {int arr[10] { 1,2,3,4,5,6,7,8,9,10 };printf("%d\n", sizeof(arr));return 0; } 输出的结果是&…...

【C/C++】C语言实现单链表
C语言实现单链表 简单描述代码运行结果 简单描述 用codeblocks编译通过 源码参考连接 https://gitee.com/IUuaena/data-structures-c.git 代码 common.h #ifndef COMMON_H_INCLUDED #define COMMON_H_INCLUDED#define ELEM_TYPE int //!< 链表元素类型/*! brief 返回值类…...
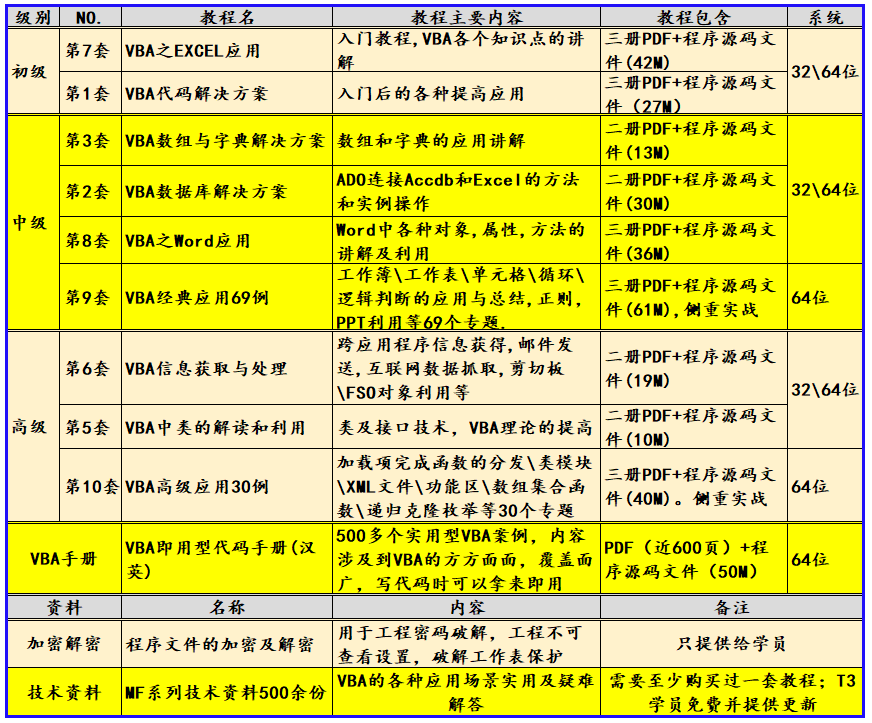
VBA数据库解决方案第九讲:把数据库的内容在工作表中显示
《VBA数据库解决方案》教程(版权10090845)是我推出的第二套教程,目前已经是第二版修订了。这套教程定位于中级,是学完字典后的另一个专题讲解。数据库是数据处理的利器,教程中详细介绍了利用ADO连接ACCDB和EXCEL的方法…...
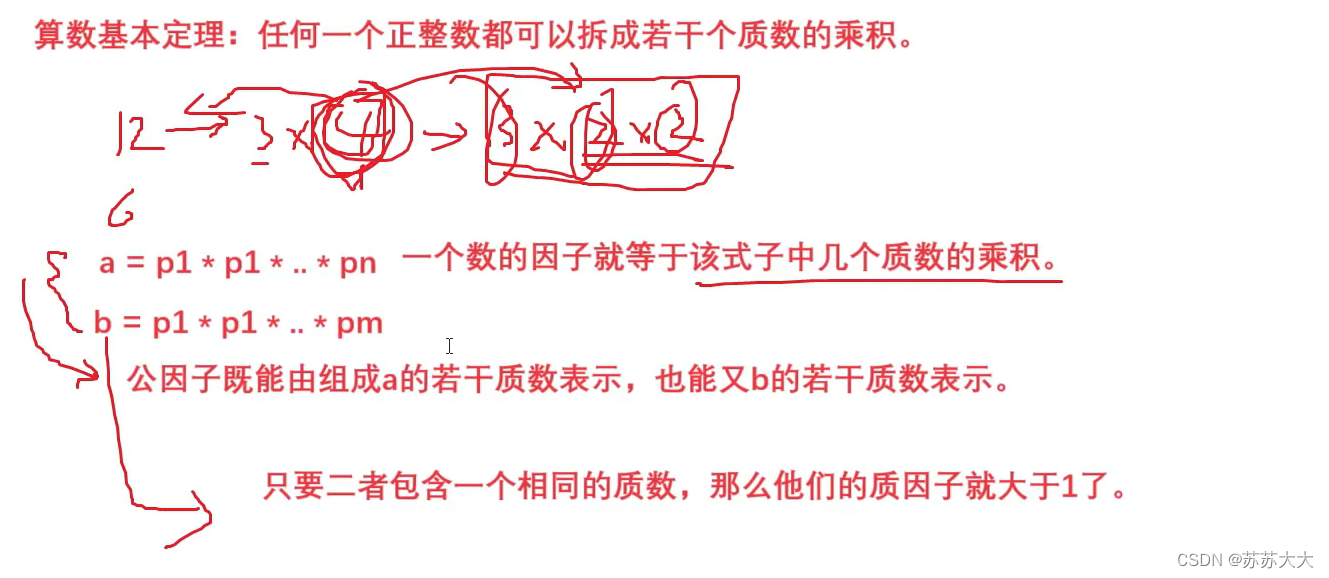
蓝桥杯刷题-12-公因数匹配-数论(分解质因数)不是很理解❓❓
蓝桥杯2023年第十四届省赛真题-公因数匹配 给定 n 个正整数 Ai,请找出两个数 i, j 使得 i < j 且 Ai 和 Aj 存在大于 1 的公因数。 如果存在多组 i, j,请输出 i 最小的那组。如果仍然存在多组 i, j,请输出 i 最小的所有方案中 j 最小的那…...
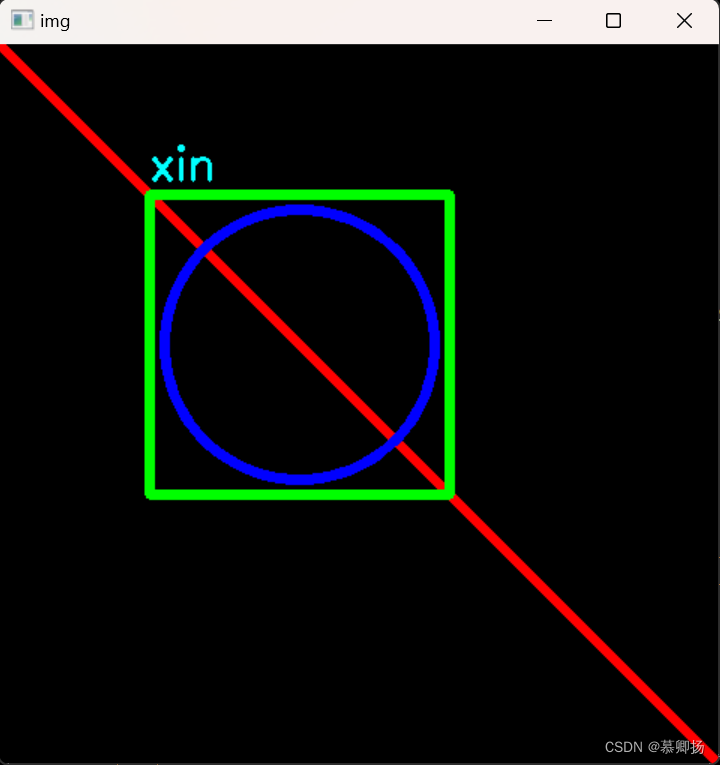
机器视觉学习(十二)—— 绘制图形
目录 一、绘制函数参数说明 1.1 cv2.line()绘制直线 1.2 cv2.rectangle()绘制矩形 1.3 cv2.circle() 绘制圆形 1.4 cv2.ellipse()绘制椭圆 1.5 cv2.polylines()绘制…...

软考信息处理技术员2024年5月报名流程及注意事项
2024年5月软考信息处理技术员报名入口: 中国计算机技术职业资格网(http://www.ruankao.org.cn/) 2024年软考报名时间暂未公布,考试时间上半年为5月25日到28日,下半年考试时间为11月9日到12日。不想错过考试最新消息的…...

linux:du和df区别
文章目录 1. 概述2. du 命令2. df 命令3. 区别总结 1. 概述 du 和 df 都是 Linux 系统中用于查看磁盘空间使用情况的命令,但它们的功能和用法有所不同。 2. du 命令 du 是 “disk usage” 的缩写,用于显示文件或目录的磁盘使用情况。du 命令用于查看指…...
MacOS Docker 部署 Redis 数据库
一、简介 Redis是一个开源的、使用C语言编写的、基于内存亦可持久化的Key-Value数据库,它提供了多种语言的API,并支持网络交互。Redis的数据存储在内存中,因此其读写速度非常快,每秒可以处理超过10万次读写操作,是已知…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
