一元导数与多元求导数总结
前序:文章结构

1.一元导数
①一般函数求导
因为太简单的原因,事实上一般函数求导不会单独出现,大多数都是出现在各种特殊的求导过程中。只要掌握16个基本求导公式没问题。

②复合函数求导(主要链式法则)
这种一般是各种初等函数相互复合包含。
③隐函数求导
方法一:可以两边同时对x求导,然后表示为dy/dx=…的形式即可
方法二:可以利用多元函数中的公式如下。
方法三:一元微分形式不变性。



④反函数求导
即反函数的导数=原函数导数的倒数。
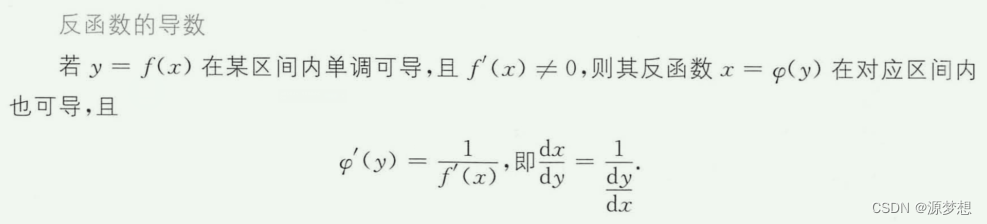
⑤参数方程求导
注意:二阶导的时候,要除以x对t求导。

⑥对数函数求导法
当含有根号,或者很”难受“的次幂时候,可以同时取对数简化求导过程。


⑦分段函数求导
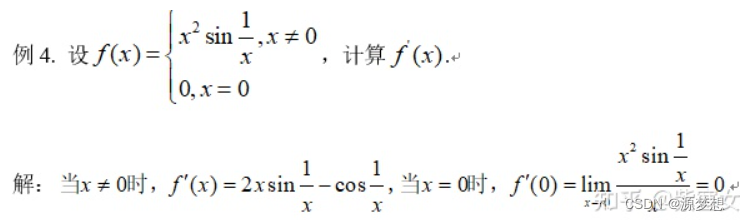
⑧高阶导数
正常求…
2.多元函数求导
①一般函数偏导数
本质就是一元函数导数。
②复合函数偏导数
本质就是一元函数复合导数。
③隐函数偏导数
1.有一个方程F(x,y,z)=0确定的
方法1:两边同时对x求导。
方法2:用公式偏z/偏x=-F’x/F’z
方法3:全微分形式不变性。
2.有一个方程组F(x,y,z,u,v)=0,G(x,y,z,u,v)=0确定的
两个方程两边同时对x求导,将偏u/偏x,偏v/偏x看作变量。利用克莱姆法则解方程组。
④高阶偏导数及混合偏导
注意高阶偏导虽然简单,单数特别容易出错。如下题:


⑤全微分
分别求x,y偏导带入即可。
3.函数求导几点注意例题
①一元参数方程求二阶导一定是:一阶导对t求导/x对t求导(不要忽略分母,我们很容易惯性认为简单在对t求导就好了。)
②多元偏导注意:是多元函数才写下标,才是偏导:形如f(x/y),f(xy)等都是一元函数千万不要出现f’x,f’y,f’1,f’2等字眼
③多元隐函数求导注意点1:
方法一:形如u+eu=xy如果隐函数两边同时对x求导,则u为x,y的函数即u=(x,y)。
方法二:形如u+eu=xy如果用公式:偏U/偏x=-F’x/F’u。这个时候u=C,C为常数
④多元函数求导,如果未指明谁是谁的函数,如y是x的函数y=(x),则xy对x求导为y,即(xy)‘=y,而非y+xy’
⑤多元隐函数求导注意点2:有时隐函数F(x,y,z)=0但是我们不知道谁对谁的偏导(很多时我们可以看出是Z对x或y的偏导),这时可以根据题目F’z(x0,y0,z0)!=0判断
相关文章:

一元导数与多元求导数总结
前序:文章结构 1.一元导数 ①一般函数求导 因为太简单的原因,事实上一般函数求导不会单独出现,大多数都是出现在各种特殊的求导过程中。只要掌握16个基本求导公式没问题。 ②复合函数求导(主要链式法则) 这种一般是…...

通过堆栈分析深拷贝、浅拷贝、赋值的差异
前言数据类型分为:基本数据类型String、Number、Boolean、Null、Undefined、Symbol对象数据类型Object、Array基本数据类型的特点:直接存储在栈(stack)中的数据引用数据类型的特点:存储的是该对象在栈中引用,真实的数据存放在堆内…...

网络割接概述
网络割接概述割接背景企业网络的变化割接概述割接难点割接的操作流程情景模拟及解决方案常见的割接场景割接背景 随着企业业务的不断发展,企业网络为了适应业务的需求不断的改造和优化。无论是硬件的扩容、软件的升级、配置的变更,凡是影响现网运行业务…...
)
开放开源开先河(下)
目录 1.唯一性定义品牌 2.打造爆款塑造品牌 3.生态系统传播品牌 打造爆款塑造品牌 目前全球100多个开源基金会大部分都在美国,已成功孵化了800多个项目。而开放原子开源基金会现有136家捐赠单位,2020年9月,百度将区块链项目超级链࿰…...
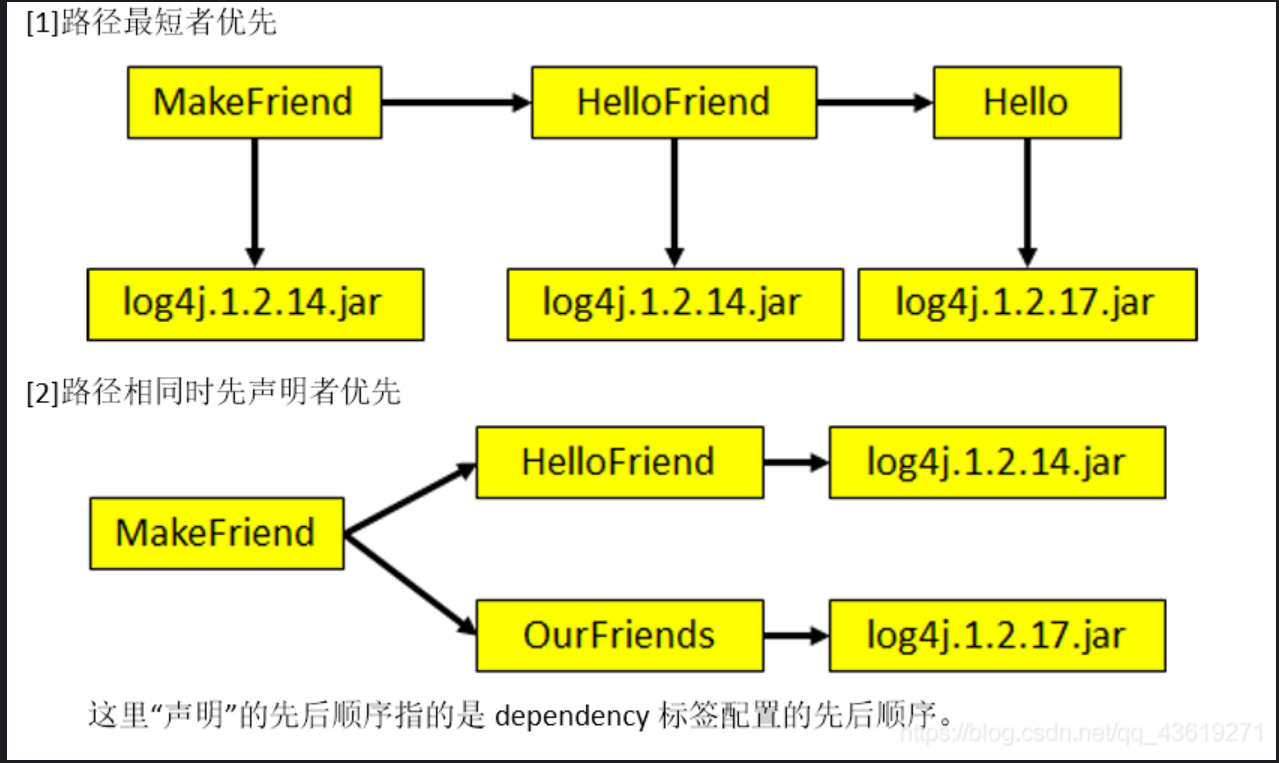
maven的学习
为啥要用maven 1、不用认为添加jar包所依赖的其他jar包 2、能在本地仓库只保留一份jar包,避免了多个工程使用相同jar包,需要重复导入的问题,减少冗余 3、能够规范添加jar包,在下载需要的jar包时有多种方法,但是不能保…...

从前端到后端全面解析文件上传
从前端到后端全面解析文件上传1.前端准备(vueelement-ui)2.后端准备(SpringBootminiomysql)2.1解决跨域2.2配置minio与mysql2.3controller层2.4service层1.前端准备(vueelement-ui) <!DOCTYPE html> <html lang"en"> <head><meta charset"…...

全网火爆,软件测试面试题大全,接口测试题+回答 (18k+的offer)
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 面试测试工程师的时…...

【iOS】—— 浅看block源码
block 文章目录block如何通过终端clang生成源码cpp文件block实质截获自动变量全局变量和静态变量的截获__block说明符iOS开发“强弱共舞”——weak和strong配套使用解决block循环引用问题如何通过终端clang生成源码cpp文件 之前在学习block中学习的比较浅,只看了oc…...

I.MX6ULL_Linux_系统篇(23) busybox文件系统构建
Linux“三巨头”已经完成了 2 个了,就剩最后一个 rootfs(根文件系统)了,本章我们就来学习一下根文件系统的组成以及如何构建根文件系统。这是 Linux 移植的最后一步,根文件系统构建好以后就意味着我们已经拥有了一个完整的、可以运行的最小系…...

shpjs将.zip文件转成geoJson
一、npm install shpjs二、import shp from shpjs三、async setLayerSource() {const geoJsonData await shp(dataUrl)}一直报错:是因为Buffer这个插件一直没找到Uncaught Error: nodebuffer is not supported by this browser解决办法npm install node-polyfill-w…...

eBay是不是一定要养号?是的
相信每个运营过eBay的用户遇到过这个棘手的问题,eBay个人账户的刊登数量是有限的,尤其是新账户只有5个sku,所以一开始的运营会比较艰难。想要快点走上正轨的话,就一定要去注重这个“养号”。eBay运营模式 1.拍卖 eBay最开始是一个…...
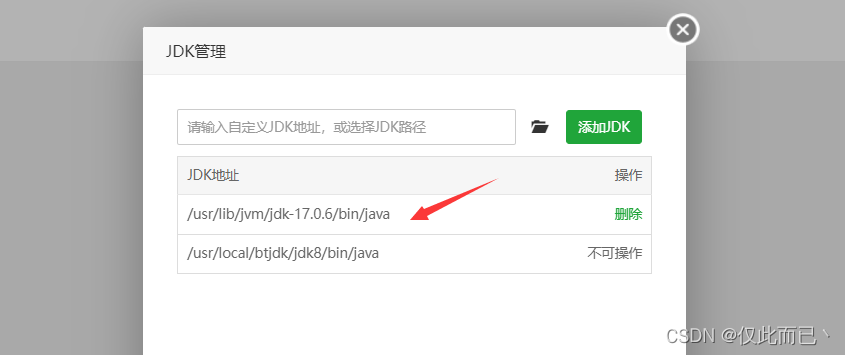
宝塔(二):升级JDK版本
目录 背景 一、下载JDK17 二、配置环境变量 三、配置新的JDK路径 背景 宝塔的软件商店只有JDK8,不满足我当前项目所需的JDK版本,因此想对JDK版本进行升级,升级为JDK17。 一、下载JDK17 先进入 /usr/lib/jvm 目录 点击终端,进…...
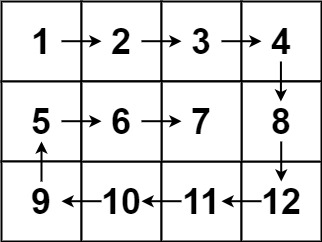
【LeetCode】螺旋矩阵 [M](数组)
54. 螺旋矩阵 - 力扣(LeetCode) 一、题目 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,…...

实验二:动态规划
1.双11的红包雨 问题描述 双11到了,据说这2天会下红包雨,每个红包有不同的价值,小k好开心,但有个规则,就只能接掉落在他身旁的10米范围内的红包(0-10这11个位置)。小k想尽可能的多抢红包&…...

华为机试 HJ27 查找兄弟单词
题目链接:https://www.nowcoder.com/practice/03ba8aeeef73400ca7a37a5f3370fe68?tpId37&tqId21250&rp1&ru/exam/oj/ta&qru/exam/oj/ta&sourceUrl%2Fexam%2Foj%2Fta%3Fdifficulty%3D3%26page%3D1%26pageSize%3D50%26search%3D%26tpId%3D37%26t…...

佩戴舒适的蓝牙耳机有哪些?佩戴舒适的蓝牙耳机推荐
音乐对许多人而言,都是一种抚慰生命的力量,特别是在上下班的时候,在熙熙攘攘的人流中,戴着耳机听一首动听的曲子,无疑会让人心情变得更加舒畅,要想获得出色的音乐体验,没有一副出色的耳机可不行…...
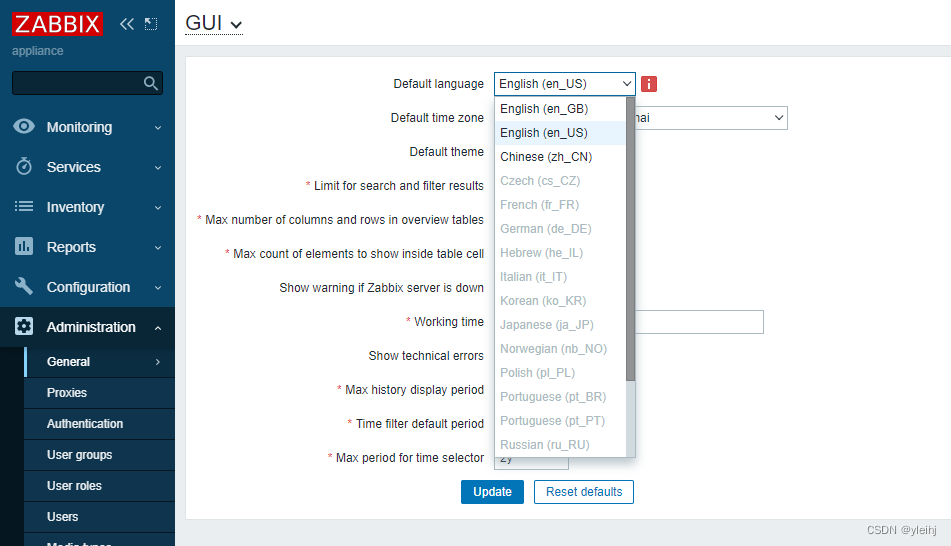
ESXI主机安装Zabbix 6.2
1:首先下载Zabbix Appliance 2:还需要下载VMware converter ,这个需要VMware的账号,或者从其他地方下载也可以。 3:vmdk格式的 image 可直接在 VMware Player、 Server 和 Workstation 产品中使用。要在 ESX,、ESXi 和 vSphere 中…...
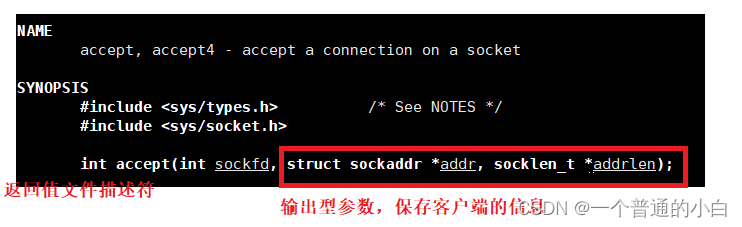
【Linux 网络编程1】使用UDP/TCP编写套接字,多进程/多线程版本的TCP编写的套接字,将套接字封装
目录 1.学习网络编程前的一些基础知识 2.UDP(user datagram protocol)协议的特点 3.使用有UPD编写套接字 4.使用TCP编写套接字 4.2.TCP客服端 4.3.TCP服务器端 4.4.单进程版本(没有人会使用) 4.5.多进程版本 4.6.多线程版本 5.把套接字封装 1…...
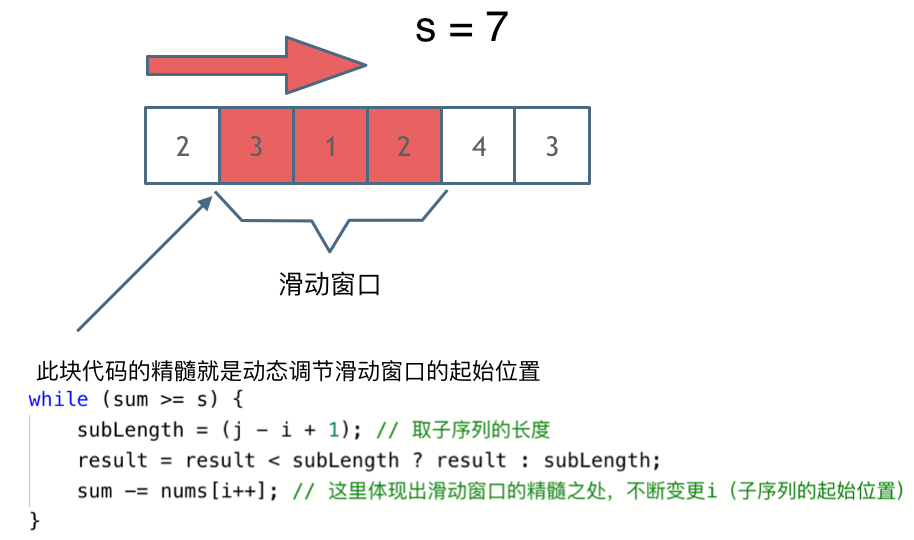
滑动窗口求最大和最小
滑动窗口 要区分最小和最大滑窗,内层while循环的条件和更新结果的地方 核心: 关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。 最小滑窗 给定数组 nums࿰…...

跟ChatGPT学量化,菜鸟炒股也不怕
你是一个python资深量化开发工程师,请介绍量化交易的基本框架 量化交易的基本框架包括以下几个步骤: 数据获取:获取市场数据和公司财务数据等,可以使用API接口、爬虫等方式获取。数据清洗和预处理:对获取到的数据进行清…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
