实验二:动态规划
1.双11的红包雨
问题描述
双11到了,据说这2天会下红包雨,每个红包有不同的价值,小k好开心,但有个规则,就只能接掉落在他身旁的10米范围内的红包(0-10这11个位置)。小k想尽可能的多抢红包,这样就可以去买一个华为手机,小k每秒种只能在移动不超过一米的范围内接住红包。小k一开始站在5这个位置,因此在第一秒,他只能接到4,5,6这三个位置中其中一个位置上的红包。问小k最多可能接到多少价值的红包?
输入
第一行输入整数n,表示共有多少个红包,n<1000;
后面n行表示n个红包,每行有三个整数,分别表示红包掉落的位置、时间和价值。
输出
小k接到的红包价值之和。
输入样例
8
3 18 5
7 13 7
1 8 10
2 7 13
10 20 1
3 17 8
10 2 123
3 13 45
输出样例
81
每个时刻的状态只有三种
-
继续站在原地
-
向左移动
-
向右移动
此外还要注意一点,在0处不能向左移动,在11处不能向右移动。
状态转移方程
dp[i][j]=maxn(dp[i+1][j−1],dp[i+1][j],dp[i+1][j+1])+dp[i][j]dp[i][j]=maxn(dp[i+1][j-1],dp[i+1][j],dp[i+1][j+1])+dp[i][j] dp[i][j]=maxn(dp[i+1][j−1],dp[i+1][j],dp[i+1][j+1])+dp[i][j]
#include<bits/stdc++.h>
using namespace std;int dp[1010][12]; // dp[i][j]表示i时刻j位置开始出发,到最终时间点所获得的最大红包数
//两个数中的最大值
int max_2(int a, int b)
{return (a>b) ? a :b;
}
//三个数中的最大值
int maxn(int a, int b, int c)
{int max = (a>b) ? a : b;return (max>c) ? max : c;
}
// 计算最优值
// 状态转移方程为:dp[i][j]=maxn(dp[i+1][j-1],dp[i+1][j],dp[i+1][j+1])
void maxValue(int max_time)
{//对于每个时间所有位置从结束计算到开头//当记录了上一时刻的最大值,可以以此为参照,计算出所有位置该时刻的最大值//两重循环之后可以获取所有位置所有时刻的最大值for(int i=max_time-1; i>=0; i--){for(int j=0; j<12; j++){if(j == 0) // 在第0位置,下一秒只能原地或向右移动 dp[i][j] = max_2(dp[i+1][j],dp[i+1][j+1]) + dp[i][j];else if(j == 11) // 在第11位置,下一秒只能原地或向左移动 dp[i][j] = max_2(dp[i+1][j],dp[i+1][j-1]) + dp[i][j];else// 其他情况,每个时刻能够向左右或者不动dp[i][j] = maxn(dp[i+1][j-1],dp[i+1][j],dp[i+1][j+1])+ dp[i][j];}}
}
int main()
{int n;cin >> n;int location, time, value;int max_time = -1;memset(dp, 0, sizeof(dp));// 保存输入的数据到数组中 while(n--){cin >> location >> time >> value;dp[time][location] = value;if(time > max_time) max_time = time;}// 求出最大的红包maxValue(max_time);// dp[1][4]为初始时刻、初始位置对应的价值,已经从最后时刻推回来了,所以一定是最优解。cout << dp[1][4] << endl;return 0;
}
2.最大连续字段和
问题描述:略
只有两种情况:
- 某位置最大连续子段为它本身
- 最大连续子段长度至少为 2(至少包含它之前的一个节点)
取两者的最大值,递推方程:
dp[i]=max(dp[i−1]+arr[i],arr[j])dp[i]=max(dp[i-1]+arr[i],arr[j]) dp[i]=max(dp[i−1]+arr[i],arr[j])
#include<bits/stdc++.h>
using namespace std;
int main()
{int num;cin>>num;int arr[num],dp[num]; // 读数据for(int i=0;i<num;i++){ cin>>arr[i];dp[i]=0;}// 初始化dp[0]=max(arr[0],0);for(int i=1;i<num;i++){// 状态转移方程dp[i]=max(arr[i],dp[i-1]+arr[i]); }sort(dp,dp+num);//排序cout<<dp[num-1];//输出最大值 return 0;
}
3.减肥的小k 2
题目描述
小K是个苦命的孩子,他的师傅为了多赚钱,以减肥为理由,让他去采药,并说不完成不能吃饭。野地里有许多不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。要求在规定的时间t里,采到的草药的总价值最大。
输入
第一行有2个整数T(1≤T≤1000)和M(1≤M≤100),一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。
输出
1个整数,表示在规定的时间内可以采到的草药的最大总价值。
输入样例
70 3
71 100
69 1
1 2
输出样例
3
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005; // 最大草药数量
const int MAXT = 1005; // 最大采药时间
int t[MAXN], v[MAXN]; // t[i]是第i个草药的采摘时间,v[i]是第i个草药的价值
int dp[MAXT]; // dp[j]表示用j的时间采摘草药的最大价值
int main()
{int T, M;cin >> T >> M; // T是总时间,M是草药数量for (int i = 1; i <= M; i++){cin >> t[i] >> v[i]; // 输入每个草药的采摘时间和价值}memset(dp, 0, sizeof(dp)); // 初始化dp数组为0for (int i = 1; i <= M; i++){for (int j = T; j >= t[i]; j--){// 从后往前遍历,防止重复计算dp[j] = max(dp[j], dp[j-t[i]]+v[i]); // 状态转移方程}}cout << dp[T] << endl; // 输出用T的时间采摘草药的最大价值return 0;
}
4.最长非连续公共子序列
题目描述
略
dp [ i ] [ j ] 表示第一个串前 i 个与第二个串前 j 个组成的 lcs 子问题
状态转移方程:
如果当前指针两个字符相同:
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1] + 1 dp[i][j]=dp[i−1][j−1]+1
如果当前指针两个字符不同:
需要从前面的两个状态恢复,两个状态分别为 dp [ i-1 ] [ j ] 和 dp [ i ] [ j-1 ] ,将它们的最大值作为该位置的状态
dp[i][j]=max(dp[i−1][j],dp[i][j−1])dp[i][j] = max(dp[i-1][j], dp[i][j-1]) dp[i][j]=max(dp[i−1][j],dp[i][j−1])
#include<bits/stdc++.h>
using namespace std;
int lcs(string s1, string s2)
{// 初始化int m = s1.size();int n = s2.size();int dp[m+1][n+1];memset(dp, 0, sizeof(dp));// 对于a,b两个字符串,分别设定两个指针a,b// 指针分别从头开始向后移动,取两个字符串前i,j个// 这样就存在两种情况// 1.两个指针处的字符相同说明存在子串,dp[i][j] = dp[i-1][j-1] + 1 从ab指针同时退后两个的情况+1// 2.如果两个指针指向的字符不相同,说明不能从 i-1,j-1 跳转到 i,j,但是为了保存之前的结果,需要存储当前// 的最优解,当前是将两个指针同时前进1个单位,最优解一定在左指针前进一个或右指针前进一个里面选// 这就推出了最终的状态转移方程for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (s1[i-1] == s2[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}}}return dp[m][n];
}
int main()
{string s1 = "ABCD";string s2 = "ABDE";cout << lcs(s1, s2) << endl; // 输出 2,即 "AB" 是最长非连续公共子序列return 0;
}
5.切钢条
题目描述
一家公司购买长钢条,将其切割成短钢条出售,切割本身没有成本,长度为i的短钢条的价格为Pi。那给
定一段长度为n的钢条和一个价格表Pi,求钢条的切割方案使得收益Rn最大。

输入要求
输入钢条的长度n。
输出要求
输出获得的最大收益。
dp [ i ] 表示长度为 i 的情况下的最大利润
共有 10 种切法,所以要设置两重循环,目的是获得每个长度下的最优解,有了小长度才能以此为基础获取大长度的最优解
有两种状态,切或不切,切掉之后要考虑价值是否增加,所以产生了状态转移方程:
dp[i]=max(pi[j]+dp[i−j],dp[i])dp[i] = max(pi[j] + dp[i - j], dp[i]) dp[i]=max(pi[j]+dp[i−j],dp[i])
#include<bits/stdc++.h>
using namespace std;
int pi[11] = { 0,1,5,8,9,10,17,17,20,24,30 }; //记录已知长度钢条价值
int dp[1000] = { 0 };//记录动态规划结果
int findMaxVal(int n)
{if (n == 0) // 若n为0直接返回return 0;for (int i = 1;i <= n;i++) {for (int j = 1;j <= i && j <= 10;j++) { // 第一刀最多切10种dp[i] = max(pi[j] + dp[i - j], dp[i]);//遍历所有切法}}return dp[n];
}
int main()
{int n;cin >> n;memset(dp,0,sizeof(dp));// 判断一下是否超过10,记录除数和余数int chushu = 0;int yushu = 0;int res_10 = 0;int res = 0;if(n>10){chushu = n / 10;yushu = n % 10;res_10 = findMaxVal(10);res_10 *= chushu;res = res_10 + findMaxVal(yushu);}else{res = findMaxVal(n); }cout << res << endl;return 0;
}
6.合格的盗贼
题目描述
一条街上有N个商铺;商铺i有价值V[i]的物品,你有足够的时间在晚上光顾所有的商店,人们称呼你为盗贼;每个商店都有一个报警器,会在晚上报警,但是只有相邻的2个商店同时报警时,警察才会出动;你需要证明你是个合格的盗贼。
输入要求
第一行一个整数N<=100,商店数。
第二行N个整数,每个商店的价值
输出要求
输出偷盗的最大价值。
假设在考虑第i个,只有两种个情况,只有这两种情况收益最大,按照这种思想往下推很简单就能求出最大利润
- 第一种,i,i - 2
- 第二种,i - 1
#include<bits/stdc++.h>
using namespace std;
int dp[101] = { 0 };
int findMaxValue(int n)
{if (n == 1)return dp[0];else if (n == 2)return max(dp[0], dp[1]);dp[1] = max(dp[0], dp[1]);for (int i = 3;i <= n;i++){// 只有两种选择,假设有 a b c 三个连续的位置// 只有两种选择不会触发警报// 1. a c// 2. b// 依据这个限制条件可以给出状态转移方程dp[i - 1] = max(dp[i - 2], dp[i - 3] + dp[i - 1]);}return dp[n - 1];
}
int main()
{int n;cin >> n;for (int i = 0;i < n;i++) {cin >> dp[i];}int res = findMaxValue(n);cout << res << endl;return 0;
}
相关文章:

实验二:动态规划
1.双11的红包雨 问题描述 双11到了,据说这2天会下红包雨,每个红包有不同的价值,小k好开心,但有个规则,就只能接掉落在他身旁的10米范围内的红包(0-10这11个位置)。小k想尽可能的多抢红包&…...

华为机试 HJ27 查找兄弟单词
题目链接:https://www.nowcoder.com/practice/03ba8aeeef73400ca7a37a5f3370fe68?tpId37&tqId21250&rp1&ru/exam/oj/ta&qru/exam/oj/ta&sourceUrl%2Fexam%2Foj%2Fta%3Fdifficulty%3D3%26page%3D1%26pageSize%3D50%26search%3D%26tpId%3D37%26t…...

佩戴舒适的蓝牙耳机有哪些?佩戴舒适的蓝牙耳机推荐
音乐对许多人而言,都是一种抚慰生命的力量,特别是在上下班的时候,在熙熙攘攘的人流中,戴着耳机听一首动听的曲子,无疑会让人心情变得更加舒畅,要想获得出色的音乐体验,没有一副出色的耳机可不行…...
ESXI主机安装Zabbix 6.2
1:首先下载Zabbix Appliance 2:还需要下载VMware converter ,这个需要VMware的账号,或者从其他地方下载也可以。 3:vmdk格式的 image 可直接在 VMware Player、 Server 和 Workstation 产品中使用。要在 ESX,、ESXi 和 vSphere 中…...
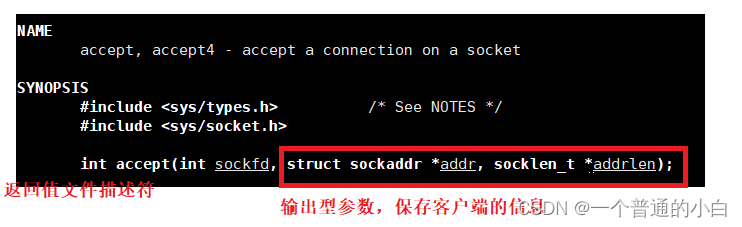
【Linux 网络编程1】使用UDP/TCP编写套接字,多进程/多线程版本的TCP编写的套接字,将套接字封装
目录 1.学习网络编程前的一些基础知识 2.UDP(user datagram protocol)协议的特点 3.使用有UPD编写套接字 4.使用TCP编写套接字 4.2.TCP客服端 4.3.TCP服务器端 4.4.单进程版本(没有人会使用) 4.5.多进程版本 4.6.多线程版本 5.把套接字封装 1…...
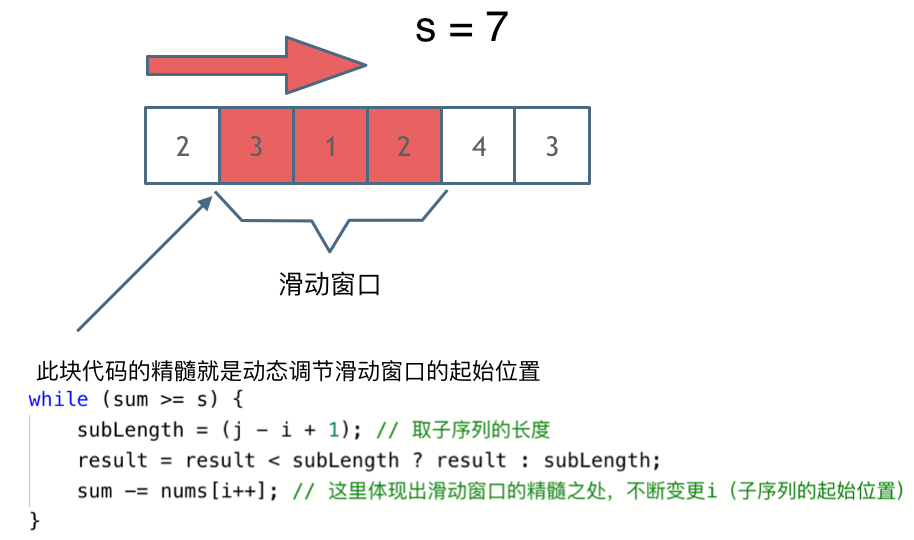
滑动窗口求最大和最小
滑动窗口 要区分最小和最大滑窗,内层while循环的条件和更新结果的地方 核心: 关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。 最小滑窗 给定数组 nums࿰…...

跟ChatGPT学量化,菜鸟炒股也不怕
你是一个python资深量化开发工程师,请介绍量化交易的基本框架 量化交易的基本框架包括以下几个步骤: 数据获取:获取市场数据和公司财务数据等,可以使用API接口、爬虫等方式获取。数据清洗和预处理:对获取到的数据进行清…...

扬帆优配|2600亿新能源巨头狂飙!外资唱多中国:再涨15%
全国停摆的危机,正在迫临法国。 大停工正在将法国推向风险境地。法国政府估计,当地时间3月7日,将迸发全国大型停工游行。法国总工会宣告,到时将让全法国停摆。法国担任交通业务的部长级代表克莱蒙博讷正告称,7日将成为…...
ChatGPT技术与商业模式及产业发展布局方案
文章目录模块一:概念模块二:架构模块三:技术模块四:算力模块五:体验模块六:应用模块七:商业模块八:产业模块九:建议结语主要内容: 采用模块化教学方法&#x…...

CIMCAI port ai shipping ai artificial intelligence smart port
上海人工智能独角兽中集集团高科技中集飞瞳,是全球应用落地最广,规模最大,最先进的的港航人工智能高科技企业,工业级成熟港航人工智能产品全球规模化落地应用,全球前三大船公司及港口码头应用落地。上海人工智能独角兽…...
《数据解构》HashMap源码解读
👑作者主页:Java冰激凌 📖专栏链接:数据结构 目录 了解HashMap HashMap的构造 两个参数的构造方法 一个参数的构造方法 不带参数的构造方法 哈希表初始化的长度 HashMap源码中的成员 Pt Get 了解HashMap 首先我们要明…...

Databend 开源周报 第 83 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.com 。Whats New探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。Support for WebHDFSHDFS 是大数…...
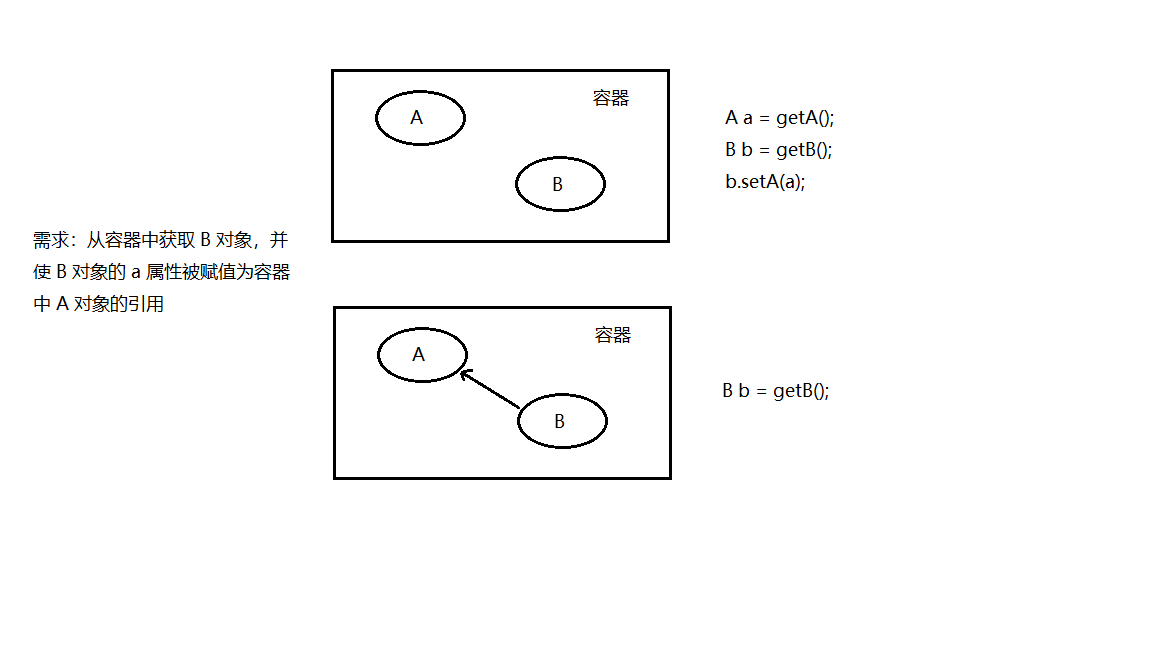
Spring | 基础
1. IOC和DI IOC:控制反转,其思想是反转资源获取的方向,传统的资源查找方式要求组件向容器发起请求查找资源,作为回应,容器适时的返回资源。而应用了 IOC 之后,则是**容器主动地将资源推送给它所管理的组件…...

windows7安装sql server 2000安装步骤 及安装过程中遇到的问题和解决方式
提示:文章写完后windows7安装sql server 2000安装步骤 及安装过程中遇到的问题和解决方式, 文章目录一、ms sql server 2000是什么?版本简介:**特点:****优点:**二、步骤1.下载安装包及Sq4补丁包2.安装 ms …...

Python 开发-批量 FofaSRC 提取POC 验证
数据来源 学习内容和目的: ---Request 爬虫技术,lxml 数据提取,异常护理,Fofa 等使用说明---掌握利用公开或 0day 漏洞进行批量化的收集及验证脚本开发Python 开发-某漏洞 POC 验证批量脚本---glassfish存在任意文件读取在默认4…...

Linux系统中部署软件
目录 1.Mysql 2.Redis 3.ZooKeeper 声明 致谢 1.Mysql 参考:CentOS7安装MySQL 补充: ① 执行:rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022 再执行:yum -y install mysql-community-server ② mysql…...

PHP常用框架介绍与比较
HP是一种广泛应用于Web开发的编程语言。随着互联网的快速发展,PHP的应用场景变得越来越广泛,从简单的网站到复杂的Web应用程序都可以使用PHP来开发。为了更好地组织和管理PHP代码,开发人员经常会使用框架来提高开发效率和代码质量。 本文将介绍一些常用的PHP框架,并进行简…...

Umi + React + Ant Design Pro 项目实践(一)—— 项目搭建
学习一下 Umi、 Ant Design 和 Ant Design Pro 从 0 开始创建一个简单应用。 首先,新建项目目录: 在项目目录 D:\react\demo 中,安装 Umi 脚手架: yarn create umi # npm create umi安装成功: 接下来,…...
)
MySQL知识点总结(1)
目录 1、sql、DB、DBMS分别是什么,他们之间的关系? 2、什么是表? 3、SQL语句怎么分类呢? 4、导入数据 5、什么是sql脚本呢? 6、删除数据库 7、查看表结构 8、表中的数据 10、查看创建表的语句 11、简单的查询…...
)
day45第九章动态规划(二刷)
今日任务 70.爬楼梯(进阶)322.零钱兑换279.完全平方数 70.爬楼梯(进阶) 题目链接: https://leetcode.cn/problems/climbing-stairs/description/ 题目描述: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
