Golang | Leetcode Golang题解之第18题四数之和
题目:

题解:
func fourSum(nums []int, target int) (quadruplets [][]int) {sort.Ints(nums)n := len(nums)for i := 0; i < n-3 && nums[i]+nums[i+1]+nums[i+2]+nums[i+3] <= target; i++ {if i > 0 && nums[i] == nums[i-1] || nums[i]+nums[n-3]+nums[n-2]+nums[n-1] < target {continue}for j := i + 1; j < n-2 && nums[i]+nums[j]+nums[j+1]+nums[j+2] <= target; j++ {if j > i+1 && nums[j] == nums[j-1] || nums[i]+nums[j]+nums[n-2]+nums[n-1] < target {continue}for left, right := j+1, n-1; left < right; {if sum := nums[i] + nums[j] + nums[left] + nums[right]; sum == target {quadruplets = append(quadruplets, []int{nums[i], nums[j], nums[left], nums[right]})for left++; left < right && nums[left] == nums[left-1]; left++ {}for right--; left < right && nums[right] == nums[right+1]; right-- {}} else if sum < target {left++} else {right--}}}}return
}相关文章:

Golang | Leetcode Golang题解之第18题四数之和
题目: 题解: func fourSum(nums []int, target int) (quadruplets [][]int) {sort.Ints(nums)n : len(nums)for i : 0; i < n-3 && nums[i]nums[i1]nums[i2]nums[i3] < target; i {if i > 0 && nums[i] nums[i-1] || nums[i]…...

自动驾驶中的传感器融合算法:卡尔曼滤波器和扩展卡尔曼滤波器
自动驾驶中的传感器融合算法:卡尔曼滤波器和扩展卡尔曼滤波器 附赠自动驾驶学习资料和量产经验:链接 介绍: 追踪静止和移动的目标是自动驾驶技术领域最为需要的核心技术之一。来源于多种传感器的信号,包括摄像头,雷达…...
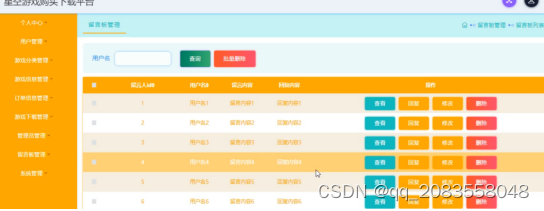
基于ssm的星空游戏购买下载平台的设计与实现论文
摘 要 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势,商品交易当然也不能排除在外,随着商品交易管理的不断成熟,它彻底改变了过去传统的经营管理方式,不仅使商品…...

DSOX6004A是德科技DSOX6004A示波器
181/2461/8938产品概述: 特点: 是德科技DSOX6004A具有7合1集成功能,结合了数字通道、串行协议分析、内置双通道波形发生器、频率响应分析、内置数字万用表和带累加器的内置10位计数器。1千兆赫至6千兆赫4个模拟通道在12.1英寸电容式多点触摸屏上轻松查…...

golang 使用 cipher、aes 实现 oauth2 验证
在Go语言中,crypto/cipher包提供了加密和解密消息的功能。这个包实现了各种加密算法,如AES、DES、3DES、RC4等,以及相应的模式,如ECB、CBC、CFB、OFB、CTR等。以下是如何使用crypto/cipher包进行加密和解密操作的基本步骤…...
LLMs之FreeGPT35:FreeGPT35的简介、安装和使用方法、案例应用之详细攻略
LLMs之FreeGPT35:FreeGPT35的简介、安装和使用方法、案例应用之详细攻略 目录 FreeGPT35的简介 FreeGPT35的安装和使用方法 1、部署和启动服务 Node 2、使用 Docker 部署服务: 运行 Docker 容器以部署服务 使用 Docker Compose 进行更方便的容器化…...

【力扣一刷】代码随想录day32(贪心算法part2:122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II )
目录 【122.买卖股票的最佳时机II】中等题 方法一 贪心算法 方法二 动态规划 【55. 跳跃游戏】中等题 【尝试】 递归 (超时) 方法 贪心算法 【45.跳跃游戏II】中等题 方法 贪心算法 【122.买卖股票的最佳时机II】中等题(偏简单࿰…...
安卓远离手机app
软件介绍 远离手机是专门为防止年轻人上瘾而打造的生活管理类的软件,适度用手机,保护眼睛,节约时间。 下载 安卓远离手机app...
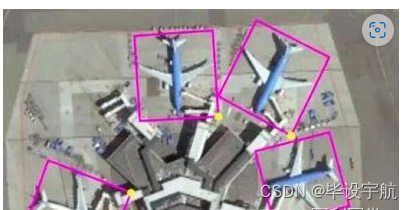
yolov5旋转目标检测遥感图像检测-无人机旋转目标检测(代码和原理)
YOLOv5(You Only Look Once version 5)是一个流行且高效的实时目标检测深度学习模型,最初设计用于处理图像中的水平矩形边界框目标。然而,对于旋转目标检测,通常需要对原始YOLOv5架构进行扩展或修改,以便能…...

云手机提供私域流量变现方案
当今数字营销领域,私域流量是一座巨大的金矿,然而并非人人能够轻易挖掘。一家营销公司面临着利用社交、社区、自媒体等应用积累私域流量,并通过销售产品、推送广告等方式实现流量变现的挑战与困境。本文将详细介绍这家公司是如何通过云手机&a…...

树的基本概念与二叉树
文章目录 树的基本概念与二叉树一、树的概念和结构1. 树的概念2. 树的相关概念 二、树的存储1. 左孩子右兄弟表示法2. 双亲表示法 三、二叉树1. 特殊的二叉树1.1 满二叉树1.2 完全二叉树 树的基本概念与二叉树 一、树的概念和结构 1. 树的概念 树是一种非线性的数据结构,它是…...

什么是物理服务器?
物理服务器又叫做独立服务器,指物理上的单独服务器,是有着实体的服务器并不是虚拟的,物理服务器也可以理解成一台超大的电脑,但是对于普通的家用电脑来说,物理服务器需要长期处于开机的状态,对于硬件性能消…...
数据结构:详解【树和二叉树】
1. 树的概念及结构(了解) 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝…...
“成像光谱遥感技术中的AI革命:ChatGPT在遥感领域中的应用“
遥感技术主要通过卫星和飞机从远处观察和测量我们的环境,是理解和监测地球物理、化学和生物系统的基石。ChatGPT是由OpenAI开发的最先进的语言模型,在理解和生成人类语言方面表现出了非凡的能力。本文重点介绍ChatGPT在遥感中的应用,人工智能…...
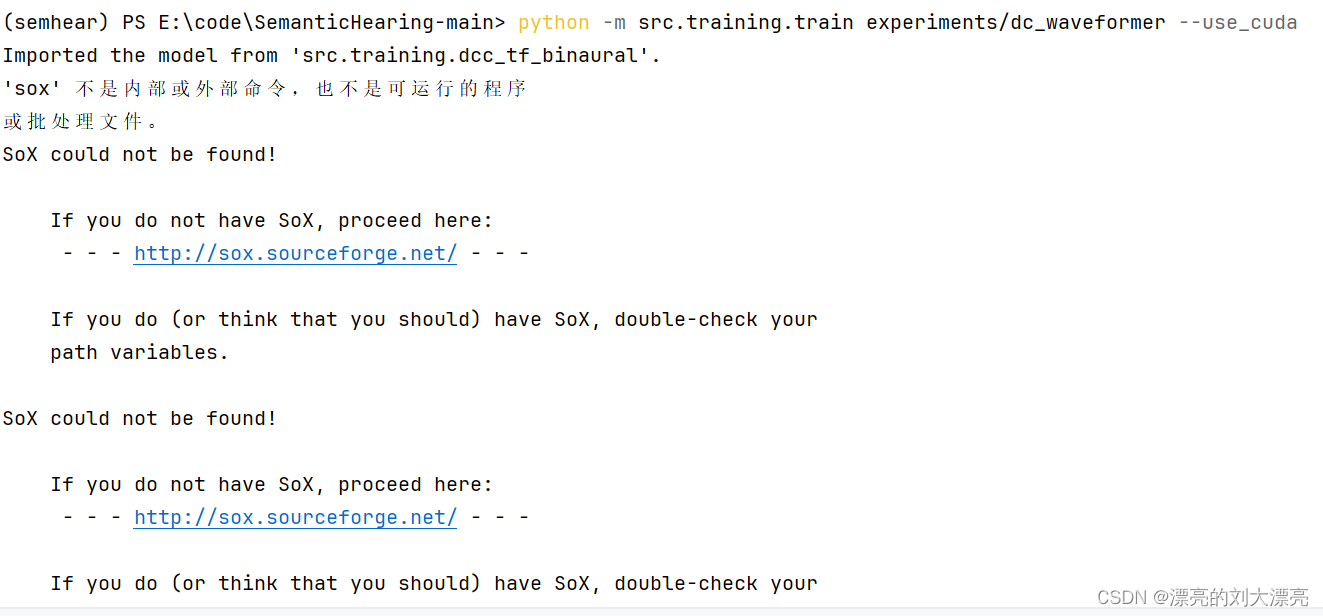
semhear环境sox
这里写自定义目录标题 pip list 看到当前环境下已经有sox了怀疑跟torchaudio和torchvision有关,更新了一下:装了torchvisionsox还是找不到 pip list 看到当前环境下已经有sox了 怀疑跟torchaudio和torchvision有关,更新了一下: p…...

如何快速开启一个项目-ApiHug - API design Copilot
ApiHug101-001开启篇 🤗 ApiHug {Postman|Swagger|Api...} 快↑ 准√ 省↓ GitHub - apihug/apihug.com: All abou the Apihug apihug.com: 有爱,有温度,有质量,有信任ApiHug - API design Copilot - IntelliJ IDEs Plugin |…...

从用友U9到钉钉通过接口配置打通数据
从用友U9到钉钉通过接口配置打通数据 接通系统:用友U9 用友U9cloud深耕制造领域十三载,U9cloud在机械、电子、汽配、家具、整车、军工等细分行业有着深厚的积累,尤其是机械、电子和汽配行业,不但打造了多个成熟的产品模式和应用场…...
PyQt qrc2py 使用PowerShell将qrc文件转为py文件并且将导入模块PyQt或PySide转换为qtpy模块开箱即用
前言 由于需要使用不同的qt环境(PySide,PyQt)所以写了这个脚本,使用找到的随便一个rcc命令去转换qrc文件,然后将导入模块换成qtpy这个通用库(支持pyside2-6,pyqt5-6),老版本的是Qt.py(支持pysi…...
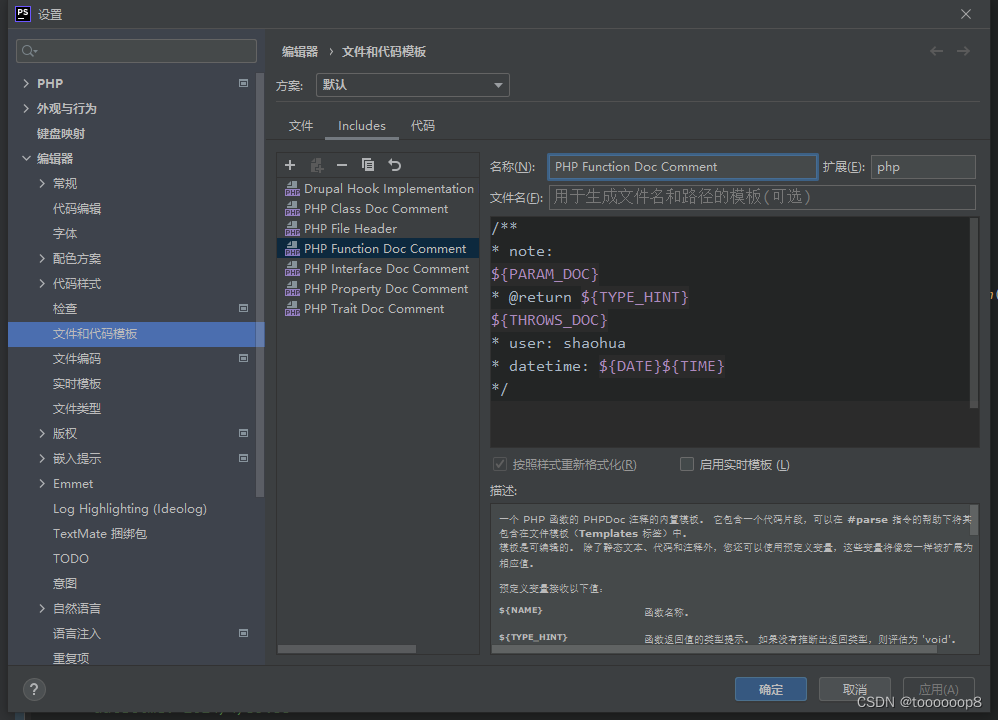
phpstorm设置头部注释和自定义注释内容
先说设置位置: PhpStorm中文件、类、函数等注释的设置在:setting-》Editor-》FIle and Code Template-》Includes-》PHP Function Doc Comment下设置即可,其中方法的默认是这样的: /** ${PARAM_DOC} #if (${TYPE_HINT} ! "…...

【数据分析面试】10. 计算平均通勤时间(SQL:timestampdiff() 和datediff()区别)
题目 假设你在Uber工作。rides表包含了关于Uber用户在美国各地的行程信息。 编写一个查询,以获取纽约(NY)每位通勤者的平均通勤时间(以分钟为单位),以及纽约所有通勤者的平均通勤时间(以分钟为…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

在MobaXterm 打开图形工具firefox
目录 1.安装 X 服务器软件 2.服务器端配置 3.客户端配置 4.安装并打开 Firefox 1.安装 X 服务器软件 Centos系统 # CentOS/RHEL 7 及之前(YUM) sudo yum install xorg-x11-server-Xorg xorg-x11-xinit xorg-x11-utils mesa-libEGL mesa-libGL mesa-…...

Java求职者面试:微服务技术与源码原理深度解析
Java求职者面试:微服务技术与源码原理深度解析 第一轮:基础概念问题 1. 请解释什么是微服务架构,并说明其优势和挑战。 微服务架构是一种将单体应用拆分为多个小型、独立的服务的软件开发方法。每个服务都运行在自己的进程中,并…...
)
GitHub 趋势日报 (2025年06月07日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 603 netbird 459 dify 440 cognee 352 omni-tools 337 note-gen 239 ragbits 237 …...
