Accuracy准确率,Precision精确率,Recall召回率,F1 score
真正例和真反例是被正确预测的数据,假正例和假反例是被错误预测的数据。然后我们需要理解这四个值的具体含义:
TP(True Positive):被正确预测的正例。即该数据的真实值为正例,预测值也为正例的情况;
TN(True Negative):被正确预测的反例。即该数据的真实值为反例,预测值也为反例的情况;
FP(False Positive):被错误预测的正例。即该数据的真实值为反例,但被错误预测成了正例的情况;
FN(False Negative):被错误预测的反例。即该数据的真实值为正例,但被错误预测成了反例的情况。
- 准确率(Accuracy)表示分类正确的样本占总样本个数的比例。
Acc = (TP+TN)/(TP+TN+FP+FN)
Accuracy是衡量分类模型的最直白的指标,但缺陷也是明显的。假设有100个样本,其中有99个都是正样本,则分类器只需要一直预测为正例,就可以得到99%的准确率,实际上这个分类器性能是很低下的。也就是说,当不同类别的样本所占的比例严重不平衡时,占比大的类别会是影响准确率的最主要的因素。所以,只有当数据集各个类别的样本比例比较均衡时,Accuracy这个指标才是一个比较好的衡量标准。因此,必须参考其他指标才能完整评估模型的性能。 - Precision精确率又叫查准率,表示预测结果为正例的样本中实际为正样本的比例
Pre = TP/(TP+FP)
当反例被错误预测成正例(FP)的代价很高时,适合用精确率。根据公式可知,精确率越高,FP越小。比如在垃圾在垃圾邮件检测中,假正例意味着非垃圾邮件(实际为负)被错误的预测为垃圾邮件(预测为正)。如果一个垃圾邮件监测系统的查准率不高导致很多非垃圾邮件被归到垃圾邮箱里去,那么邮箱用户可能会丢失或者漏看一些很重要的邮件。 - Recall召回率又被称为查全率,表示预测结果为正样本中实际正样本数量占全样本中正样本的比例。
Rec = TP/(TP+FN)
当正例被错误的预测为反例(FN)产生的代价很高时,适合用召回率。根据公式可知,召回率越高,FN越小。比如说在银行的欺诈检测或医院的病患者检测中,如果将欺诈性交易(实际为正)预测为非欺诈性交易(预测为负),则可能会给银行带来非常严重的损失。再比如以最近的新冠疫情为例,如果一个患病者(实际为正)经过试剂检测被预测为没有患病(预测为负),这样的假反例或者说假阴性产生的风险就非常大 - F1 score是精确率和召回率的一个加权平均。
F1 = 2 * (P*R/(P+R))
Precision体现了模型对负样本的区分能力,Precision越高,模型对负样本的区分能力越强;Recall体现了模型对正样本的识别能力,Recall越高,模型对正样本的识别能力越强。F1 score是两者的综合,F1 score越高,说明模型越稳健。
相关文章:

Accuracy准确率,Precision精确率,Recall召回率,F1 score
真正例和真反例是被正确预测的数据,假正例和假反例是被错误预测的数据。然后我们需要理解这四个值的具体含义: TP(True Positive):被正确预测的正例。即该数据的真实值为正例,预测值也为正例的情况…...
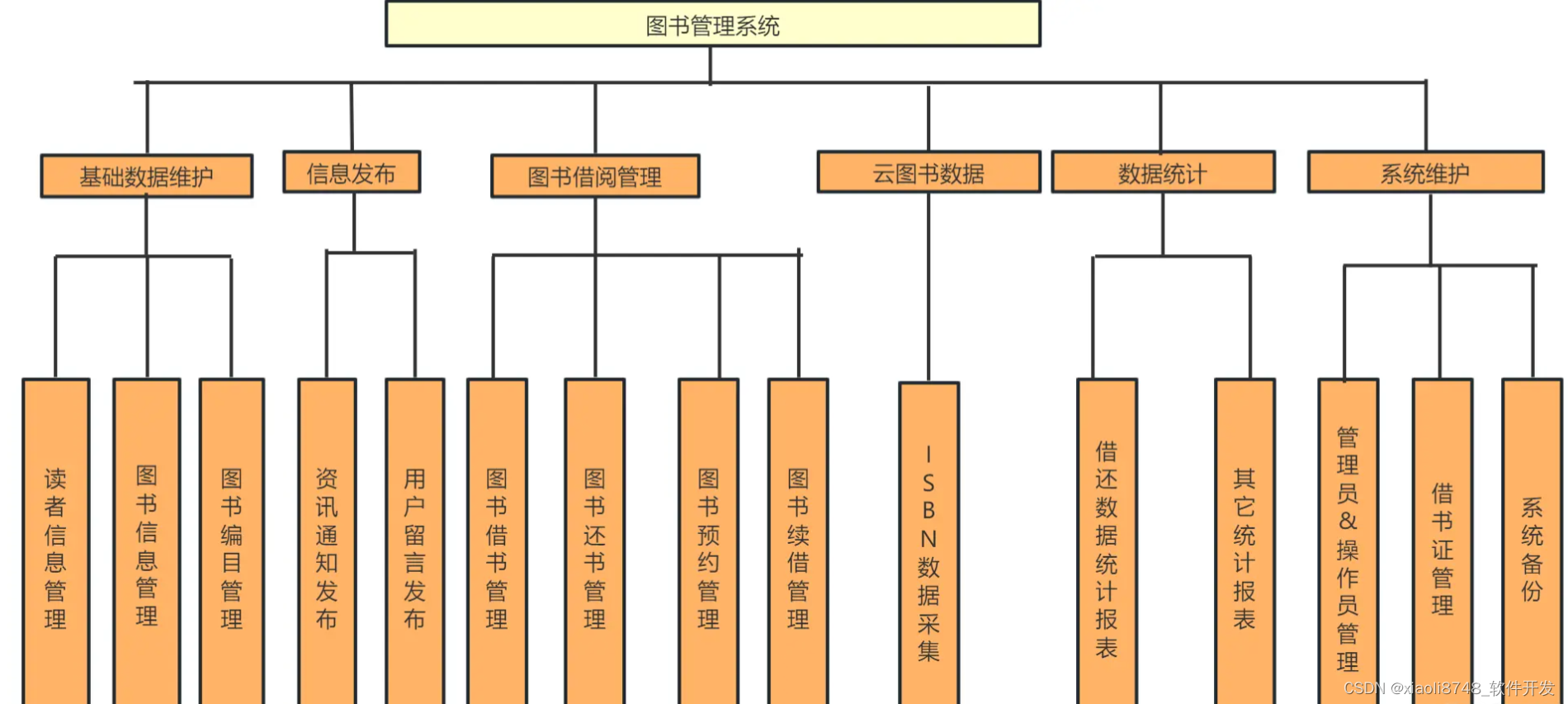
系统架构最佳实践 -- 智慧图书管理系统架构设计
随着数字化时代的到来,智慧图书管理系统在图书馆和机构中扮演着重要的角色。一个优秀的图书管理系统不仅需要满足基本的借阅管理需求,还需要具备高效的性能、良好的扩展性和稳定的安全性。本文将讨论智慧图书管理系统的架构设计与实现,以满足…...

网络基础三——IP协议补充和Mac帧协议
全球网络及网段划分的理解 根据国家组织地区人口综合评估进行IP地址范围的划分; 假设前8位用来区分不同的国家,国际路由器负责全球数据传输,子网掩码为IP/8;次6位区分不同的省份,国内路由器负责全国数据的传输…...
人工智能——深度学习
4. 深度学习 4.1. 概念 深度学习是一种机器学习的分支,旨在通过构建和训练多层神经网络模型来实现数据的高级特征表达和复杂模式识别。与传统机器学习算法相比,深度学习具有以下特点: 多层表示学习:深度学习使用深层神经网络&a…...

postgresql uuid
示例数据库版本PG16,对于参照官方文档截图,可以在最上方切换到对应版本查看,相差不大。 方法一:自带函数 select gen_random_uuid(); 去掉四个斜杠,简化成32位 select replace(gen_random_uuid()::text, -, ); 官网介绍…...
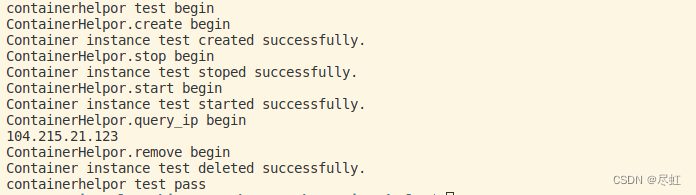
【azure笔记 1】容器实例管理python sdk封装
容器实例管理python sdk封装 测试结果 说明 这是根据我的需求写的,所以有些参数是写死的,比如cpu核数和内存,你可以根据你的需要自行修改。前置条件: 当前环境已安装python3.8以上版本和azure cli并且已经登陆到你的账户 依赖安…...
和又可以异常(Exception)的过滤器)
Nestjs 中定义既可以捕获错误(Error)和又可以异常(Exception)的过滤器
Nestjs 中,使用基于 HttpException 定义过滤器的话,只能捕获 Http 带状态码(statusCode)的 Exception,不能捕获 throw new Error(‘xxx’) 抛出的错误。 以下是使用实现 ExceptionFilter 接口定义的一个不特定于平台(express 或 fastify,即无论使用这两个web服务框架的…...

GitHub 仓库 (repository) Branch - SSH clone URL - Clone in Desktop - Download ZIP
GitHub 仓库 [repository] Branch - SSH clone URL - Clone in Desktop - Download ZIP 1. Branch2. SSH clone URL3. Clone in Desktop4. Download ZIPReferences 1. Branch 显示当前分支的名称。从这里可以切换仓库内分支,查看其他分支的文件。 2. SSH clo…...
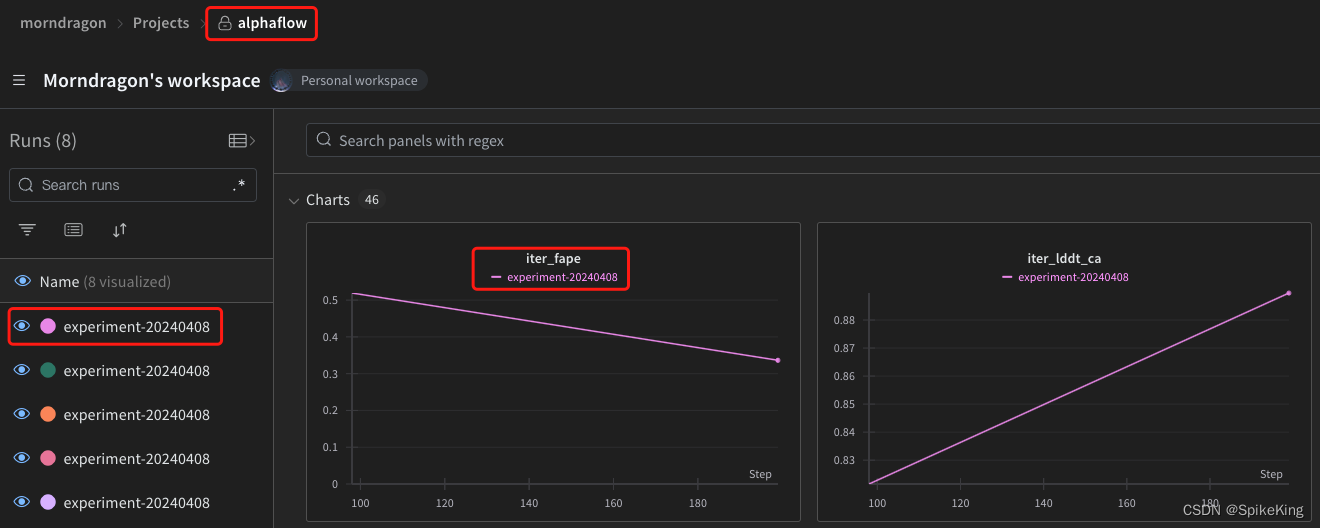
Training - 使用 WandB 配置 可视化 模型训练参数
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/137529140 WandB (Weights&Biases) 是轻量级的在线模型训练可视化工具,类似于 TensorBoard,可以帮助用户跟踪…...

N1922A是德科技N1922A功率传感器
181/2461/8938产品概述: N192XA 传感器是首款通过将直流参考源和开关电路集成到功率传感器中来提供内部调零和校准的传感器。此功能消除了与使用外部校准源相关的多个连接,从而最大限度地减少了连接器磨损、测试时间和测量不确定性。 连接到 DUT 时进行…...

最简洁的Docker环境配置
Docker环境配置 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Mac、Linux或Windows操作系统的机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不…...
Docker内更新Jenkins详细讲解
很多小伙伴在Docker中使用Jenkins时更新遇到困难,本次结合自己的实际经验,详细讲解。根据官网Jenkins了解以下内容: 一、Jenkins 是什么? Jenkins是一款开源 CI&CD 软件,用于自动化各种任务,包括构建、测…...

基于遗传模拟退火混合优化算法的车间作业最优调度matlab仿真,输出甘特图
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 4.1遗传算法与模拟退火算法简介 4.2 GSAHO算法应用于JSSP 5.完整程序 1.程序功能描述 车间作业调度问题(Job Shop Scheduling Problem, JSSP)是一种典型的生产调度问…...

Mac 安装 brew brew cask 遇到的问题以及解决办法
安装Homebrew和Homebrew Cask是在Mac上管理软件包的常用方法。虽然大多数情况下安装这两个工具是比较简单的,但有时候也可能遇到一些问题。下面是一些常见的问题以及解决办法: 问题1:无法安装Homebrew 解决办法: 1.确保你的Mac已连…...

Vitalik Buterin香港主旨演讲:协议过去10年迅速发展,但存在效率、安全两大问题
2024 香港 Web3 嘉年华期间,以太坊联合创始人 Vitalik Buterin 在由DRK Lab主办的“Web3 学者峰会 2024”上发表主旨演讲《Reaching the Limits of Protocol Design》。 他介绍到,2010年代,基于基本密码学的协议是哈希、签名。随后ÿ…...

【leetcode】大数相加
题目链接:415. 字符串相加 - 力扣(LeetCode) 计算两个大数的和,从末尾开始逐个字符相加,记录进位 class Solution { public:string addStrings(string num1, string num2) {int i num1.size() - 1, j num2.size() …...

数据检索的优化之道:B树与B+树的深度解析与应用探索
1、引言 在信息时代,数据检索的速度和效率对于任何依赖数据处理的系统来说都至关重要。无论是在线搜索引擎、数据库管理系统还是文件存储系统,快速准确地检索所需数据都是核心需求。传统的线性数据结构在处理大规模数据集时往往力不从心,因此…...

替换服务器的SSL证书有什么影响?
SSL证书是保护网站和用户数据安全的重要组成部分。然而,出于一些原因,网站管理员可能需要替换服务器的SSL证书。替换SSL证书可能会对网站的运行和安全产生一些影响。本文旨在介绍替换服务器SSL证书的影响和相关注意事项,帮助网站管理员更好地…...

java中可变参数和简单游戏
可变参数: 就是一种特殊形参,定义在方法,构造器的形参列表中,格式是:数据类型...参数名称 可变参数的好处: 灵活的接收数据 特点:可以不传数据给它,可以传一个数据或者多个数据给它…...

软考高级架构师:TCP/IP 协议 和 OSI 七层模型
一、AI 讲解 TCP/IP 协议族是一组计算机网络通信协议的集合,其中TCP和IP是两个核心协议。TCP/IP 协议族通常被用来参照互联网的基础通信架构。与之相对的OSI七层模型,是一个更为理论化的网络通信模型,它将网络通信分为七个层次。 TCP/IP 与…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
