python项目练习——19、单词计数器
这个项目允许用户输入一段文本,然后统计其中每个单词出现的次数,并按照出现次数从高到低进行排序显示。它涉及到字符串处理、数据结构和用户界面设计等方面的技术。
示例:
import tkinter as tk # 导入 Tkinter 库
from collections import Counter # 导入计数器工具类class WordCounterApp:
def __init__(self, master):
self.master = master
self.master.title('单词计数器')# 创建界面组件
self.label_text = tk.Label(master, text='输入文本:')
self.label_text.grid(row=0, column=0)
self.entry_text = tk.Entry(master, width=50)
self.entry_text.grid(row=0, column=1)self.btn_count = tk.Button(master, text='统计单词', command=self.count_words)
self.btn_count.grid(row=1, column=0, columnspan=2)self.text_output = tk.Text(master, width=60, height=10)
self.text_output.grid(row=2, column&
相关文章:

python项目练习——19、单词计数器
这个项目允许用户输入一段文本,然后统计其中每个单词出现的次数,并按照出现次数从高到低进行排序显示。它涉及到字符串处理、数据结构和用户界面设计等方面的技术。 示例: import tkinter as tk # 导入 Tkinter 库 from collections import Counter # 导入计数器工具类 c…...
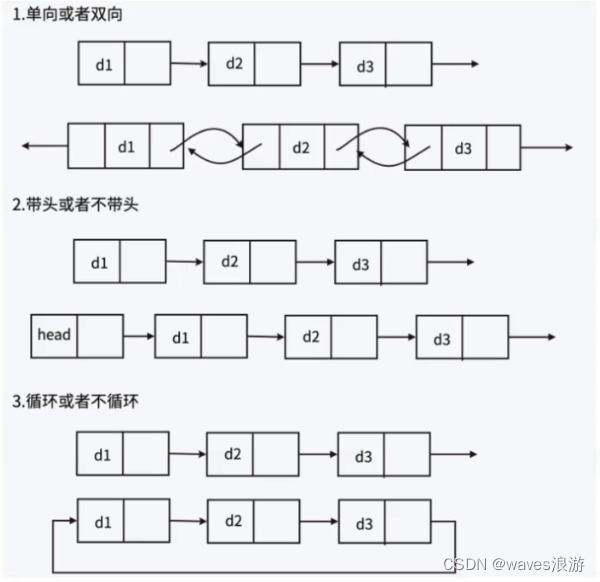
单链表专题
文章目录 目录1. 链表的概念及结构2. 实现单链表2.1 链表的打印2.2 链表的尾插2.3 链表的头插2.4 链表的尾删2.5 链表的头删2.6 查找2.7 在指定位置之前插入数据2.8 在指定位置之后插入数据2.9 删除pos节点2.10 删除pos之后的节点2.11 销毁链表 3. 链表的分类 目录 链表的概念…...

js把数组中的某一项移动到第一位
在JavaScript中,如果你要将数组中的某一项移动到第一位,你可以使用以下几种方法。 假设我们有一个数组arr,并且想要将位于索引index的项移动到数组的第一个位置: let arr [1, 2, 3, 4, 5]; let index 2; // 假设我们想将3&…...

MyBatis如何实现分页
文章目录 MyBatis分页方式对比使用数据库厂商提供的分页查询语句通过自定义 SQL 实现分页逻辑1. 使用 RowBounds 实现分页2. 使用 PageHelper 实现分页 数组分页使用 MyBatis-Plus 进行分页MyBatis物理分页和逻辑分页MyBatis 手写一个 拦截器分页 在 MyBatis 中实现分页通常有两…...

在 Python 编程中,面向对象编程的核心概念包括哪些部分?
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 在 Python 编程中,面向对象编程(Object-Oriented Programming,OOP)的核心概念主要包括类(Class)、对象(Object&#x…...

elementui树形组件自定义高亮颜色
1、需求描述:点击按钮切换树形的章节,同时高亮 2、代码实现 1)style样式添加 <style> .el-tree--highlight-current .el-tree-node.is-current > .el-tree-node__content {background-color: #81d3f8 !important; //高亮颜色colo…...

富格林:技巧抵抗曝光虚假套路
富格林悉知,黄金具备独特的优势吸引着众多投资者的目光,在现货黄金市场也被认为是一条潜力无限的盈利之道。但我们要明白风险与盈利是相辅相成的,因此在这复杂的市场中我们必须利用技巧来抵抗曝光的虚假套路。下面富格林将给大家分享一些正确…...
24年权威数学建模报名通知汇总(含妈妈杯、国赛、美赛、电工杯、数维杯、五一数模、深圳杯......)
1、MathorCup比赛 报名时间:2024年4月11日中午12点(周四) 比赛开始时间:2024年4月12日上午8时(周五) 比赛结束时间:2024年4月16日上午9时(周二) 报名费用:…...
【C语言自定义类型之----结构体,联合体和枚举】
一.结构体 1.结构体类型的声明 srruct tag {nemer-list;//成员列表 }varible-list;//变量列表结构体在声明的时候,可以不完全声明。 例如:描述一个学生 struct stu {char name[20];//名字int age;//年龄char sex[20];//性别 };//分号不能省略2.结构体…...
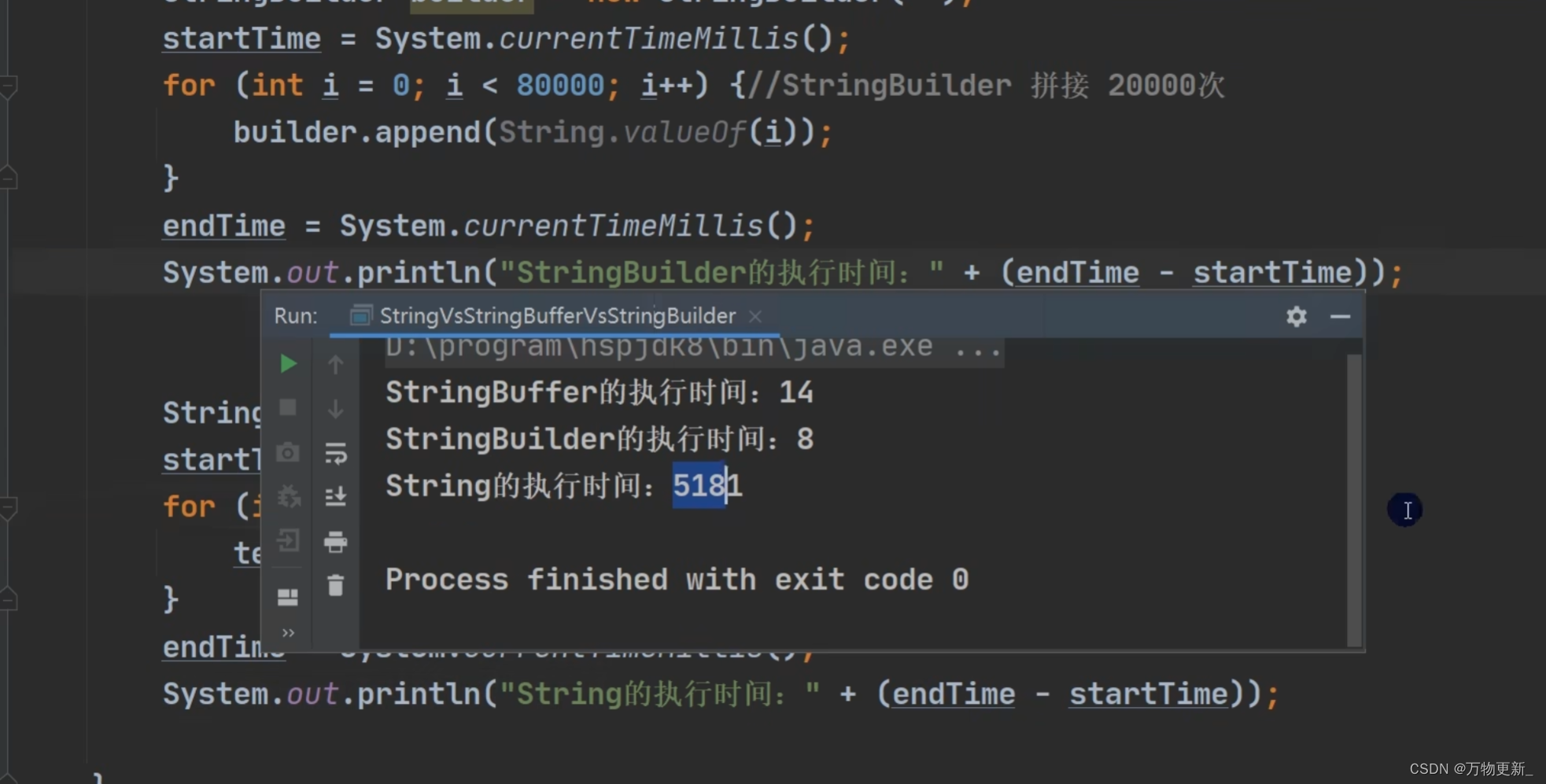
[Java基础揉碎]StringBuffer类 StringBuild类
目录 StringBuffer类 介绍 继承图 String VS StringBuffer StringBuffer的构造器 String和StringBuffer的转换 StringBuffer类常见方法 测试题 StringBuild类 基本介绍 继承图 String、StringBuffer 和StringBuilder的比较 通过字符串拼接循环测试可以看到各自的性…...
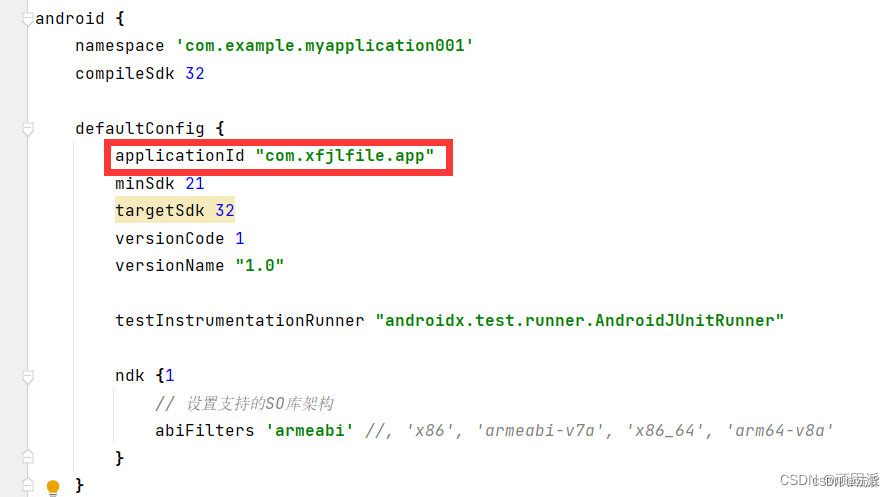
Android Studio修改项目包名
1.第一步,项目结构是这样的,3个包名合在了一起,我们需要把每个包名单独展示出来 2.我们点击这个 取消选中后的包名结构是这样的,可以看到,包名的每个文件夹已经展示分开了,现在我们可以单独对每个包名文件夹…...

c++语言增强的地方
目录 1.对全局变量的检测能力 2.struct类型增强 3.c中所有变量和函数都必须有类型 4.c中新增的bool类型 5.三目运算符的加强 6.const的增强 7.对枚举的增强 1.对全局变量的检测能力 C语言中同时定义两个相同的全局变量编译器并不会报错,而c中就会报重定义错…...

评论发布完整篇(react版)
此篇文章阐述评论的最新、最热之间的tab标签切换(包括当前所在tab标签的高亮显示问题);当前评论的删除;除此之外还延伸了用户的评论实时发布功能。其中最新tab标签所展示的内容是根据当前评论点赞数来进行排序,点赞数量…...

前端window.open的简单使用
JavaScript 中的 Window.open() 用法详解-CSDN博客 window.open("https://www.baidu.com/?tn49055317_12_hao_pg", _blank);...

基于开源软件构建存储解决方案的思考
近来看了一些IBM的存储产品的资料,有一些收获。 依据存储软件和搭配硬件,IBM存储产品的组合,大致分类如下: 自研存储软件,搭配自研专有硬件自研存储软件,搭配通用服务器硬件,比如IBM Storage S…...

【leetcode】动态规划::前缀和(二)
标题:【leetcode】前缀和(二) 水墨不写bug 正文开始: (一) 和为K的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续…...

SpringBoot自动装配原理之@Import注解解析
文章目录 1. 概述2. 使用2.1 导入普通Bean2.2 导入配置类2.3 导入 ImportSelector 实现类2.4 导入 ImportBeanDefinitionRegistrar 实现类 3. 区别 1. 概述 当谈及现代Java开发领域中的框架选择时,SpringBoot无疑是无与伦比的热门之选。其简化了开发流程࿰…...
49 样式迁移【李沐动手学深度学习v2课程笔记】
1. 样式迁移(Style Transfer) 计算机视觉的应用之一,将样式图片中的样式(比如油画风格等)迁移到内容图片(比如实拍的图片)上,得到合成图片 可以理解成为一个滤镜,但相对于滤镜来讲…...

Linux的学习之路:4、权限
一、Linux权限的概念 权限我们都熟悉,最常见的就是在看电视时需要vip这个就是权限,然后在Linux就是有两个权限,就是管理员也就是超级用户和普通的用户 命令:su [用户名] 功能:切换用户。 例如,要从root用户…...

自定义类型—结构体
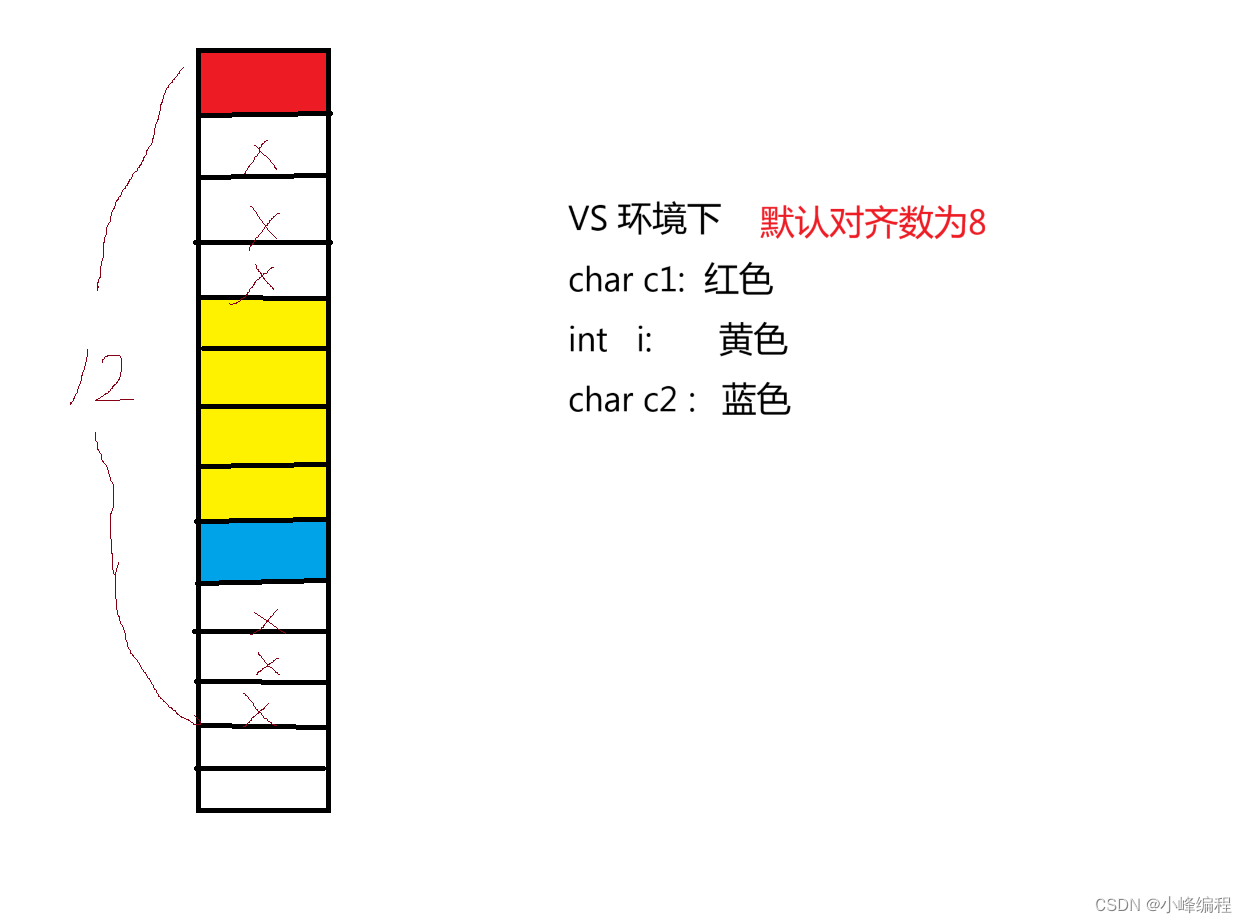
目录 1 . 结构体类型的声明 1.1 结构的声明 1.2 结构体变量的创建与初始化 1.3 结构体的特殊声明 1.4 结构体的自引用 2. 结构体内存对齐 2.1 对齐规则 2.2 为什么存在内存对齐 2.3 修改默认对齐数 3. 结构体传参 4.结构体实现位段 4.1 位段的内存分配 4.3 位段的…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
