倒立摆建模
前言
系统由一辆具有动力的小车和安装在小车上的倒立摆组成,系统是不稳定,我们需要通过控制移动小车使得倒立摆保持平衡。
具体地,考虑二维情形如下图,控制力为水平力FFF,输出为角度θ\thetaθ以及小车的位置xxx。
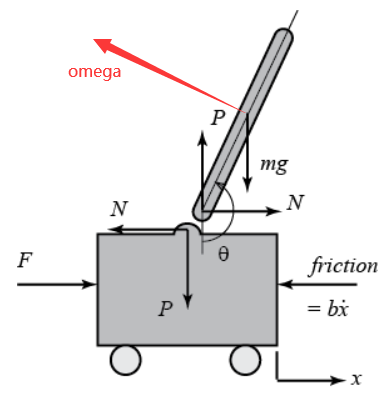
力分析和系统方程
设两个物体在水平和竖直方向上的相互作用力分别为NNN和PPP。
将小车水平方向上的力相加,得到牛顿力学方程:
Mx¨+bx˙+N=FM\ddot{x}+b\dot{x}+N=FMx¨+bx˙+N=F
将倒立摆水平方向上的力相加,得到:
N=mx¨+mlθ¨cosθ−mlθ˙2sinθN=m\ddot{x}+ml\ddot{\theta}cos\theta-ml\dot{\theta}^2sin\thetaN=mx¨+mlθ¨cosθ−mlθ˙2sinθ
将NNN消去,得
Mx¨+bx˙+mx¨+mlθ¨cosθ−mlθ˙2sinθ=FM\ddot{x}+b\dot{x}+m\ddot{x}+ml\ddot{\theta}cos\theta-ml\dot{\theta}^2sin\theta=FMx¨+bx˙+mx¨+mlθ¨cosθ−mlθ˙2sinθ=F
将垂直于摆的力相加,得
Psinθ+Ncosθ−mgsinθ=mlθ¨+mx¨cosθ(a)Psin\theta+Ncos\theta-mgsin\theta=ml\ddot{\theta}+m\ddot{x}cos\theta(a)Psinθ+Ncosθ−mgsinθ=mlθ¨+mx¨cosθ(a)
为了消去P,NP,NP,N两项,将两个物体质心的力矩相加,得
Plsinθ−Nlcosθ=Iθ¨(b)Plsin\theta-Nlcos\theta=I\ddot{\theta}(b)Plsinθ−Nlcosθ=Iθ¨(b)
(a)×l+(b)(a)\times l+(b)(a)×l+(b)得
(I+ml2)θ¨+mglsinθ=−mlx¨cosθ(I+ml^2)\ddot{\theta}+mglsin\theta=-ml\ddot{x}cos\theta(I+ml2)θ¨+mglsinθ=−mlx¨cosθ
线性化
将上述方程线性化,θ=π\theta=\piθ=π,并假设系统保持在这个平衡的小邻域内。设ϕ\phiϕ为摆对平衡位置的偏差,满足θ=π+ϕ\theta=\pi+\phiθ=π+ϕ,若偏差十分小,使用以下近似:
cosθ=cos(π+ϕ)≈−1sinθ=sin(π+ϕ)≈−ϕθ¨2=ϕ˙2≈0cos\theta=cos(\pi+\phi)\approx-1 \\ sin\theta=sin(\pi+\phi)\approx-\phi \\ \ddot{\theta}^2=\dot{\phi}^2\approx0cosθ=cos(π+ϕ)≈−1sinθ=sin(π+ϕ)≈−ϕθ¨2=ϕ˙2≈0
将上述近似公式应用至前面的非线性控制方程,得到两个线性化的方程,并使用uuu替代FFF得
(I+ml2)ϕ¨−mglϕ=mlx¨(M+m)x¨+bx˙−mlϕ¨=u(I+ml^2)\ddot{\phi}-mgl\phi=ml\ddot{x} \\ (M+m)\ddot{x}+b\dot{x}-ml\ddot{\phi}=u(I+ml2)ϕ¨−mglϕ=mlx¨(M+m)x¨+bx˙−mlϕ¨=u
传递函数
假设初始条件为0,对系统方程应用拉普拉斯变换:
todo
相关文章:

倒立摆建模
前言 系统由一辆具有动力的小车和安装在小车上的倒立摆组成,系统是不稳定,我们需要通过控制移动小车使得倒立摆保持平衡。 具体地,考虑二维情形如下图,控制力为水平力FFF,输出为角度θ\thetaθ以及小车的位置xxx。 力…...

SpringSecurity支持WebAuthn认证
WebAuthn是无密码身份验证技术,解决了密码泄露的风险,主流的浏览器都支持。有很多开源的类库实现了WebAuthn规范,Java下流行的类库有:webauthn4jjava-webauthn-serververtx-authSpring Security官方暂时未支持WebAuthn,…...
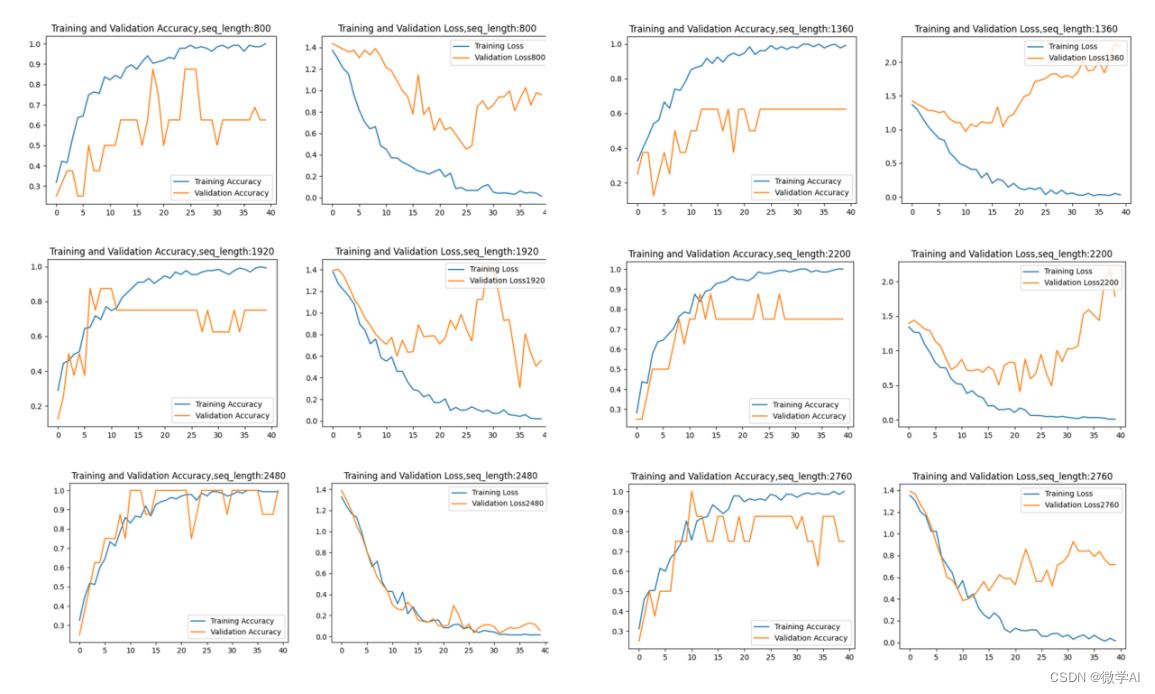
深度学习技巧应用3-神经网络中的超参数搜索
大家好,我是微学AI,今天给大家带来深度学习技巧应用3-神经网络中的超参数搜索。 在深度学习任务中,一个算法模型的性能往往受到很多超参数的影响。超参数是指在模型训练之前需要我们手动设定的参数,例如:学习率、正则…...
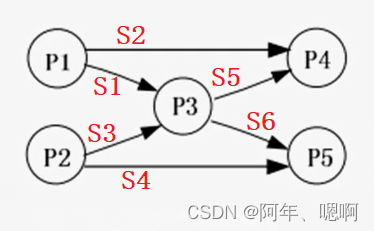
【信号量机制及应用】
水善利万物而不争,处众人之所恶,故几于道💦 目录 一、信号量机制 二、信号量的应用 >利用信号量实现进程互斥 >利用信号量实现前驱关系 >利用记录型信号量实现同步 三、例题 四、参考 一、信号量机制 信号量是操作系统提…...

围棋高手郭广昌的“假眼”棋局
(图片来源于网络,侵删)文丨熔财经作者|易不二2022年,在复星深陷债务压顶和变卖资产漩涡的而立之年,“消失”已久的郭广昌,在质疑与非议声中回国稳定军心,强调复星将在未来的五到十年迎来一个全新…...

学成教育-统一异常处理实现
一、统一异常处理实现 统一在base基础工程实现统一异常处理,各模块依赖了base基础工程都 可以使用。 首先在base基础工程添加需要依赖的包: <dependency><groupId>org.springframework</groupId><artifactId>spring-web</…...
JNI内通过参数形式从C/C++中传递string类型数据至Java层
目录 0 前言 1 string类型参数形式传值 2 测试和结果 0 前言 类似之前我写过的两篇文章:一篇介绍了在JNI中基础类型int的传值方式;一篇详细梳理了在JNI层中多维数组的多种传值方式。 JNI内两种方式从C/C中传递一维、二维、三维数组数据至Java层详细…...
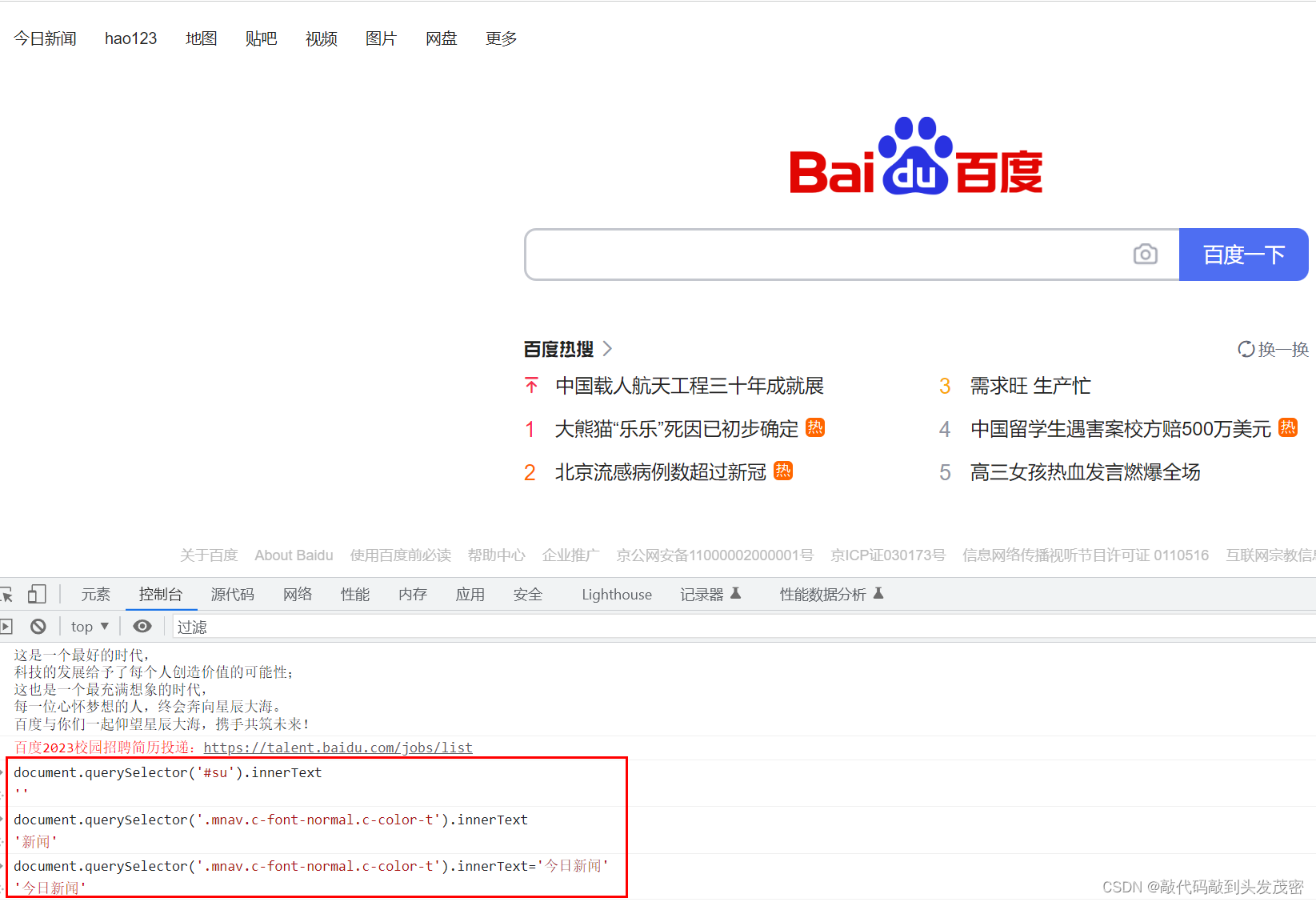
自动化测试——执行javaScript脚本
文章目录一、点击元素(对应的click())二、input标签对应的值(对应的send_keys())修改时间控件的属性值:三、元素的文本属性四、js脚本滚动操作一、点击元素(对应的click()) 使用场景:当使用显性等待不能解决问题时 代码中实现点击…...

常用十种算法滤波
十种算法滤波1. 限幅滤波法(又称程序判断滤波法)2. 中位值滤波法3. 算术平均滤波法4. 递推平均滤波法(又称滑动平均滤波法)5. 中位值平均滤波法(又称防脉冲干扰平均滤波法)6. 限幅平均滤波法7. 一阶滞后滤波…...

IO多路复用
一、概述 IO多路复用:进程同时检查多个文件描述符,以找出他们中的任何一个是否可执行IO操作。 核心:同时检查多个文件描述符,看他们是否准备好了执行IO操作。文件描述符就绪状态的转化是通过一些IO事件来触发。 二、水平触发和…...

Python中的错误是什么,Python中有哪些错误
7.1 错误(errors) 由于Python代码通常是人类编写的,那么无论代码是在解释之前还是运行之后,或多或少总会出现一些问题。 在Python代码解释时遇到的问题称为错误,通常是语法和缩进问题导致的,这些错误会导致代码无法通过解释器的解…...
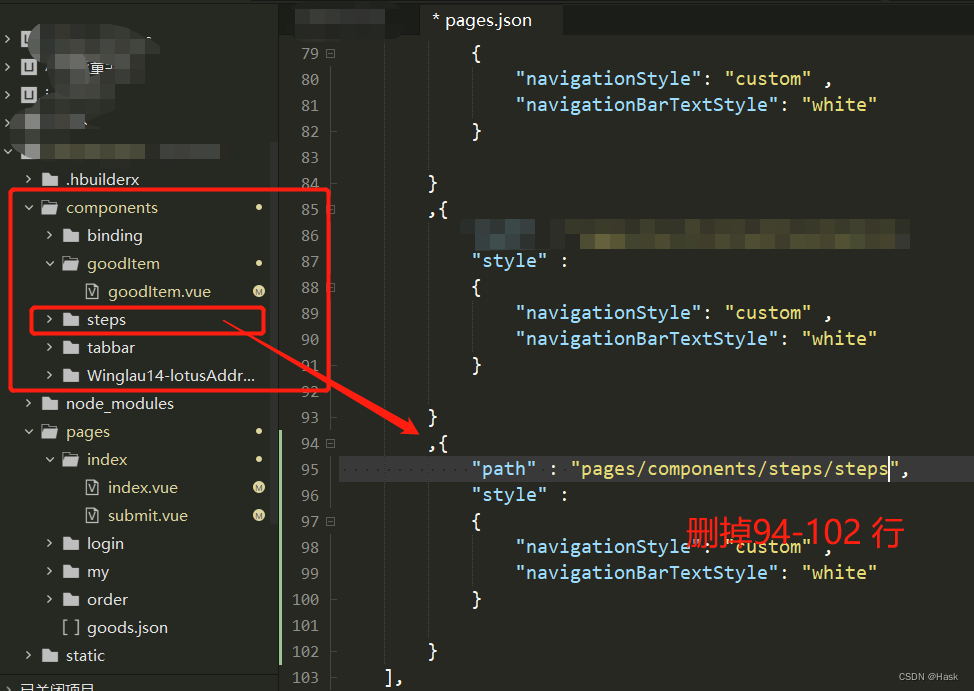
记录自己开发一款小程序中所遇到的问题(uniapp+uview)(持续更新)
每次开发小程序中,都会遇到各种各样的问题。但是有的问题已经遇到过了,但是遇到的时候还是要各种的问度娘。 特此出这篇文章,方便自己也是方便大家。 仅供参考 1. u-collapse的样式在h5中正常,但是运行到微信小程序中样式就乱了…...

华为机试 HJ43 迷宫问题
经典迷宫问题dfs 题目链接 描述 定义一个二维数组 N*M ,如 5 5 数组下所示: int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫,其中的1表示墙壁,0表示可以走…...
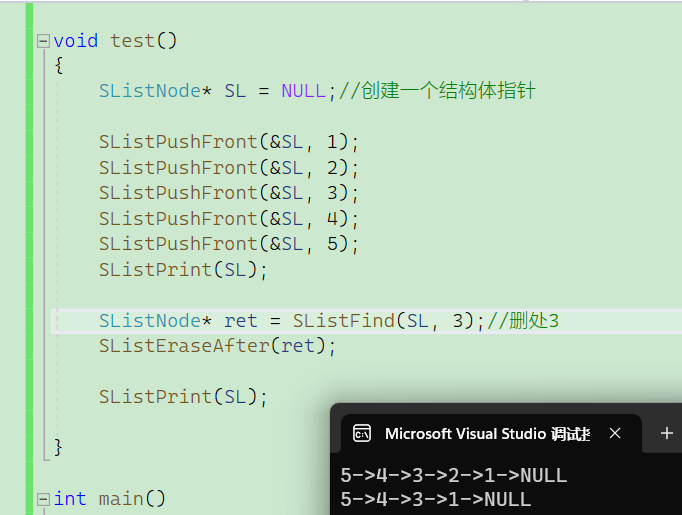
数据结构|链表
概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。单链表的形式就像一条铁链环环相扣它与顺序表最大的不同是,单链表的数据存储是在不连续的空间,存储的数据里面含有…...

计算机写论文时,怎么引用文献? - 易智编译EaseEditing
首先需要清楚哪些引用必须注明[1]: 任何直接引用都要用引号并注明来源; 任何不是自己的口头或书面的观点、解释和结论都应注明来源; 即使不用原话,但是他人的思路、概念或观点也应注明; 不要为了适合你的观点修改原…...

实验三:贪心
1.减肥的小k1 题目描述 小K没事干,他要搬砖头,为了达到较好的减肥效果,教练规定的方式很特别: 每一次,小K可以把两堆砖头合并到一起,消耗的体力等于两堆砖头的重量之和。 经过 n-1次合并后, …...
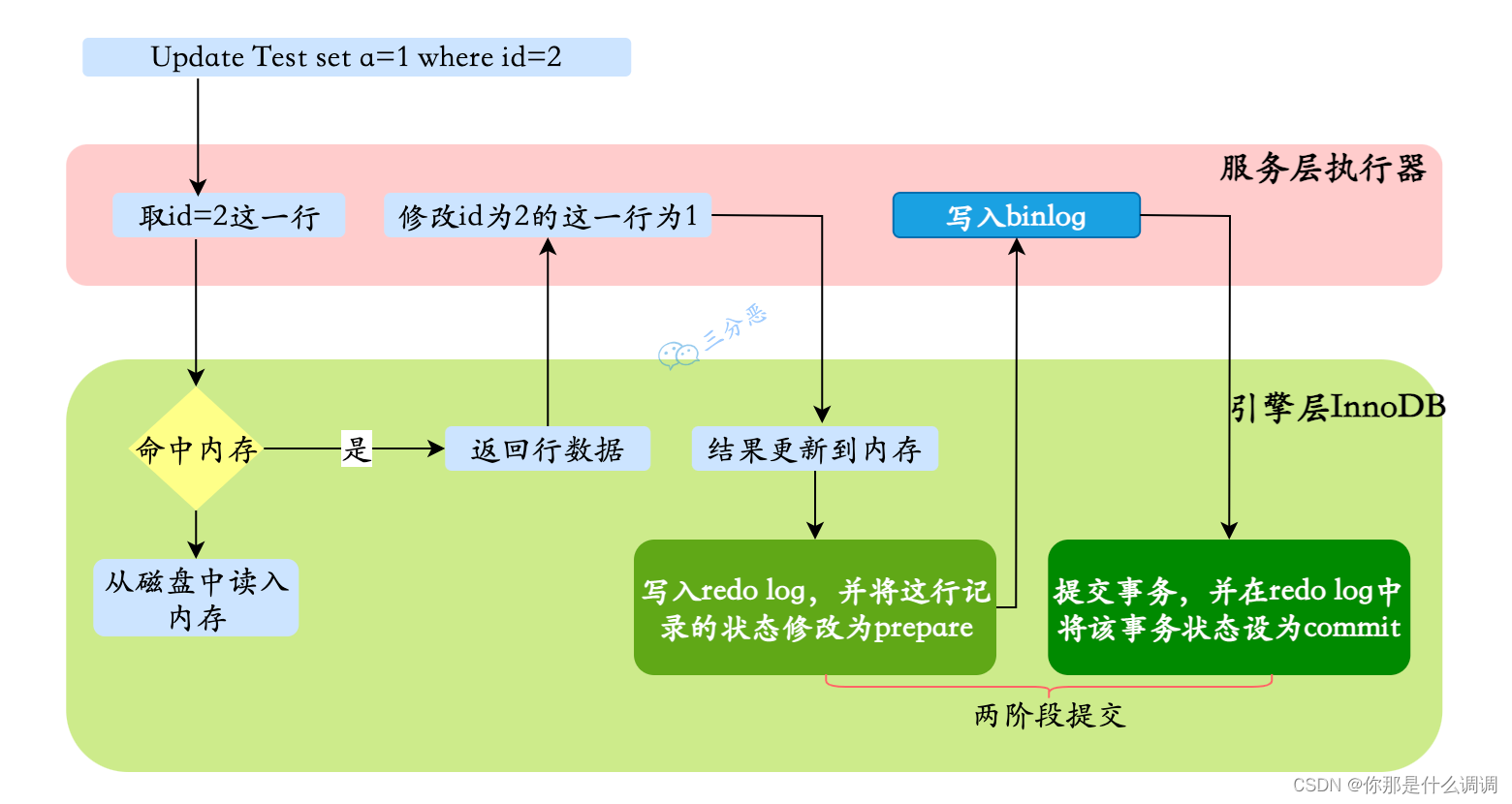
MySQL日志文件
文章目录1.MySQL中的日志文件2.bin log的作用3.redo log的作用4.bin log和redo log的区别(1)存储的内容(2)功能(3)写入时间(4)写入方式5.两阶段提交6.undo log的作用1.MySQL中的日志…...

Intel8086处理器使用NASM汇编语言实现操作系统08-关于负数的相关处理idiv/cbw/cwde/cdqu/cwd/cdq/cdo/
很多人都知道一个有符号的数,最高位是1,则表示负数,最高位是0,则表示正数,如果假设我的CPU是4位CPU,那么对于1001这个数,是表示9,还是表示-7呢???…...
JavaScript 混淆技术
根据JShaman(JShaman是专业的JavaScript代码混淆加密网站)提供的消息,JavaScript混淆技术大体有以下几种: 变量混淆 将带有JS代码的变量名、方法名、常量名随机变为无意义的类乱码字符串,降低代码可读性,如…...

安装库报错:No CUDA runtime is found, using CUDA_HOME=‘/usr/local/cuda-11.3‘
1、报错内容 安装库时报错: No CUDA runtime is found, using CUDA_HOME/usr/local/cuda-11.32、检查 查看cuda版本和pytorch版本 python 进入python环境 import torch torch.__version__ torch.cuda.is_available()nvidia-smi 因此发现是由于该虚拟环境中CUDA与…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
