AI助力M-OFDFT实现兼具精度与效率的电子结构方法
编者按:为了使电子结构方法突破当前广泛应用的密度泛函理论(KSDFT)所能求解的分子体系规模,微软研究院科学智能中心的研究员们基于人工智能技术和无轨道密度泛函理论(OFDFT)开发了一种新的电子结构计算框架 M-OFDFT。这一框架不仅保持了与 KSDFT 相当的计算精度,而且在计算效率上实现了显著提升,并展现了优异的外推性能,为分子科学研究中诸多计算方法的基础——电子结构方法开辟了新的思路。相关研究成果已在国际知名学术期刊《自然-计算科学》(Nature Computational Science)上发表。
近几十年来,理论与计算化学领域取得的一大成就是能够通过计算手段得到分子体系的物理化学性质。这为药物发现和材料设计等诸多工业界问题带来了全新的研究手段,有望缩短开发流程并降低开发成本。这些计算方法的基础步骤是使用电子结构方法求解给定分子体系的电子状态,进而得到该体系的各种性质。
然而,各种电子结构方法的求解精度和计算效率往往无法兼得。当前,取得相对合理的“精度-效率”权衡而被广泛应用的方法是 Kohn-Sham 形式的密度泛函理论(Kohn-Sham density functional theory, KSDFT)。但 KSDFT 具有较高的计算复杂度,不能很好地满足日益增长的求解大规模分子体系的需求。为此,微软研究院科学智能中心的研究员们提出了一种基于深度学习和无轨道密度泛函理论(OFDFT)的电子结构计算框架 M-OFDFT,其不仅显著超越了 KSDFT 的计算效率,还能保有其求解精度。这一成果展示了人工智能在提升电子结构计算中“精度-效率”权衡方面的卓越能力,并将助力加速相关业界问题的研究与开发。M-OFDFT 的相关研究成果已在国际知名学术期刊《自然-计算科学》(Nature Computational Science)上发表。

M-OFDFT 相关研究已发表在《自然-计算科学》(Nature Computational Science)上
Overcoming the Barrier of Orbital-Free Density Functional Theory for Molecular Systems Using Deep Learning
《自然-计算科学》文章链接:https://www.nature.com/articles/s43588-024-00605-8
SharedIt 链接:https://rdcu.be/dANtS
论文链接:https://arxiv.org/abs/2309.16578
人工智能给电子结构方法带来新机会
电子结构方法是求解分子体系各种物理化学性质的基础工具。由于多电子体系本身具有一定的求解难度,所以高精度电子结构方法因其较高的计算代价很难应用到工业界所关注的分子体系中,而可计算较大分子的方法则会因引入一些近似而损失精度。目前 KSDFT 因其相对合适的精度与效率权衡得到了广泛应用。
不过,近期人工智能技术的喜人进展也为其他电子结构计算框架带来了新的机会。为了使电子结构方法突破 KSDFT 所能求解的分子体系规模,微软研究院的研究员们利用人工智能技术,开发了 M-OFDFT,该方法比 KSDFT 效率更高,同时又能保有其精度。基于 OFDFT 的开发,让 M-OFDFT 成为了一种比 KSDFT 理论复杂度更低的电子结构计算框架,因为它只需优化电子密度函数 ρ(r) 这一个函数来求解电子状态即可,KSDFT 则需要优化与电子数相同的多个函数。
不过,OFDFT 面临着一个巨大的挑战——需要电子动能关于密度函数的泛函 T_S [ρ],但它的形式未知,并且难以构造适用于分子体系的高精度近似。
针对这一难题,M-OFDFT 使用一个深度学习模型 T_(S,θ) 来近似动能泛函。借助深度学习模型的强大拟合能力,M-OFDFT 可实现比基于近似物理模型设计的经典动能泛函更高的准确度。对于一个待求解的分子体系结构,M-OFDFT 会使用动能泛函模型 T_(S,θ) 以及其他可直接计算的能量项构造出一个电子密度的优化目标,然后通过优化过程求解最优(基态)电子密度(图1),进而可计算能量、力、电荷分布等分子属性。

图1:对于待求解的分子体系结构 M,M-OFDFT 通过最小化电子能量 E_θ 来求解电子密度(以其向量化系数 p 表示),其中难以近似的动能部分由深度学习模型 T_(S,θ) 来近似
M-OFDFT实现兼具精度与效率的电子结构方法
研究员们对 M-OFDFT 进行了一系列的实验验证。首先考察的是 M-OFDFT 在常见小分子体系上的求解精度。结果显示,M-OFDFT 在乙醇分子构象以及 QM9 数据集的分子上可以达到与KSDFT相当的精度(能量达到化学精度1 kcal/mol)。相较于经典 OFDFT 方法,精度提高了两个数量级(图2-a)。M-OFDFT 解得的电子密度也与 KSDFT 的结果重合(图2-b),特别是得到了电子壳层结构,而经典 OFDFT 的结果则有明显偏差。由 M-OFDFT 解得的乙醇构象空间上的势能面(每个点都是通过密度优化得到的,并不是直接预测)也与 KSDFT 的结果一致(图2-c)。

图2:M-OFDFT 和一些经典 OFDFT 在分子体系上与 KSDFT 的比较
之后,研究员们又验证了 M-OFDFT 不仅保有 KSDFT 级别的精度,其更低的理论计算复杂度还使其在效率上也超越了 KSDFT。在实际计算中 M-OFDFT 取得了 O(N^1.46) 的复杂度(图3),比 KSDFT 的实际复杂度 O(N^2.49) 低了一阶,且其所需绝对时间也明显少于 KSDFT。在两个更大的蛋白质体系上(包含2676和2750个电子),M-OFDFT 实现了25.6倍和27.4倍的加速。
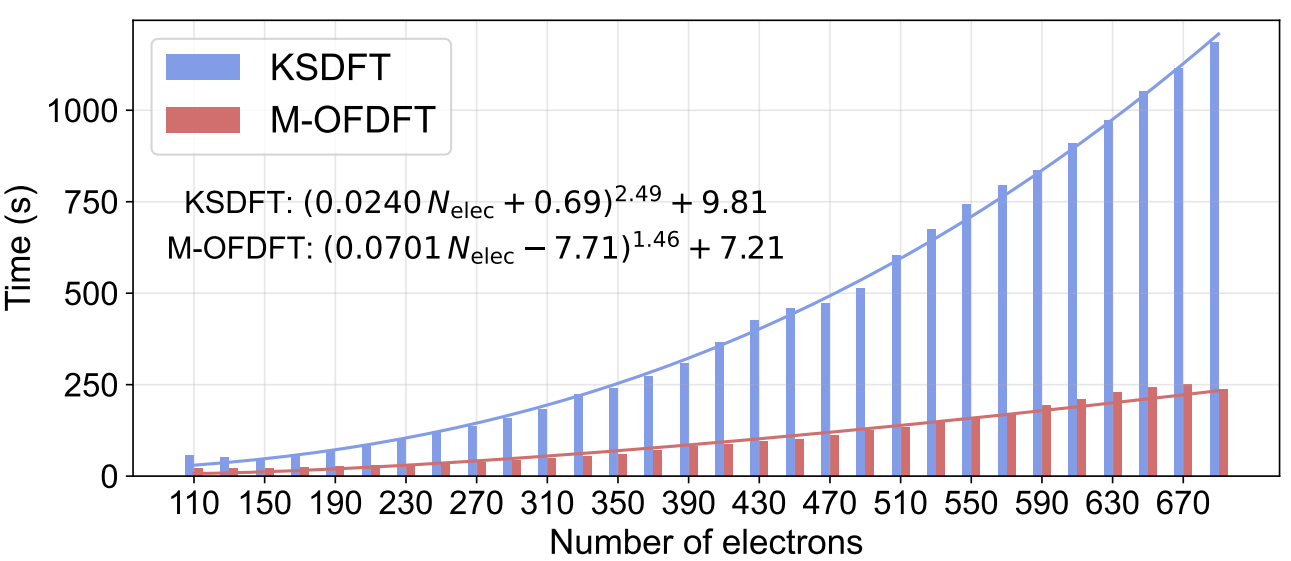
图3:M-OFDFT 和 KSDFT 的实际计算时间及复杂度
M-OFDFT具有更强的泛化能力
深度学习模型在科学任务中的应用面临一大挑战是,在具有与训练数据不同特点的数据上的泛化问题。但采用了 OFDFT 框架后,动能泛函模型遇到的泛化问题就会减轻,从而使 M-OFDFT 可以在比训练集分子规模更大的体系上展现出良好的外推能力。
实验结果表明,M-OFDFT 的能量预测误差显著低于基于深度学习的端到端能量预测模型(图4-a)。此外,研究员们还利用在多肽片段上训练的 M-OFDFT 模型求解完整蛋白结构,并取得了超越端到端模型和经典 OFDFT 的泛化性能(图4-c)。不仅如此,相较端到端模型,M-OFDFT 还可以用更少的大分子体系训练数据取得更好的泛化表现(图4-b与图4-d)。
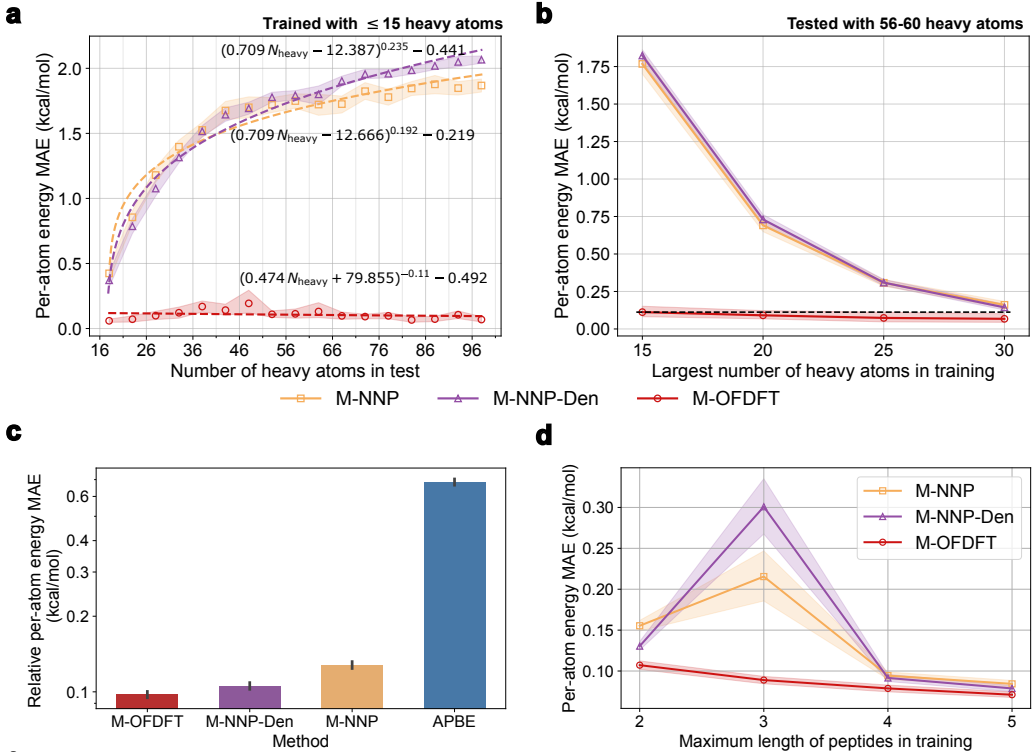
图4:M-OFDFT 和其他深度学习方法的泛化性能比较
M-OFDFT的工作原理
“神龙见首又见尾”:高效捕获非局域效应的动能泛函模型
动能密度泛函具有明显的非局域效应,而用经典的基于格点(grid)的方式表征电子密度则会带来高昂的非局域计算代价。为此,M-OFDFT 将电子密度在一组原子基组函数上展开,并使用展开系数 p 作为电子密度表征。由于基函数叠加的形状与电子分布接近,所以其数量可远小于格点数,使得非局域计算代价大大降低,并有助于刻画电子密度中的壳层结构。
M-OFDFT 将每个原子上的电子密度系数 p 和类型 Z 与坐标 x 作为节点特征,并基于 Graphormer 模型[1]预测电子动能 T_(S,θ)(图5),其自注意力机制显式刻画了荷载在每两个原子上的电子密度特征之间的相互作用,从而可捕捉非局域性质。此外,为了保证动能的旋转不变性,M-OFDFT 使用了以各个原子为中心、基于其相邻原子的局部坐标系,将电子密度系数转换为旋转不变的特征。

图5:基于非局域图神经网络的动能密度泛函模型
“横看成岭侧成峰,远近高低各不同”:高效学习电子能量曲面的训练策略
与传统机器学习任务不同,动能泛函模型是被当作其输入变量的优化目标使用的,而非用于在一些单点上做预测,这对模型的学习提出了更高的要求:模型必须捕捉到每个分子结构上电子能量曲面的轮廓。
为此,研究员们深入分析了用来生成数据的电子结构方法,发现它其实可以为每个分子结构生成多个数据点,而且还能提供梯度标注,从而让模型可以拥有更丰富的曲面轮廓特征。然而梯度的巨大范围也使神经网络难以优化。对此,研究员们还提出了一系列增强模块,让模型能够更容易地表达巨大的梯度。
开启未来电子结构方法的新篇章
M-OFDFT 成功突破了无轨道密度泛函框架在分子体系中的瓶颈,将其求解精度提升到了常用的 KSDFT 的水平,同时保有了其更低的计算代价,推进了电子结构方法在“精度-效率”方面的权衡,为分子科学研究提供了一种更有潜力的研究工具。
尽管 M-OFDFT 已经在某些分子体系上展现了出色的泛化性能,但在更大的分子体系上实现长时间且稳定的高精度模拟仍是一个巨大的挑战。微软研究院期待 M-OFDFT 可以沿着这一方向激发更多研究与创新,并在未来和其他方法一起为电子结构计算带来更多突破性的成果和影响。
相关文章
[1] Do Transformers really perform badly for graph representation? Advances in Neural Information Processing Systems 34 (NeurIPS 2021)
https://proceedings.neurips.cc/paper/2021/hash/f1c1592588411002af340cbaedd6fc33-Abstract.html
相关文章:

AI助力M-OFDFT实现兼具精度与效率的电子结构方法
编者按:为了使电子结构方法突破当前广泛应用的密度泛函理论(KSDFT)所能求解的分子体系规模,微软研究院科学智能中心的研究员们基于人工智能技术和无轨道密度泛函理论(OFDFT)开发了一种新的电子结构计算框架…...
【数据结构】单链表(一)
上一篇【数据结构】顺序表-CSDN博客 我们了解了顺序表,但是呢顺序表涉及到了一些问题,比如,中间/头部的插入/删除,时间复杂度为O(N);增容申请空间、拷贝、释放旧空间会有不小的消耗;增容所浪费的空间... 我们如何去解…...

SCI一区 | Matlab实现INFO-TCN-BiGRU-Attention向量加权算法优化时间卷积双向门控循环单元注意力机制多变量时间序列预测
SCI一区 | Matlab实现INFO-TCN-BiGRU-Attention向量加权算法优化时间卷积双向门控循环单元注意力机制多变量时间序列预测 目录 SCI一区 | Matlab实现INFO-TCN-BiGRU-Attention向量加权算法优化时间卷积双向门控循环单元注意力机制多变量时间序列预测预测效果基本介绍模型描述程…...
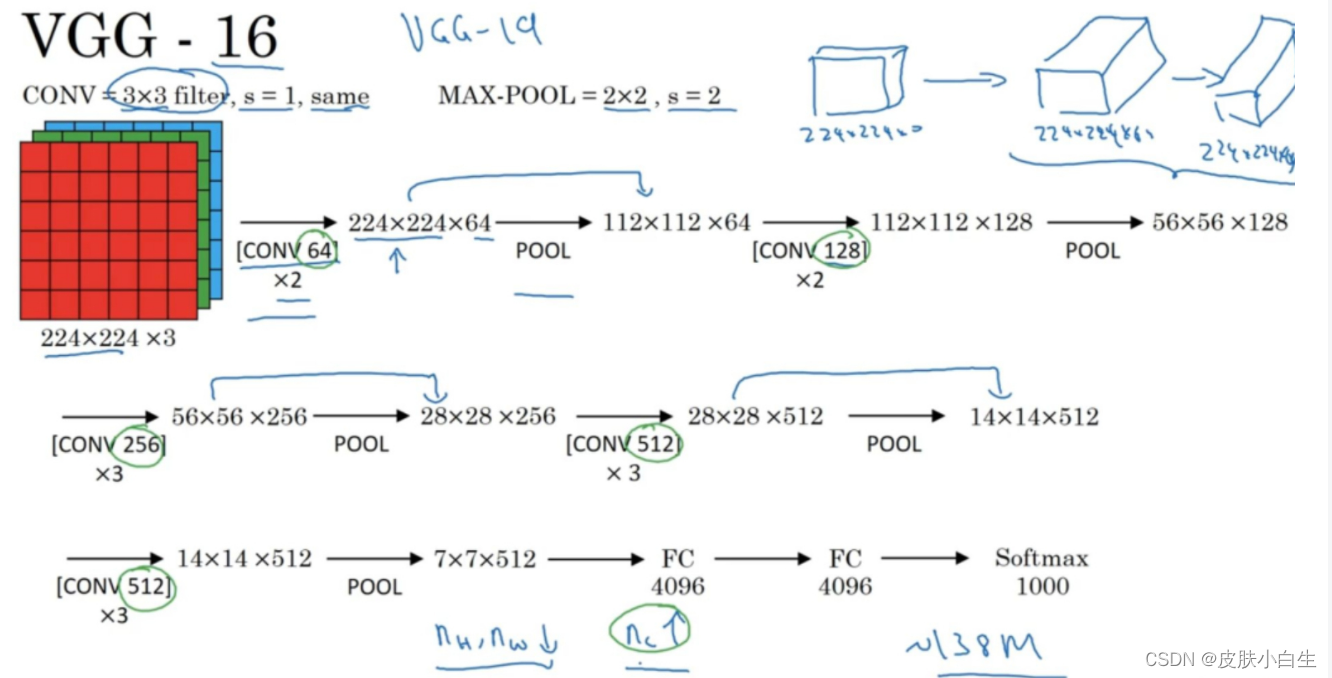
Coursera吴恩达《深度学习》课程总结(全)
这里有Coursera吴恩达《深度学习》课程的完整学习笔记,一共5门课:《神经网络和深度学习》、《改善深层神经网络》、《结构化机器学习项目》、《卷积神经网络》和《序列模型》, 第一门课:神经网络和深度学习基础,介绍一…...

C# 操作PDF表单 - 创建、填写、删除PDF表单域
通常情况下,PDF文件是不可编辑的,但PDF表单提供了一些可编辑区域,允许用户填写和提交信息。PDF表单通常用于收集信息、反馈或进行在线申请,是许多行业中数据收集和交换的重要工具。 PDF表单可以包含各种类型的输入控件࿰…...

Astropy:探索宇宙奥秘的Python工具箱
Astropy:探索宇宙奥秘的Python工具箱 什么是Astropy库? Astropy 是一个面向天文学领域的 Python 库,旨在提供常用的天文学数据结构、单位转换、物理常数以及天文学计算方法等功能。它为天文学家和研究人员提供了丰富的工具,用于处理和分析天文…...

java数据结构与算法刷题-----LeetCode684. 冗余连接
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 并查集 并查集 解题思路:时间复杂度O( n ∗ l o g 2…...
循环神经网络简介
卷积神经网络相当于人类的视觉,但是它并没有记忆能力,所以它只能处理一种特定的视觉任务,没办法根据以前的记忆来处理新的任务。比如,在一场电影中推断下一个时间点的场景,这个时候仅依赖于现在的场景还不够࿰…...
计算机网络 子网掩码与划分子网
一、实验要求与内容 1、需拓扑图和两个主机的IP配置截图。 2、设置网络A内的主机IP地址为“192.168.班内学号.2”,子网掩码为“255.255.255.128”,网关为“192.168.班内学号.1”;设置网络B内的主机IP地址为“192.168.班内学号100.2”&#…...

HUD抬头显示器中如何设计LCD的阳光倒灌实验
关键词:阳光倒灌实验、HUD光照温升测试、LCD光照温升测试、太阳光模拟器 HUD(Head-Up Display,即抬头显示器)是一种将信息直接投影到驾驶员视线中的技术,通常用于飞机、汽车等驾驶舱内。HUD系统中的LCD(Liq…...

Shoplazza闪耀Shoptalk 2024,新零售创新解决方案引领行业新篇章!
在近期举办的全球零售业瞩目盛事——Shoptalk 2024大会上,全球*的零售技术平台-店匠科技(Shoplazza)以其*的创新实力与前瞻的技术理念,成功吸引了与会者的广泛关注。此次盛会于3月17日至20日在拉斯维加斯曼德勒湾隆重举行,汇聚了逾万名行业精英。在这场零售业的盛大聚会上,Shop…...

Linux:sprintf、snprintf、vsprintf、asprintf、vasprintf比较
这些函数都在stdio.h里,不过不同系统不同库,有些函数不一定提供。 1. sprintf 函数原型: int sprintf (char *str, const char *format, ...); extern int sprintf (char *__restrict __s, const char *__restrict __format, ...); 功能是将…...

Github远程仓库改名字之后,本地git如何配置?
文章目录 缘由解决方案 缘由 今天在github创建一个仓库,备份一下本地电脑上的资料。起初随便起一个仓库名字,后来修改之。既然远程仓库改名,那么本地仓库需要更新地址。这里采用SSH格式。 解决方案 如果你的GitHub仓库改名了,你…...
4.10)
Objective-C学习笔记(ARC,分类,延展)4.10
1.自动释放池autoreleasepool:存入到自动释放池的对象,在自动释放池销毁时,会自动调用池内所有对象的release方法。调用autorelease方法将对象放入自动释放池。 Person *p1 [ [ [ Person alloc ] init ] autorelease]; 2.在类方法里写一个…...
02 Git 之IDEA 集成使用 GitHub(Git同时管理本地仓库和远程仓库)
2 .IDEA 集成使用 GitHub(Git同时管理本地仓库和远程仓库) 首先在 IDEA 的设置中绑定 GitHub 的账号 先创建一个 test1.txt 文件,内容为 aaa. 最上一栏 VCS, SHARE ON GitHub,然后选择要发送到远程仓库的文件即可。…...

CSS滚动条样式修改
前言 目前我们可以通过 CSS伪类 来实现滚动条的样式修改,以下为修改滚动条样式用到的CSS伪类: ::-webkit-scrollbar — 整个滚动条 ::-webkit-scrollbar-button — 滚动条上的按钮 (上下箭头) ::-webkit-scrollbar-thumb — 滚动条上的滚动滑块 ::-web…...

《零秒思考》像麦肯锡精英一样思考 - 三余书屋 3ysw.net
零秒思考:像麦肯锡精英一样思考 大家好,今天我们要深入探讨的著作是《零秒思考》。在领导提出问题时,我们常常会陷入沉思,却依然难以有所进展,仿佛原地踏步,但是身边的同事却能够立即给出清晰的回答。这种…...

使用docker制作Android镜像(实操可用)
一、安装包准备 1、准备jdk 下载地址:Java Downloads | Oracle 注意版本!!!!!! 我下载的jdk17,不然后面构建镜像报错,就是版本不对 2、准备安装的工具包 ttps://dev…...

大厂MVP技术JAVA架构师培养
课程介绍 这是一个很强悍的架构师涨薪计划课程,课程由专家级MVP讲师进行教学,分为是一个章节进行分解式面试及讲解,不仅仅是面试,更像是一个专业的架构师研讨会课程。课程内容从数据结构与算法、Spring Framwork、JVM原理、 JUC并…...

uniapp实现文件和图片选择上传功能实现
主要介绍了uni-file-picker文件选择上传,本文通过实例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友可以参考下 上传一张: <template><view class="container example"><uni-forms ref="baseForm" …...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
