python统计分析——一般线性回归模型
参考资料:python统计分析【托马斯】
当我想用一个或多个其他的变量预测一个变量的时候,我们可以用线性回归的方法。
例如,当我们寻找给定数据集的最佳拟合线的时候,我们是在寻找让下式的残差平方和最小的参数(k,d):
其中,k是线的斜率,d是截距。残差是观测值和预测值之间的差异。
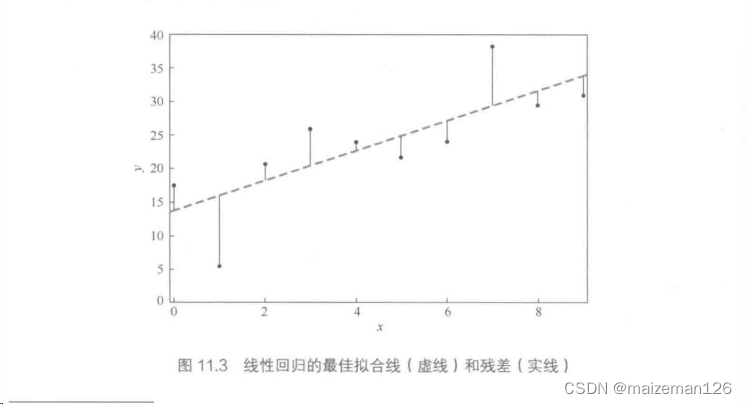
由于线性回归方程是用最小化残差平方和的方法来解决的,线性回归又是也成为普通最小二乘法(OLS)回归。
这里注意:与相关性相反,x和y之间的这种关系不再是对称的;它假设x值是精确的,所有的变异性都在于残差。
1、决定系数
我们约定:是数据集中的观测值,
为模型计算得到的于
相对应的预测值,
为所有
的平均值。那么:
是模型平方和,或回归平方和,或可解释平方和。
是残差平方和,或误差平方和。
是总平方和,它等于样本方差乘以n-1。
决定系数一般表示为:
由于
所以:
用文字表达:决定系数就是模型的可解释平方和与总平方和的比值。
对于简单线性回归(即直线拟合),决定系数就是相关系数r的平方。如果我们的自变量和因变量之间存在非线性关系,那么简单的相关性和决定系数会对结果造成误导。
2、带置信区间的直线
对于单变量分布,基于标准差的置信区间表示我们期望包含95%的数据的区间(用于数据);而基于平均数标准误的置信区间表示95%概率下包含真正均值的区间(用于参数)。如下:

3、曲线拟合
为了了解如何使用不同的模型来评估给定的数据集,让我们来看一个简单的例子:拟合一个有噪声的、略微二次项弯曲的曲线。让我们从numpy中实现的算法开始,然后用线性、二次方、三次方曲线来拟合数据。
代码如下:
# 导入库
import numpy as np
import matplotlib.pyplot as plt# 生成一个有噪声、略微二次项弯曲的数据集
x=np.arange(100)
y=150+3*x+0.3+x**2+5*np.random.randn(len(x))# 线性拟合、二次方拟合、三次方拟合
# 创建设计矩阵
M1=np.vstack((np.ones_like(x),x)).T
M2=np.vstack((np.ones_like(x),x,x**2)).T
M3=np.vstack((np.ones_like(x),x,x**2,x**3)).T# 解方程
p1=np.linalg.lstsq(M1,y)
p2=np.linalg.lstsq(M2,y)
p3=np.linalg.lstsq(M3,y)np.set_printoptions(precision=3)
print('the coefficients from the linear fit:{0}'.format(p1[0]))
print('the coefficients from the quadratic fit:{0}'.format(p2[0]))
print('the coefficients from the cubic fit:{0}'.format(p3[0]))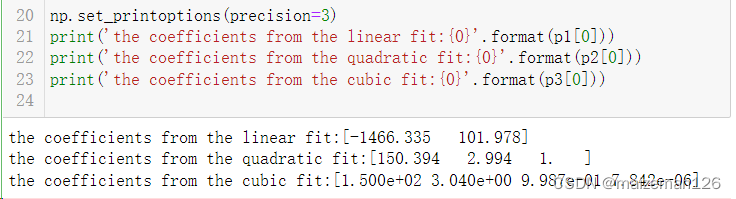
# 计算x对应的预测值
p1_y=-1466.335+101.978*x
p2_y=150.394+2.994*x+x**2
p3_y=150+3.04*x+0.9987*x**2+7.842*(10**(-6))*x**3# 作图
plt.rcParams['font.sans-serif']="SimHei" # 设置中文显示
plt.rcParams['axes.unicode_minus']=False # 设置负号显示
plt.scatter(x,y,c="black",s=0.1,label="数据")
plt.plot(x,p1_y,"b:",label="线性拟合")
plt.plot(x,p2_y,"r--",label="二次方拟合")
plt.plot(x,p3_y,'g-.',label="三次方拟合")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()显示图片如下

如果我们想找到哪个才是拟合的“最好的”,我们可以使用statsmodels提供的工作来再次拟合模型。使用statsmodels,我们不仅可以得到最佳拟合参数,还能得到关于模型的许多价值的额外信息。python代码如下:
import statsmodels.api as sm
import statsmodels.formula.api as smfRes1=sm.OLS(y,M1).fit()
Res2=sm.OLS(y,M2).fit()
Res3=sm.OLS(y,M3).fit()# 以Res1为例输出结果
print(Res1.summary2())
print('the AIC-value is {0:4.1f} for the linear fit ,\n{1:4.1f} for the quadratic fit ,and \n {2:4.1f} for the cubic fit'.format(Res1.aic,Res2.aic,Res3.aic))
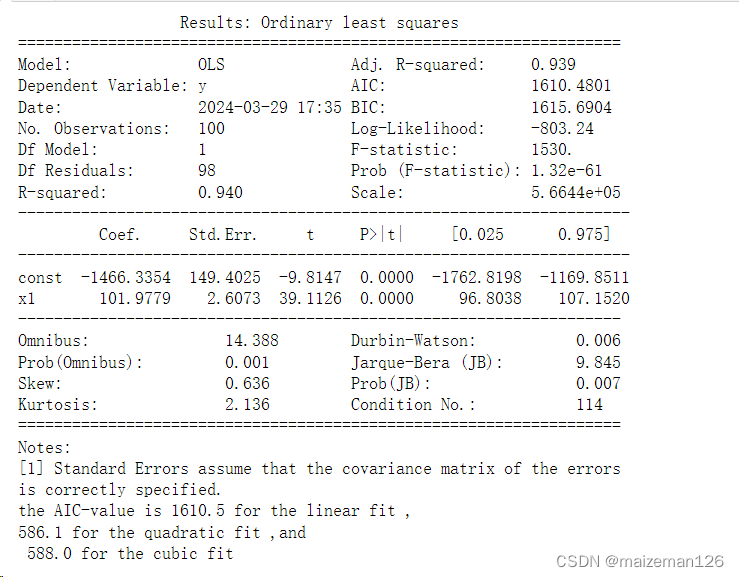
在这里,我们需要知道AIC值(Akaike信息准则)可用于评估模型的质量:AIC值越低,模型越好。我们看到,二次模型的AIC值最小,因此是最好的模型:它提供了与三次方模型相同的拟合质量,但使用较少的参数来得到该质量。
下面我们再用公式语言执行相同的拟合,但不需要手动生成设计矩阵,以及如何提取模型参数、标准误和置信区间。值得注意的是,使用pandas数据框允许Python添加单独参数的信息。
import pandas as pd
import statsmodels.formula.api as smf# 将数据转化为pandas的dataframe格式
df=pd.DataFrame({"x":x,"y":y})# 拟合模型,并展示结果
Res1F=smf.ols("y~x",df).fit()
Res2F=smf.ols("y~x+I(x**2)",df).fit()
Res3F=smf.ols("y~x+I(x**2)+I(x**3)",df).fit()# 作为示例,显示二次方拟合的参数
print(Res2F.params)
print(Res2F.bse)
print(Res2F.conf_int())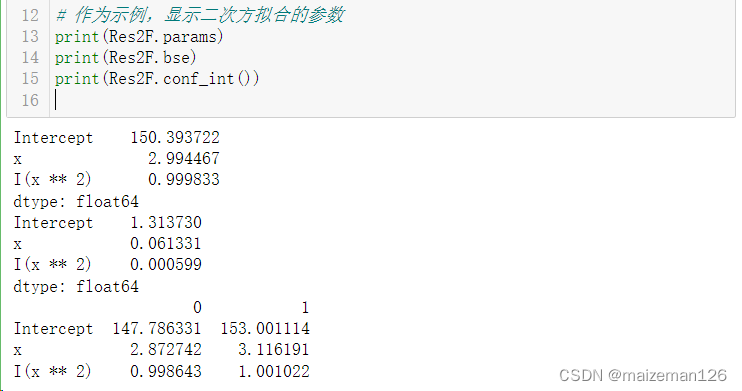
相关文章:

python统计分析——一般线性回归模型
参考资料:python统计分析【托马斯】 当我想用一个或多个其他的变量预测一个变量的时候,我们可以用线性回归的方法。 例如,当我们寻找给定数据集的最佳拟合线的时候,我们是在寻找让下式的残差平方和最小的参数(k,d): 其…...

【cocos creator】【TS】贝塞尔曲线,地图之间显示曲线
参考: https://blog.csdn.net/Ctrls_/article/details/108731313 https://blog.csdn.net/qq_28299311/article/details/104009804 const { ccclass, property } cc._decorator;ccclass export default class creatPoint extends cc.Component {property(cc.Node)bu…...

COMFYUI换脸ReActor报错Value not in list: face_restore_model: ‘codeformer.pth‘解决
Value not in list: face_restore_model: codeformer.pth not in [none, GFPGANv1.3.pth] 搜了下没找到答案,最后看github官方的指引: You can download models here: https://huggingface.co/datasets/Gourieff/ReActor/tree/main/models/facerestore…...

深入理解Java中的字段与属性的区别
1、Java中的属性和字段有什么区别? 答:Java中的属性(property),通常可以理解为get和set方法。 而字段(field),通常叫做“类成员”,或 "类成员变量”,有时也叫“域”,理解为“数据成员”&…...

【Locust分布式压力测试】
Locust分布式压力测试 https://docs.locust.io/en/stable/running-distributed.html Distributed load generation A single process running Locust can simulate a reasonably high throughput. For a simple test plan and small payloads it can make more than a thousan…...

富格林:出金异常警惕黑幕陷阱受骗
富格林悉知,在做单出金时落入黑幕陷阱亏损后,需尽快发现和总结错误,用心筹维权谋安全出金盈利方法并追回亏损。因为黄金市场优势众多,众多的投资者进入市场投资,但因为经验不足,在面对黑幕陷阱是获取无法及…...

Docker - Nginx
博文目录 文章目录 说明命令 说明 Docker Hub Nginx 数据卷数据卷印射在容器内的路径nginx.conf/etc/nginxnginx.html/usr/share/nginx/htmlnginx.log/var/log/nginx 容器内的路径说明/etc/nginx/nginx.conf配置文件/etc/nginx/conf.d配置目录/usr/share/nginx/html静态目录/…...

免费搭建幻兽帕鲁服务器(Palworld免费开服教程)
随着互联网技术的不断发展和普及,网络游戏已经成为了人们休闲娱乐的重要方式之一。而在众多网络游戏中,幻兽帕鲁以其独特的游戏设定和玩法,吸引了大量玩家的关注。为了满足广大玩家的需求,本文将介绍如何免费搭建幻兽帕鲁服务器&a…...
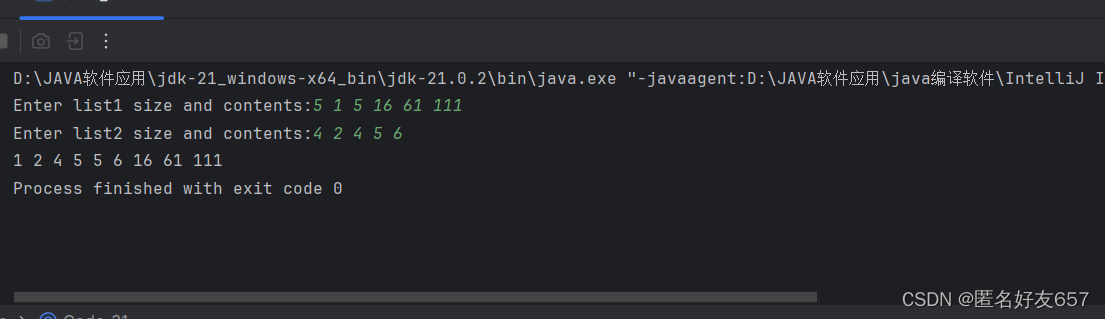
作业习题
实验代码: import java.util.Scanner;class chazhao {public static void main(String[] args) {Scanner scnew Scanner(System.in);System.out.println("请输入你要的数组");String line sc.nextLine();String[] lineArrline.split(" ");int[…...
解决unbuntu更新到23.10 mantic firefox无法使用的问题
产看历史版本号: 升级到最新版本后查看: roottesthost01:/home/test/Desktop# lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 23.10 Release: 23.10 Codename: mantic 打开firefox发现图标找…...

idea常用配置——注释快捷键
1、单行注释:使用 Ctrl / 可以添加或删除当前行的注释。如果你想要给某一行添加注释,只需要将光标放在那一行,然后按下 Ctrl / 即可。如果你想要删除那一行的注释,同样只需要将光标放在那一行,然后再次按下 Ctrl /。…...

Hidl 学习总结 2
1、Android apk 调用Hidl处理 app添加对应的hidl jar包 2、MainActivity 添加如下代码 package com.example.test2;import androidx.appcompat.app.AppCompatActivity; import vendor.hardware.test.V1_0.ITest; import vendor.hardware.test.V1_0.ITestCmdCallback; import …...
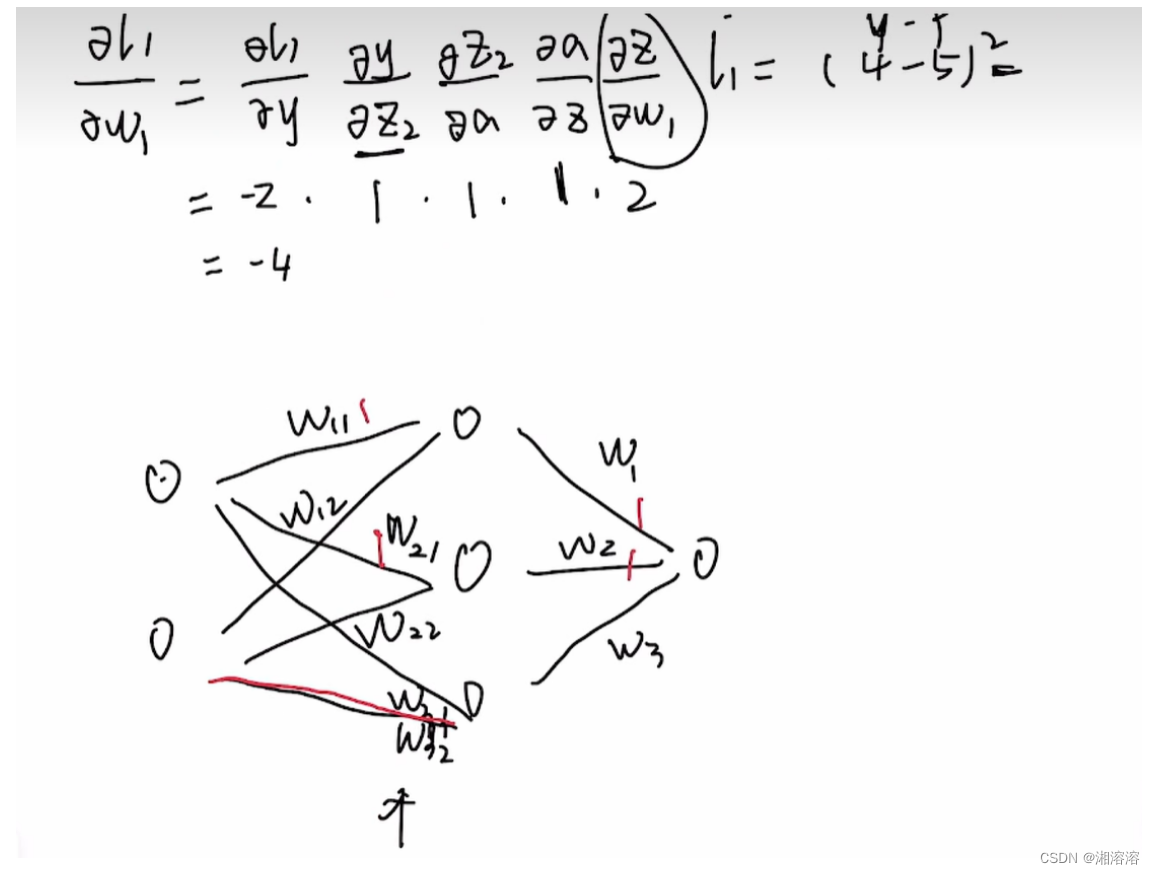
深度学习学习日记4.7
1.梯度下降 w 新 w旧 - 学习率梯度 训练的目的就是让 loss 减小 2.前向传播进行预测, 反向传播进行训练(每一个参数通过梯度下降进行更新参数),(1前向传播 2求 loss 3反向传播 4梯度更新) 能够让损失下降的参数,就是更好的参数。 损失…...

五一假期来临,各地景区云旅游、慢直播方案设计与平台搭建
一、行业背景 经文化和旅游部数据中心测算,今年清明节假期3天全国国内旅游出游1.19亿人次,按可比口径较2019年同期增长11.5%;国内游客出游花费539.5亿元,较2019年同期增长12.7%。踏青赏花和户外徒步成为假期的热门出游主题。随着…...

自动驾驶中的交通标志识别原理及应用
自动驾驶中的交通标志识别原理及应用 附赠自动驾驶学习资料和量产经验:链接 概述 道路交通标志和标线时引导道路使用者有秩序使用道路,以促进道路行车安全,而在驾驶辅助系统中对交通标志的识别则可以不间断的为整车控制提供相应的帮助。比如…...

数据挖掘入门项目二手交易车价格预测之建模调参
文章目录 目标步骤1. 调整数据类型,减少数据在内存中占用的空间2. 使用线性回归来简单建模3. 五折交叉验证4. 模拟真实业务情况5. 绘制学习率曲线与验证曲线6. 嵌入式特征选择6. 非线性模型7. 模型调参(1) 贪心调参(2)…...
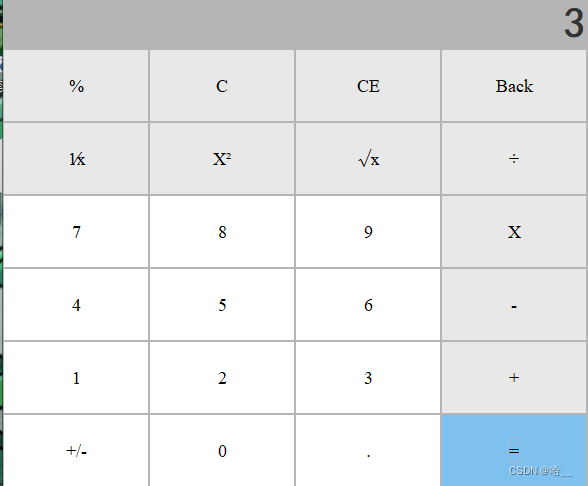
【Java】Java使用Swing实现一个模拟计算器(有源码)
📝个人主页:哈__ 期待您的关注 今天翻了翻之前写的代码,发现自己之前还写了一个计算器,今天把我之前写的代码分享出来。 我记得那会儿刚学不会写,写的乱七八糟,但拿来当期末作业还是不错的哈哈。 直接上…...

MC9S12DJ64微控制器
这份文件是关于Freescale的MC9S12DJ64微控制器的用户指南,包含了关于该设备的详细信息和使用说明。以下是核心内容的整理: 产品信息: 产品信息详细描述如下: 1. **产品名称**:- MC9S12DJ64微控制器单元(MCU)2. **核心…...

小程序打开空白的问题处理
小程序打开是空白的,如下: 这个问题都是请求域名的问题: 一、检查服务器域名配置了 https没有,如果没有,解决办法是申请个ssl证书,具体看这里 https://doc.crmeb.com/mer/mer2/4257 二、完成第一步后&#…...
langchain + azure chatgpt组合配置并运行
首先默认你已经有了azure的账号。 最重要的是选择gpt-35-turbo-instruct模型、api_version:2023-05-15,就这两个参数谷歌我尝试了很久才成功。 我们打开https://portal.azure.com/#home,点击更多服务: 我们点击Azure OpenAI&#…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
