8.排序(直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序)的模拟实现
1.排序的概念及其运用
1.1排序的概念
-
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
-
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
-
内部排序:数据元素全部放在内存中的排序。
-
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法
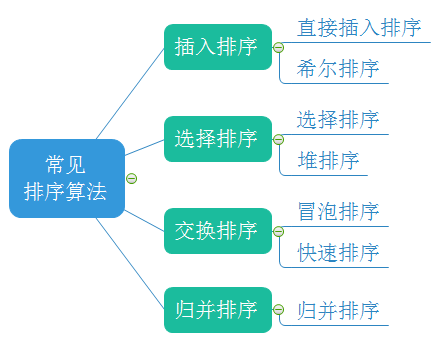
2.常见排序算法的实现
2.1插入排序
1.直接插入排序
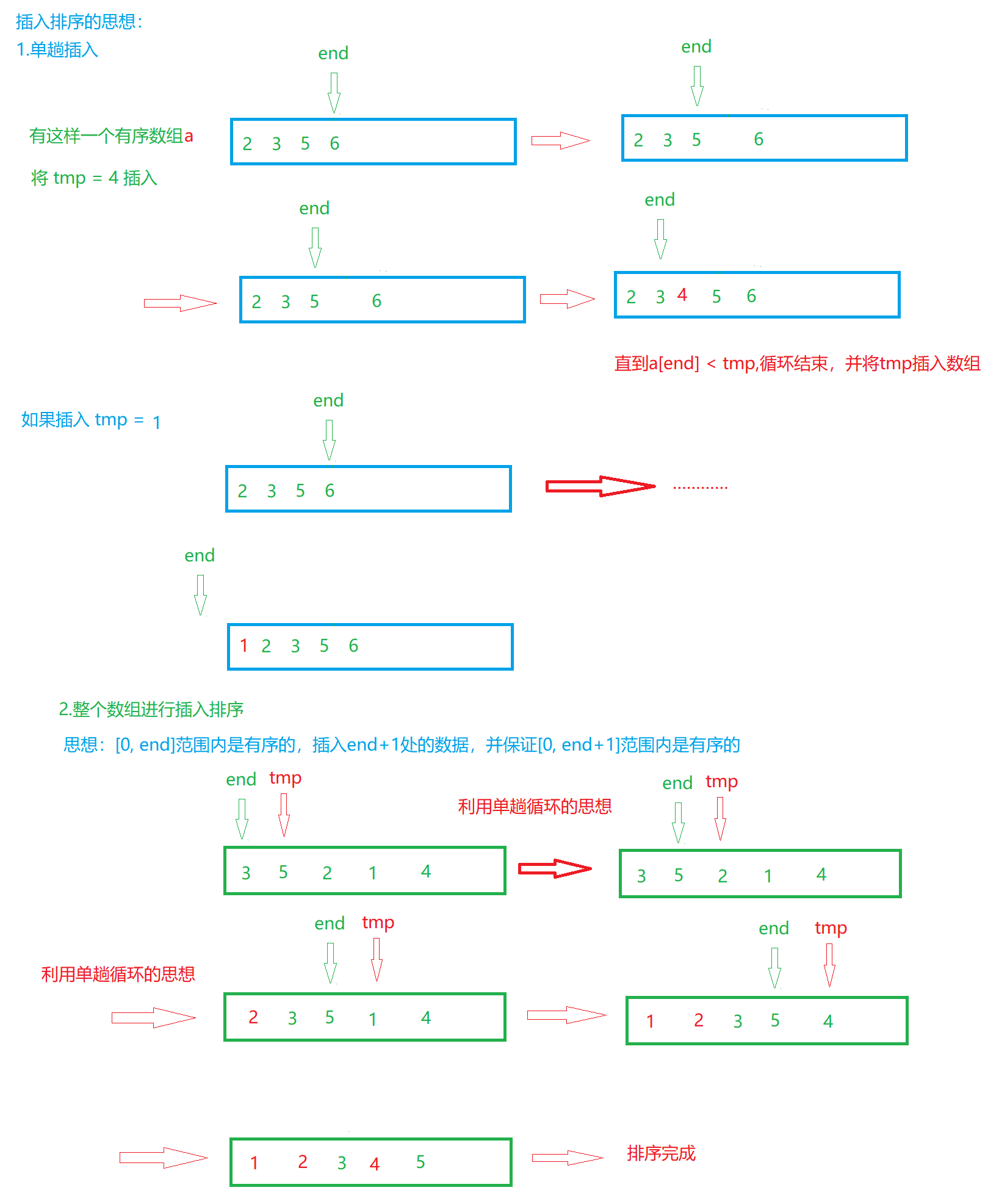
// 最坏时间复杂度O(N^2) -- 原数组是逆序
// 最好时间复杂度O(N) -- 原数组是顺序有序// 直接插入排序
void InsertSort(int* a, int n)
{// 在[0,end]范围内 插入第 end+1 个数据 并使[0, end+1]范围内的数据有序for (int i = 0; i < n - 1; ++i){// 根据上面的图解来理解a[end] 和 tmp的下标int end = i;int tmp = a[end + 1];// 当end >= 0,那么就继续比较a[end]与tmpwhile (end >= 0){// 将数组排列为一个升序数组if (a[end] > tmp){// 如果前一个数据a[end],大于后一个数据tmp// 直接用end位置的数据覆盖end + 1的数据,保持tmp不发生改变a[end + 1] = a[end];// 迭代--end;}else{break;}}// 当循环结束,end + 1处的数据是旧数据,需要使用tmp更新a[end + 1] = tmp;}
}
打印数组(便于我们来观察排序)
void PrintArray(int* a, int n)
{for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}
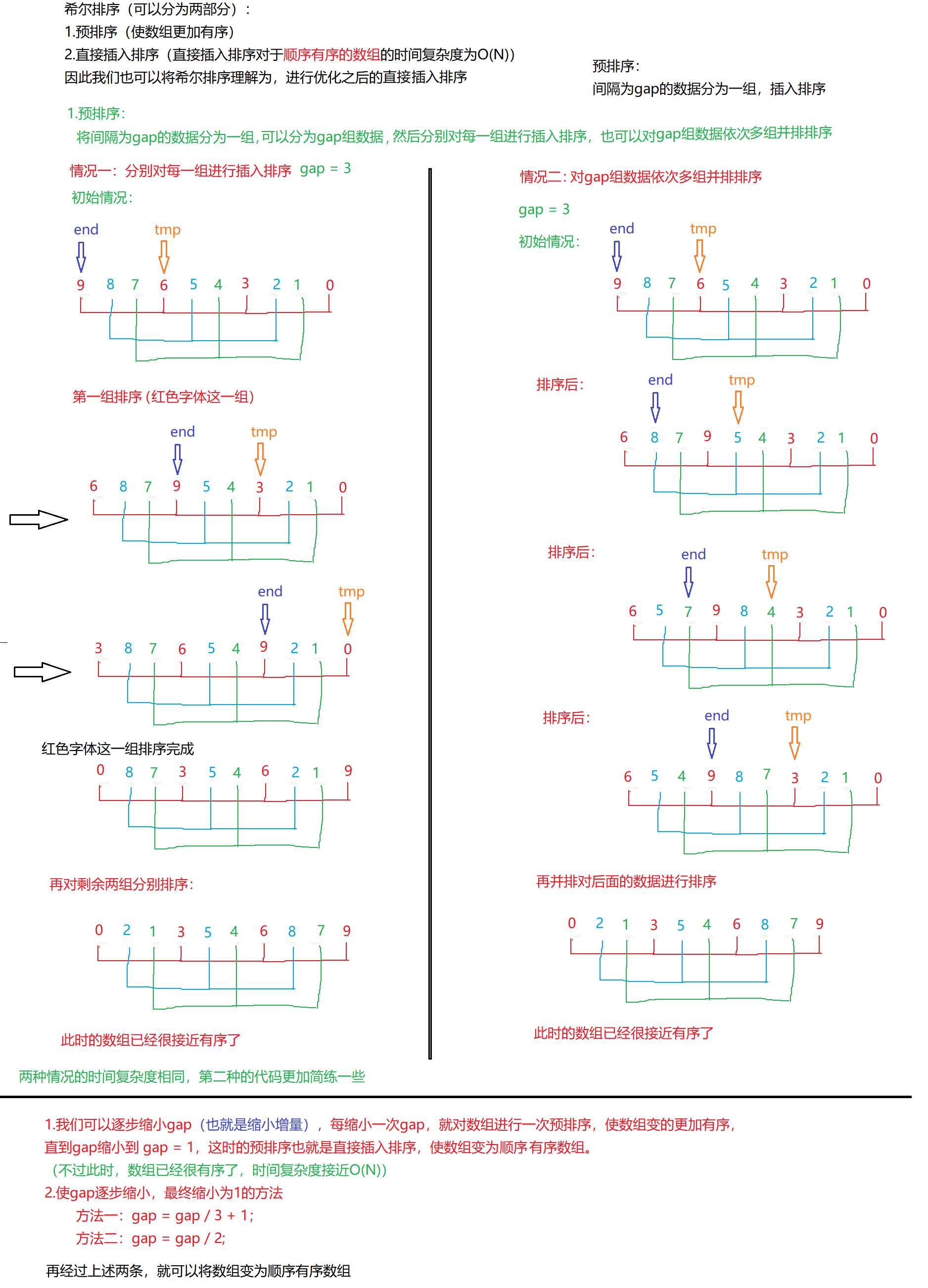
2.希尔排序( 缩小增量排序 )
// 情况二:
// 注:希尔排序的时间复杂度,太过复杂,我们可以默认理解希尔排序的时间复杂度为O(N^1.3),
// 当数据量很大时,是比堆排序O(N*logN)略差的
// 希尔排序的时间复杂度为O(N^1.3)// 这个函数采用的是多组并排排序的方法来实现希尔排序
void ShellSort(int* a, int n)
{// 将间隔为gap的数据分为一组int gap = n;// gap > 1 预排序// gap == 1 直接插入排序// 当while循环结束,说明缩小gap间隙最终为1,数组已经很接近有序了while (gap > 1){// 下面是缩小间隙的两种方法,本文采用第二种// gap = gap / 2;gap = gap / 3 + 1; // 当for循环结束,gap为n的所有组数据就排列好了// 下面for循环的算法就是,直接插入排序的算法,// 只是改变了a[end]和tmp下标之间的距离for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];// 直到end < 0才可以停止比较while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
// 情况一: 分组进行排序
// 时间复杂度为:O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;// 间隔为gap的数据// 当j改变,就是代表一组数据排列完成,将要对下一组数据进行排序for (int j = 0; j < gap; ++j){// 间隔为gap一组排序for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
2.2 选择排序
1.直接选择排序
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
直接选择排序:
-
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
-
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
-
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
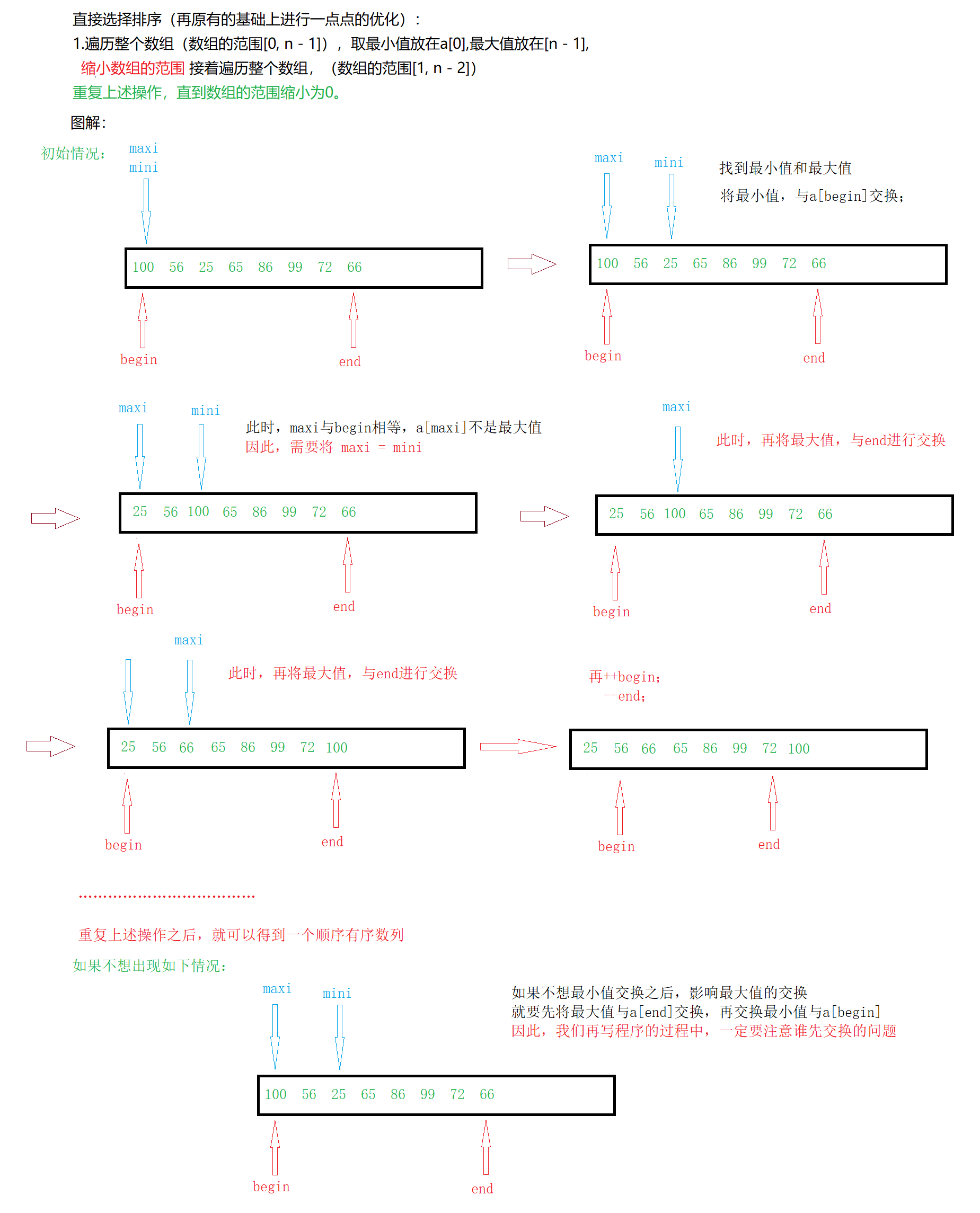
// 直接选择排序最坏时间复杂度:O(N^2)
// 直接选择排序最好时间复杂度:O(N^2)
void SelectSort(int* a, int n)
{// 初始化begin和end下标int begin = 0, end = n - 1;// 只有begin小于end时,才可以继续while (begin < end){// 选出最小的放begin位置// 选出最大的放end位置// 将标识最大值和最小值的下标都初始化为beginint mini = begin, maxi = begin;// 当for循环结束时,a[mini]为最小值,a[maxi]为最大值,在[begin,end]范围内for (int i = begin + 1; i <= end; ++i){// 如果为真,那么i下标所在的元素就是最大值,所以更改最大值的下标maxi为iif (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}// 1.现将最小值a[mini]与初始位置的值进行交换Swap(&a[begin], &a[mini]);// 修正一下maxi// 如果初始位置的值是最大值,由于上面进行了交换,所以此时最大值的下标为mini// 因此,将mini赋值给maxiif (maxi == begin)maxi = mini;// 2.将最大值a[maxi]与末尾位置的值进行交换Swap(&a[end], &a[maxi]);// 迭代++begin;--end;}
}
2.堆排序
void AdjustDown(int* a, int n, int parent)
{int minChild = parent * 2 + 1;while (minChild < n){// 找出小的那个孩子if (minChild + 1 < n && a[minChild + 1] > a[minChild]){minChild++;}if (a[minChild] > a[parent]){Swap(&a[minChild], &a[parent]);parent = minChild;minChild = parent * 2 + 1;}else{break;}}
}// O(N*logN)
void HeapSort(int* a, int n)
{// 大思路:选择排序,依次选数,从后往前排// 升序 -- 大堆// 降序 -- 小堆// 建堆 -- 向下调整建堆 - O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// 选数 N*logNint i = 1;while (i < n){Swap(&a[0], &a[n - i]);AdjustDown(a, n - i, 0);++i;}
}
- 关于堆排序请查看作者的另一篇文章,堆排序。
2.3 交换排序
1.冒泡排序
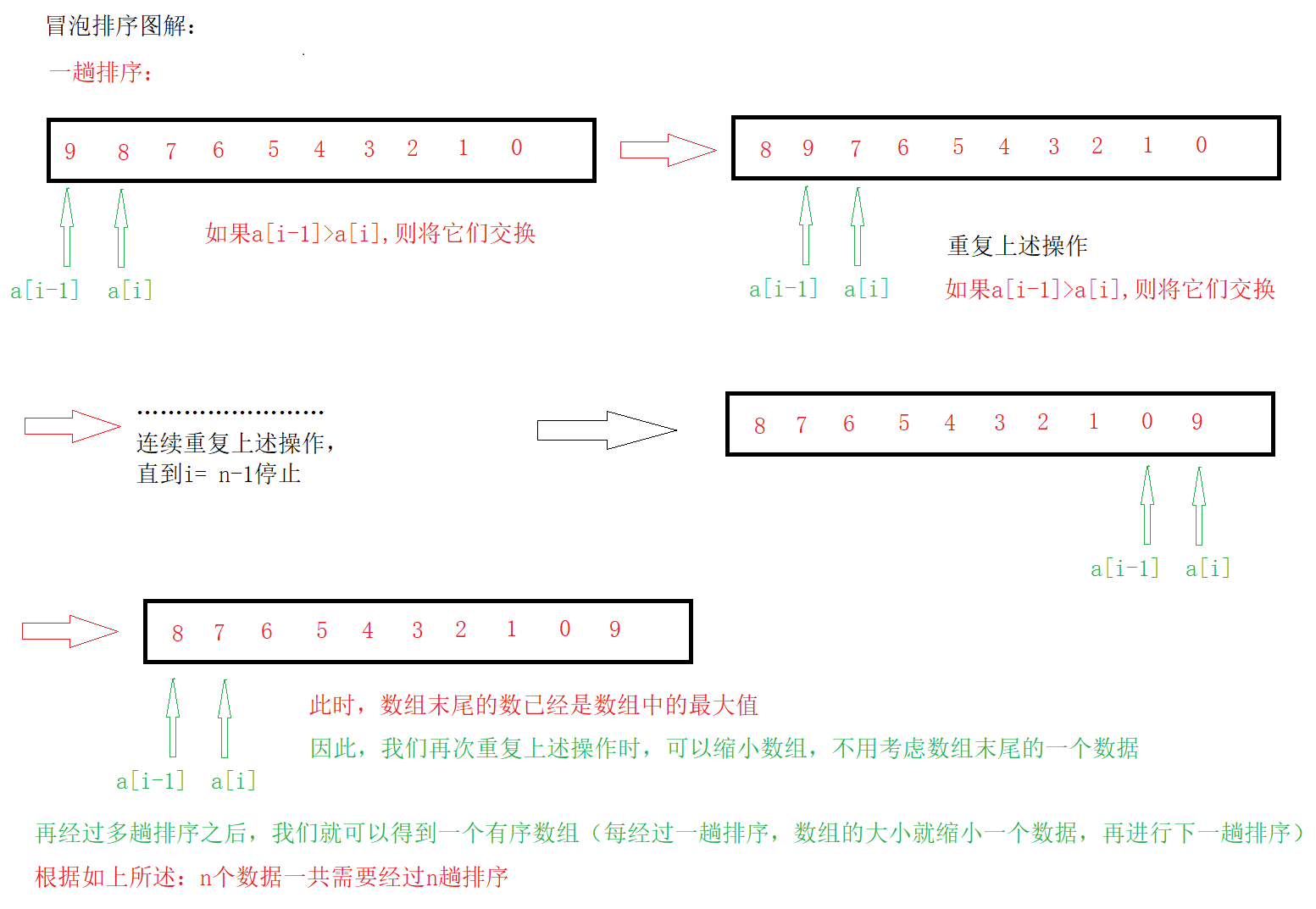
// 交换排序(冒泡排序)
// 冒泡排序最坏情况的时间复杂度:O(N^2)
// 冒泡最好情况的时间复杂度:O(N)
void BubbleSort(int* a, int n)
{// n是数组中元素的个数// 这个for代表趟数for (int j = 0; j < n; ++j){// 每一趟都会将exchange初始化为0// 如果还有a[i - 1] > a[i]存在,那么exchange就会被修改为1// 但是最后一趟时,数组已经是一个有序的数组了,因此exchange不会被修改int exchange = 0;// for代表了一趟中,a[i]与a[i - 1]迭代比较for (int i = 1; i < n - j; ++i){// a[i - 1]是下标较小的元素,a[i]是下标较大的元素// 当这个条件为真,那么交换两个元素的位置if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}
2.快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1.hoare版本
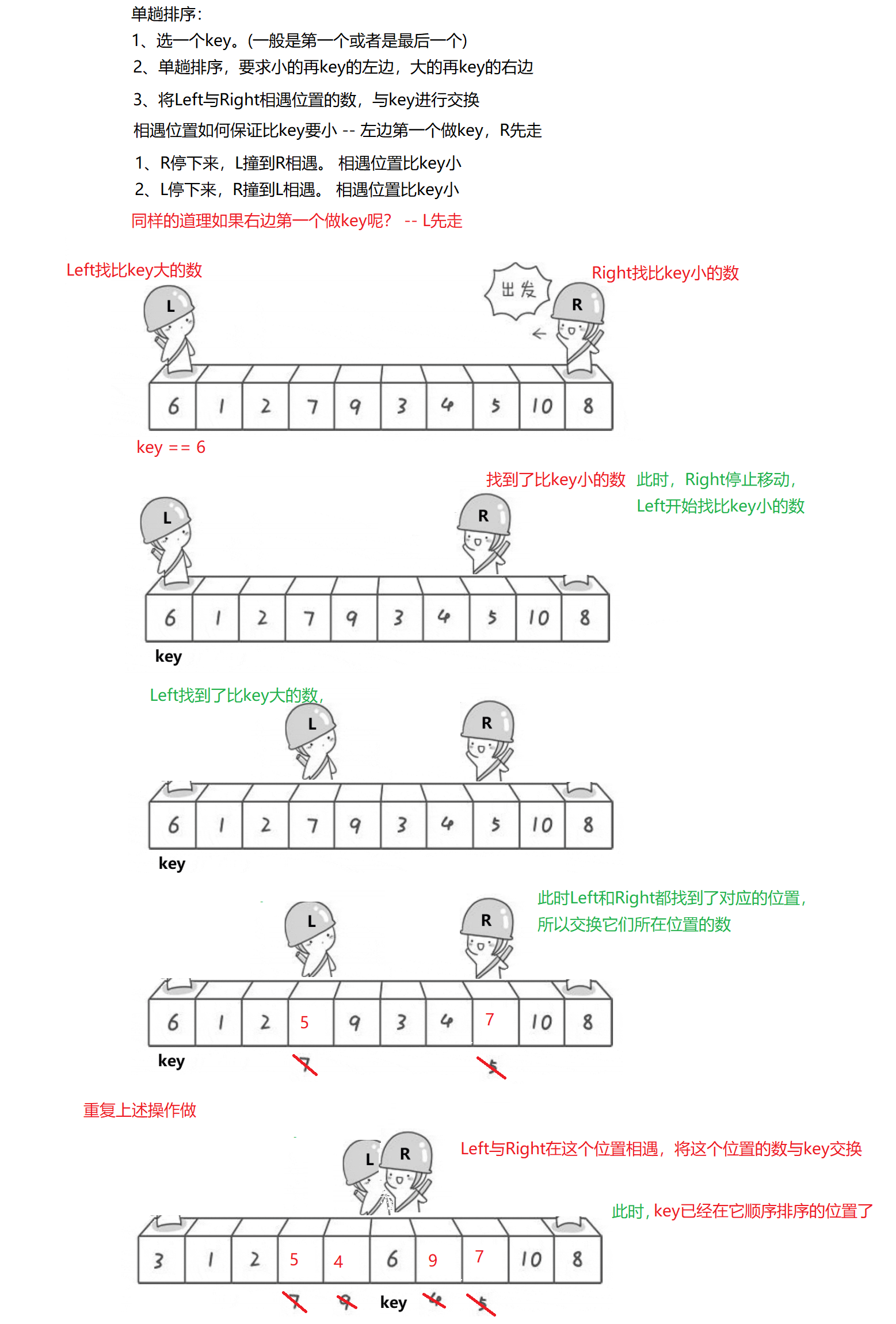
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// PartSort函数,是一趟(想要利用上述的方法将这个数组的元素排序,还需要很多趟,具体看后续的解释)
// 返回left和right相遇节点的下标
int PartSort(int* a, int left, int right)
{// 将左侧的下标定义为keyi下标int keyi = left;// 当left等于right说明两个人相遇了,那么就停止循环while (left < right){// Right需要找比a[keyi]小的数// 因此,如果a[right] >= a[keyi]为真,那么就继续循环// 注意:在循环的过程中一定要保证left < right,否则就没有意义了while (left < right && a[right] >= a[keyi]){--right;}// Lift需要找比a[keyi]大的数while (left < right && a[left] <= a[keyi]){++left;}// 如果此时left < right为真,那么就交换a[left]和a[right]if (left < right)Swap(&a[left], &a[right]);}// 此时,left和right都是相遇节点的下标,// 使用left赋值给meetiint meeti = left;// 将相遇节点的数据与keyi下标的数据进行交换Swap(&a[meeti], &a[keyi]);return meeti;
}
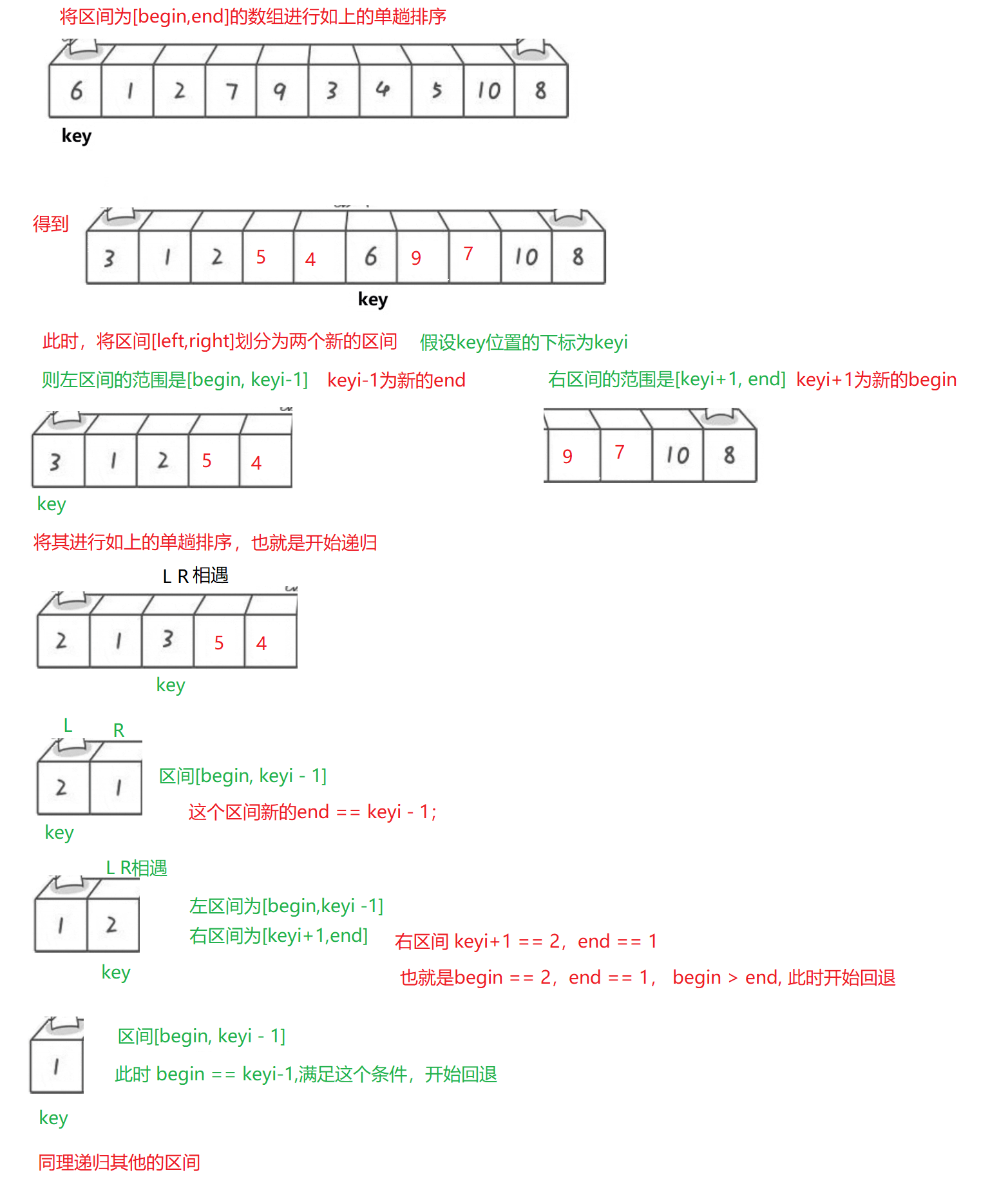
// 快速排序
void QuickSort(int* a, int begin, int end)
{// 必须满足begin小于end// 否则,就返回if (begin >= end){return;}// 先使用PartSort()函数对[begin,end]区间的数进行一趟排序// PartSort()的返回值是meeti,也就是相遇节点的下标,将其存放到keyiint keyi = PartSort(a, begin, end);// 以keyi为分割点,将[begin,end]区间分割为下面两个区间// [begin, keyi-1] keyi [keyi+1, end]// 左区间递归,和右区间递归QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
快速排序的优化

// 优化之后的代码// 三数取中
int GetMidIndex(int* a, int left, int right)
{// 数组中间的数的下标就是midint mid = left + (right - left) / 2;if (a[left] < a[mid]){// 此时a[mid]已经大于a[left],那么只要满足a[mid] < a[right],就返回a[mid]的下标// 满足a[left] > a[right],也就是a[mid]>a[left] > a[right],就返回a[left]的下标// 都不满足,也就是a[right]<a[left]<a[mid],就返回a[right]的下标if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// [left, right] -- O(N)
// hoare
// PartSort1函数,是一趟(单趟排序)
int PartSort1(int* a, int left, int right)
{// 三数取中,得到left,right,left + (right - left) / 2中,中间大的哪个数int mid = GetMidIndex(a, left, right);// 此处的mid就是指中间大的哪个数的下标//printf("[%d,%d]-%d\n", left, right, mid);// 将中间大的数,放在数组的最左侧Swap(&a[left], &a[mid]);// keyi依旧是最左侧的数的下标(继承优化前的代码,不需要做出改动)int keyi = left;while (left < right){// R找小while (left < right && a[right] >= a[keyi]){--right;}// L找大while (left < right && a[left] <= a[keyi]){++left;}if (left < right)Swap(&a[left], &a[right]);}int meeti = left;Swap(&a[meeti], &a[keyi]);return meeti;
}// 快速排序函数
void QuickSort(int* a, int begin, int end) // 分区间递归
{// 必须保证begin >= end为假,才可以继续迭代if (begin >= end){return;}// 8的取值,参考经验,8比较合适// 当[begin,end]区间的元素小于等于8时,这个时候再分小区间,后三层小区间有很多个// 为了减小栈的开销,当end - begin <= 8为真时,采用直接插入排序来将数组进行排序(此时的数组已经很接近有序了,因此使用直接插入排序,并不会降低太多的效率)if (end - begin <= 8) {// 小区间优化,最后三层用直接插入排序InsertSort(a + begin, end - begin + 1);}else{// 先使用PartSort()函数对[begin,end]区间的数进行一趟排序// PartSort()的返回值是meeti,也就是相遇节点的下标,将其存放到keyiint keyi = PartSort1(a, begin, end);// 以keyi为分割点,将[begin,end]区间分割为下面两个区间// [begin, keyi-1] keyi [keyi+1, end]// 迭代左区间// 迭代右区间QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}
2.挖坑法(重要)
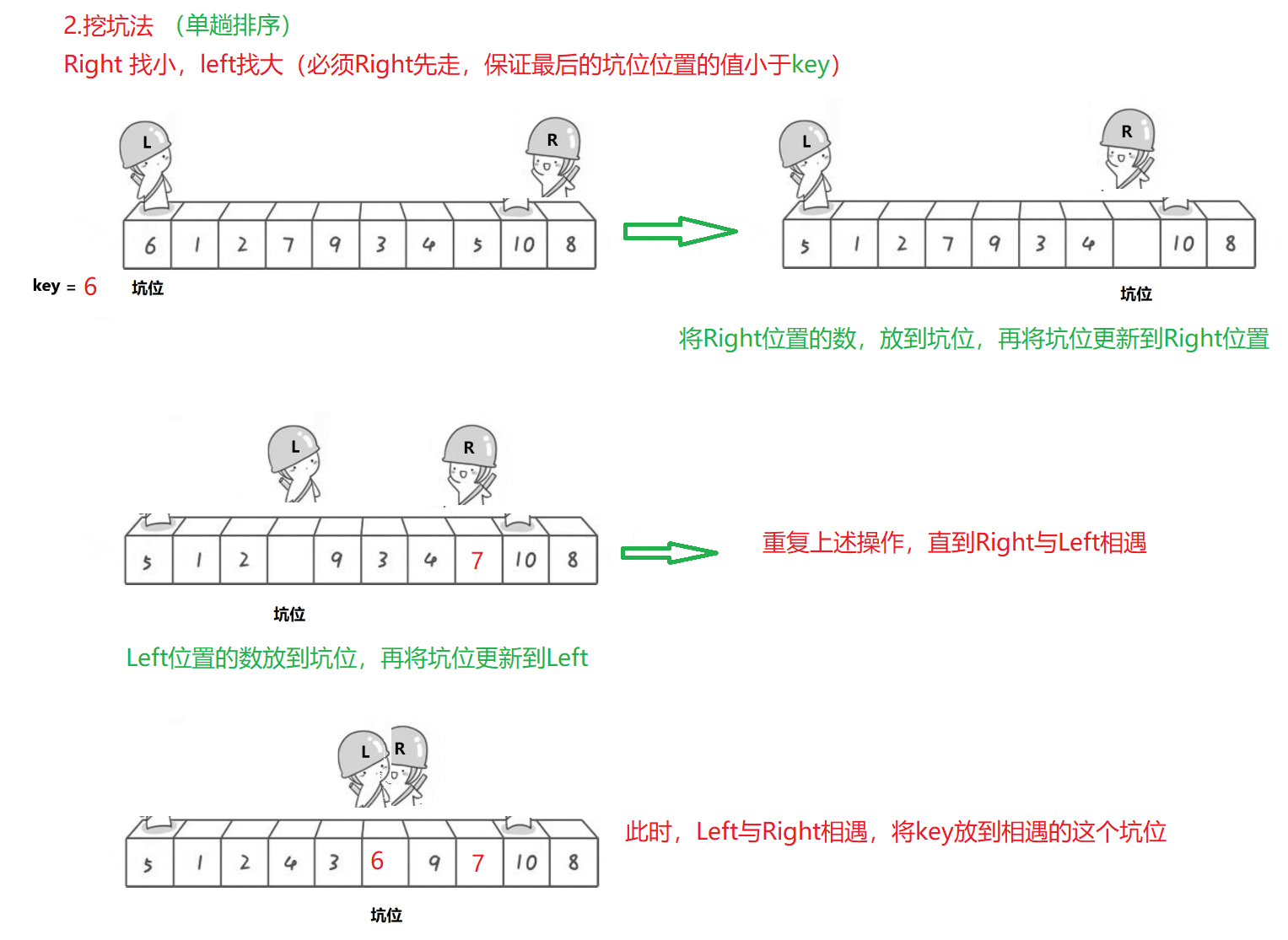
// 三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 挖坑法
int PartSort2(int* a, int left, int right)
{// 三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);// 将key值初始化为a[left]// 将坑位的下标hole初始化为leftint key = a[left];int hole = left;while (left < right){// 右边找小,填到左边坑while (left < right && a[right] >= key){--right;}a[hole] = a[right];// 此时right对应的下标成为新的坑位hole = right;// 左边找大,填到右边坑while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}// 当left和right相遇,将key值放入这个坑位(最后的这个坑位)a[hole] = key;return hole;
}// [begin, end]
void QuickSort(int* a, int begin, int end) // 分区间递归
{if (begin >= end){return;}if (end - begin <= 8) // 8的取值,参考经验,8比较合适{InsertSort(a + begin, end - begin + 1);// 小区间优化,最后三层用插入排序}else{int keyi = PartSort2(a, begin, end);//[begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}
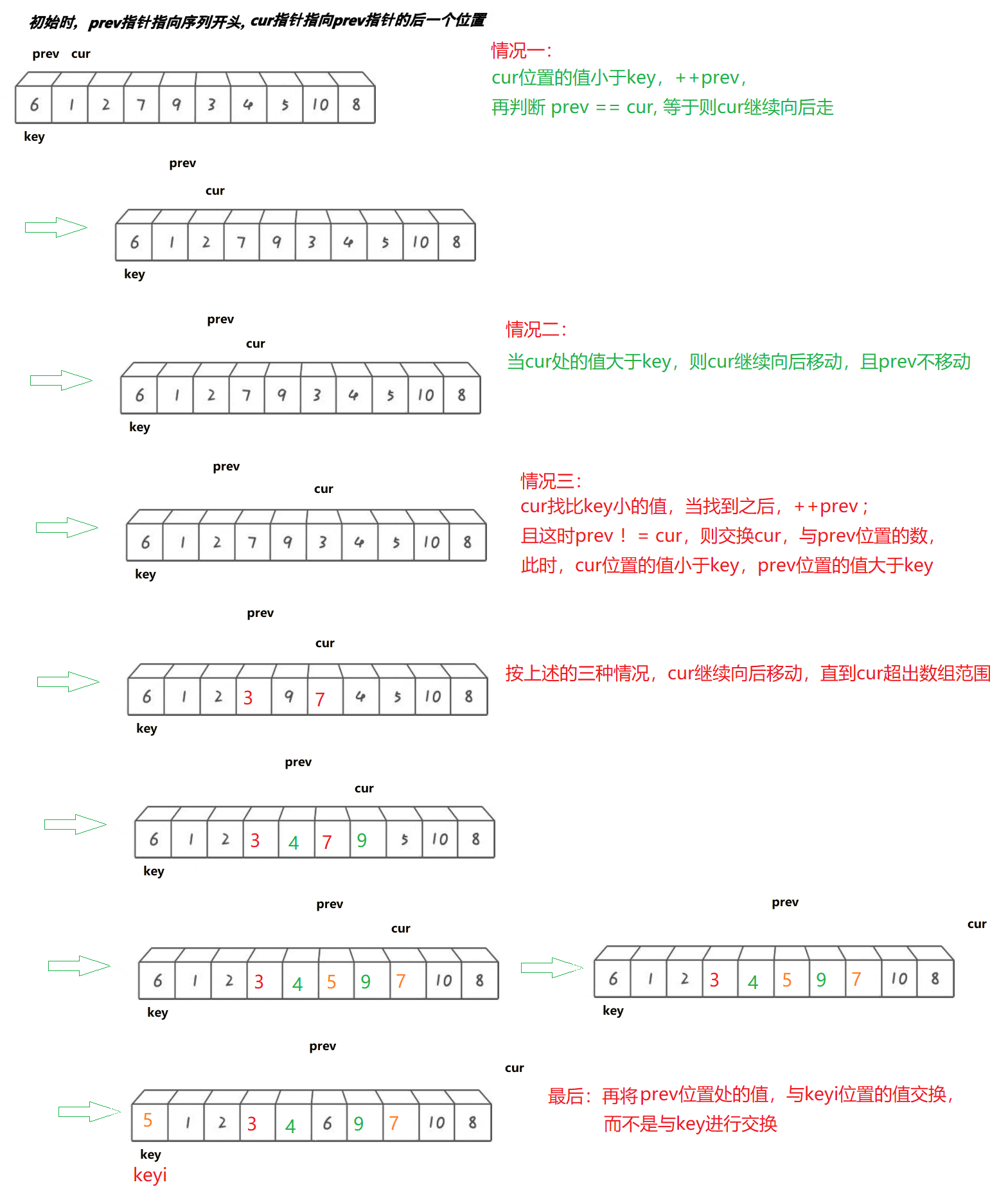
3.前后指针法
- 本质就是cur指向的值小于key,prev指向的值大于key,那么交换cur和prev所指向的值
// 三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 前后指针法
int PartSort3(int* a, int left, int right)
{// 三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){// 找小if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[keyi], &a[prev]);return prev;
}// [begin, end]
void QuickSort(int* a, int begin, int end) // 分区间递归
{if (begin >= end){return;}if (end - begin <= 8) // 8的取值,参考经验,8比较合适{InsertSort(a + begin, end - begin + 1);// 小区间优化,最后三层用插入排序}else{int keyi = PartSort3(a, begin, end);//[begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}
3.快速排序(非递归的方法)

void QuickSortNonR(int* a, int begin, int end)
{// 栈结构对象在堆上面开辟空间,不用担心栈溢出ST st; // 初始化栈StackInit(&st);// 将区间[begin,end]的左右断点存储到栈对象中StackPush(&st, begin);StackPush(&st, end);// 直到栈为空,循环结束(意味着所有的小区间都已经排序完毕了)while (!StackEmpty(&st)){// 因为压栈的时候是先压入的左端点,再压入右端点(都是下标)// 所以,从栈顶拿出数据时,是先拿出右端点,再拿出左端点(都是下标)int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);/*if (left >= right) // 在取出时,判断区间是否满足排序要求{continue;}*/// 根据拿出的区间断点,对这个区间的数据进行一趟排序int keyi = PartSort3(a, left, right);// 排序完之后,得到下标keyi,根据下标keyi将之前的区间重新分为两个新区间// 再将两个新区间的左右端点入栈,就可以重复上述的操作,完成所有区间的排序// [left, keyi-1] keyi [keyi+1,right]// 在存入时,判断区间是否满足存入要求,避免无效存储,和取出判断if (keyi + 1 < right) {StackPush(&st, keyi + 1);StackPush(&st, right);}// 在存入时,判断区间是否满足存入要求,避免无效存储,和取出判断if (left < keyi- 1) {StackPush(&st, left);StackPush(&st, keyi - 1);}}// 最后,销毁栈对象开辟的空间,防止内存泄漏StackDestroy(&st);
}
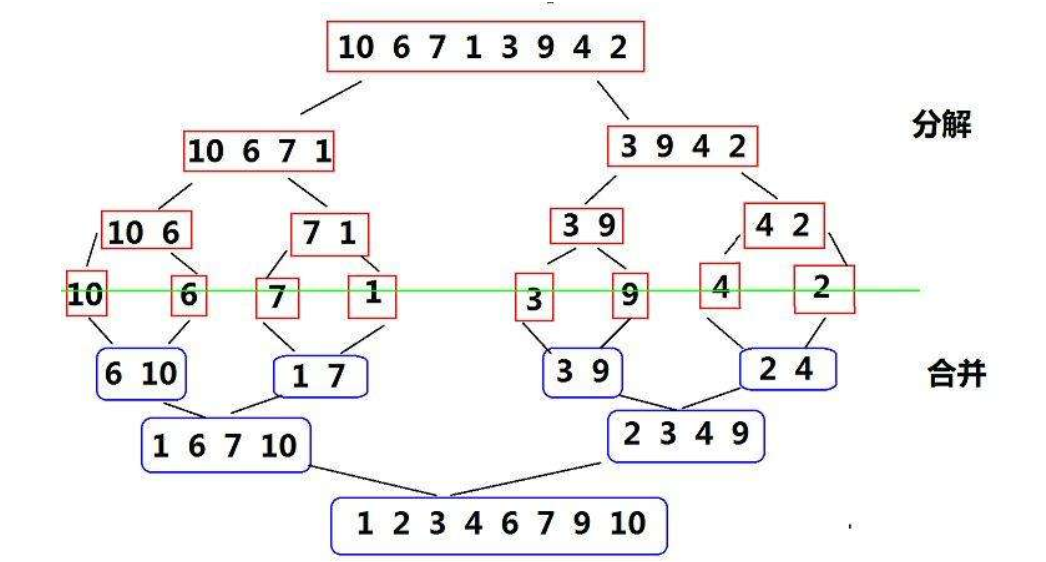
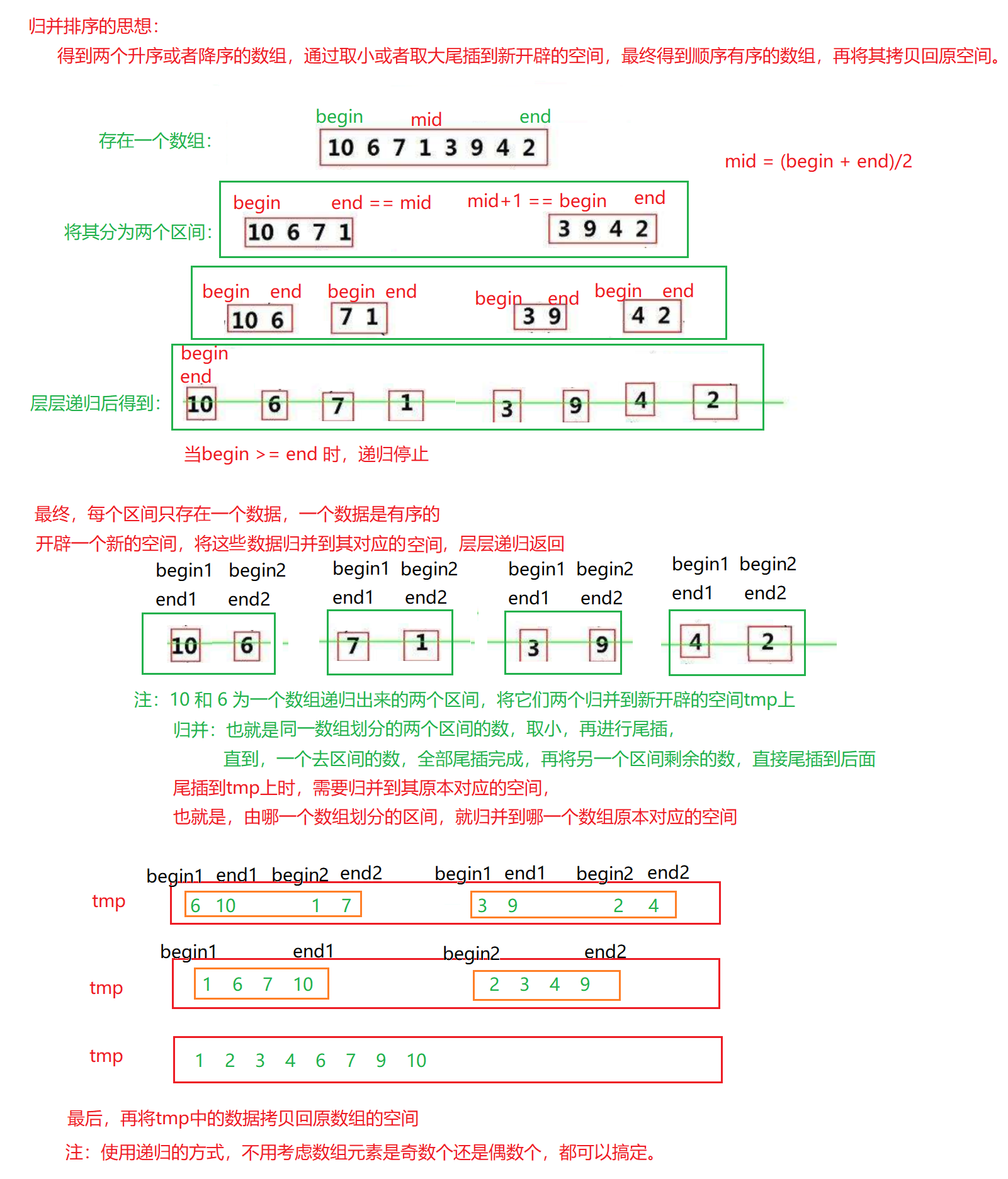
2.4 归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有
序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
归并排序(递归的方法
归并排序(递归的方法)
#define _CRT_SECURE_NO_WARNINGS#include<stdio.h>// 归并排序(递归的方法)
// 函数_MergeSort是函数MergeSort的一部分
void _MergeSort(int* a, int begin, int end, int* tmp)
{// 必须保证begin >= end为假,否则就直接返回if (begin >= end)return;// 取数组的中间下标,将数组分为两个区间int mid = (end + begin) / 2;// [begin, mid] [mid+1, end]// 左区间迭代和右区间迭代_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// 迭代完之后,此时有无数个被分裂的小区间,每个区间只有一个数// 归并 取两个区间中小的数值尾插到tmp中(tmp是一个临时数组,临时存放这些归并的数据的)// 注:因为左右区间是迭代的,所以begin,mid,end的大小对应相应的迭代,当回到迭代最初的地方// 那么[begin, mid] [mid+1, end]这两个区间的数已经是有序的了// [begin, mid] [mid+1, end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;// 两个区间的数归并时,必须满足 begin1 <= end1 && begin2 <= end2int i = begin;while (begin1 <= end1 && begin2 <= end2){// 取两个区间中较小的数尾插到tmp中if (a[begin1] <= a[begin2]){// 后置++,先使用,后++tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}// 如果区间2的数尾插完了,但是区间1的数没有尾插完,那么这里将区间一剩余的数尾插到tmp中while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}// void _MergeSort(int* a, int begin, int end, int* tmp)_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}void TestMergeSort()
{int a[] = { 100, 56, 25, 86, 99, 72, 66 };int n = sizeof(a) / sizeof(int);MergeSort(a, n);PrintArray(a, n);
}int main()
{TestMergeSort();return 0;
}
memcpy()的用法
在C语言中,memcpy() 函数用于在内存之间复制一定数量的字节。它的原型如下:
void *memcpy(void *dest, const void *src, size_t n);
dest是目标内存区域的指针,指向要复制到的位置。src是源内存区域的指针,指向要复制的数据的起始位置。n是要复制的字节数。
memcpy() 函数将源内存区域中的数据复制到目标内存区域中。它返回目标内存区域的起始位置(即 dest 指针),这使得可以将 memcpy() 作为一个表达式的一部分来使用。
以下是一个示例代码,演示了如何使用 memcpy() 函数复制内存中的数据:
#include <stdio.h>
#include <string.h>int main() {char src[] = "Hello, world!";char dest[20];// 将 src 中的数据复制到 dest 中memcpy(dest, src, strlen(src) + 1);// 打印复制后的字符串printf("Copied string: %s\n", dest);return 0;
}
在这个示例中,我们将字符串 "Hello, world!" 从源内存区域 src 复制到目标内存区域 dest 中,然后打印出复制后的字符串。
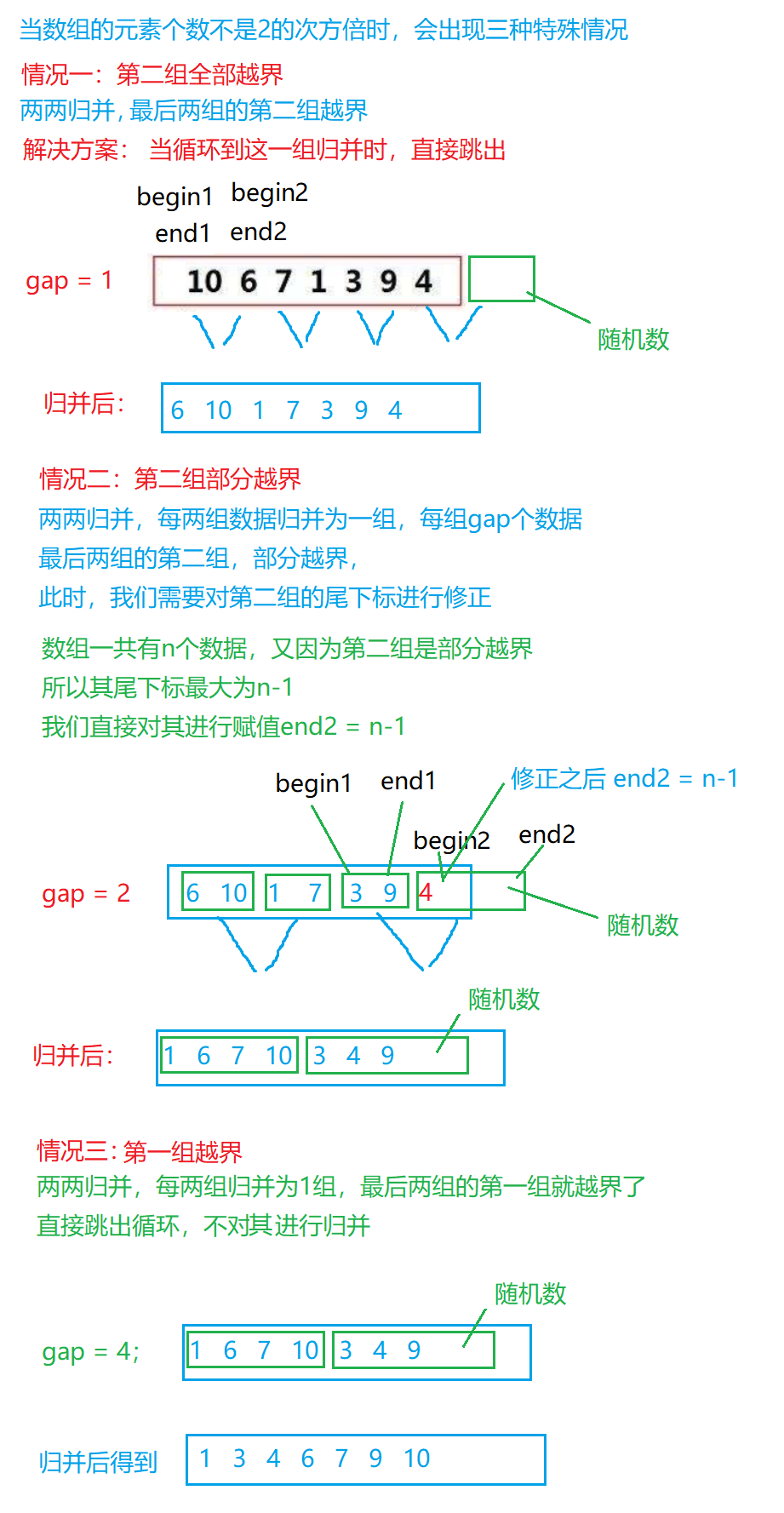
归并排序(非递归的方式)

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){// 首次循环时,每个区间只有一个数,此时gap=1// 当归并一次之后,每个区间就有两个数,那时就将gap扩大两倍// gap个数据 gap个数据归并// gap每改变一次,进行一次for循环for (int j = 0; j < n; j += 2 * gap){// 归并两个区间 取较小的值尾插到tmp// j为区间一的区间为[j,j + gap - 1]// 区间二的区间为[j + gap,j + 2 * gap - 1]int begin1 = j, end1 = j + gap - 1;int begin2 = j + gap, end2 = j + 2 * gap - 1;// 当归并到最后两组的数据,并且第一组就完全越界了// 那么不需要进行归并,直接跳出循环就可以if (end1 >= n){printf("[%d,%d]", begin1, n-1);break;}// 第二组全部越界,直接跳出循环就可以// 此时的第一组数据必然是有序的if (begin2 >= n){printf("[%d,%d]", begin1, end1);break;}// 第二组部分越界if (end2 >= n){// 修正一下end2,继续归并(第二组最后一个数的下标,最大为n-1)end2 = n - 1;}printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a+j, tmp+j, (end2-j+1)*sizeof(int));}// 扩大区间范围gap *= 2;printf("\n");}free(tmp);tmp = NULL;
}
相关文章:

8.排序(直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序)的模拟实现
1.排序的概念及其运用 1.1排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录…...
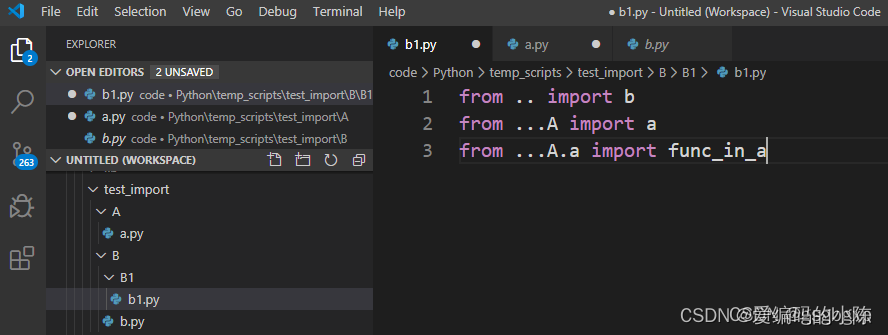
(详解)python调用另一个.py文件中的类和函数或直接运行另一个.py文件
一、同一文件夹下的调用 1.调用函数 A.py文件如下: def add(x,y):print(和为:%d%(xy))在B.py文件中调用A.py的add函数如下: import A A.add(1,2)或 from A import add add(1,2)2.调用类 A.py文件如下: class Add:def __ini…...

每日一题:修改后的最大二进制字符串
给你一个二进制字符串 binary ,它仅有 0 或者 1 组成。你可以使用下面的操作任意次对它进行修改: 操作 1 :如果二进制串包含子字符串 "00" ,你可以用 "10" 将其替换。 比方说, "00010"…...
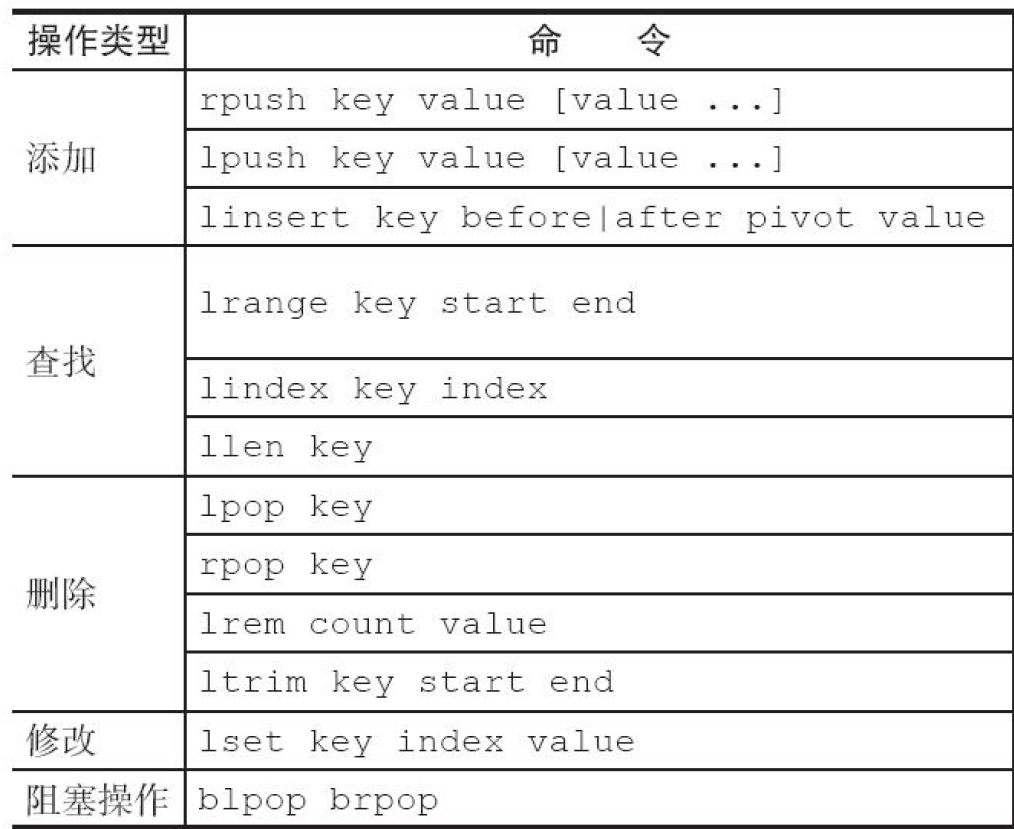
Redis 5种数据结构常用命令
文章目录 1 字符串2 哈希3 列表4 集合5 有序集合 1 字符串 命令描述set key value设置指定key的值为valueget key获取指定key的值del key [key …]删除一个或多个keymset key value [key value …]设置多个key的值mget key [key …]获取一个或多个key的值incr key将key中储存的…...

23、区间和
区间和 题目描述 假定有一个无限长的数轴,数轴上每个坐标上的数都是0。 现在,我们首先进行 n 次操作,每次操作将某一位置x上的数加c。 接下来,进行 m 次询问,每个询问包含两个整数l和r,你需要求出在区间…...
Python零基础从小白打怪升级中~~~~~~~文件和文件夹的操作 (1)
第七节:文件和文件夹的操作 一、IO流(Stream) 通过“流”的形式允许计算机程序使用相同的方式来访问不同的输入/输出源。stream是从起源(source)到接收的(sink)的有序数据。我们这里把输入/输…...
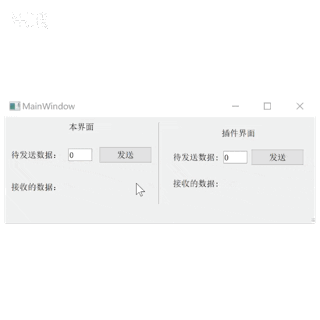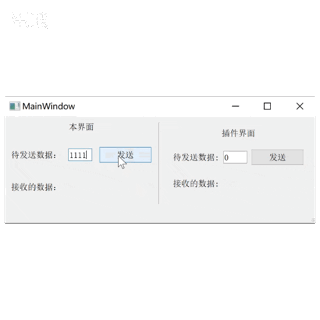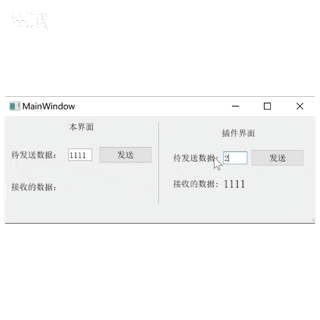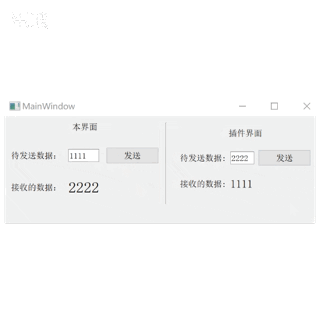
Qt plugin 开发UI界面插件
目录 1.创建接口 2.创建插件 3.创建插件界面 4.插件实现 5.创建应用工程 6.应用插件 1.创建接口 打开QtCreater,点击左上角“文件”->新建文件或项目,在弹窗中选择C/CHeader File。 输入文件名,选好路径(可自行设置名称…...

Android查看SO库的依赖
➜ bin pwd /Users/xxx/Library/Android/sdk/ndk/21.1.6352462/toolchains/aarch64-linux-android-4.9/prebuilt/darwin-x86_64/bin ➜ bin ./aarch64-linux-android-readelf -d /Download/libxxx.so 0x0000000000000001 (NEEDED) Shared library: [liblog.so]0x…...
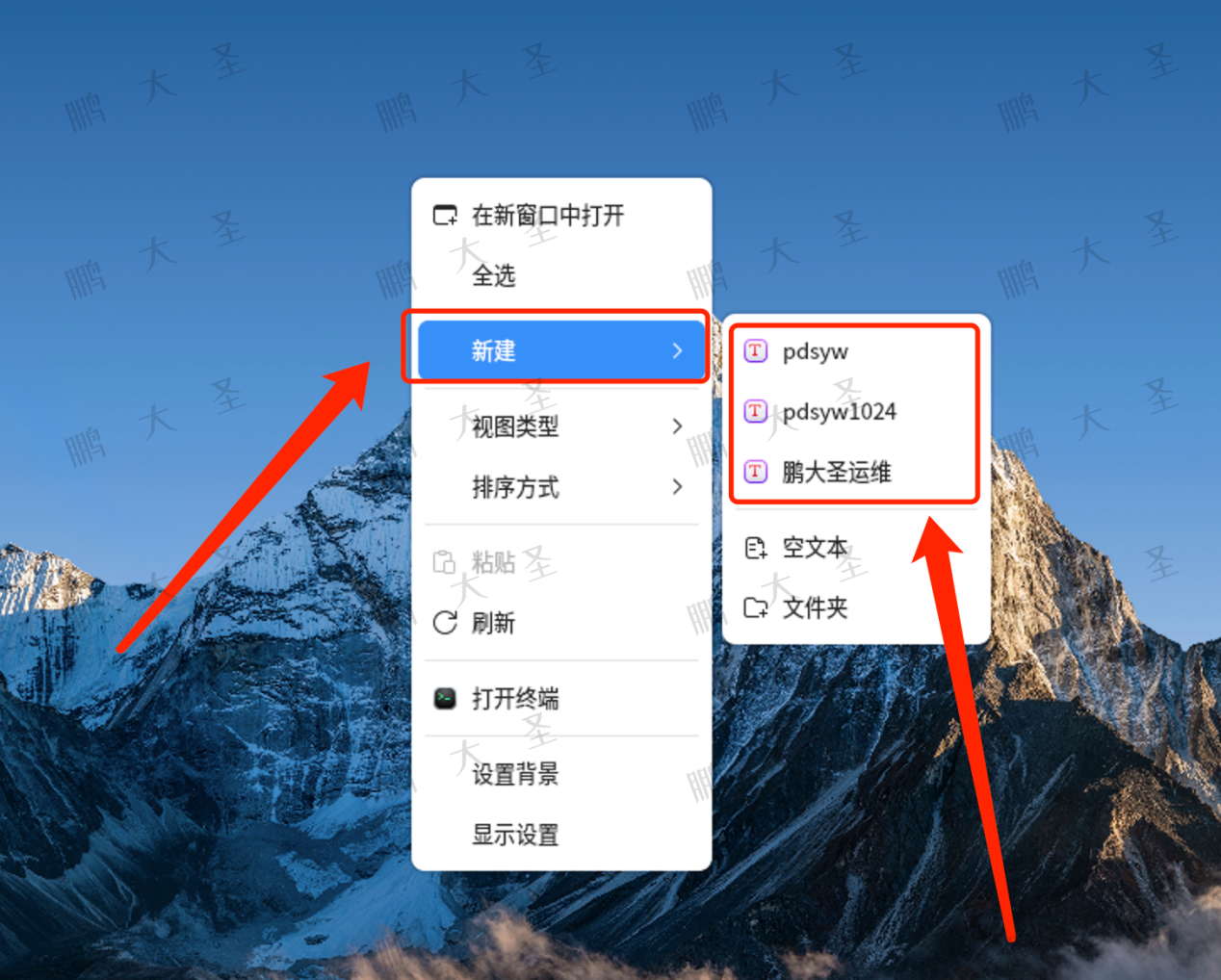
麒麟KOS删除鼠标右键新建菜单里不需要的选项
原文链接:麒麟KOS删除鼠标右键新建菜单里不需要的选项 Hello,大家好啊!在日常使用麒麟KOS操作系统时,我们可能会发现鼠标右键新建菜单里包含了一些不常用或者不需要的选项。这不仅影响我们的使用效率,也让菜单显得杂乱…...

DPDK系列之四十二DPDK应用网络编程UDP编程
一、UDP编程 UDP编程的应用和TCP编程的应用同样非常广泛,如果说真得想使用UDP编程,一般情况下还真得不至于运用DPDK这种重量级的框架。但一个框架的优秀与否,不仅仅在于自身的整体设计优秀,更重要的在于其对应用的支持更完善。 正…...

金三银四面试题(十九):MySQL中的锁
在MySQL中,锁是非常重要的,特别是在多用户并发访问数据库的环境中,因此也是面试中常问的话题。 请说说数据库的锁? 关于MySQL 的锁机制,可能会问很多问题,不过这也得看面试官在这方面的知识储备。 MySQL …...
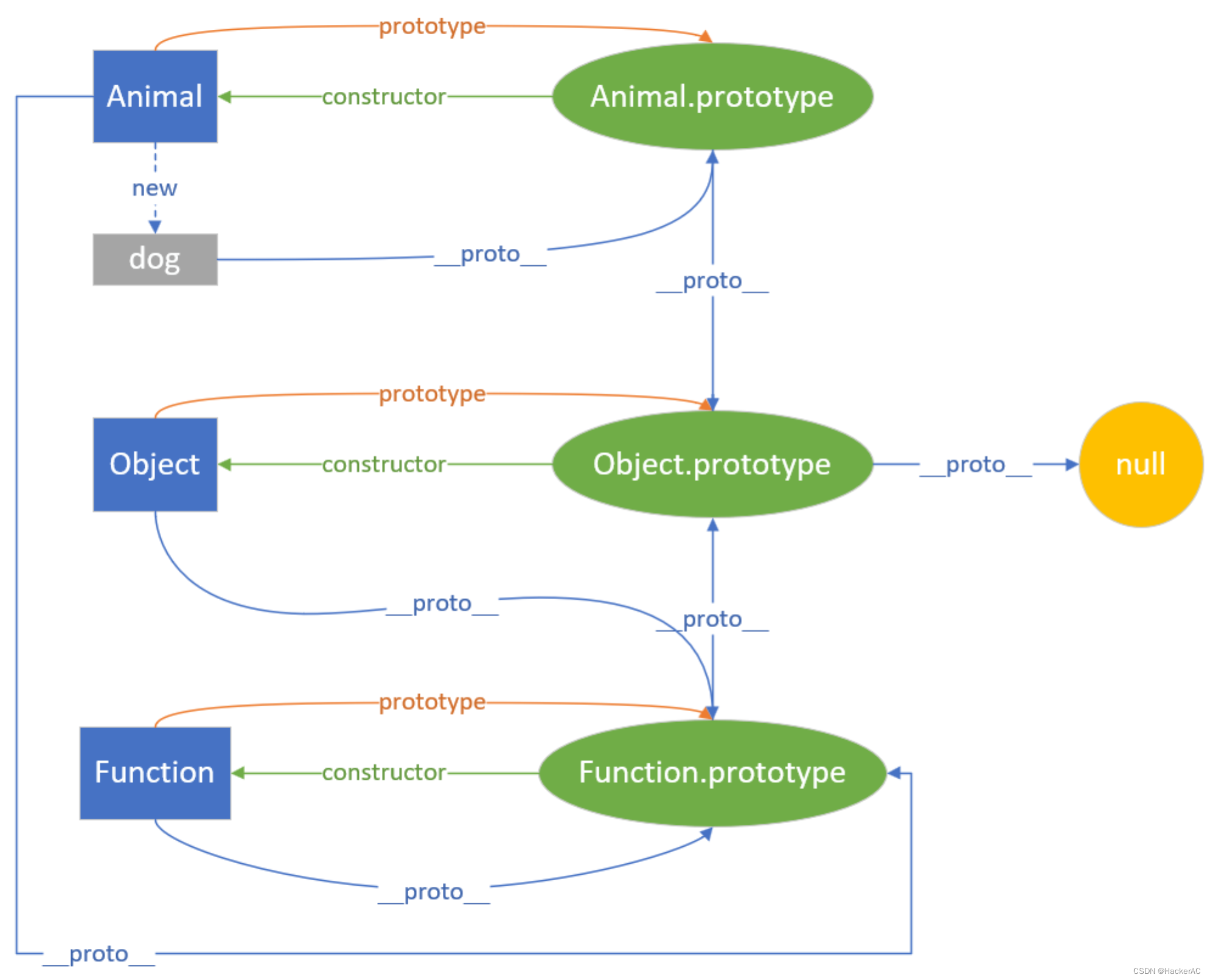
【JavaScript】原型链/作用域/this指针/闭包
1.原型链 参考资料:Annotated ES5 ECMAScript起初并不支持如C、Smalltalk 或 Java 中“类”的形式创建对象,而是通过字面量表示法或者构造函数创建对象。每个构造函数都是一个具有名为“prototype”的属性的函数,该属性用于实现基于原型的继…...

Python的MATLAB使用
Python和MATLAB是两种不同的编程语言,它们各自拥有不同的生态系统和库。然而,你可以在Python中使用一些方法来实现与MATLAB类似的功能。以下是一些方法和库,可以帮助你在Python中实现MATLAB风格的编程: 1. NumPy: NumPy是Python中…...
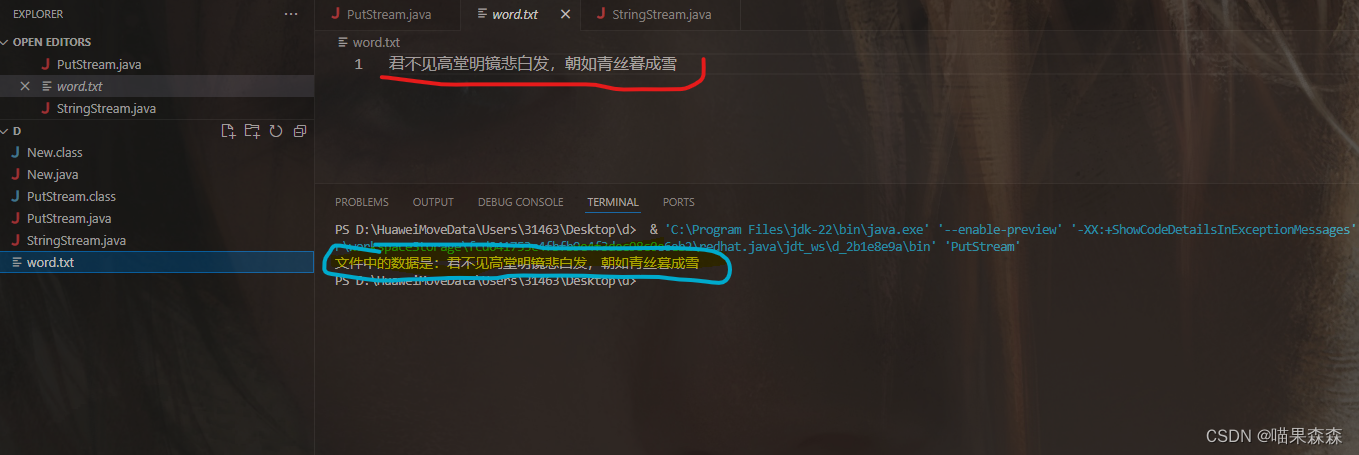
文件输入/输出流(I/O)
文章目录 前言一、文件输入\输出流是什么?二、使用方法 1.FileInputStream与FileOutputStream类2.FileReader与FileWriter类总结 前言 对于文章I/O(输入/输出流的概述),有了下文。这篇文章将具体详细展述如何向磁盘文件中输入数据,或者读取磁…...

docker,schedule job和environment variables三者的含义与区别
这三个概念在软件开发和部署中扮演着不同的角色: Docker一般长这样:superlifestyle/sscp-api Schedule Job一般长这样:recorrect_ocr_receipt_status 、Sync2D365 Environment Variables一般长这样:D365_BATCH_OPERATION_SIZE ima…...

90天玩转Python—16—基础知识篇:面向对象知识详解
90天玩转Python系列文章目录 90天玩转Python—01—基础知识篇:C站最全Python标准库总结 90天玩转Python--02--基础知识篇:初识Python与PyCharm 90天玩转Python—03—基础知识篇:Python和PyCharm(语言特点、学习方法、工具安装) 90天玩转Python—04—基础知识篇:Pytho…...

python 标准库之openpyxl的常规操作
目录 openpyxl(Excel文件处理模块) 读sheet 读sheet中单元格 合并单元格 openpyxl模块基本用法 安装方法 基本使用 读取Excel文档 (一)获取工作表 (二)获取单元格 (三)获取…...

90天玩转Python—12—基础知识篇:Python自动化操作Email:发送邮件、收邮件与邮箱客户端操作全解析
90天玩转Python系列文章目录 90天玩转Python—01—基础知识篇:C站最全Python标准库总结 90天玩转Python--02--基础知识篇:初识Python与PyCharm 90天玩转Python—03—基础知识篇:Python和PyCharm(语言特点、学习方法、工具安装) 90天玩转Python—04—基础知识篇:Pytho…...
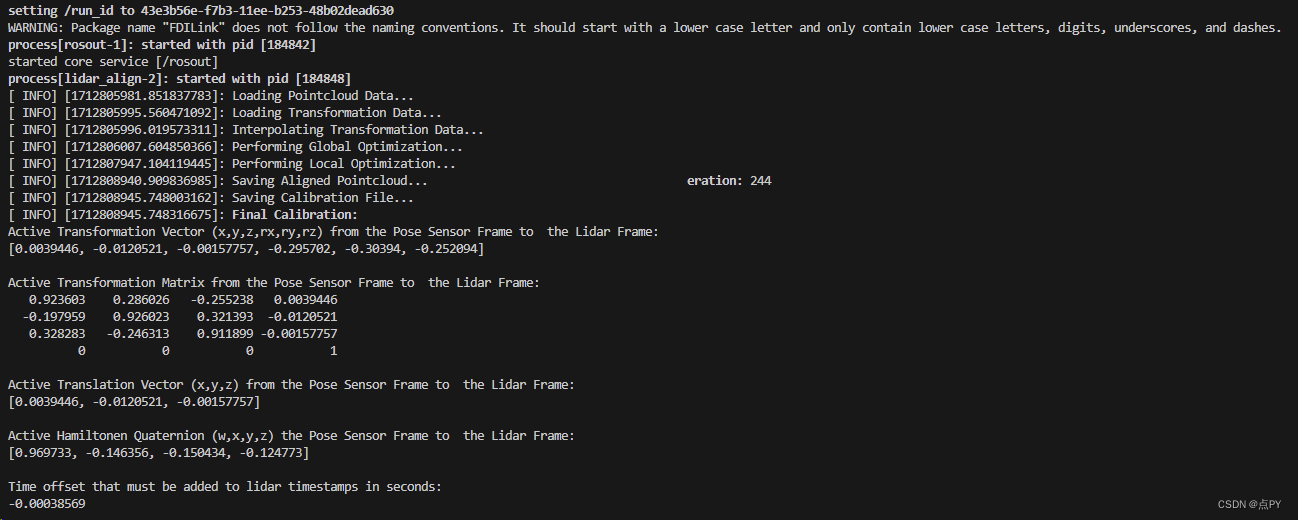
利用lidar_align来进行lidar和imu标定
文章目录 下载并安装lidar_align安装nlopt迁移NLOPTConfig.cmake修改loader.cpp文件编译并运行 下载并安装lidar_align mkdir -p lidar_align/src cd lidar_align/src git clone https://github.com/ethz-asl/lidar_align.git安装nlopt git clone http://github.com/steven…...

牛客NC93 设计LRU缓存结构【hard 链表,Map Java】
题目 题目链接: https://www.nowcoder.com/practice/5dfded165916435d9defb053c63f1e84 思路 双向链表map最新的数据放头结点,尾节点放最老的数据,没次移除尾巴节点本地考察链表的新增,删除,移动节点参考答案Java im…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
