力扣爆刷第116天之CodeTop100五连刷66-70
力扣爆刷第116天之CodeTop100五连刷66-70
文章目录
- 力扣爆刷第116天之CodeTop100五连刷66-70
- 一、144. 二叉树的前序遍历
- 二、543. 二叉树的直径
- 三、98. 验证二叉搜索树
- 四、470. 用 Rand7() 实现 Rand10()
- 五、64. 最小路径和
一、144. 二叉树的前序遍历
题目链接:https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
思路:前序遍历什么可以说的,在进入左右子树前收集节点。
class Solution {List<Integer> list = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root == null) return list;list.add(root.val);preorderTraversal(root.left);preorderTraversal(root.right);return list;}
}
二、543. 二叉树的直径
题目链接:https://leetcode.cn/problems/diameter-of-binary-tree/description/
思路:求直径其实就是求某个节点的左子树深度与右子树深度,连接成的一个向上的尖括号,理解了这个关系,就直接像求深度一样,后序遍历,求左右子树深度,记录最大值即可。
class Solution {int max = -1;public int diameterOfBinaryTree(TreeNode root) {traverse(root);return max;}int traverse(TreeNode root) {if(root == null) return 0;int left = traverse(root.left);int right = traverse(root.right);max = Math.max(max, left + right);return Math.max(left, right) + 1;}
}
三、98. 验证二叉搜索树
题目链接:https://leetcode.cn/problems/validate-binary-search-tree/description/
思路:直接中序遍历,用一个变量记录前一个节点,然后中序遍历比较,如果不是,直接早停返回。
class Solution {boolean flag = true;TreeNode pro = null;public boolean isValidBST(TreeNode root) {traverse(root);return flag;}void traverse(TreeNode root) {if(root == null || !flag) return;traverse(root.left);if(pro != null) {if(pro.val >= root.val) {flag = false;return;} }pro = root;traverse(root.right);}
}
四、470. 用 Rand7() 实现 Rand10()
题目链接:https://leetcode.cn/problems/implement-rand10-using-rand7/description/
思路:可以采用概率组合,我们可以先用rand7构造出来一个p=0.2,再构造出来一个p=0.5,这两个事件构成一个事件的概率为p=0.1正好可以达到要求,例如先随机出来一个1-6的数,奇数偶数出现的概率为0.5,范围只要是偶数就行,然后我们再随机出来一个1-5的数,因为我们只放出来1-5,就相当于袋子里只有5个数,那每种数出现的概率就为0.2,然后组合到一块,判断第一个数是奇数还是偶数,通过这个返回1-5或者6-10。就相当于0.5*0.2;
class Solution extends SolBase {public int rand10() {int first, second;while((first = rand7()) > 6) ;while((second = rand7()) > 5) ;return (first & 1) == 1 ? second : 5 + second;}
}
五、64. 最小路径和
题目链接:https://leetcode.cn/problems/minimum-path-sum/description/
思路:定义dp[i][j]表示抵达grid[i][j]时的最短路径,由于只能从上和左的方向推出,则dp[i][j]=grid[i][j]+dp[i-1][j-1],如果要压缩到一维,也是可以的,注意初始化。
class Solution {public int minPathSum(int[][] grid) {int m = grid.length, n = grid[0].length;int[] dp = new int[n+1];Arrays.fill(dp, Integer.MAX_VALUE);for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {int t = Math.min(dp[j+1], dp[j]);t = t == Integer.MAX_VALUE ? 0 : t;dp[j+1] = grid[i][j] + t;}}return dp[n];}
}相关文章:

力扣爆刷第116天之CodeTop100五连刷66-70
力扣爆刷第116天之CodeTop100五连刷66-70 文章目录 力扣爆刷第116天之CodeTop100五连刷66-70一、144. 二叉树的前序遍历二、543. 二叉树的直径三、98. 验证二叉搜索树四、470. 用 Rand7() 实现 Rand10()五、64. 最小路径和 一、144. 二叉树的前序遍历 题目链接:htt…...

B站广告推广操作教程及费用?
哔哩哔哩(B站)作为国内极具影响力的年轻人文化社区,已成为众多品牌与企业触达目标受众、提升品牌影响力的重要阵地。然而,面对B站复杂的广告系统与精细化运营需求,许多广告主可能对如何高效开展B站广告推广感到困惑。云…...

Linux操作系统之docker基础
目录 一、docker 1.1 简介 1.2 安装配置docker 二、dockerfile 1.1、简介 1.2、dockerfile 关键字 一、docker 1.1 简介 容器技术 容器其实就是虚拟机,每个容器可以运行不同的系统【系统是以linux为主的】 为什么要使用docker? docker容器之间相互隔…...

35-3 使用dnslog探测fastjson漏洞
一、DNSLog 原理 DNSLog是一种记录在DNS上的域名相关信息的机制,类似于日志文件,记录了对域名或IP的访问信息。了解多级域名的概念对理解DNSLog至关重要。因特网采用树状结构的命名方法,按照组织结构划分域,每个域都是名字空间中被管理的一个划分,可以进一步划分为子域。域…...

Qt——示波器/图表 QCustomPlot
一、介绍 QCustomPlot是一个用于绘图和数据可视化的Qt C小部件。它没有进一步的依赖关系,提供友好的文档帮助。这个绘图库专注于制作好看的,出版质量的2D绘图,图形和图表,以及为实时可视化应用程序提供高性能。QCustomPlot可以导出…...
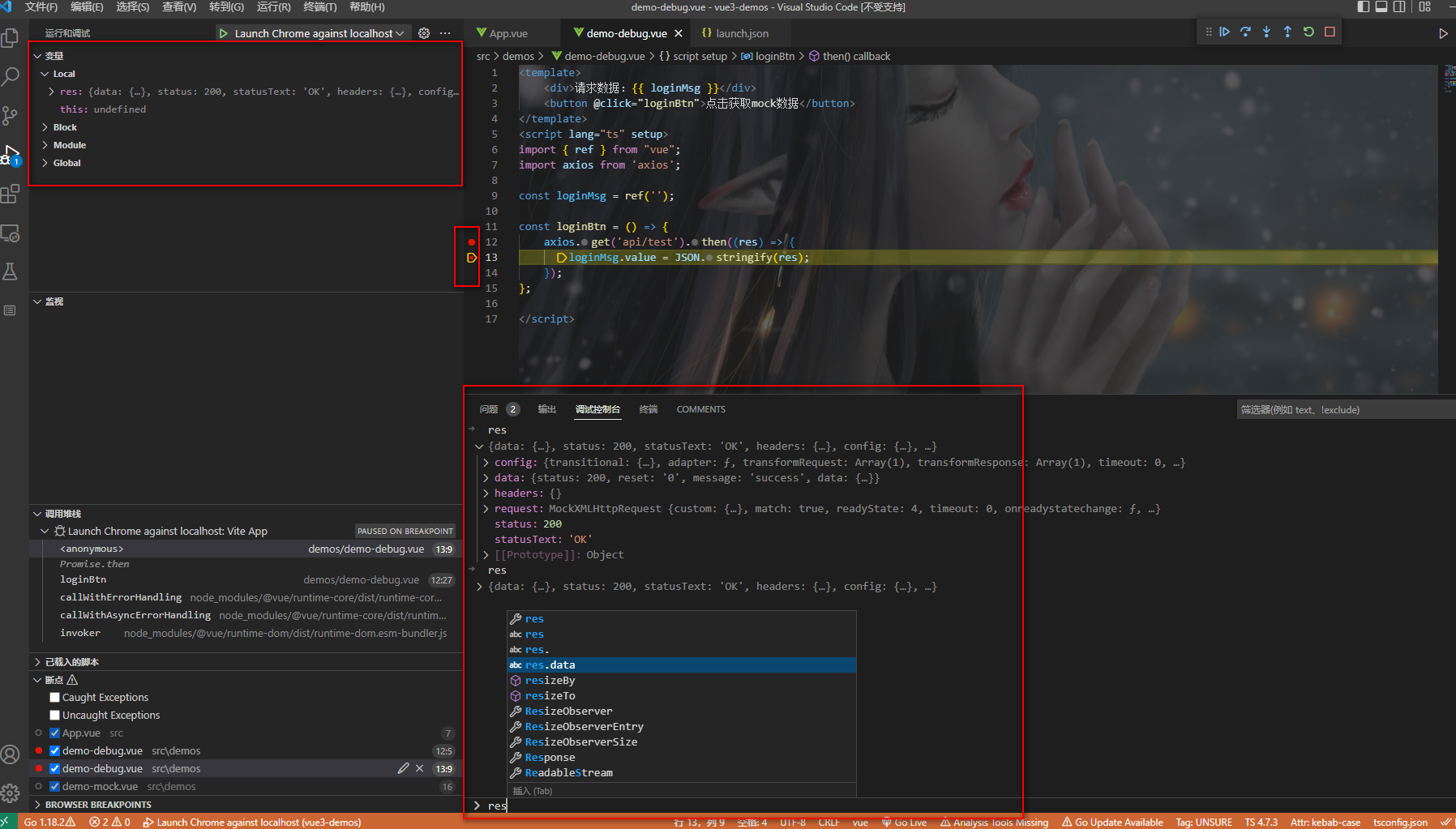
《图解Vue3.0》- 调试
如何对vue3项目进行调试 调试是开发过程中必备的一项技能,掌握了这项技能,可以很好的定义bug所在。一般在开发vue3项目时,有三种方式。 代码中添加debugger;使用浏览器调试:sourcemap需启用vs code 调试:先开启node服…...
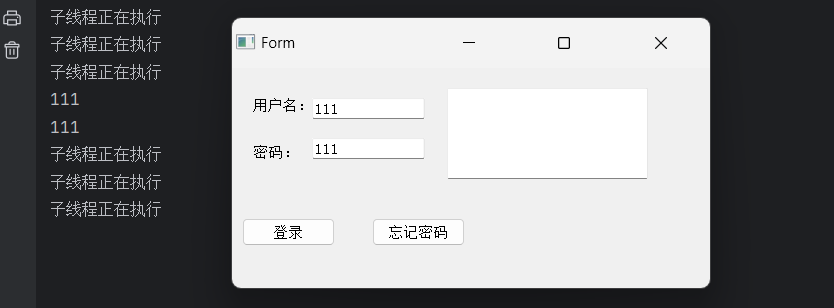
【PyQt5篇】和子线程进行通信
文章目录 🍔使用QtDesigner进行设计🛸和子线程进行通信🎈运行结果 🍔使用QtDesigner进行设计 我们首先使用QtDesigner设计界面 得到代码login.ui <?xml version"1.0" encoding"UTF-8"?> <ui …...

JavaScript数组操作方法全录
改变原数组的方法: push() - 将一个或多个元素添加到数组的末尾,并返回新数组的长度。 pop() - 从数组中移除最后一个元素,并返回该元素。 shift() - 从数组中移除第一个元素,并返回该元素。 unshift() - 将一个或多个元素添加到…...
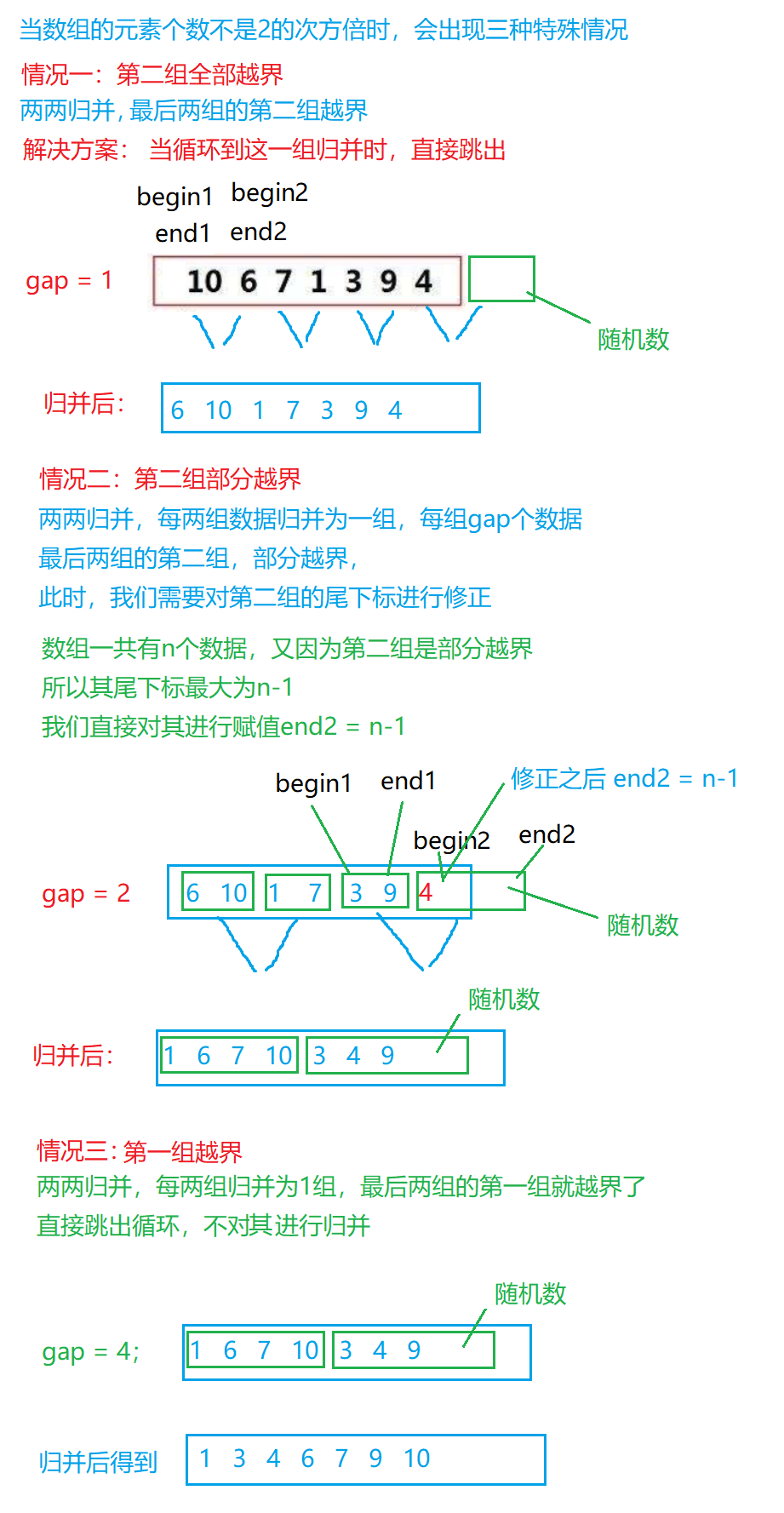
8.排序(直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序)的模拟实现
1.排序的概念及其运用 1.1排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录…...
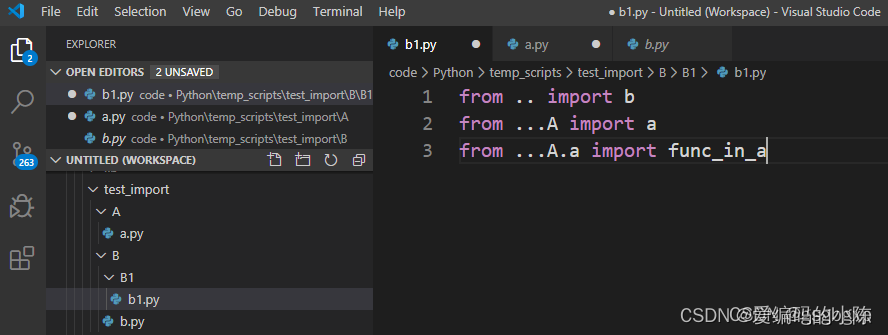
(详解)python调用另一个.py文件中的类和函数或直接运行另一个.py文件
一、同一文件夹下的调用 1.调用函数 A.py文件如下: def add(x,y):print(和为:%d%(xy))在B.py文件中调用A.py的add函数如下: import A A.add(1,2)或 from A import add add(1,2)2.调用类 A.py文件如下: class Add:def __ini…...

每日一题:修改后的最大二进制字符串
给你一个二进制字符串 binary ,它仅有 0 或者 1 组成。你可以使用下面的操作任意次对它进行修改: 操作 1 :如果二进制串包含子字符串 "00" ,你可以用 "10" 将其替换。 比方说, "00010"…...
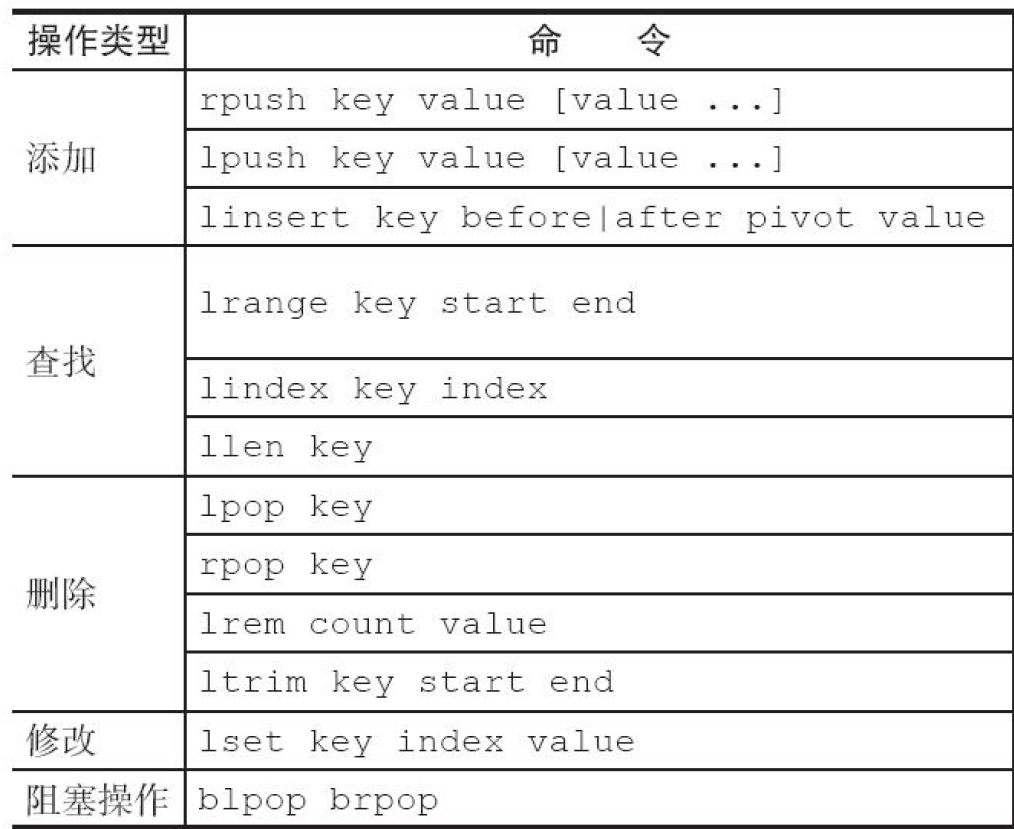
Redis 5种数据结构常用命令
文章目录 1 字符串2 哈希3 列表4 集合5 有序集合 1 字符串 命令描述set key value设置指定key的值为valueget key获取指定key的值del key [key …]删除一个或多个keymset key value [key value …]设置多个key的值mget key [key …]获取一个或多个key的值incr key将key中储存的…...

23、区间和
区间和 题目描述 假定有一个无限长的数轴,数轴上每个坐标上的数都是0。 现在,我们首先进行 n 次操作,每次操作将某一位置x上的数加c。 接下来,进行 m 次询问,每个询问包含两个整数l和r,你需要求出在区间…...
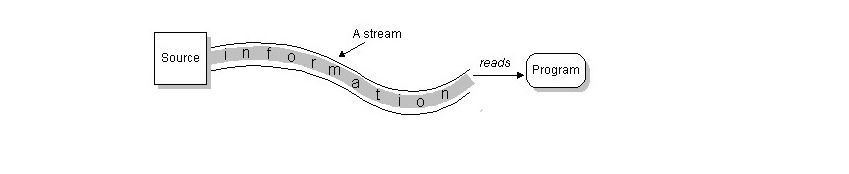
Python零基础从小白打怪升级中~~~~~~~文件和文件夹的操作 (1)
第七节:文件和文件夹的操作 一、IO流(Stream) 通过“流”的形式允许计算机程序使用相同的方式来访问不同的输入/输出源。stream是从起源(source)到接收的(sink)的有序数据。我们这里把输入/输…...
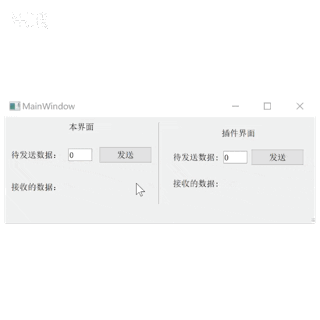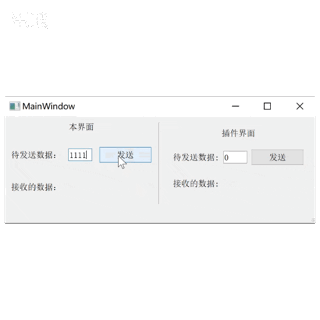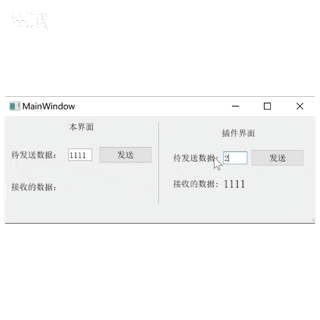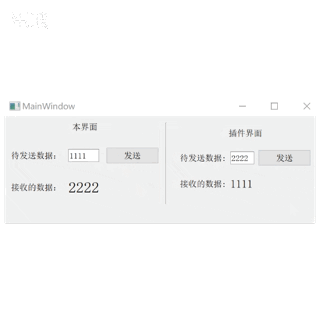
Qt plugin 开发UI界面插件
目录 1.创建接口 2.创建插件 3.创建插件界面 4.插件实现 5.创建应用工程 6.应用插件 1.创建接口 打开QtCreater,点击左上角“文件”->新建文件或项目,在弹窗中选择C/CHeader File。 输入文件名,选好路径(可自行设置名称…...

Android查看SO库的依赖
➜ bin pwd /Users/xxx/Library/Android/sdk/ndk/21.1.6352462/toolchains/aarch64-linux-android-4.9/prebuilt/darwin-x86_64/bin ➜ bin ./aarch64-linux-android-readelf -d /Download/libxxx.so 0x0000000000000001 (NEEDED) Shared library: [liblog.so]0x…...
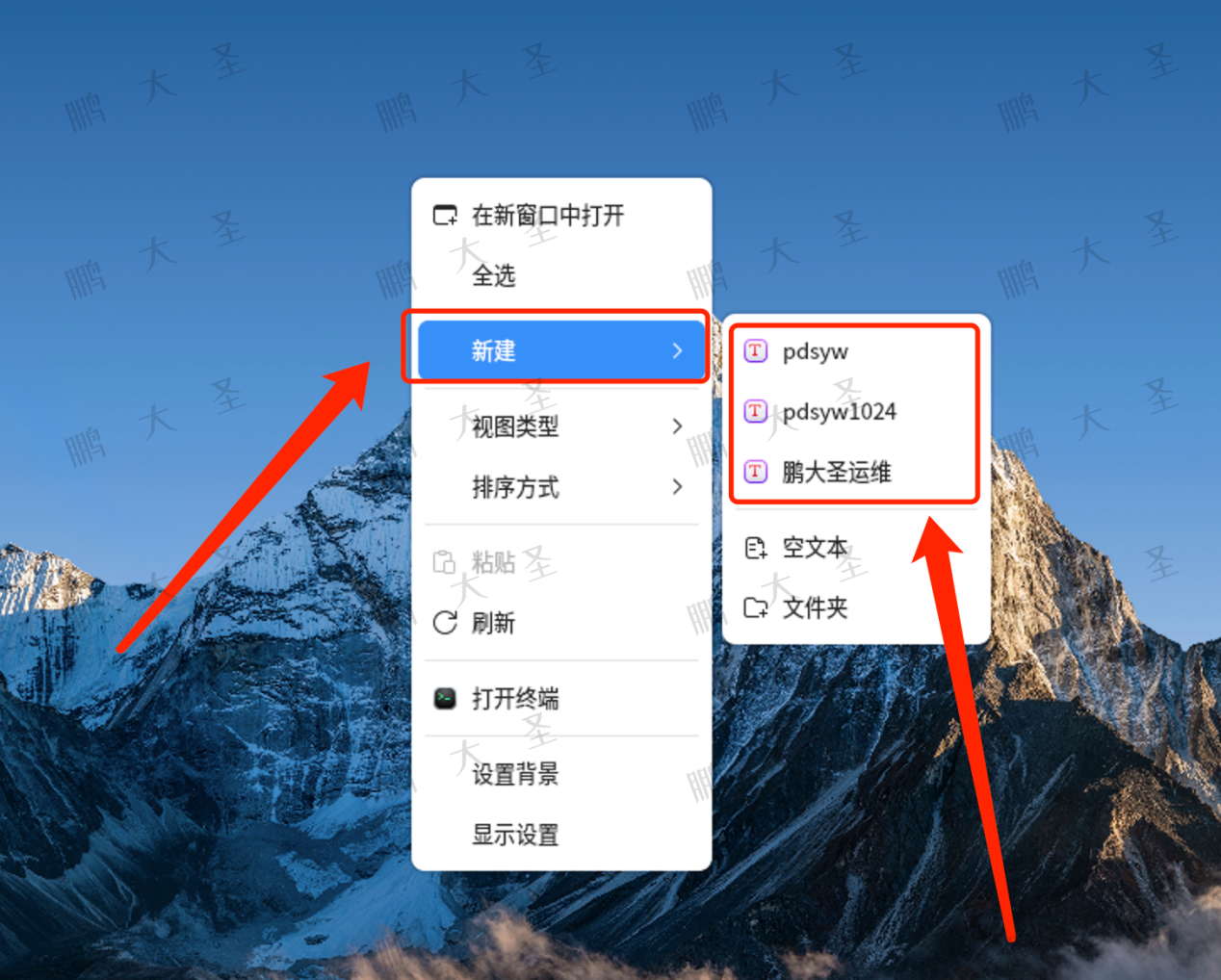
麒麟KOS删除鼠标右键新建菜单里不需要的选项
原文链接:麒麟KOS删除鼠标右键新建菜单里不需要的选项 Hello,大家好啊!在日常使用麒麟KOS操作系统时,我们可能会发现鼠标右键新建菜单里包含了一些不常用或者不需要的选项。这不仅影响我们的使用效率,也让菜单显得杂乱…...

DPDK系列之四十二DPDK应用网络编程UDP编程
一、UDP编程 UDP编程的应用和TCP编程的应用同样非常广泛,如果说真得想使用UDP编程,一般情况下还真得不至于运用DPDK这种重量级的框架。但一个框架的优秀与否,不仅仅在于自身的整体设计优秀,更重要的在于其对应用的支持更完善。 正…...

金三银四面试题(十九):MySQL中的锁
在MySQL中,锁是非常重要的,特别是在多用户并发访问数据库的环境中,因此也是面试中常问的话题。 请说说数据库的锁? 关于MySQL 的锁机制,可能会问很多问题,不过这也得看面试官在这方面的知识储备。 MySQL …...
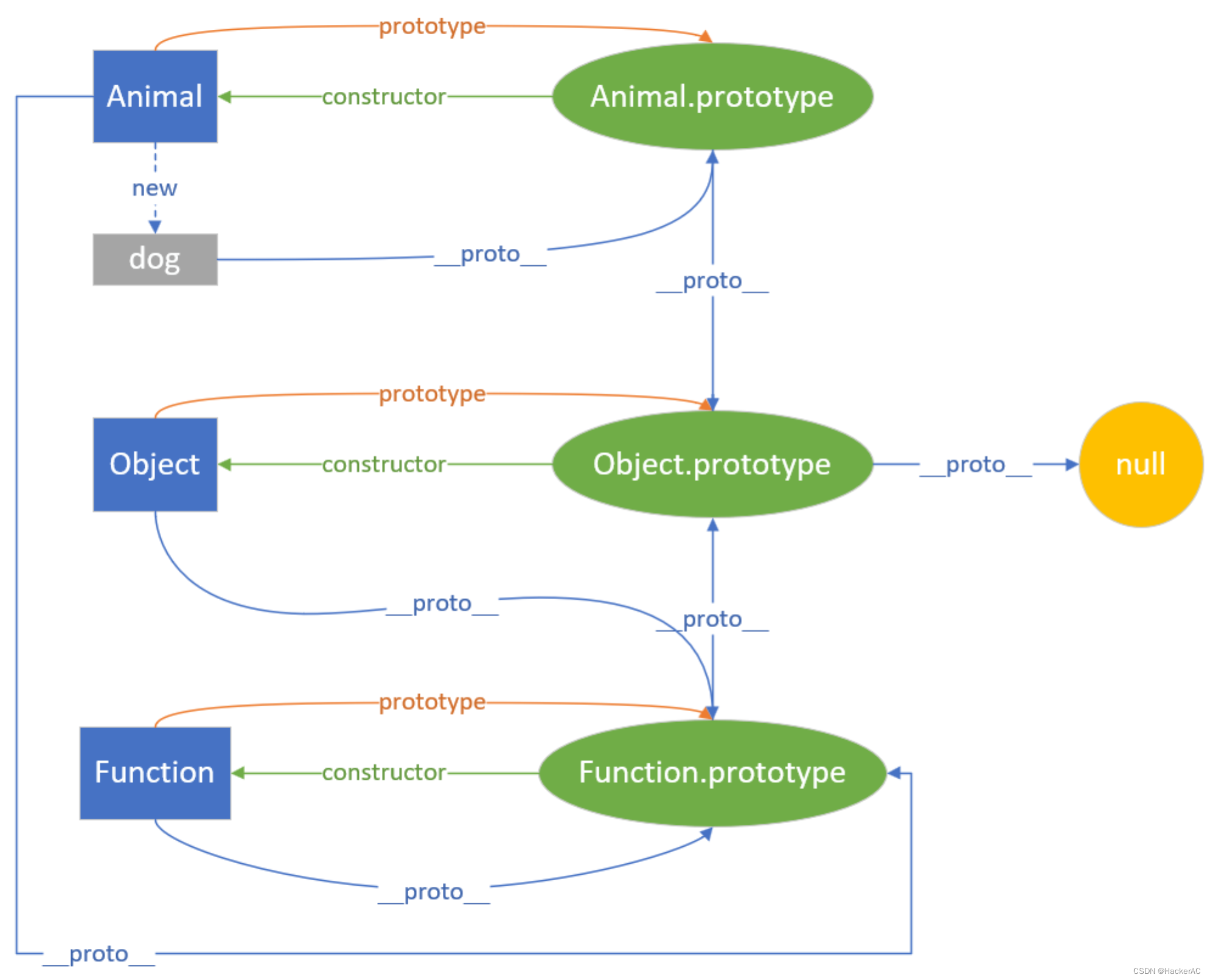
【JavaScript】原型链/作用域/this指针/闭包
1.原型链 参考资料:Annotated ES5 ECMAScript起初并不支持如C、Smalltalk 或 Java 中“类”的形式创建对象,而是通过字面量表示法或者构造函数创建对象。每个构造函数都是一个具有名为“prototype”的属性的函数,该属性用于实现基于原型的继…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
