【数据结构】初识数据结构与复杂度总结
前言
C语言这块算是总结完了,那从本篇开始就是步入一个新的大章——数据结构,这篇我们先来认识一下数据结构有关知识,以及复杂度的相关知识
个人主页:小张同学zkf
若有问题 评论区见
感兴趣就关注一下吧

目录
1.什么是数据结构
2.什么是算法?
3.算法的复杂度
3.1时间复杂度
3.2三种情况
3.3空间复杂度
1.什么是数据结构
数据结构是计算机存储,组织数据的方式,指的是相互之间存在一种或多种特定关系的数据元素的集合

2.什么是算法?
数据结构离不开算法,那算法是什么东西那,简单来说是一个定义好的计算过程。就是取一个或一组值输入,并产生出一个或一组值作为输出,当中产生的的计算步骤,用来将输入数据转化成输出结果

3.算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度
时间复杂度主要衡量一个算法的快慢,而空间复杂度主要衡量一个算法运行的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎,但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度,所以我们如今已经不需要在特别关注一个算法的空间复杂度。
3.1时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数(注:这里的函数是数学上的函数,不是c语言的函数!!!),它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序跑起来,才能知道,但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方法。一个算法所花费的的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。

//请计算一下Func1中++count语句总共执行了多少次?
void Funcl(int N)
{
int count =0;
for(int i=0;i<N;++i)
{
for(int j=0;j<N;++j)
{
++count;
}
}for (int k=0;k<2*N;++k)
{
++count;
}
int M=10;
while(M--)
{
++count;
}
printf("%d\n",count);
}
上面的时间复杂度是多少
我们用数学函数来表示,来看第一个函数,两个for循环,那执行次数是不是就是N的平方次,再看第二个函数执行2N次,最后一个函数执行10次
那就是F(N)=N^2+2*N+10
精算值 估算值
N=10 F(N)=130 100
N=100 F(N)=10210 10000
N=1000 F(N)=1002010 1000000
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法
那么要求大概值,哪个表达式对次数影响最大呢,是不是N^2 最大,我么可以这样想一下,如果N越来越大,后面俩表达式2*N和10是不是对时间复杂度影响越来越小,我们取极限,那后面俩就没影响,只有N^2对次数影响特别大,所以只保留这一项,我们也可以从这里看出来,若为多项式,我们只取次数高的那一项
那么这个函数的时间复杂度为O(N^2) 这也就是大O的渐进表示法
那我们再来看一个例子,巩固一下
//计算Func3的时间复杂度?
void Func3(int N,int M)
{
int count =0;
for (int k=0;k<M;++k)
{
++count;
}
}
for (int k=0;k<N;++k)
{
++count;
}
printf("%d\n",count);我们还是先用函数表示 F(N)=N+M
这下就有疑问了,那这个用大O怎么表示

我们可以看一下,这里没有明确说明N远大于M还是M远大于N,都没有明确说明,那就是对执行次数影响是同等的,谁都不能舍去,所以结果为O(N)=N+M
我们再来看一个
//计算Func4的时间复杂度?
void Func4(int N)
{
int count =0;
for (int k =0;k<100;++k)
{
++count;
}
printf("%d\n",count);
}这个时间复杂度又是多少呢
我们乍一看这次执行次数可以直接看出来,一共执行了100次
那大O怎么表示那,其实在大O里常数全部用1来表示,所以结果为O(N)=1
 一定要注意这里,这里的结果1不是执行了一次,而是代表常数次,就是我们可以看出来的次数,执行次数不是未知数的话,那运行时间就是固定的,所以它们的时间复杂度都是O(N)=1!!!!!!!
一定要注意这里,这里的结果1不是执行了一次,而是代表常数次,就是我们可以看出来的次数,执行次数不是未知数的话,那运行时间就是固定的,所以它们的时间复杂度都是O(N)=1!!!!!!!
综上,我们可得出推导大O的方法
1.用常数1取代运行时间中的所有加法常数
2.在修改后的运行次数函数中,只保留最高阶项,如果最高阶项存在且不是1,则去除与这个项目相乘的常数(也就是把系数去掉)
3.O(1)不是代表1次,是代表常数次
3.2三种情况
有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)


我们来看一下这个函数,是不是有点眼熟,没错我们之前总结过的冒泡排序,那它的时间复杂度该怎么求那,我们要求它的最坏情况,我们先想一想,冒泡排序是怎么排序的,是不是第一个数先进行挨个比较,然后是第二个数字,以此类推,那我们第一个数字是不是要比较N-1次,第二个数字就是N-2次……直到最后比较一次,那把这些都加起来是不是就是我们的时间复杂度了,那就是求等差数列的和,函数为N*(N-1)/2,大O表示法取最高项结果为O(N^2)
我们继续看一个
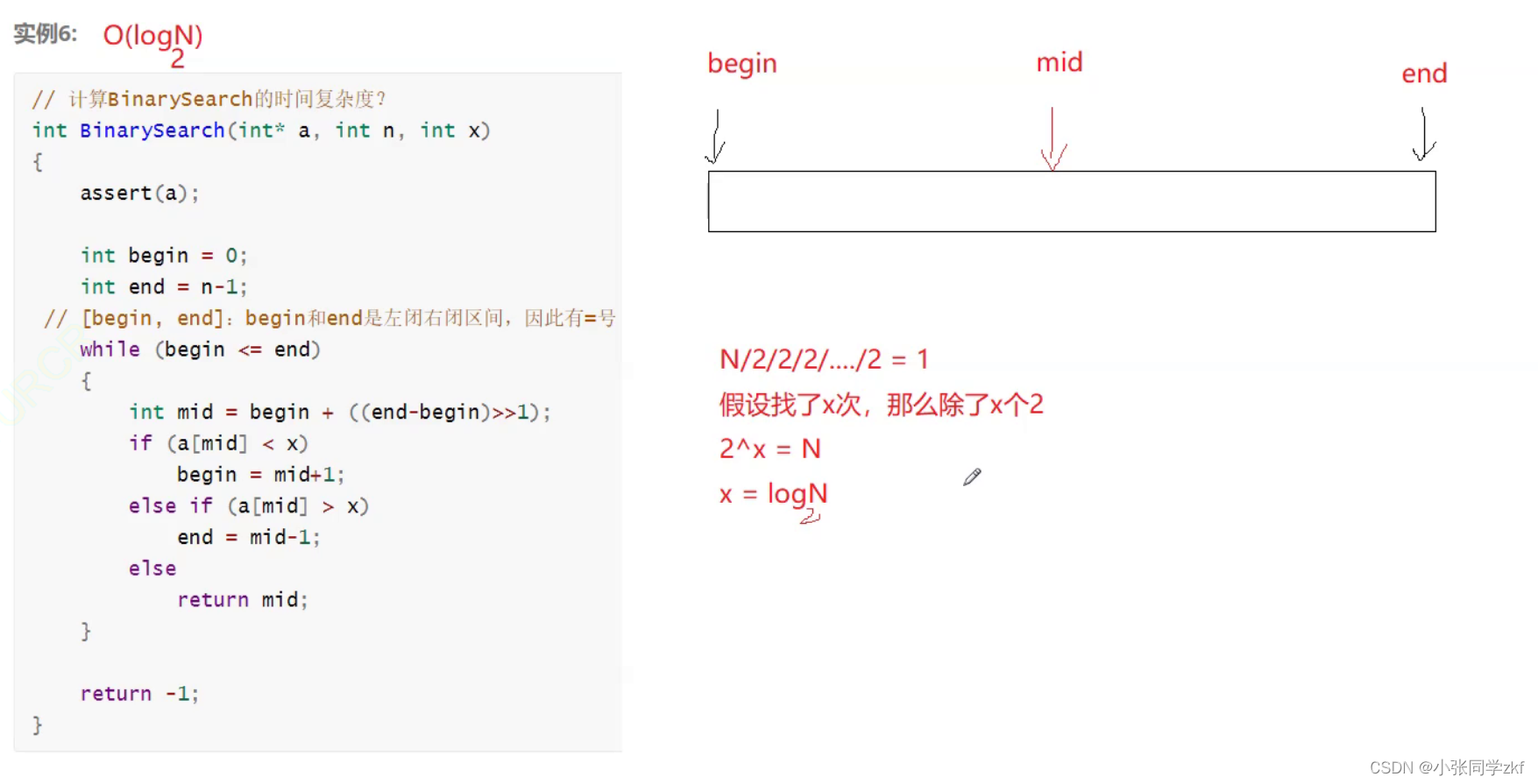
这个是不是也是有点眼熟,对我之前总结的猜数字游戏里的二分查找,那它的时间复杂度是多少那,我们先来想一想这个函数怎么实现的,是每次查找缩小一半范围,相当于除2,查找一次除一次2,那N次就是除N个2,那时间复杂度不就是除2的次数嘛,那不就是log2N嘛,用大O表示就是O(N)=log2N
我们再来看一个

还记得这个吧,没错这个也是我之前总结的递归问题中的青蛙跳台阶——斐波那契数列,这个时间复杂度又是什么那
我们看一下这个函数,是不是递归一次执行一次,但它一个函数内递归了两次,那它接下来是不是像树状线一样,一个函数分两个函数,如图所示,我们来找一下规律,是不是从2^0到2^(n-2)
那把这些都加起来,就是时间复杂度了

我们可以根据错位相减法得到2^(n-1)-1,用大O表示就是O(N)=2^N
3.3空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时额外占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。


这个空间复杂度是多少
我们来看一下,这个函数开辟了一个数组空间,以及一些变量的空间,都是常数个,所以用大O表示是O(N)=1
继续看一个

这个空间复杂度是多少
这里函数运行时额外开了一个n+1的空间,这个空间就是它的空间复杂度用大O表示就是O(N)
再看一个递归

这个空间复杂度是多少
它运行时创立了N个函数栈帧,所以它的结果为O(N)
我们来看一个复杂点的

这个时间复杂度我们知道了是O(2^N)空间复杂度那
这个我们要好好想想,递归函数在创建函数栈帧的特点,第一列的函数栈帧创建完,调用完再销毁,后几列的函数递归再用第一列的曾经函数栈帧所用的空间,不会额外再开辟新的函数栈帧,简单来说就是第一列函数递归的深度就是它的空间复杂度,后面的函数递归,在第一列函数栈帧用完销毁的空间基础上,再重复利用这个空间进行第二次函数递归

我们要记住一点:空间可以重复利用!!!! ,不用累计计算
所以这个空间复杂度就是第一列函数递归开辟的空间,用大O表示O(N)
结束语
这篇博客我们对数据结构有了基础的认识,通过这篇博客,我们以后写代码要考虑这个算法的效率问题,尽量保证时间复杂度消耗低,空间复杂度空间不浪费,时间第一,空间其次的想法,研究出效率高的算法。
OK感谢观看!!!!!
相关文章:

【数据结构】初识数据结构与复杂度总结
前言 C语言这块算是总结完了,那从本篇开始就是步入一个新的大章——数据结构,这篇我们先来认识一下数据结构有关知识,以及复杂度的相关知识 个人主页:小张同学zkf 若有问题 评论区见 感兴趣就关注一下吧 目录 1.什么是数据结构 2.…...

子域名是什么?有什么作用?
在互联网世界中,域名是我们访问网站的关键。每一个公司的网站都需要拥有自己的域名,其中有些大型公司的网站还不止一个域名,除了主域名外还拥有子域名。有些人感到非常困惑,不知道子域名是什么。其实子域名也就是平时所说的二级域…...

学习 Rust 的第一天:基础知识
如果你对 Rust 一无所知,那我来解释一下。 “Rust 是一种系统编程语言,其优先考虑性能、内存安全和零成本抽象。” 你好,世界 我之前研究过 Rust,并且对 Java、C、C 和 Python 的基本编程概念有相当了解。 今天,我…...

电商技术揭秘七:搜索引擎中的SEO关键词策略与内容优化技术
文章目录 引言一、关键词策略1.1 关键词研究与选择1. 确定目标受众2. 使用关键词研究工具3. 分析搜索量和竞争程度4. 考虑长尾关键词5. 关键词的商业意图6. 创建关键词列表7. 持续监控和调整 1.2 关键词布局与密度1. 关键词自然分布2. 标题标签的使用3. 首次段落的重要性4. 关键…...
系统开发实训小组作业week7 —— 优化系统开发计划
目录 1. 建立规则,仪式,流程,模式 2. 给好行为正面的反馈 3. 明确指出不合适的行为,必要时调整人员 在 “系统开发实训课程” 中,我们小组的项目是 “电影院会员管理系统” 。在项目的开发过程中,我们遇…...
golang的引用和非引用总结
目录 概述 一、基本概念 指针类型(Pointer type) 非引用类型(值类型) 引用类型(Reference Types) 解引用(dereference) 二、引用类型和非引用类型的区别 三、golang数据类型…...

2024认证杯数学建模B题思路模型代码
目录 2024认证杯数学建模B题思路模型代码:4.11开赛后第一时间更新,获取见文末名片 第十三届“认证杯”数学中国数学建模比赛赛后体会 2024认证杯数学建模B题思路模型代码:4.11开赛后第一时间更新,获取见文末名片 第十三届“认证杯”数学中国数学建模比…...

一种快速移植 OpenHarmony Linux 内核的方法
移植概述 本文面向希望将 OpenHarmony 移植到三方芯片平台硬件的开发者,介绍一种借助三方芯片平台自带 Linux 内核的现有能力,快速移植 OpenHarmony 到三方芯片平台的方法。 移植到三方芯片平台的整体思路 内核态层和用户态层 为了更好的解释整个内核…...

java的jar包jakarta.jakartaee-web-api和jakarta.servlet-api有什么区别
jakarta.jakartaee-web-api和jakarta.servlet-api都是Java EE(现在是 Jakarta EE)中的一部分,用于开发基于Java EE平台的Web应用程序。它们之间的区别在于以下几点: 命名空间: jakarta.servlet-api是Java EE 8之前版本…...

QT_day2
使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt4版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",密码是否为…...
Advanced RAG 02:揭开 PDF 文档解析的神秘面纱
编者按: 自 2023 年以来,RAG 已成为基于 LLM 的人工智能系统中应用最为广泛的架构之一。由于诸多产品的关键功能(如:领域智能问答、知识库构建等)严重依赖RAG,优化其性能、提高检索效率和准确性迫在眉睫&am…...

Spring面试题pro版-1
Spring框架是由于软件开发的复杂性而创建的。Spring使用的是基本的JavaBean来完成以前只可能由EJB完成的事情。然而,Spring的用途不仅仅限于服务器端的开发。从简单性、可测试性和松耦合性角度而言,绝大部分Java应用都可以从Spring中受益。 Spring是什么…...

6 Reverse Linked List
分数 20 作者 陈越 单位 浙江大学 Write a nonrecursive procedure to reverse a singly linked list in O(N) time using constant extra space. Format of functions: List Reverse( List L ); where List is defined as the following: typedef struct Node *PtrToNo…...

【随笔】Git 高级篇 -- 相对引用2 HEAD~n(十三)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...

2024免费Mac电脑用户的系统清理和优化软件CleanMyMac
作为产品营销专家,对于各类产品的特性与优势有着深入的了解。CleanMyMac是一款针对Mac电脑用户的系统清理和优化软件,旨在帮助用户轻松管理、优化和保护Mac电脑。以下是关于CleanMyMac的详细介绍: CleanMyMac X2024全新版下载如下: https://…...
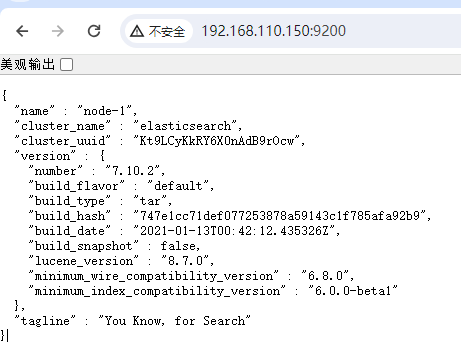
Centos7源码方式安装Elasticsearch 7.10.2单机版
版本选择参考:Elasticsearch如何选择版本-CSDN博客 下载 任选一种方式下载 官网7.10.2版本下载地址: https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-7.10.2-linux-x86_64.tar.gz 网盘下载链接 链接:https://pan…...

mysql的安装和部署
##官网下载mysql 我下载的是一个mysql-5.7.38-linux-glibc2.12-x86_64.tar.gz 可以通过xshell 或者xftp传送 xshell则是先下载一个lrzsz 执行以下的命令 yum install lrzsz -y #安装好我下面有个一键安装的脚本 #!/bin/bash#解决软件的依赖关系 yum install cmake ncurses…...

大数据基本名词
目录[-] 1.1. 1. Hadoop1.2. 2. Hive1.3. 3. Impala1.4. 4. Hbase1.5. 5.hadoop hive impala hbase关系1.6. 6. Spark1.7. 7. Flink1.8. 8. Spark 和 Flink 的应用场景 1. Hadoop 开源官网:https://hadoop.apache.org/ Hadoop是一个由Apache基金会所开发的分…...

网站网页客服、微信公众号客服、H5客服、开源源码与高效部署的完美结合
随着互联网技术的飞速发展,企业与客户之间的沟通方式也在持续变革。在线客服系统作为一种新兴的沟通工具,已经成为提升企业服务质量、增强客户满意度的重要手段。本文将详细介绍在线客服系统的优势、功能以及如何高效部署,特别是推荐一款名为…...

1、Qt UI控件 -- qucsdk
前言:Qt编写的自定义控件插件的sdk集合,包括了各个操作系统的动态库文件以及控件的头文件和sdk使用demo。类似于Wpf中的LivChart2控件库,都是一些编译好的控件,可以直接集成到项目中。该控件是飞扬青云大神多年前开发的࿰…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...



