解密辛普森悖论：如何在数据分析中保持清醒头脑

解密辛普森悖论：如何在数据分析中保持清醒头脑

之前也参加fine Bi的 培训，学到了辛普森悖论，今天为大家介绍一下

---

---

前言

什么是辛普森悖论？来自维基百科是这么说的
辛普森悖论（英语：Simpson’s paradox），是概率和统计中的一种现象，其中趋势出现在几组数据中，但当这些组被合并后趋势消失或反转。 这个结果在社会科学和医学科学统计中经常遇到， 当频率数据被不恰当地给出因果解释时尤其成问题。当干扰变量和因果关系在统计建模中得到适当处理时，这个悖论就可以得到解决。 辛普森悖论已被用来说明统计误用可能产生的误导性结果[
该现象于20世纪初就有人讨论，但一直到1951年，爱德华·H·辛普森在他发表的论文中阐述此一现象后，该现象才算正式被描述解释。后来就以他的名字命名此悖论，即辛普森悖论。

我们来举一个例子

辛普森悖论的一个常见例子涉及职业棒球运动员的击球率。一名球员有可能在很多年里每年都比另一名球员有更高的击球率，但在如果把他们全部加起来反而低了，这些年里都有较低的击球率。当年份之间的击球数存在较大差异时，就会发生这种现象。数学家肯·罗斯 (Ken Ross)使用两位棒球运动员德里克·杰特 (Derek Jeter)和大卫·贾斯蒂斯 (David Justice ) 在 1995 年和 1996 年期间的击球率证明了这一点：

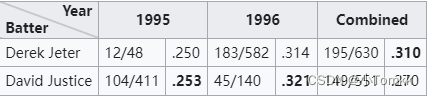
比如
A球员 1995 年 ，12/48 （48次击球，12次命中），击球率0.25，
B球员 1995 年 ，104/411 （411次击球，104次命中），击球率0.253
1995 年 击球率 是 B球员高

A球员 1996 年 ，183/582 （582次击球，183次命中），击球率0.314，
B球员 1996 年 ，45/140 （140次击球， 45次命中），击球率0.321，
1996 年 击球率 也是 B球员高

A球员 1995 年 和 1996 年 195/630 （630次击球，195次命中），击球率0.310
B球员 1995 年 和 1996 年 195/551 （551次击球，149次命中），击球率0.270
但是2年加起来 1995 年 和 1996 年 击球率 就是 A球员高

所以在做数据分析的时候 ，每年击球率都高，不代表 所有年份击球率都很高 所以 ，如果可能还需要下钻分析。

数据分析

为了避免辛普森悖论出现。就需要斟酌个别分组的权重，以一定的系数去消除以分组资料基数差异所造成的影响，同时必需了解该情境是否存在其他潜在要因而综合考虑

或者需要算 每年和汇总年份的都需要算出来，来斟酌数据分析。

解释

辛普森悖论是一个统计学术语
中文名：辛普森悖论
外文名：Simpson’s paradox
提出时间“”1951年
提出人：E.H.辛普森
理论学科：统计学
应用领域：数据分析

所以 辛普森悖论 这个词是一用来表示对于同一组数据，在分组中占尽优势而在总评中却处于劣势的悖论 ，出现这个悖论 的原因在于这些数据中存着“潜在变量”

---

管理应用的启示

来自科学百科的说明：

辛普森悖论就像是欲比赛100场篮球以总胜率评价好坏，于是有人专找高手挑战20 场而胜1场，另外80场找平手挑战而胜40场，结果胜率41%，另一人则专挑高手挑战80场而胜8场，而剩下20场平手打个全胜，结果胜率为28%，比 41%小很多，但仔细观察挑战对象，后者明显较有实力。
量与质是不等价的，无奈的是量比质来得容易量测，所以人们总是习惯用量来评定好坏，而此数据却不是重要的。除了质与量的迷思之外，辛普森悖论的另外一个启示是：如果我们在人生的抉择上选择了一条比较难走的路，就得要有可能不被赏识的领悟，所以这算是怀才不遇这个成语在统计上的诠释。

除了质与量的迷思之外，辛普森悖论的另外一个启示是： 如果我们在人生的抉择上选择了一条比较难走的路，就得要有可能不被赏识的领悟，所以这算是怀才不遇这个成语在统计学上的诠释。

---