当前位置： 首页 > news >正文

波士顿房价预测案例（python scikit-learn）---多元线性回归(多角度实验分析)

news 2025/8/29 0:24:41

波士顿房价预测案例（python scikit-learn）—多元线性回归(多角度实验分析)

这次实验，我们主要从以下几个方面介绍：

一、相关框架介绍

二、数据集介绍

三、实验结果-优化算法对比实验，数据标准化对比实验，正则化对比试验，多项式回归degree对比实验，岭回归alpha敏感度实验

一、相关框架介绍

Scikit-learn（全称：Simple and Efficient Tools for Machine Learning，意为“简单高效的机器学习工具”）是一个开源的Python机器学习库，它提供了简单而高效的工具，用于数据挖掘和数据分析。

Scikit-learn主要特点包括：丰富的算法库、易于使用、高效的性能、数据预处理和特征选择、模型评估和选择、可扩展性、社区支持。

二、数据集介绍

2.1数据集来源

波士顿房价数据集是一个著名的数据集，它在机器学习和统计分析领域中被广泛用于回归问题的实践和研究。这个数据集包含了美国马萨诸塞州波士顿郊区的房价信息，这些信息是由美国人口普查局收集的。
在这里插入图片描述
该数据集共包括507行数据，十三列特征，外加一列标签。

2.2数据集特征

数据集的特征：
CRIM: 城镇人均犯罪率 ZN: 占地面积超过25,000平方英尺的住宅用地比例
INDUS: 每个城镇非零售业务的比例 CHAS: 查尔斯河虚拟变量（如果是河道，则为1;否则为0）
NOX: 一氧化氮浓度（每千万份） RM: 每间住宅的平均房间数
AGE: 1940年以前建造的自住单位比例 DIS: 波士顿的五个就业中心加权距离
RAD: 径向高速公路的可达性指数 TAX: 每10,000美元的全额物业税率
PTRATIO: 城镇的学生与教师比例 B: 1000（Bk - 0.63）^ 2，其中Bk是城镇黑人的比例
LSTAT: 人口状况下降％ MEDV: 自有住房的中位数报价, 单位1000美元

三、实验结果-优化算法对比实验，数据标准化对比实验，正则化对比试验，多项式回归degree对比实验，岭回归alpha敏感度实验

3.1 优化算法对比实验


# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():lr = LinearRegression()# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。sgdr = SGDRegressor()# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)ridge = Ridge(alpha=10)# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)# Lassolasso = Lasso(alpha=0.01)# 使用训练数据进行参数估计。lasso.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lasso_y_predict = lasso.predict(X_test)return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression')plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor")#plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10")#plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01")plt.title("lr,sdgr+"+ss+"性能对比图")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)#plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)#plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()#coding=gbk;def plot_line(X,y,model,name):#--------------------------------------------------------------#z是我们生成的等差数列，用来画出线性模型的图形。z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
plot_line(X,y,lr,'LinearRegression+'+ss)
plot_line(X,y,sgdr,'SGDRegressor+'+ss)
#plot_line(X,y,lasso,'lasso'+ss)
#plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4])

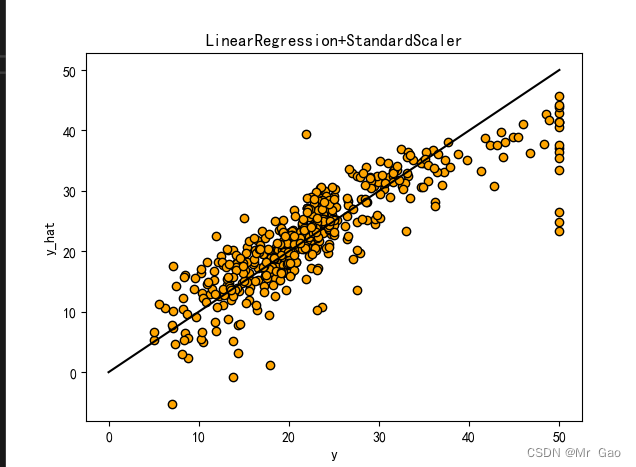
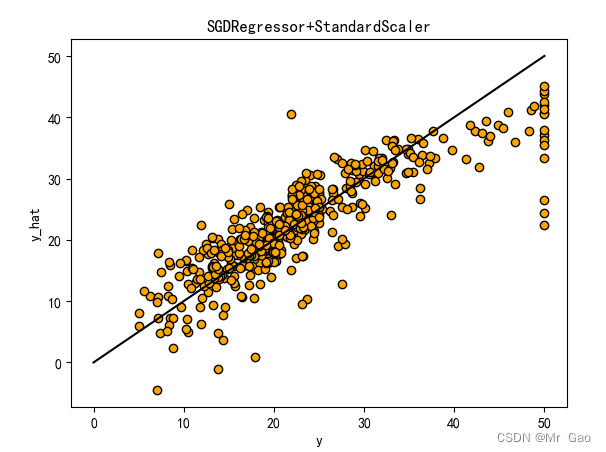
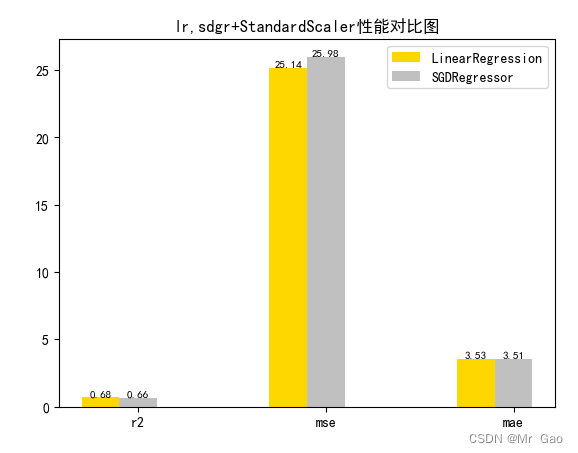
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.2 数据标准化对比实验

# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():lr = LinearRegression()# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。sgdr = SGDRegressor()# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)ridge = Ridge(alpha=10)# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)# Lassolasso = Lasso(alpha=0.01)# 使用训练数据进行参数估计。lasso.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lasso_y_predict = lasso.predict(X_test)return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression')plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor")#plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10")#plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01")plt.title("lr,sdgr+"+ss+"性能对比图")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)#plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)#plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()#coding=gbk;def plot_line(X,y,model,name):#--------------------------------------------------------------#z是我们生成的等差数列，用来画出线性模型的图形。z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
plot_line(X,y,lr,'LinearRegression+'+ss)
plot_line(X,y,sgdr,'SGDRegressor+'+ss)
#plot_line(X,y,lasso,'lasso'+ss)
#plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4])


# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge, RidgeCV
X = boston.data
print(X.min(axis=0))
print(X.max(axis=0))y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
# X_train = ss_X.fit_transform(X_train
# X_test = ss_X.transform(X_test)
y_train = y_train.reshape(-1, 1)
y_test = y_test.reshape(-1, 1)# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():lr = LinearRegression()# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。sgdr = SGDRegressor()# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)ridge = Ridge(alpha=10)# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)return lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(y_test, lr_y_predict)print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(y_test, lr_y_predict)print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression')plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor")# plt.bar(nmse_x,nmse,width=width, color="saddlebrown",label="mse")# plt.bar(mae_x,maes,width=width, color="red",label="mae")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)# plt.text(nmse_x[i],nmse[i], nmse[i],va="bottom",ha="center",fontsize=8)# plt.text(mae_x[i],maes[i], maes[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()def plot_line(X,y,model,name):#--------------------------------------------------------------#z是我们生成的等差数列，用来画出线性模型的图形。z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,model.predict(X),c="orange",edgecolors='k')print(model.predict(X))plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()
lr,sgdr,ridge,lr_y_predict,sgdr_y_predict,ridge_y_predict=train_model()models=[lr,sgdr,]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]plot_line(X,y,lr,'LinearRegression')
plot_line(X,y,sgdr,'SGDRegressor')
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)
plot(results[0][1:4],results[1][1:4])

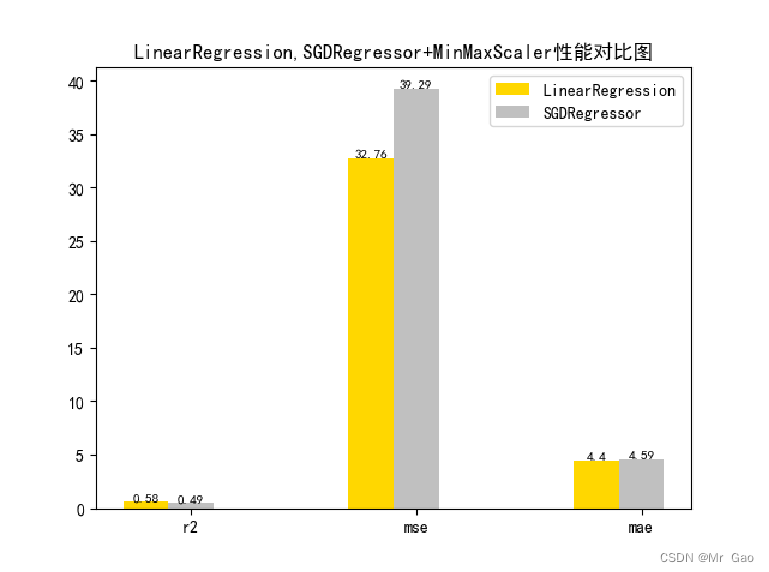
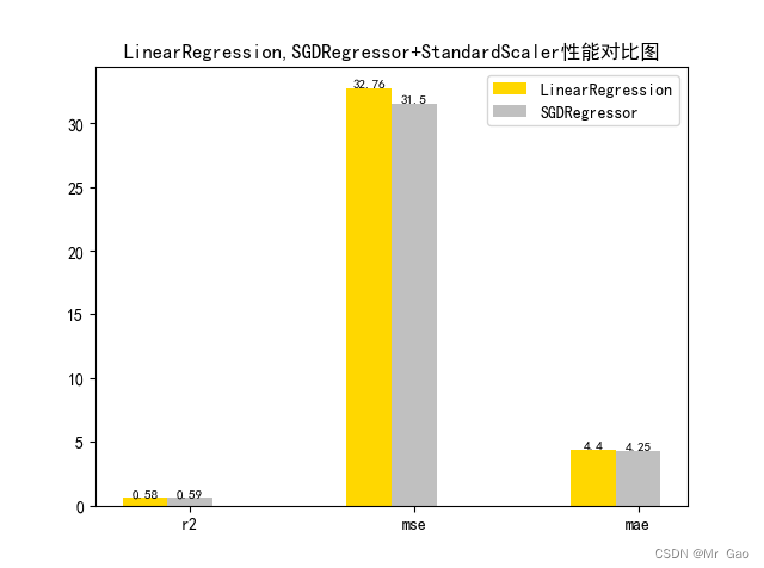
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.3 正则化对比试验


# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():lr = LinearRegression()# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。sgdr = SGDRegressor()# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)ridge = Ridge(alpha=10)# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)# Lassolasso = Lasso(alpha=0.01)# 使用训练数据进行参数估计。lasso.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lasso_y_predict = lasso.predict(X_test)return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2,model3,model4):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='LinearRegression')plt.bar(mess_x,model2,width=width,color="silver",label="SGDRegressor")plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10")plt.bar(mae_x,model4,width=width, color="red",label="lasso-alpha=0.01")plt.title("lr,sdgr,lasso,ridge+"+ss+"性能对比图")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()#coding=gbk;def plot_line(X,y,model,name):z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
plot_line(X,y,lr,'LinearRegression+'+ss)
plot_line(X,y,sgdr,'SGDRegressor'+ss)
plot_line(X,y,lasso,'lasso'+ss)
plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

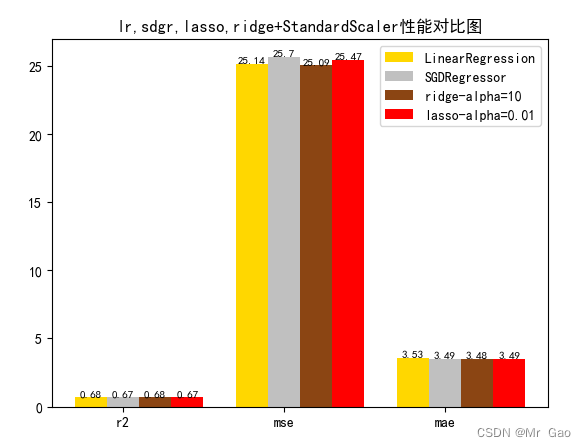
在这里插入图片描述

3.4多项式回归degree对比实验


# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train[0]=y_train[0]+300
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():poly_reg = PolynomialFeatures(degree=1)# 数据转换 x0-->1  x1-->x  x2-->x^2  x3-->x^3x_poly = poly_reg.fit_transform(X_train)# 建模#lin_reg = LinearRegression().fit(x_poly, y_data)lr = LinearRegression().fit(x_poly, y_train[:,0])# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。poly_reg = PolynomialFeatures(degree=2)# 数据转换 x0-->1  x1-->x  x2-->x^2  x3-->x^3x_poly = poly_reg.fit_transform(X_train)sgdr =  LinearRegression().fit(x_poly, y_train[:,0])# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)poly_reg = PolynomialFeatures(degree=3)# 数据转换 x0-->1  x1-->x  x2-->x^2  x3-->x^3x_poly = poly_reg.fit_transform(X_train)ridge =  LinearRegression().fit(x_poly, y_train[:,0])# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)# Lassopoly_reg = PolynomialFeatures(degree=4)# 数据转换 x0-->1  x1-->x  x2-->x^2  x3-->x^3x_poly = poly_reg.fit_transform(X_train)lasso = LinearRegression().fit(x_poly, y_train[:,0])# 使用训练数据进行参数估计。lasso.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lasso_y_predict = lasso.predict(X_test)return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2,model3,model4):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='ploy-degree=1')plt.bar(mess_x,model2,width=width,color="silver",label="ploy-degree=2")plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ploy-degree=3")plt.bar(mae_x,model4,width=width, color="red",label="ploy-degree=4")plt.title("不同degree多项式回归+"+ss+"性能对比图")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()#coding=gbk;def plot_line(X,y,model,name):#--------------------------------------------------------------#z是我们生成的等差数列，用来画出线性模型的图形。z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
#plot_line(X,y,lr,'LinearRegression+'+ss)
#plot_line(X,y,sgdr,'SGDRegressor'+ss)
#plot_line(X,y,lasso,'lasso'+ss)
#plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

截图：
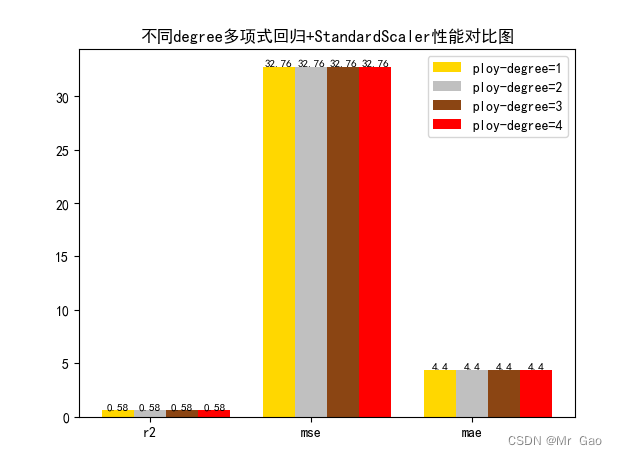
在这里插入图片描述

3.5 岭回归alpha敏感度实验


# 从 sklearn.datasets 导入波士顿房价数据读取器。
from sklearn.datasets import load_boston
# 从读取房价数据存储在变量 boston 中。
boston = load_boston()
# 输出数据描述。
from matplotlib import pyplot as plt
from matplotlib import font_manager
from matplotlib import pyplot as plt
import numpy as np
import matplotlib
# 参数设置import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题# 从sklearn.cross_validation 导入数据分割器。
from sklearn.model_selection import train_test_split
# 导入 numpy 并重命名为 np。
import numpy as np
from sklearn.linear_model import Ridge,Lasso
X = boston.data
y = boston.target
# 随机采样 25% 的数据构建测试样本，其余作为训练样本。X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)
# 分析回归目标值的差异。print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target)) 
print("The average target value is", np.mean(boston.target))# 从 sklearn.preprocessing 导入数据标准化模块。
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
# 分别初始化对特征和目标值的标准化器。
ss_X = StandardScaler()
ss_y = StandardScaler()
ss="StandardScaler"
# 分别对训练和测试数据的特征以及目标值进行标准化处理。
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train[0]=y_train[0]+300
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))y_test = ss_y.transform(y_test.reshape(-1, 1))# 从 sklearn.linear_model 导入 LinearRegression。
from sklearn.linear_model import LinearRegression
# 使用默认配置初始化线性回归器 LinearRegression。def train_model():lr = Ridge(alpha=2)# 使用训练数据进行参数估计。lr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lr_y_predict = lr.predict(X_test)# 从 sklearn.linear_model 导入 SGDRegressor。from sklearn.linear_model import SGDRegressor# 使用默认配置初始化线性回归器 SGDRegressor。sgdr = Ridge(alpha=5)# 使用训练数据进行参数估计。sgdr.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。sgdr_y_predict = sgdr.predict(X_test)ridge = Ridge(alpha=10)# 使用训练数据进行参数估计。ridge.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。ridge_y_predict = ridge.predict(X_test)# Lassolasso =Ridge(alpha=15)# 使用训练数据进行参数估计。lasso.fit(X_train, y_train[:,0])# 对测试数据进行回归预测。lasso_y_predict = lasso.predict(X_test)return lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predictdef evaluate(X_test,y_test,lr_y_predict,model):
# 使用 LinearRegression 模型自带的评估模块，并输出评估结果。nmse=model.score(X_test, y_test)print('The value of default measurement of LinearRegression is',nmse )# 从 sklearn.metrics 依次导入 r2_score、mean_squared_error 以及 mean_absoluate_error 用于回归性能的评估。from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# 使用 r2_score 模块，并输出评估结果。r2=r2_score(y_test, lr_y_predict)print('The value of R-squared of LinearRegression is',r2 )# 使用 mean_squared_error 模块，并输出评估结果。#print(y_test)lr_y_predict=lr_y_predict.reshape(len(lr_y_predict),-1)#print(lr_y_predict)#print(mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))mse=mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean squared error of LinearRegression is',mse)# 使用 mean_absolute_error 模块，并输出评估结果。mae= mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))print('The mean absoluate error of LinearRegression is', mae)return round(nmse,2),round(r2,2),round(mse,2),round(mae,2)def plot(model1,model2,model3,model4):
# 数据classes = [ 'r2', 'mse', 'mae']# r2s = [87, 85, 89, 81, 78]# mess = [85, 98, 84, 79, 82]# nmse = [83, 85, 82, 87, 78]# 将横坐标班级先替换为数值x = np.arange(len(classes))width = 0.2r2s_x = xmess_x = x + widthnmse_x = x + 2 * widthmae_x = x + 3 * width# 绘图plt.bar(r2s_x, model1, width=width, color='gold', label='ridge-alpha=2')plt.bar(mess_x,model2,width=width,color="silver",label="ridge-alpha=5")plt.bar(nmse_x,model3,width=width, color="saddlebrown",label="ridge-alpha=10")plt.bar(mae_x,model4,width=width, color="red",label="ridge-alpha=15")plt.title("不同alpha-ridge+"+ss+"性能对比图")#将横坐标数值转换为班级plt.xticks(x + width, classes)#显示柱状图的高度文本for i in range(len(classes)):plt.text(r2s_x[i],model1[i], model1[i],va="bottom",ha="center",fontsize=8)plt.text(mess_x[i],model2[i], model2[i],va="bottom",ha="center",fontsize=8)plt.text(nmse_x[i],model3[i], model3[i],va="bottom",ha="center",fontsize=8)plt.text(mae_x[i],model4[i], model4[i],va="bottom",ha="center",fontsize=8)#显示图例plt.legend(loc="upper right")plt.show()#coding=gbk;def plot_line(X,y,model,name):#--------------------------------------------------------------#z是我们生成的等差数列，用来画出线性模型的图形。z=np.linspace(0,50,200).reshape(-1,1)plt.scatter(y,ss_y.inverse_transform(model.predict(ss_X.transform(X)).reshape(len(X),-1)),c="orange",edgecolors='k')plt.plot(z,z,c="k")plt.xlabel('y')plt.ylabel("y_hat")plt.title(name)plt.show()lr,sgdr,ridge,lasso,lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict=train_model()models=[lr,sgdr,ridge,lasso]
r2s=[]
mess=[]
maes=[]
nmse=[]
results=[]
plot_line(X,y,lr,'LinearRegression+'+ss)
plot_line(X,y,sgdr,'SGDRegressor'+ss)
plot_line(X,y,lasso,'lasso'+ss)
plot_line(X,y,ridge,'ridge'+ss)
print("sgdr_y_predict")
print(sgdr_y_predict)predicts=[lr_y_predict,sgdr_y_predict,ridge_y_predict,lasso_y_predict]
i=0
for model in models:result=evaluate(X_test,y_test,predicts[i],model)i=i+1results.append(result)# r2s.append(result[1])# mess.append(result[2])# maes.append(result[3])# nmse.append(result[0])#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
print(results)#evaluate(X_test,y_test,sgdr_y_predict,sgdr)
plot(results[0][1:4],results[1][1:4],results[2][1:4],results[3][1:4])

运行结果：
在这里插入图片描述

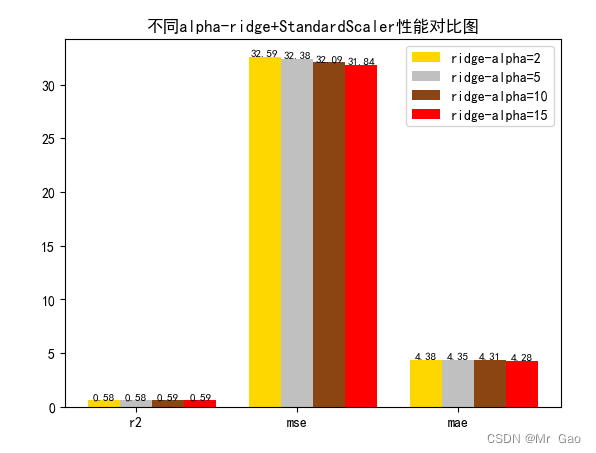
相关文章：

波士顿房价预测案例（python scikit-learn）---多元线性回归(多角度实验分析)

波士顿房价预测案例（python scikit-learn）—多元线性回归(多角度实验分析) 这次实验，我们主要从以下几个方面介绍： 一、相关框架介绍 二、数据集介绍 三、实验结果-优化算法对比实验，数据标准化对比实验&#xff0…...

编程日记 2024/4/12 2:18:06

在 Queue 中 poll()和 remove()有什么区别？

在Java的Queue接口中，poll()和remove()方法都用于从队列中删除并返回队列的头部元素，但是它们在队列为空时的行为有所不同。 poll()方法：当队列为空时，poll()方法会返回null，而不会抛出异常。这是它的主要特点&#x…...

编程日记 2024/4/12 2:06:55

实现鼠标在页面点击出现焦点及大十字星

近段时间，在完成项目进度情况显示时候，用户在操作鼠标时候，显示当鼠标所在位置对应时间如下图所示 代码实现步骤如下： 1.首先引用 jquery.1.7.js 2.再次引用raphael.js 3.然后引用graphics.js 4.最后引用mfocus.js 其中mfocu…...

编程日记 2024/4/12 2:03:52

如何在 7 天内掌握C++？

大家好，我是小康，今天我们来聊下如何快速学习 C 语言。 本篇文章适合于有 C 语言编程基础的小伙伴们，如果还没有学习过 C，请看这篇文章先入个门：C语言快速入门 引言： C，作为一门集面向过程和…...

编程日记 2024/4/12 2:02:50

FineBI概述

FineBI是一种商业智能（BI）软件，旨在帮助企业从数据中获取见解并做出更明智的业务决策。以下是FineBI的详细概述： 功能特性： 数据连接与整合：FineBI可以连接到各种数据源，包括数据库、数据仓库、…...

编程日记 2024/4/12 1:58:45

百度Create AI开发者大会剧透丨用好三大AI神器 ，人人都是开发者

程序员会消失，真的吗？大模型的下一站是什么？开发者的机会在哪里？什么才是最好用的AI应用开发工具？在4月16日举办的2024百度Create AI开发者大会上，百度创始人、董事长兼首席执行官李彦宏将就这些备受瞩目的…...

编程日记 2024/4/12 1:57:43

外包干了17天，技术倒退明显

先说情况，大专毕业，18年通过校招进入湖南某软件公司，干了接近6年的功能测试，今年年初，感觉自己不能够在这样下去了，长时间呆在一个舒适的环境会让一个人堕落！ 而我已经在一个企业干了四年的功能…...

编程日记 2024/4/12 1:56:42

Unity类银河恶魔城学习记录12-8 p130 Skill Tree UI源代码

Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释，可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili UI.cs using UnityEngine;public class UI : MonoBehaviour {[SerializeFi…...

编程日记 2024/4/12 1:53:40

priority_queue的使用以及模拟实现

前言 上一期我们对stack和queue进行了使用的介绍，以及对底层的模拟实现！以及容器适配器做了介绍，本期我们在来介绍一个容器适配器priority_queue！ 本期内容介绍 priority_queue的使用 仿函数介绍 priority_queue的模拟实现 什么…...

编程日记 2024/4/12 1:52:38

主机有被植入挖矿病毒篡改系统库文件

查看主机有被植入挖矿病毒篡改系统库文件的行为 排查方法 挖矿病毒被植入主机后，利用主机的运算力进行挖矿，主要体现在CPU使用率高达90%以上，有大量对外进行网络连接的日志记录。 Linux主机中挖矿病毒后的现象如下图所示： &…...

编程日记 2024/4/12 1:51:37

Python 推导式介绍

Python推导式是一种简洁而强大的语法，用于在一行代码中创建集合（list、set、dictionary）的方式。推导式使得代码更加简洁易读，提高了代码的可读性和可维护性。Python中有列表推导式、集合推导式和字典推导式三种类型。 列表推导式…...

编程日记 2024/4/12 1:49:36

VUE3和SpringBoot实现ChatGPT页面打字效果SSE流式数据展示

在做这个功能之前，本人也是走了很多弯路（花了好几天才搞好），你能看到本篇博文，那你就是找对地方了。百度上很多都是使用SseEmitter这种方式，这种方式使用的是websocket，使用这种方式就搞复杂了&…...

编程日记 2024/4/12 1:48:34

ClickHouse入门篇:一文带你学习ClickHouse

ClickHouse 是一个用于联机分析处理(OLAP)的列式数据库管理系统(DBMS)。由于其独特的数据存储和处理架构，ClickHouse 能够提供高速数据插入和实时查询性能。下面是对 ClickHouse 的详细介绍，包括其特性、应用场景和架构： 特性 列式存储: 数…...

编程日记 2024/4/12 1:47:33

基于小程序实现的校园失物招领系统

作者主页：Java码库 主营内容：SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】：Java 【框架】：spring…...

编程日记 2024/4/12 1:46:29

损失函数篇 | YOLOv8更换损失函数之Powerful-IoU（2024年最新IoU）

前言：Hello大家好，我是小哥谈。损失函数是机器学习中用来衡量模型预测值与真实值之间差异的函数。在训练模型时，我们希望通过不断调整模型参数，使得损失函数的值最小化，从而使得模型的预测值更加接近真实值。不同的损失函数适用于不同的问题，例如均方误差损失函数适用于回…...

编程日记 2024/4/12 1:45:28

（学习日记）2024.04.11：UCOSIII第三十九节：软件定时器

写在前面： 由于时间的不足与学习的碎片化，写博客变得有些奢侈。 但是对于记录学习（忘了以后能快速复习）的渴望一天天变得强烈。 既然如此 不如以天为单位，以时间为顺序，仅仅将博客当做一个知识学习的目录&a…...

编程日记 2024/4/12 1:44:27

wordpress全站开发指南-面向开发者及深度用户（全中文实操）--wordpress是什么

WordPress简介 WordPress是一个开源的内容管理系统（CMS），广泛用于创建和管理网站。它最初是作为一个博客平台开始的，但现在已经发展成为一个功能强大的网站建设工具，可以用于创建各种类型的网站，包括个人博…...

编程日记 2024/4/12 1:43:26

瑞_23种设计模式_访问者模式

文章目录 1 访问者模式（Visitor Pattern）1.1 介绍1.2 概述1.3 访问者模式的结构1.4 访问者模式的优缺点1.5 访问者模式的使用场景 2 案例一2.1 需求2.2 代码实现 3 案例二3.1 需求3.2 代码实现 4 拓展——双分派4.1 分派4.2 动态分派（多态&am…...

编程日记 2024/4/12 1:42:25

Docker网络代理配置 可能埋下的坑

Docker 网络代理配置 1. 在 /etc/systemd/system 目录下创建 docker.service.d 目录 sudo mkdir -p /etc/systemd/system/docker.service.d2. 在/etc/systemd/system/docker.service.d下创建 http-proxy.conf 文件 sudo touch /etc/systemd/system/docker.service.d/http-pr…...

编程日记 2024/4/12 1:41:21

外包干了3天，技术退步明显.......

先说一下自己的情况，大专生，19年通过校招进入杭州某软件公司，干了接近4年的功能测试，今年年初，感觉自己不能够在这样下去了，长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...

编程日记 2024/4/12 1:40:20

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2025/8/28 15:32:59

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动

一、前言说明 在2011版本的gb28181协议中，拉取视频流只要求udp方式，从2016开始要求新增支持tcp被动和tcp主动两种方式，udp理论上会丢包的，所以实际使用过程可能会出现画面花屏的情况，而tcp肯定不丢包，起码…...

编程新知 2025/8/24 20:40:24

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2025/8/22 7:03:09

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2025/7/23 10:55:13

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2025/8/26 18:03:38

云原生玩法三问：构建自定义开发环境

云原生玩法三问&#xff1a;构建自定义开发环境 引言 临时运维一个古董项目&#xff0c;无文档&#xff0c;无环境&#xff0c;无交接人&#xff0c;俗称三无。 运行设备的环境老&#xff0c;本地环境版本高&#xff0c;ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

编程新知 2025/8/24 18:20:32

Python竞赛环境搭建全攻略

Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型&#xff08;算法、数据分析、机器学习等&#xff09;不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

编程新知 2025/7/8 4:17:48

API网关Kong的鉴权与限流：高并发场景下的核心实践

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中&#xff0c;API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关&#xff0c;Kong凭借其插件化架构…...

编程新知 2025/7/9 6:59:52

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能

指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

编程新知 2025/8/11 18:29:12