《一》Qt的概述
1.1 什么是Qt
Qt是一个跨平台的C++图形用户界面应用程序框架。它为应用程序开发者提供建立图形界面所需的所有功能。它是完全面向对象的，很容易扩展，并且允许真正的组件编程。
1.2 Qt的发展史
1991年 Qt最早由芬兰奇趣科技开发
1996年 进入商业领域，它也是目前流行的Linux桌面环境KDE的基础
2008年 奇趣科技被诺基亚公司收购，Qt称为诺基亚旗下的编程基础
2012年 Qt又被Digia公司（芬兰一家软件公司）收购
2014年4月 跨平台的集成开发环境Qt Creator3.1.0发布，同年5月20日配发了Qt5.3正式版，至此Qt实现了对iOS、Android、WP等各平台的全面支持。
1.3 Qt的优势
1)跨平台，几乎支持所有的平台
2)接口简单，容易上手，学习QT框架对学习其他框架有参考意义。
3)一定程度上简化了内存回收机制
4)开发效率高，能够快速的构建应用程序。
5)有很好的社区氛围，市场份额在缓慢上升。
6)可以进行嵌入式开发。
1.4 Qt版本
Qt按照不同的版本发行，分为商业版和开源版
商业版
为商业软件提供开发，他们提供传统商业软件发行版，并且提供在商业有效期内的免费升级和技术支持服务。
开源的LGPL协议版本：
为了开发自有而设计的开放源码软件，它提供了和商业版本同样的功能，在GNU通用公共许可下，它是免费的。
目前我们学习上使用的就是这个版本。可以到官网下载最新版本：Index of /archive/qt
https://download.qt.io/archive/qt/
具体的环境搭建：
环境搭建 · 恋恋风辰的编程笔记
感谢观看！！！！！
相关文章：
《一》Qt的概述
1.1 什么是Qt Qt是一个跨平台的C图形用户界面应用程序框架。它为应用程序开发者提供建立图形界面所需的所有功能。它是完全面向对象的，很容易扩展，并且允许真正的组件编程。 1.2 Qt的发展史 1991年 Qt最早由芬兰奇趣科技开发 1996年 进入商业领域&#x…...
局域网共享文件夹怎么加密？局域网共享文件夹加密方法介绍
在企业局域网中，共享文件夹扮演着重要的角色。为了保护数据安全，我们需要加密保护局域网共享文件夹。那么，局域网共享文件夹怎么加密？下面我们来了解一下吧。 局域网共享文件夹加密方法 局域网共享文件夹加密推荐使用共享文件夹加…...
计算机网络——网络地址转换（NAT）技术
目录 前言 前篇 引言 SNAT（Source Network Address Translation）源网络地址转换 SNAT流程 确定性标记 DNAT（Destination Network Address Translation，目标网络地址转换） NAT技术重要性 前言 本博客是博主用于…...
【感谢】心怀感恩，共赴知识之旅——致每一位陪伴我突破百万总访问量的您
小伙伴朋友们： 此刻，我怀着无比激动与深深感激的心情，写下这篇特别的博文。今天，我的CSDN总访问量成功突破了百万大关，这不仅是一个数字的跨越，更是你们对我的支持、信任与鼓励的有力见证。在此࿰…...
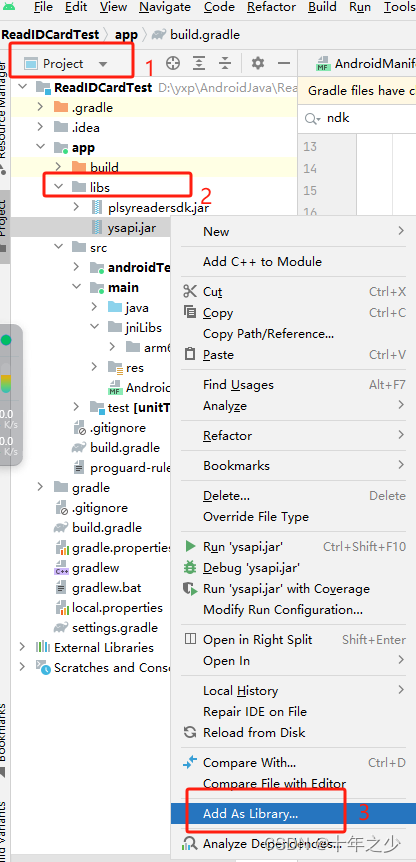
Android Studio导入第三方so库和jar包——Android Studio
导入so库 方式一（libs文件夹） 将项目以【Project】的结构显示，将目标架构对应的so文件夹（如下图中 的arm64-v8a）复制粘贴到app文件下的lib文件夹中（如下图的步骤1 2 3） 在build.gradle&…...
jeecg-boot 3.6使用微服务启动详细配置
1：运行sql文件 2：配置host 路径如下 127.0.0.1 jeecg-boot-redis 127.0.0.1 jeecg-boot-mysql 127.0.0.1 jeecg-boot-nacos 127.0.0.1 jeecg-boot-gateway 127.0.0.1 jeecg-boot-system 127.0.0.1 jeecg-boot-xxljob 127.0.0.1 jeecg-boot-rabbitmq 3…...
【Android】【root remount】【2】如何判断设备是否remount
前言 高版本的android设备，在remount之后，如果再进行ota升级，会产生异常，从而无法升级成功。 如何判断设备是否remount 当前已android 10 平台为例 当我们执行 adb remount 时，系统调用会调用到system/core/adb/dae…...
html中的“居中”问题详解（超全）
html中的“居中”问题详解（超全） 图片居中文本居中定位居中元素居中响应式设计中的居中技巧 引言： 在网页设计和开发中，实现元素的居中是一个常见但也常被低估的挑战。无论是在传统的网页布局中还是在响应式设计中，居中…...
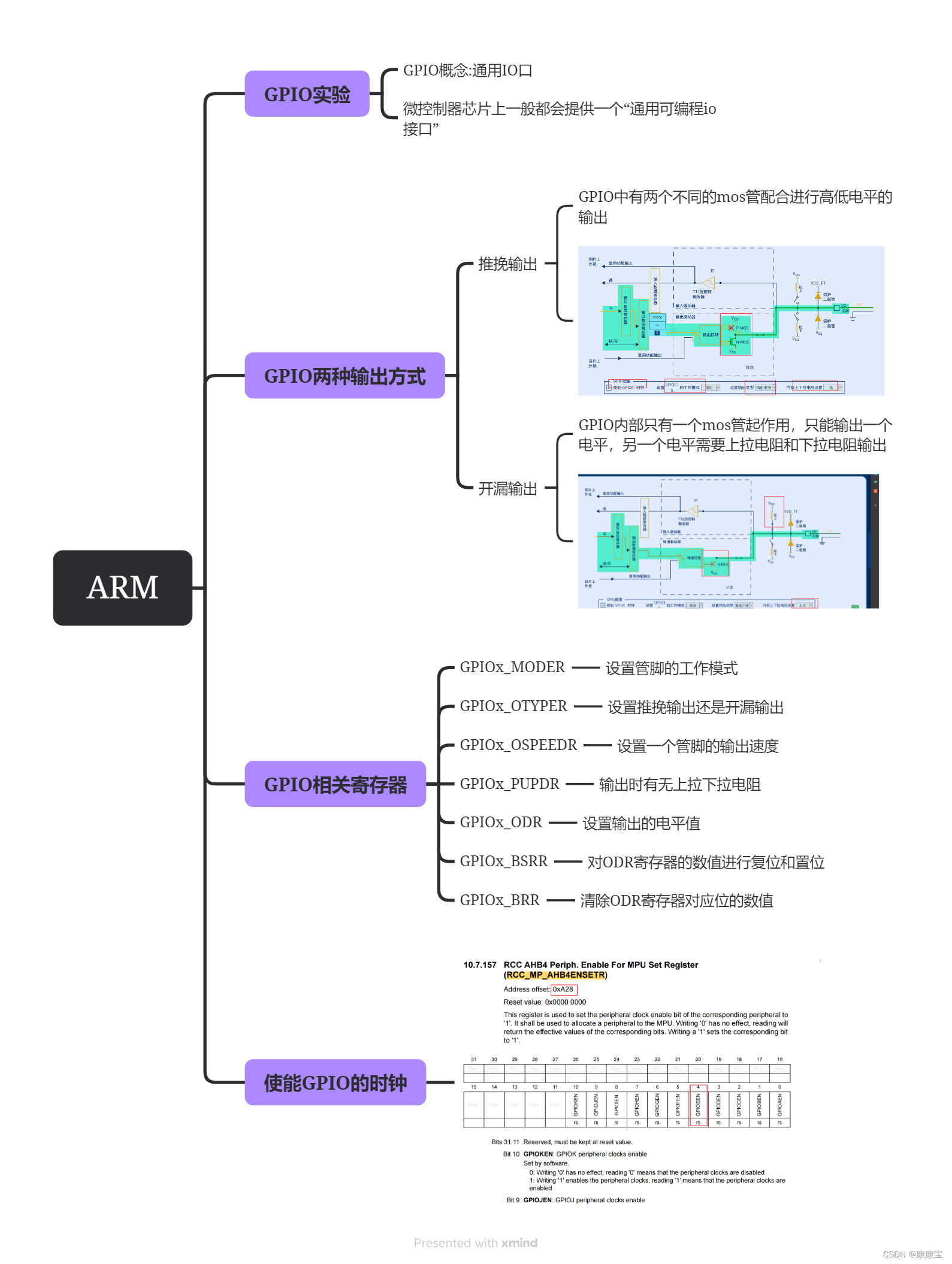
【嵌入式学习】ARM day04.11
一、思维导图 二、练习 实现三个灯闪烁 汇编代码 .text .global _start _start: 使能GPIOE和F时钟LDR r0,0x50000A28LDR r1,[R0]ORR R1,R1,#(0X3<<4)STR R1,[R0]配置GPIOE和F的MODER寄存器LDR r0,0x50006000 GPIOELDR R1,0X50007000 G…...
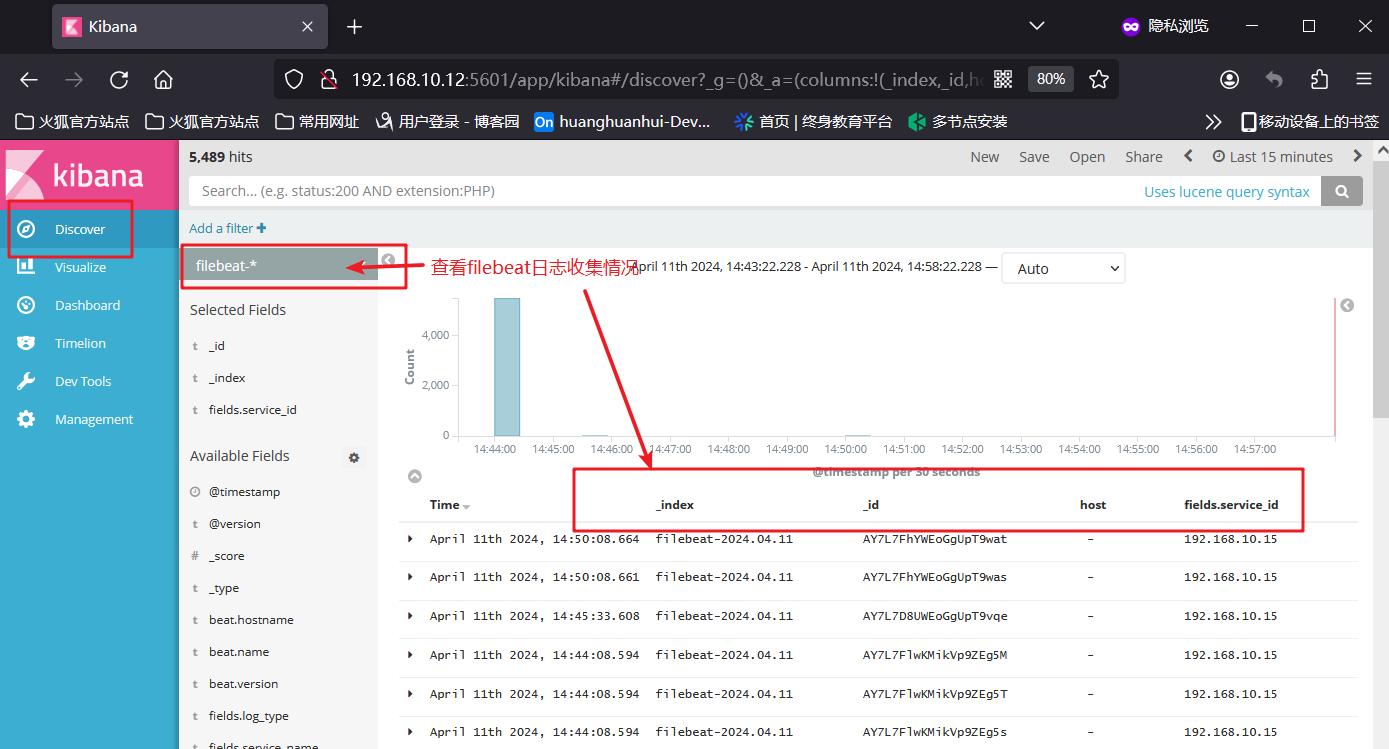
关于部署ELK和EFLKD的相关知识
文章目录 一、ELK日志分析系统1、ELK简介1.2 ElasticSearch1.3 Logstash1.4 Kibana（展示数据可视化界面）1.5 Filebeat 2、使用ELK的原因3、完整日志系统的基本特征4、ELK的工作原理 二、部署ELK日志分析系统1、服务器配置2、关闭防火墙3、ELK ElasticSea…...
ChatGPT智能写作：开启论文写作新视野
ChatGPT无限次数:点击直达 html ChatGPT智能写作：开启论文写作新视野 引言 在当今信息爆炸的时代，人们需要更有效的工具来帮助他们在各种领域进行写作。ChatGPT作为一项基于人工智能技术的顶尖产品，为论文写作提供了全新的视角和可能性。…...
网络安全---RSA公钥加密与签名
实验项目：RSA公钥加密与签名实验 1.实验目的 本实验的学习目标是让学生获得 RSA 算法的动手经验。 通过课堂学习，学生应该已经了解 RSA 算法的理论部分， 知道在数学上如何生成公钥、私钥以及如何执行加密、解密和签名生成、验证。 通过使用…...
李白打酒加强版 -- 题解 c++
题目链接 : 4408. 李白打酒加强版 - AcWing题库 用户登录 二进制搜索 只能过10%,极限暴力 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \n typedef long long LL; const int mod 1e97; const int N 2e510;…...
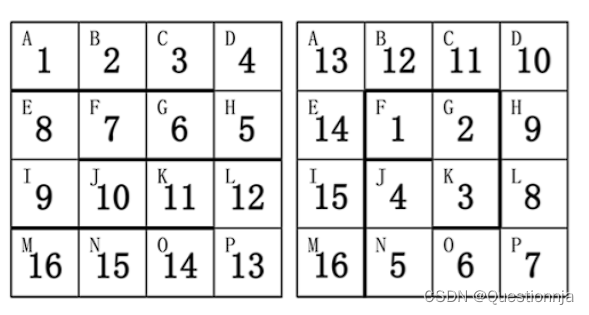
蓝桥杯——玩具蛇
题目 小蓝有—条玩具蛇，一共有16节，上面标着数字1至16。每—节都是一个正方形的形状。相邻的两节可以成直线或者成90度角。 小蓝还有一个44的方格盒子，用于存放玩具蛇，盒子的方格上依次标着字母A到Р共16个字母。 小蓝可以折叠自…...
百度SSL证书免费申请
百度云也有免费SSL证书可以申请，很多用户找不到，云服务器吧yunfuwuqiba.com整理百度云SSL免费证书申请入口： 1、打开百度云SSL证书购买页面 yunfuwuqiba.com/go/baidu_ssl 点立即购买，如下图： 百度云SSL证书 2、免费…...
SpringBoot Assert断言
文章目录 前言一、Assert说明二、Assert方法三、使用示例四、总结前言 在Spring Boot中，Assert类提供了一系列用于断言的静态方法，用于在代码中进行条件检查和错误处理。这些方法可以帮助我们在开发过程中快速发现和解决问题，提高代码的可靠性和健壮性。 一、Assert说明 在…...
test4121
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起学习和分享Linux、C、C、Python、Matlab，机器人运动控制、多机器人协作，智能优化算法，滤波估计、多传感器信息融合，机器学习，人工智能等相关领域的知识和…...
UI自动化测试重点思考(下)--装饰器/生成器/夹具的使用/描述符的作用/ddt驱动/多线程
UI自动化测试重点思考--装饰器 装饰器装饰器定义装饰器代码示例装饰器的执行如何将装饰器融合到pytest框架里面 生成器创建生成器生成器的定义如何将生成器融合到pytest框架里面 fixture（夹具）使用pytest fixture 中 scope 参数的详细解释 描述符的总结描…...
C# 字段和属性的区别
区别 在C#中，字段（Field）和属性（Property）都是用来封装对象状态的方式，但它们有以下区别： 访问级别： 字段通常是private，而属性可以有不同级别的访问限制（…...
备考ICA----Istio实验17---TCP流量授权
备考ICA----Istio实验17—TCP流量授权 1. 环境准备 1.1 环境部署 kubectl apply -f <(istioctl kube-inject -f istio/samples/tcp-echo/tcp-echo.yaml) -n kim kubectl apply -f <(istioctl kube-inject -f istio/samples/sleep/sleep.yaml) -n kim1.2 测试环境 检测…...
IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周，有很多同学在写期末Java web作业时，运行tomcat出现乱码问题，经过多次解决与研究，我做了如下整理： 原因： IDEA本身编码与tomcat的编码与Windows编码不同导致，Windows 系统控制台…...
(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目：3442. 奇偶频次间的最大差值 I 思路 ：哈希，时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况，哈希表这里用数组即可实现。 C版本： class Solution { public:int maxDifference(string s) {int a[26]…...
STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
pam_env.so模块配置解析
在PAM（Pluggable Authentication Modules）配置中， /etc/pam.d/su 文件相关配置含义如下： 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块，负责验证用户身份&am…...
使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui（适配 Vue2 版本 ）实现截图中照片上传预览、删除功能，并封装成可复用组件的完整代码，包含样式和逻辑实现，可直接在 Vue2 项目中使用： 1. 封装的图片上传组件 ImageUploader.vue <te…...
在Ubuntu中设置开机自动运行（sudo）指令的指南
在Ubuntu系统中，有时需要在系统启动时自动执行某些命令，特别是需要 sudo权限的指令。为了实现这一功能，可以使用多种方法，包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法，并提供…...
【C++进阶篇】智能指针
C内存管理终极指南：智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机，它可以执行Java字节码。Java虚拟机是Java平台的一部分，Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
【Kafka】Kafka从入门到实战：构建高吞吐量分布式消息系统
Kafka从入门到实战：构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台，最初由LinkedIn开发，后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理，能够处理来自多个生产者的海量数据，并将这些数据实时传递给消费者。 Kafka核心特…...