备战蓝桥杯---刷杂题2
显然我们直接看前一半,然后我们按照斜行看,我们发现斜行是递增的,而同一行从左向右也是递增的,因此我们可以直接二分,同时我们发现对称轴的数为Ck,2k.
我们从16斜行枚举即可
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
LL C(int a,int b){LL res=1;for(int i=a,j=1;j<=b;i--,j++){res=res*i/j;if(res>n) return res;}return res;
}
bool check(int k){LL l=k*2,r=n;if(l>r) return 0;while(l<r){LL mid=l+r>>1;if(C(mid,k)>=n) r=mid;else l=mid+1;}if(C(r,k)!=n) return 0;cout<<(r+1)*r/2+k+1;return 1;
}
int main(){cin>>n;for(int k=16;;k--){if(check(k)){break;}}
}2.spfa的本质(妙)

我们令f[i][j]表示在i步以内可以生成j作物的方法的集合,我们记录其最小时间,答案就是f[n-1][t],对于初始值,f[0][xi]=0,对于f[i][j],我们可以看看j的生成方式即可,即f[i][j]=min(f[i][j],max(f[i-1][x],f[i-1][y])),复杂度为(n-1)k,我们加个spfa思想优化,j是由x,y更新的,只有x,y更新j才可能更新,
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2010,M=200010;
int n,m;
int h[N],e[M],w[N],target[M],ne[M],idx;
int dis[N];
queue<int> q;
bool st[N];
void add(int a,int b,int c){e[idx]=b,target[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa(){while(q.size()){int x=q.front();q.pop();st[x]=0;for(int i=h[x];i!=-1;i=ne[i]){int y=e[i],z=target[i];if(dis[z]>max(dis[x],dis[y])+max(w[x],w[y])){dis[z]=max(dis[x],dis[y])+max(w[x],w[y]);if(!st[z]){q.push(z);st[z]=1;}}}}
}
int main(){int k,T;cin>>n>>m>>k>>T;memset(h,-1,sizeof(h));for(int i=1;i<=n;i++) scanf("%d",&w[i]);memset(dis,0x3f,sizeof(dis));while(m--){int x;scanf("%d",&x);dis[x]=0;q.push(x);st[x]=1;}while(k--){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);add(b,a,c);}spfa();cout<<dis[T];
}3.欧拉函数:

下面是数学推导:
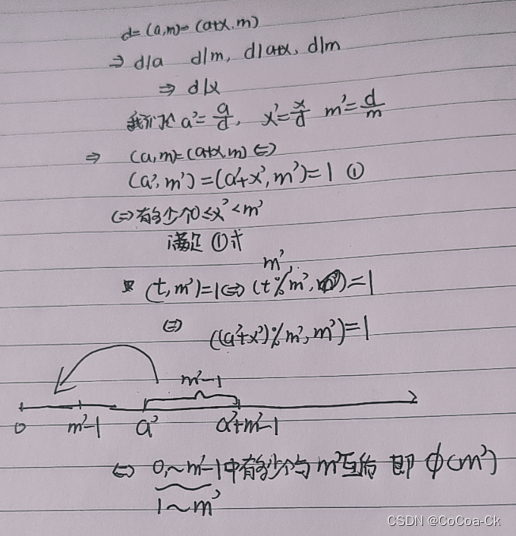
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){return b?gcd(b,a%b):a;
}
LL phi(LL m){LL res=m;for(LL i=2;i<=m/i;i++){if(m%i==0){while(m%i==0) m/=i;res=res/i*(i-1);}}if(m>1) res=res/m*(m-1);return res;
}
int main(){int T;cin>>T;while(T--){LL a,m;cin>>a>>m;LL d=gcd(a,m);cout<<phi(m/d)<<endl;}
}相关文章:
备战蓝桥杯---刷杂题2
显然我们直接看前一半,然后我们按照斜行看,我们发现斜行是递增的,而同一行从左向右也是递增的,因此我们可以直接二分,同时我们发现对称轴的数为Ck,2k. 我们从16斜行枚举即可 #include<bits/stdc.h> using name…...
.[[backup@waifu.club]].svh勒索病毒数据怎么处理|数据解密恢复
尊敬的读者: 近年来,随着信息技术的迅猛发展,网络安全问题日益凸显,其中勒索病毒成为了一大威胁。.[[backupwaifu.club]].svh、.[[MyFilewaifu.club]].svh勒索病毒就是其中之一,它以其独特的传播方式和恶劣的加密手段…...
)
SpringFramework实战指南(八)
SpringFramework实战指南(八) 5.1 场景设定和问题复现5.2 解决技术代理模式5.1 场景设定和问题复现 准备AOP项目 项目名:spring-aop-annotation pom.xml <dependencies><!--spring context依赖--><!--当你引入Spring Context依赖之后,表示将Spring的基础依赖…...
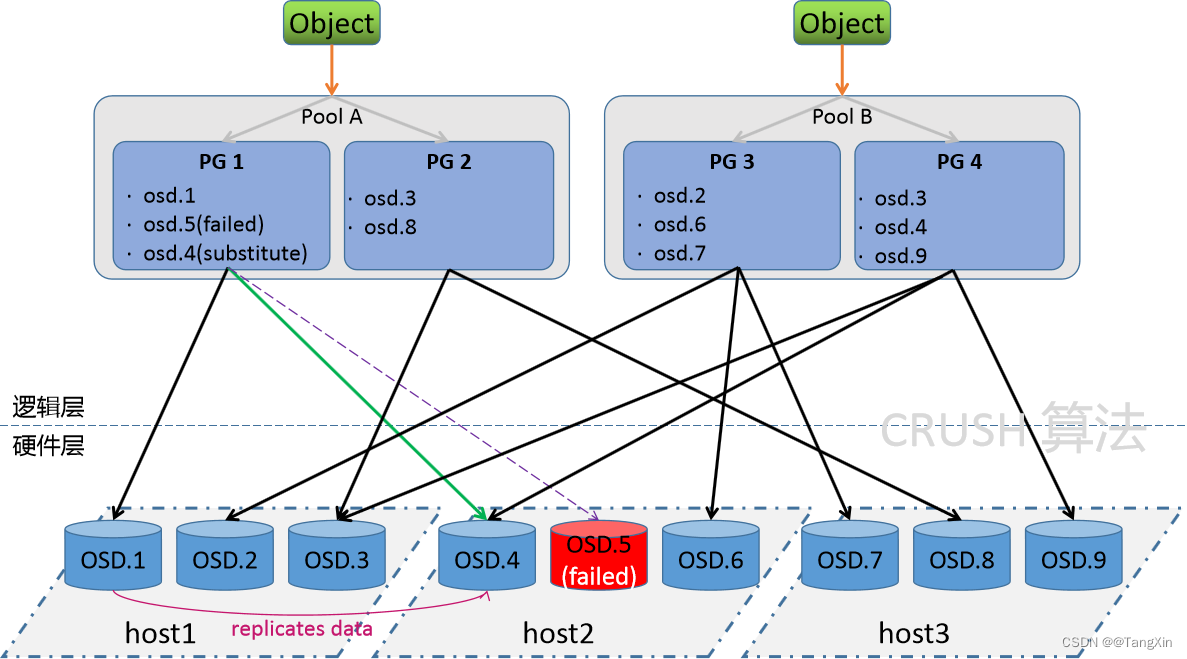
Ceph学习 -4.Ceph组件介绍
文章目录 1.Ceph组件介绍1.1 组件介绍1.2 流程解读1.2.1 综合效果图1.2.2 数据存储逻辑 1.3 小结 1.Ceph组件介绍 学习目标:这一节,我们从组件介绍、流程解读、小结三个方面来学习。 1.1 组件介绍 无论是想向云平台提供 Ceph 对象存储和 Ceph 块设备服务…...
)
Python100个库分享第13个—awesome-slugify(处理Unicode)
目录 专栏导读库的介绍库的安装基础用法1:用‘-’连接基础用法1:汉字转拼音用‘-’连接有个类似的库 —python-slugify安装总结 专栏导读 🌸 欢迎来到Python办公自动化专栏—Python处理办公问题,解放您的双手 🏳️…...

01 SQL基础 -- 初识数据库与安装
一、初识数据库 数据库是将大量数据保存起来,通过计算机加工而成的可以进行高效访问的数据集合。该数据集合称为数据库(Database, DB)。用来管理数据库的计算机系统称为数据库管理系统(Database Management System, DBMS) 1.1 DBMS 的种类 DBMS 主要通过数据的保存格式…...

PyTorch搭建Autoformer实现长序列时间序列预测
目录 I. 前言II. AutoformerIII. 代码3.1 Encoder输入3.1.1 Token Embedding3.1.2 Temporal Embedding 3.2 Decoder输入3.3 Encoder与Decoder3.3.1 初始化3.3.2 Encoder3.3.3 Decoder IV. 实验 I. 前言 前面已经写了很多关于时间序列预测的文章: 深入理解PyTorch中…...
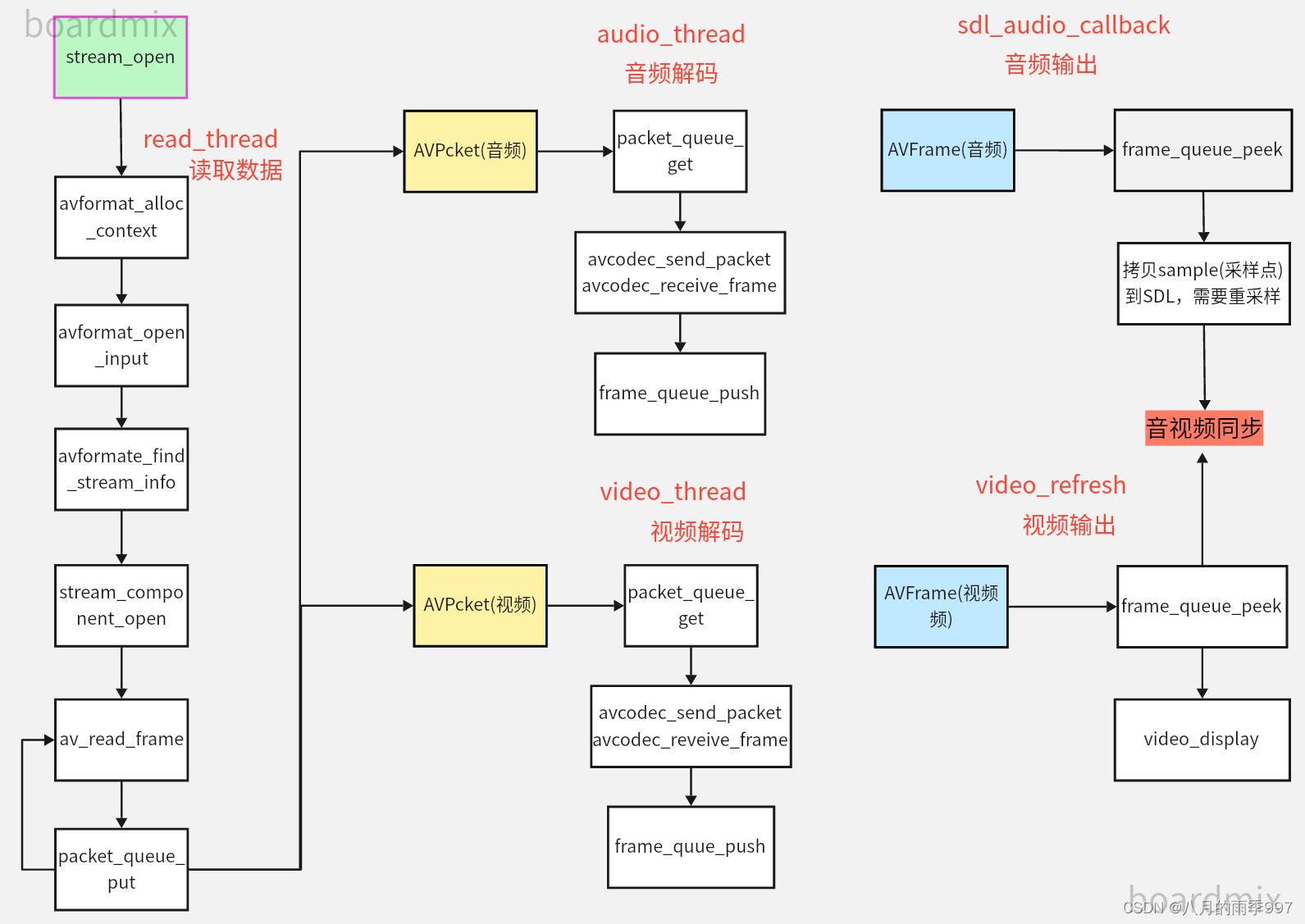
FFmpeg: 简易ijkplayer播放器实现--06封装打开和关闭stream
文章目录 流程图stream openstream close 流程图 stream open 初始化SDL以允许⾳频输出;初始化帧Frame队列初始化包Packet队列初始化时钟Clock初始化音量创建解复用读取线程read_thread创建视频刷新线程video_refresh_thread int FFPlayer::stream_open(const cha…...
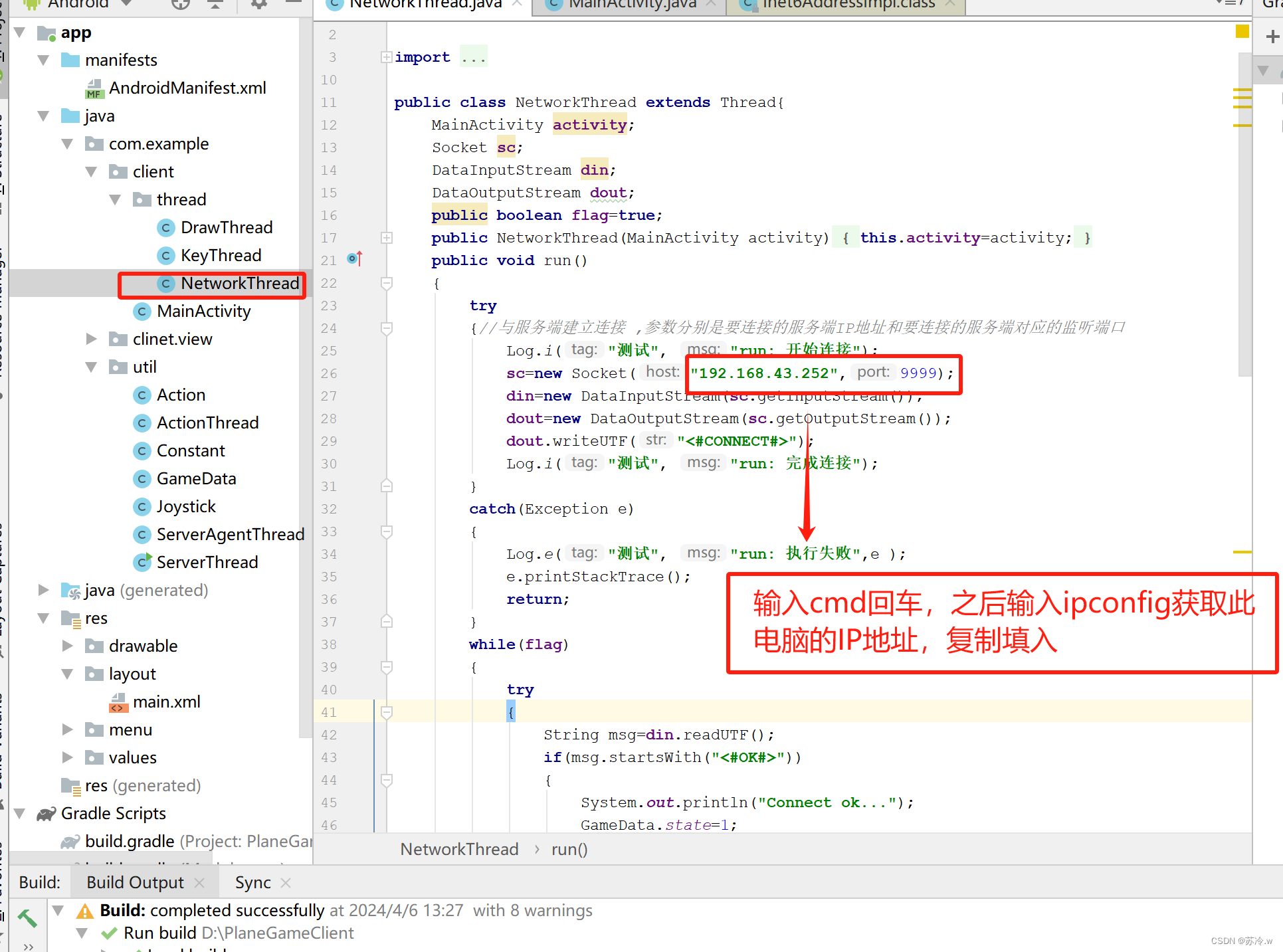
使用Android完成案例教学
目录 题目:完成在Android平台下2个玩家分别利用2个手机连接在同一局域网下通过滑动摇杆分别使红飞机和黄飞机移动的开发。(全代码解析) 题目:完成在Android平台下2个玩家分别利用2个手机连接在同一局域网下通过滑动摇杆分别使红飞…...
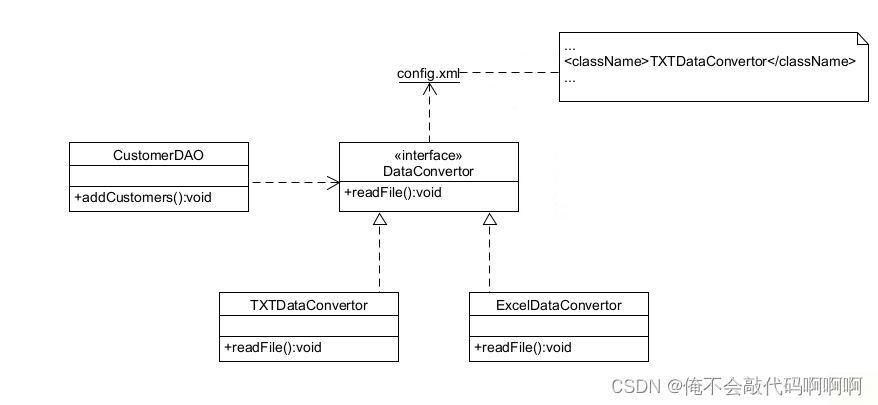
面向对象设计原则实验“依赖倒置原则”
高层模块不应该依赖于低层模块。二者都应该依赖于抽象。抽象不应该依赖于细节。细节应该依赖于抽象。 (开闭原则、里氏代换原则和依赖倒转原则的三个实例很相似,原因是它之间的关系很紧密,在实现很多重构时通常需要同时使用这三个原则。开闭…...
PMP考试到底难在哪里?
虽然PMP考试整体的并没有那么难,通过率也比较高,但PMP考试设计地非常巧妙,所以在面对考试时也不能掉以轻心。 01涉及面广 目前PMP考试内容大部分来源于教材《PMBOK指南》和《敏捷实践指南》。 作为考试出题的知识基础《PMBOK指南》&#x…...

Linux执行命令监控详细实现原理和使用教程,以及相关工具的使用
Linux执行命令监控详细实现原理和使用教程,以及相关工具的使用。 0x00 背景介绍 Linux上的HIDS需要实时对执行的命令进行监控,分析异常或入侵行为,有助于安全事件的发现和预防。为了获取执行命令,大致有如下方法: 遍…...
算法设计与分析实验报告c++实现(生命游戏、带锁的门、三壶谜题、串匹配问题、交替放置的碟子)
一、实验目的 1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握; 2.提高学生利用课堂所学知识解决实际问题的能力; 3.提高学生综合应用所学知识解决实际问题的能力。 二、实验任务 1、 编…...

【电子通识】热风枪的结构与使用方法
热风枪的结构 热风枪是专门用来拆焊、焊接贴片元器件和贴片集成电路的焊接工具,它主要由主机和热风焊枪两大部分构成。 热风枪主要有电源开关、风速设置、温度设置、热风连接等部件组成。根据不同品牌和价位的热风枪,有一些功能齐全的也集成了烙铁功能。…...

mysql知识点
MySQL 中有哪几种锁 表级锁:开销小,加锁快;不会出现死锁;锁定粒度大,发生锁冲突的概率最高,并发度最低。行级锁:开销大,加锁慢;会出现死锁;锁定粒度最小&…...

css Animation 动画-右进左出
transform: rotate(旋转) | scale(缩放) | skew(倾斜) | translate(移动) ;<style> .jinggao {width: 60vw;display: inline-block;text-align: center;overflow: hidden;box-…...
)
第十三届蓝桥杯省赛大学B组填空题(c++)
A.扫雷 暴力模拟AC: #include<iostream> using namespace std; const int N105; int n,m,map[N][N],ans[N][N]; int dx[8]{-1,-1,0,1,1,1,0,-1}; int dy[8]{0,1,1,1,0,-1,-1,-1}; int count(int x,int y){int cnt0;for(int i0;i<8;i){int xxxdx[i];int yyydy[i];if(…...
深耕金融知识领域,助力消费者提升金融素养)
天星金融(原小米金融)深耕金融知识领域,助力消费者提升金融素养
近年来,依托生活和消费品质不断提升的时代契机,信用卡持卡人的数量以及信用卡消费的频率不断增加,信用卡还款问题也日益凸显。部分不法分子打着“智能还款”、“精养提额”的口号“踏浪”入场,实则行诱导、诈骗之实。天星金融&…...
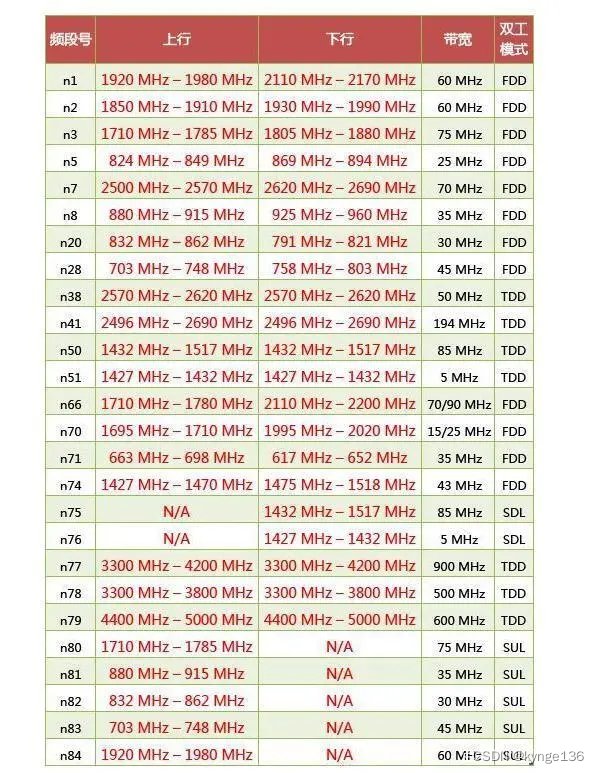
中国手机频段介绍
中国目前有三大运营商,分别是中国移动、中国联通、中国电信,还有一个潜在的运营商中国广电,各家使用的2/3/4G的制式略有不同 中国移动的GSM包括900M和1800M两个频段。 中国移动的4G的TD-LTE包括B34、B38、B39、B40、B41几个频段,…...

企业如何使用SNP Glue将SAP与Snowflake集成?
SNP Glue是SNP的集成技术,适用于任何云平台。它最初是围绕SAP和Hadoop构建的,现在已经发展为一个集成平台,虽然它仍然非常专注SAP,但可以将几乎任何数据源与任何数据目标集成。 我们客户非常感兴趣的数据目标之一是Snowflake。Sno…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

