Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转
738. 单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
思路:
假设这个数是98,n[i]>n[i+1],让n[i]--,n[i+1]=9,即98的单调递增数就是89
如果从前往后遍历,n[i+1]不仅受n[i]影响,还受n[i+2]影响,例如332->329 这时 3又比2大了
如果从后往前遍历,332->329->299,重复利用了上一次的结果
总体来说,从后往前遍历,遇见n[i]<n[i+1]的情况,让n[i]-1,让i+1与之后的位置都变为9

class Solution {public int monotoneIncreasingDigits(int n) {String s=String.valueOf(n);char[] chars=s.toCharArray();int index=s.length();//记录开始填9的位置for(int i=chars.length-2;i>=0;i--){if(chars[i]>chars[i+1]){chars[i]--;index=i+1;}}for(int i=index;i<s.length();i++ ){chars[i]='9';}return Integer.parseInt(String.valueOf(chars));}
}968. 监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
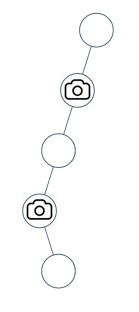
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路:
把摄像头优先放在叶节点的父节点上
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
在二叉树中如何从低向上推导呢?
可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。
如何隔两个节点放一个摄像头?
我们分别有三个数字来表示:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖
遇见空结点怎么办?
空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了

单层递归逻辑:
- 情况1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
- 情况2:左右节点至少有一个无覆盖的情况
如果是以下情况,则中间节点(父节点)应该放摄像头:
- left == 0 && right == 0 左右节点无覆盖
- left == 1 && right == 0 左节点有摄像头,右节点无覆盖
- left == 0 && right == 1 左节点有无覆盖,右节点摄像头
- left == 0 && right == 2 左节点无覆盖,右节点覆盖
- left == 2 && right == 0 左节点覆盖,右节点无覆盖
这个不难理解,毕竟有一个孩子没有覆盖,父节点就应该放摄像头。
此时摄像头的数量要加一,并且return 1,代表中间节点放摄像头。
- 情况3:左右节点至少有一个有摄像头
如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
- left == 1 && right == 2 左节点有摄像头,右节点有覆盖
- left == 2 && right == 1 左节点有覆盖,右节点有摄像头
- left == 1 && right == 1 左右节点都有摄像头
情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况
这时要给根节点加上摄像头
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {int res=0;//摄像头的个数public int minCameraCover(TreeNode root) {if(travel(root)==0)res++;//如果根节点没覆盖,给根节点加摄像头,因为根节点没有父节点return res;}public int travel(TreeNode cur){if(cur==null)return 2;//空结点表示有覆盖int left= travel(cur.left);int right= travel(cur.right);//如果左右都返回覆盖,则当前结点没覆盖if(left==2&&right==2){return 0;}else if(left==0||right==0){//如果左右有任一个没覆盖,则在当前结点加摄像头res++;return 1;} else{//如果左右有任一个有摄像头,则当前结点被覆盖return 2;}}
}80. 翻转
时间限制:1.000S 空间限制:256MB
题目描述
小蓝用黑白棋的 n 个棋子排成了一行,他在脑海里想象出了一个长度为 n 的 01 串 T,他发现如果把黑棋当做 1,白棋当做 0,这一行棋子也是一个长度为 n 的 01 串 S。 小蓝决定,如果在 S 中发现一个棋子和它两边的棋子都不一样,就可以将其翻转变成另一个颜色。也就是说,如果 S 中存在子串 101 或者 010,就可以选择将其分别变为 111 和 000,这样的操作可以无限重复。 小蓝想知道最少翻转多少次可以把 S 变成和 T 一模一样。
输入描述
输入包含多组数据。 输入的第一行包含一个正整数 D 表示数据组数。 后面 2D 行每行包含一个 01 串,每两行为一组数据,第 2i − 1 行为第 i 组 数据的 Ti,第 2i 行为第 i 组数据的 Si,Si 和 Ti 长度均为 ni。
输出描述
对于每组数据,输出一行包含一个整数,表示答案,如果答案不存在请输出 −1。
输入示例
2
1000111
1010101
01000
11000输出示例
2
-1提示信息
对于 20% 的评测用例,1 ≤ ∑D1 ni ≤ 10 ; 对于所有评测用例,保证 1 ≤ ∑D1 ni ≤ 106 ,ni > 0 。
思路:从左往右遍历,遇见不一样的就翻转,注意开头和最后一个是不能翻转的
import java.util.*;
import java.util.stream.Stream;class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();while(n-->0){String s1=in.next();String s2=in.next();System.out.println(solve(s1,s2));}}public static int solve(String s1,String s2){int count=0;for(int i=0;i<s1.length();i++){if(s1.charAt(i)==s2.charAt(i)){continue;}else{if(i==0||i==s2.length()-1||s2.charAt(i)==s2.charAt(i-1)||s2.charAt(i)==s2.charAt(i+1)){return -1; }count++;}}return count;}}
相关文章:

Day37:LeedCode 738.单调递增的数字 968.监控二叉树 蓝桥杯 翻转
738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9 思路: 假设这个数是98,…...

详解Qt元对象系统
Qt库作为一款流行的跨平台C应用程序开发框架,其中的元对象系统是其核心特性之一。Qt元对象系统不仅提供了诸如信号槽(Signals & Slots)、属性系统(Property System)等功能,还实现了对C对象的运行时类型…...

无法用raven-js,如何直接使用TraceKit标准化错误字符串(一次有趣的探索)
引子:网上三年前(2020)的文章介绍了一个raven-js 简单说就是把堆栈信息格式化兼容各浏览器,便于查看错误来源。 **but:**到处找了一下raven-js,已经没有官方出处了,只在Sentry的源码仓库里发现…...

Docker学习笔记(二):在Linux中部署Docker(Centos7下安装docker、环境配置,以及镜像简单使用)
一、前言 记录时间 [2024-4-6] 前置文章:Docker学习笔记(一):入门篇,Docker概述、基本组成等,对Docker有一个初步的认识 在上文中,笔者进行了Docker概述,介绍其历史、优势、作用&am…...

uniapp 检查更新
概览 在uniapp中检查并更新应用,可以使用uni-app自带的更新机制。以下是一个简单的示例代码,用于在应用启动时检查更新: // 在App.vue或者其他合适的地方调用 onLaunch: function() {// 当uni-app初始化完成时执行// 判断平台const platfor…...
数据结构——正则表达式)
(Java)数据结构——正则表达式
前言 本博客是博主用于复习数据结构以及算法的博客,如果疏忽出现错误,还望各位指正。 正则表达式概念 正则表达式,又称规则表达式(Regular Expression),是一种文本模式,包括普通字符…...
第6章 6.3.1 正则表达式的语法(MATLAB入门课程)
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 正则表达式可以由一般的字符、转义字符、元字符、限定符等元素组…...
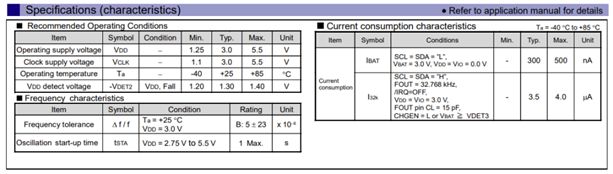
RX8130CE为用户提供带复位延迟和主备电管理的解决方案
实时时钟作为设备的精确时钟来源,其作用如同人的心脏,为设备提供准确稳定的心跳.而便携式设备由于应用场景多变,所以对内部元器件要求也相对较高,这就对作为核心器件的实时时钟模块提出不少挑战。EPSON实时钟模块产品线拥有丰富的…...

JS文件导出变量
如果 config.js 文件中有多个变量要导出,你可以按照以下步骤进行: 1. 在 config.js 文件中定义多个变量,并使用 export 导出它们。 // config.js const baseUrl "http://localhost:8081"; const apiKey "your_api_key&quo…...

已知私钥和密文,如何用python进行RSA解密
要使用Python进行RSA解密,你可以使用pycryptodome库。下面是一个简单的示例,展示了如何使用已知的私钥和密文进行RSA解密: 首先,确保你已经安装了pycryptodome库。如果没有安装,你可以通过运行pip install pycryptodome来安装它。 然后,你可以使用以下代码进行RSA解密:…...

vue2-vue3面试
v-text/v-html/v-once/v-show/v-if/v-for/v-bind/v-on beforeCreate() 已有DOM节点:可以data选项:不可以虚拟DOM节点:不可以 created():掌握 已有DOM节点:可以data选项:可以虚拟DOM节点:不可以 beforeMount…...

jmeter生成随机数的详细步骤及使用方式
Apache JMeter 是一个用于测试性能的开源工具,它可以模拟多种类型的负载并测量应用程序的性能。在 JMeter 中生成随机数可以通过使用预定义的函数来实现。以下是生成随机数的详细步骤及使用方式: 安装 JMeter: 首先,你需要在你的计…...

速盾:为什么会出现高防cdn?它适合哪些行业?
随着互联网的不断发展和普及,网络安全问题也变得日益突出。由于互联网的特性,许多企业和组织的在线业务往往面临来自网络攻击的威胁,如DDoS攻击、恶意爬虫等。为了保护在线业务的正常运行和用户数据的安全,高防CDN应运而生。 高防…...

GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南
GB∕T 25058-2019 信息安全技术 网络安全等级保护实施指南...
使用Nodejs + express连接数据库mongoose
文章目录 先创建一个js文档安装 MongoDB 驱动程序:引入 MongoDB 模块:设置数据库连接:新建一个表试试执行数据库操作:关闭数据库连接: 前面需要准备的内容可看前面的文章: Express框架搭建项目 node.js 简单…...

朗致集团面试-Java架构师
总结 三轮面试,第一轮是逻辑测试性格测试,第二轮是技术面试(面试官-刘老师),第三轮是CTO面试(面试官-屠老师)。如果第三轮面试通过,考官会问你薪资意向,如果满意的话HR就…...

Ubuntu 23.10 搜狗拼音输入法闪屏解决
问题与解决 Ubuntu 23.10下安装搜狗拼音输入法并且使用搜狗输入法时,会闪屏。站内有人说可以换使用Xorg作为桌面服务,然后使用基于X11的桌面,其实可以不用那么麻烦,只需要设置QT的环境变量QT_QPA_PLATFORMxcb,然后重新…...
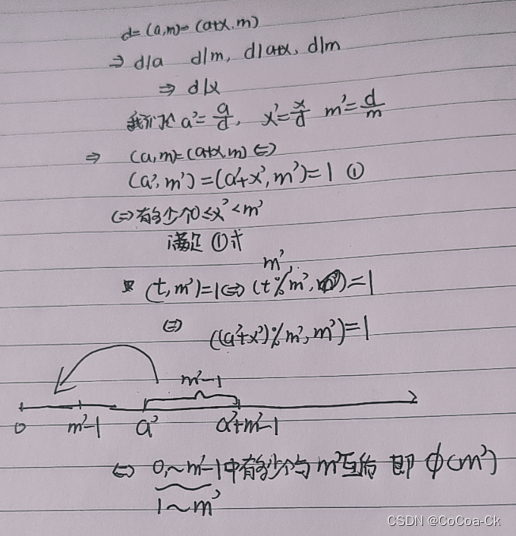
备战蓝桥杯---刷杂题2
显然我们直接看前一半,然后我们按照斜行看,我们发现斜行是递增的,而同一行从左向右也是递增的,因此我们可以直接二分,同时我们发现对称轴的数为Ck,2k. 我们从16斜行枚举即可 #include<bits/stdc.h> using name…...
.[[backup@waifu.club]].svh勒索病毒数据怎么处理|数据解密恢复
尊敬的读者: 近年来,随着信息技术的迅猛发展,网络安全问题日益凸显,其中勒索病毒成为了一大威胁。.[[backupwaifu.club]].svh、.[[MyFilewaifu.club]].svh勒索病毒就是其中之一,它以其独特的传播方式和恶劣的加密手段…...
)
SpringFramework实战指南(八)
SpringFramework实战指南(八) 5.1 场景设定和问题复现5.2 解决技术代理模式5.1 场景设定和问题复现 准备AOP项目 项目名:spring-aop-annotation pom.xml <dependencies><!--spring context依赖--><!--当你引入Spring Context依赖之后,表示将Spring的基础依赖…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
