相机模型浅析
相机模型
文章目录
- 相机模型
- 四个坐标系
- 针孔相机模型
- 世界坐标系到相机坐标系
- 相机坐标系到图像坐标系
- 图像坐标到像素坐标
四个坐标系
①世界坐标系:是客观三维世界的绝对坐标系,也称客观坐标系。因为数码相机安放在三维空间中,我们需要世界坐标系这个基准坐标系来描述数码相机的位置,并且用它来描述安放在此三维环境中的其它任何物体的位置,用 ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw)表示其坐标值。
②相机坐标系(光心坐标系):以相机的光心为坐标原点,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,相机的光轴为Z 轴,用 ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc,Yc,Zc)表示其坐标值。
③图像坐标系:以CCD 图像平面的中心为坐标原点,X轴和Y 轴分别平行于图像平面的两条垂直边,用 ( x , y ) ( x , y ) (x,y)表示其坐标值。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
④像素坐标系:以 CCD 图像平面的左上角顶点为原点,X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴,用 ( u , v ) (u , v ) (u,v)表示其坐标值。
针孔相机模型
相机实质上就是完成一个3D空间到2D平面的投影的过程其中投影中心称为摄像机中心 ,也称为光心摄像机中心到图像平面的垂线称为摄像机的主轴或主射线 ,而主轴在图像平面的交点称为主点。过摄像机中心平行于图像平面的平面称为摄像机的主平面。

世界坐标系到相机坐标系

一般, 空间点采用不同的欧氏坐标系表示 ,称为世界坐标系。其中世界坐标系于相机坐标系通过旋转和平移相联系
因为可以将相机坐标系看作世界坐标系的一个欧式变换,设一个点 A A A在世界坐标系中的坐标为 [ X w , Y w , Z w , 1 ] T [X_w,Y_w,Z_w,1]^T [Xw,Yw,Zw,1]T,在相机坐标系中的坐标为 [ X c , Y c , Z c , 1 ] T [X_c,Y_c,Z_c,1]^T [Xc,Yc,Zc,1]T,则存在以下关系
[ X c Y c Z c 1 ] = [ R t 0 T 1 ] [ X w Y w Z w 1 ] \begin{bmatrix} X_c\\ Y_c\\ Z_c\\ 1 \end{bmatrix}= \begin{bmatrix} R&t\\ 0^T&1 \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\\ Z_w\\ 1 \end{bmatrix} XcYcZc1 =[R0Tt1] XwYwZw1
其中 R , t R,t R,t称为相机的外部参数,并将 [ R t 0 T 1 ] \begin{bmatrix} R&t\\ 0^T&1 \end{bmatrix} [R0Tt1]即为 M e x t M_{ext} Mext
相机坐标系到图像坐标系
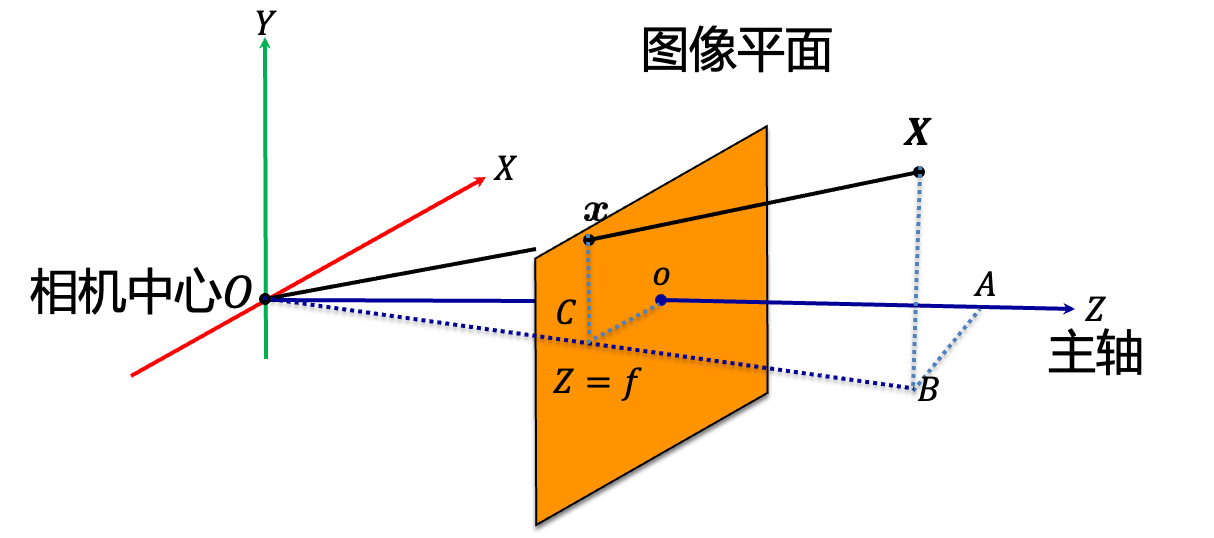
根据相似三角形可得 ∥ O C ∥ ∥ A B ∥ = ∥ O O ∥ ∥ O A ∥ = ∥ O C ∥ ∥ O B ∥ = ∥ x C ∥ ∥ X B ∥ \frac{\|OC\|}{\|AB\|}=\frac{\|OO\|}{\|OA\|}=\frac{\|OC\|}{\|OB\|}=\frac{\|xC\|}{\|XB\|} ∥AB∥∥OC∥=∥OA∥∥OO∥=∥OB∥∥OC∥=∥XB∥∥xC∥
可得在相机坐标系中的点 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc)在图像平面上的投影为 ( f X c Z c , f Y c Z c ) (f\frac{X_c}{Z_c},f\frac{Y_c}{Z_c}) (fZcXc,fZcYc),其中在齐次坐标中表示为 ( f X c , f Y c , Z c ) (fX_c,fY_c,Z_c) (fXc,fYc,Zc)
可构造方程
[ f X c f Y c Z c ] = [ f 0 f 0 1 0 ] [ X c Y c Z c 1 ] \begin{bmatrix} fX_c\\ fY_c\\ Z_c \end{bmatrix} =\begin{bmatrix}f&&&0\\&f&&0\\&&1&0\end{bmatrix}\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix} fXcfYcZc = ff1000 XcYcZc1
其中矩阵 [ f 0 f 0 1 0 ] \begin{bmatrix} f&&&0\\ &f&&0\\ &&1&0 \end{bmatrix} ff1000 记为 M p r o j M_{proj} Mproj
图像坐标到像素坐标
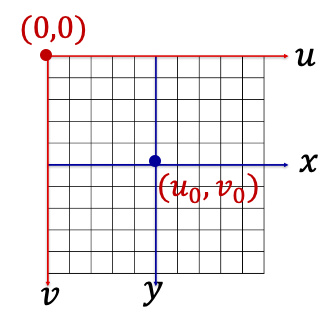
可得以下关系
[ u v 1 ] = [ k u 0 l v 0 1 ] [ x y 1 ] \begin{bmatrix} u\\ v\\ 1 \end{bmatrix} =\begin{bmatrix} k&&u_0\\ &l&v_0\\ &&1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} uv1 = klu0v01 xy1
其中 k k k和 l l l分别是每个像素在图像平面x和 y方向上的物理尺寸。
其中将矩阵 [ k u 0 l v 0 1 ] \begin{bmatrix} k&&u_0\\ &l&v_0\\ &&1 \end{bmatrix} klu0v01 记为 M a f f M_{aff} Maff

若 u , v u,v u,v不垂直,其夹角为 θ \theta θ。则 M a f f = [ k − k cos θ u 0 l / sin θ v 0 1 ] M_{aff}=\begin{bmatrix} k&-k\cos\theta&u_0\\ &l/\sin\theta&v_0\\ &&1 \end{bmatrix} Maff= k−kcosθl/sinθu0v01
相关文章:

相机模型浅析
相机模型 文章目录 相机模型四个坐标系针孔相机模型世界坐标系到相机坐标系相机坐标系到图像坐标系图像坐标到像素坐标 四个坐标系 ①世界坐标系:是客观三维世界的绝对坐标系,也称客观坐标系。因为数码相机安放在三维空间中,我们需要世界坐标…...
国芯科技(C*Core)双芯片汽车安全气囊解决方案
汽车安全气囊是20世纪汽车上的十大发明之一,是目前汽车的法定标准配置,成为汽车驾乘人员生命安全的保护神。随着人们对汽车安全性要求的进一步提高,已形成前排驾驶员气囊、前排副驾驶员气囊、前排侧气囊、后排侧气囊、膝部气囊、安全气帘等等…...

牛客周赛 Round 39(A,B,C,D,E,F,G)
比赛链接 官方题解(视频) B题是个贪心。CD用同余最短路,预处理的完全背包,多重背包都能做,比较典型。E是个诈骗,暴力就完事了。F是个线段树。G是个分类大讨论,出题人钦定的本年度最佳最粪 题目…...

解锁区块链技术的潜力:实现智能合约与DApps
在数字时代,区块链技术正迅速成为重塑多个行业的革命性力量。从金融服务到供应链管理,再到数字身份验证,区块链提供了一种去中心化、安全和透明的数据处理方式。在本文中,我们将深入探讨区块链技术,特别是智能合约和去…...

MAC OS关闭SIP(navicat 无法保存密码)
最近安装navicat(16.3.7)时,安装后无法保存密码,保存密码会报错如下: 因为用的破解版,一开始是打不开的,用自带的修复软件修复后就可以打开了,但是保存密码就会报错,按照网上的一些操作 1、卸载…...

阿里云服务器带宽价格全解析,附报价单
阿里云服务器公网带宽怎么收费?北京地域服务器按固定带宽计费一个月23元/M,按使用流量计费0.8元/GB,云服务器地域不同实际带宽价格也不同,阿里云服务器网aliyunfuwuqi.com分享不同带宽计费模式下带宽收费价格表: 公网…...
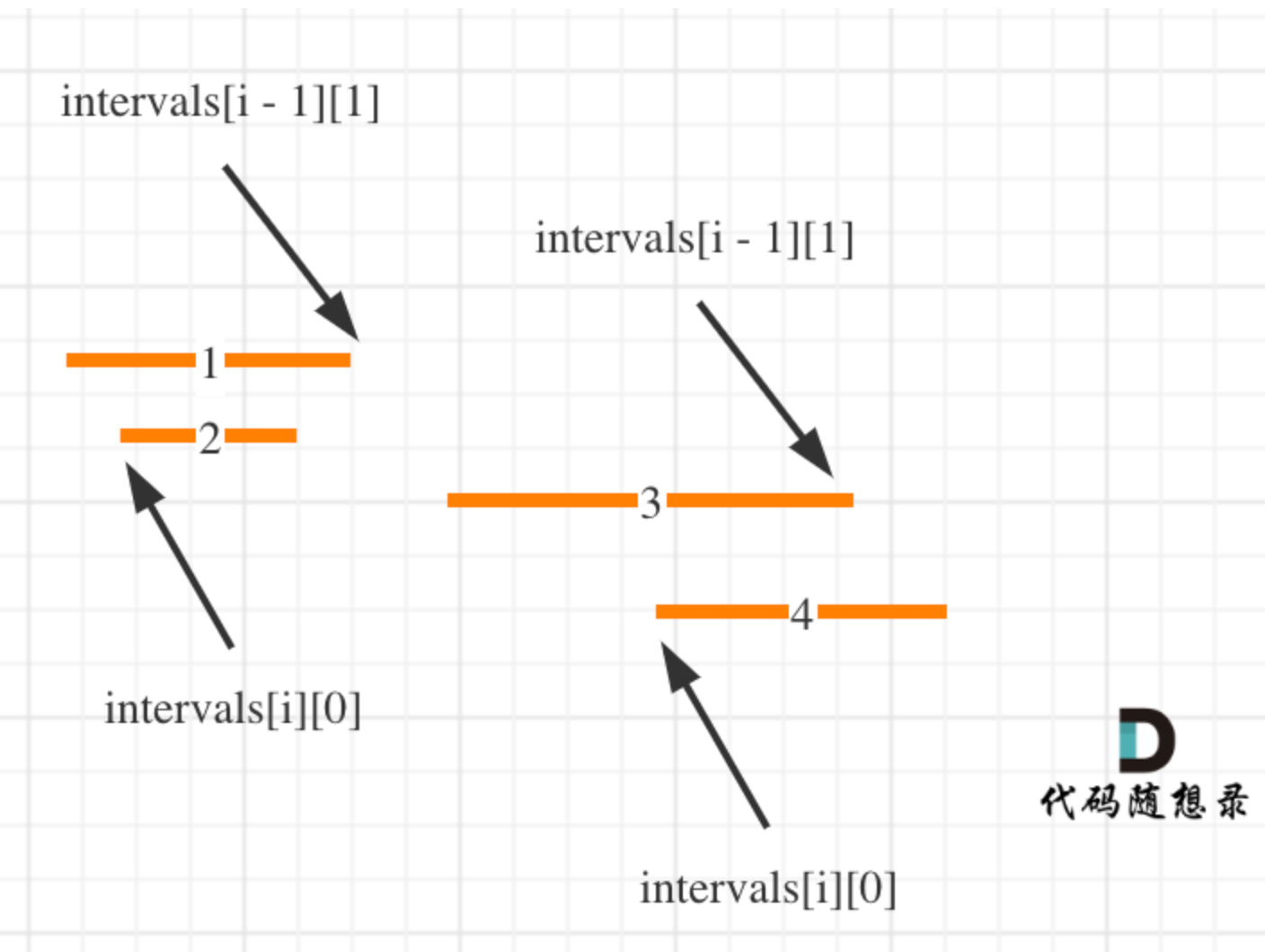
Day36|贪心算法part05:435. 无重叠区间、763.划分字母区间、56. 合并区间
435. 无重叠区间 有了上题射气球的因子,这题也就有思路了,反正无脑排序就行了: 首先将所有区间按照end的大小从小到大排序;选取最早end为起始x_end遍历所有区间,如果该区间的start比end大(可重叠…...

棋牌室计时吧台计费收费灯控管理系统软件操作流程
棋牌室计时吧台计费收费灯控管理系统软件操作流程 一、前言 以下软件操作教程以,佳易王棋牌桌球计时计费管理系统软件灯控版V17.87为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 该计时计费软件可以是棋牌和桌球混合同时计时计费 …...

【实践篇】RabbitMQ实现队列延迟功能汇总
前言 记录下RabbitMQ实现延迟队列功能的所有实践内容。 前期准备,需要安装好docker、docker-compose的运行环境。 一、安装RabbitMQ 开启RabbitMQ的WEB管理功能。-CSDN博客 二、实现延迟队列的两种方式 RabbitMQ实现延迟队列的两种方式。-CSDN博客 三、实践文…...

EditPlus来啦(免费使用!)
hello,我是小索奇 今天推荐一款编辑器,是索奇学习JavaSE时入手滴,非常好用哈,小索奇还是通过老杜-杜老师入手滴,相信很多人也是通过老杜认识嘞,来寻找破解版或者准备入手这个间接使用的编辑器~ EditPlus是…...

蓝桥杯22年第十三届省赛-数组切分|线性DP
题目链接: 蓝桥杯2022年第十三届省赛真题-数组切分 - C语言网 (dotcpp.com) 1.数组切分 - 蓝桥云课 (lanqiao.cn) 这道题C语言网数据会强一些。 说明: 对于一个切分的子数组,由于数组是1-N的一个排列,所以每个数唯一 可以用子…...
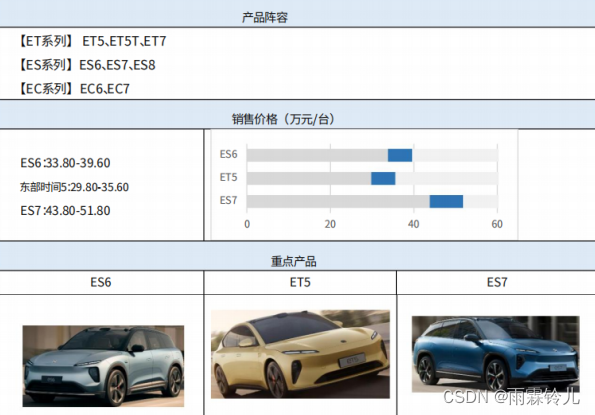
小米汽车:搅动市场的鲶鱼or价格战砧板上的鱼肉?
3月28日晚,备受关注的小米汽车上市发布会召开,小米集团董事长雷军宣布小米SU7正式发布。小米汽车在带飞股价的同时,二轮订购迅速售尽。 图一:小米集团股价 雷军口中“小米汽车迈出的第一步,也是人生最后一战的开篇”&a…...

Docker 学习笔记(五):梳理 Docker 镜像知识,附带 Commit 方式提交镜像副本,安装可视化面板 portainer
一、前言 记录时间 [2024-4-10] 前置文章: Docker学习笔记(一):入门篇,Docker概述、基本组成等,对Docker有一个初步的认识 Docker学习笔记(二):在Linux中部署Docker&…...
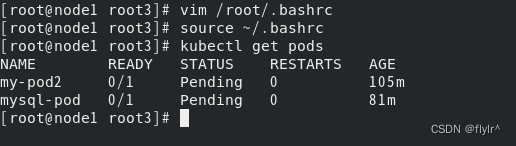
K8S node节点执行kubectl get pods报错
第一个问题是由第二个问题产生的,第二个问题也是最常见的 网上找的都是从master节点把文件复制过来,这样确实可以解决,但是麻烦,有一个node节点还好,如果有多个呢?每个都复制吗?下面是我从外网…...

C++简单日志系统
需求描述 日志等级:定义一个枚举类型 LogLevel,包含至少四个等级:DEBUG、INFO、WARNING、ERROR。日志记录:实现一个 Logger 类,包含以下功能: 一个静态方法 log,接受 LogLevel 和一个字符串作为…...

MySQL基础练习题:习题21-25
这部分主要是为了帮助大家回忆回忆MySQL的基本语法,数据库来自于MySQL的官方简化版,题目也是网上非常流行的35题。这些基础习题基本可以涵盖面试中需要现场写SQL的问题。 列出在部门sales工作的员工的姓名,假定不知道销售部的部门编号 sele…...

全面的网络流量监控
流量监控指的是对数据流进行的监控,通常包括出数据、入数据的速度、总流量。通过网络流量监控,组织可以确保只有业务关键型流量通过网络传输,并限制不需要的网络流量,从而提高网络效率,又可以防止停机、减少 MTTR、帮助…...

探索网络爬虫:技术演进与学习之路
网络爬虫及IP代理池 前言爬虫技术的演进最新的爬虫技术爬虫技术学习路线 前言 在信息时代,网络爬虫技术作为获取和处理网络数据的重要手段,已经成为数据科学、机器学习和许多商业应用的基石。从简单的HTML页面抓取到复杂的动态内容采集,爬虫…...

目标检测——色素性皮肤病数据集
一、重要性及意义 首先,色素性皮肤病变是一类常见的皮肤疾病,其发病率有逐年增高的趋势。这些病变可能由遗传或环境因素导致黑素细胞生成异常,如黑色素瘤等。黑色素瘤具有极高的恶性率和致死率,而且恶化可能性大,容易…...

Unity3D 打空包与远程资源更新详解
前言 在游戏开发过程中,打包和远程资源更新是非常重要的步骤,本文将详细介绍Unity3D中如何进行打空包和远程资源更新。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! 一、打空包 …...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
