代码随想录算法训练营第三十八天| 509. 斐波那契数,70. 爬楼梯,746. 使用最小花费爬楼梯
题目与题解
参考资料:动态规划基础
动态规划五步曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
题目链接:509. 斐波那契数
代码随想录题解:509. 斐波那契数
视频讲解:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
解题思路:
斐波那契数是最经典的递归/迭代题,迭代方法对应的就是动态规划。
已知F(0), F(1)以及F(n) = F(n-1)+F(n-2),直接就可以用循环逐一写出F(n)的值了。这里因为不需要求1-n之间每个数的斐波那契数,所以简单一点,不用数组记录结果,只要用临时变量记录F(n-1)和F(n-2)即可。
class Solution {public int fib(int n) {if (n <= 1) return n;int pre1 = 0, pre2 = 1;int cur = 0;for (int i = 2; i < n; i++) {cur = pre1 + pre2;pre1 = pre2;pre2 = cur;}return cur;}
}看完代码随想录之后的想法
按照随想录的五步法做练习:
- 确定dp数组(dp table)以及下标的含义:dp[i]表示数i的斐波那契数
- 确定递推公式:题目已经给了,dp[i]=dp[i-1]+dp[i-2]
- dp数组如何初始化:同样题目已经给了,dp[0] = 0, dp[1] = 1
- 确定遍历顺序:当前数的斐波那契数由其前两个数相加直接得到,所以按顺序遍历即可
- 举例推导dp数组:随意用一串斐波那契数带入递推公式 - 0,1,1,2,3,5,8...,符合要求
遇到的困难
无
70. 爬楼梯
题目链接:70. 爬楼梯
代码随想录题解:70. 爬楼梯
视频讲解:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
解题思路:
这题其实其实就是求斐波那契数的变种,因为爬到当前楼梯的方法,要么是从前一个楼梯爬一级,要么是从再前一个楼梯爬两级,除此之外没有别的选择了,所以递推公式仍然是F(n) = F(n-1)+F(n-2),不一样的地方在于初始值,第一个数F(1)=1,第二个数F(2)=2。
class Solution {public int climbStairs(int n) {if (n <= 2) return n;int[] dp = new int[]{1, 2};int res = 0;for (int i = 3; i <= n; i++) {res = dp[0] + dp[1];dp[0] = dp[1];dp[1] = res;}return res;}
}看完代码随想录之后的想法
附上拓展题,一次最多可以爬m个台阶
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) { // 把m换成2,就可以AC爬楼梯这道题if (i - j >= 0) dp[i] += dp[i - j];}}return dp[n];}
};遇到的困难
无
746. 使用最小花费爬楼梯
题目链接:746. 使用最小花费爬楼梯
代码随想录题解:746. 使用最小花费爬楼梯
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯_哔哩哔哩_bilibili
解题思路:
这题比普通爬楼梯略复杂了一些,除了一次可以爬一步或者两步的基础要求外,还有需要花费最小代价,所以爬楼梯时哪些台阶走一步,哪些台阶走两步,就涉及到了选择的问题。但是,这里还是可以抽象化为动态规划去做,用dp[i]记录爬到当前台阶所需的最小花费,那么dp[i]要么是从dp[i-1]走一步得到,要么是从dp[i-2]走两步得到,所以dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])。
这里需要注意一下,爬上第0级和第1级台阶是不需要代价的,所以初始化dp[0]=dp[1]=0。
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[]{0, 0};int sum = 0;for (int i = 2; i <= cost.length; i++) {sum = Math.min(dp[1] + cost[i - 1], dp[0] + cost[i - 2]);dp[0] = dp[1];dp[1] = sum;}return dp[1];}
}看完代码随想录之后的想法
思路是一样的,这题同样不难,不严格按照五步分析也能写出来。但是后面题目变难了就不好说了。
遇到的困难
一开始初始化dp[0]和dp[1]的时候写成了cost[0]cost[1],怎么着都不对,然后就用了一个数列举例,逐一写出如何得到dp[i]的结果,然后才意识到第0,1级台阶不需要cost就可以上去。所以做错的时候直接举例最直观。
今日收获
初步学习了动态规划方法的五部曲,用简单题实践了一下,目前感觉尚可。
相关文章:

代码随想录算法训练营第三十八天| 509. 斐波那契数,70. 爬楼梯,746. 使用最小花费爬楼梯
题目与题解 参考资料:动态规划基础 动态规划五步曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 题目链接:509. 斐波那契数 代码随想录题解&am…...
视频中会动的进度条
视频中会动的进度条 1.成果展示:2.步骤: 1.成果展示: 2.步骤:...
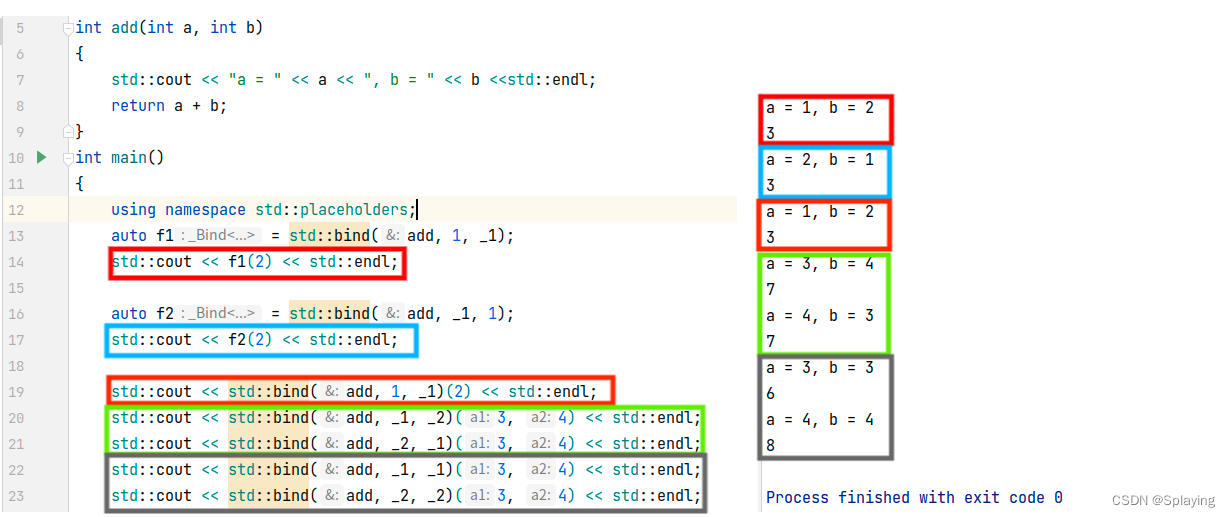
C++高级特性:柯里化过程与std::bind(六)
1、柯里化过程 1.1、operator()的引入 现在需要完成这样一个需求:有一个函数每次调用返回的结果不一样。例如:两次调用的返回值都不一样那么就可以达到这种目的 1.1.1、简单点的写法 可以给一个全局的变量(静态变量)ÿ…...
vmware虚拟机补救
更新了虚拟机里面工具和资料,进行了磁盘整理和压缩,虚拟机运行进不去系统了。 网站找的修复方法均不可行。补救措施:利用DiskGenius.exe(要用高版本不然复制的时候就知道了) DG1342.rar - 蓝奏云 加载虚拟硬盘 2008x…...

数据结构(算法)
总结,建议看EXCEL的《算法》页签,不然感觉有点乱 备注原理/步骤时间复杂度空间复杂度串的应用模式匹配简单/暴力O(mn) KMP O(mn) 树的应用树哈夫曼树1、带权路径长度WPL 2、外部排序-最佳归并树1、哈夫曼树的度,只有0和m(m叉…...
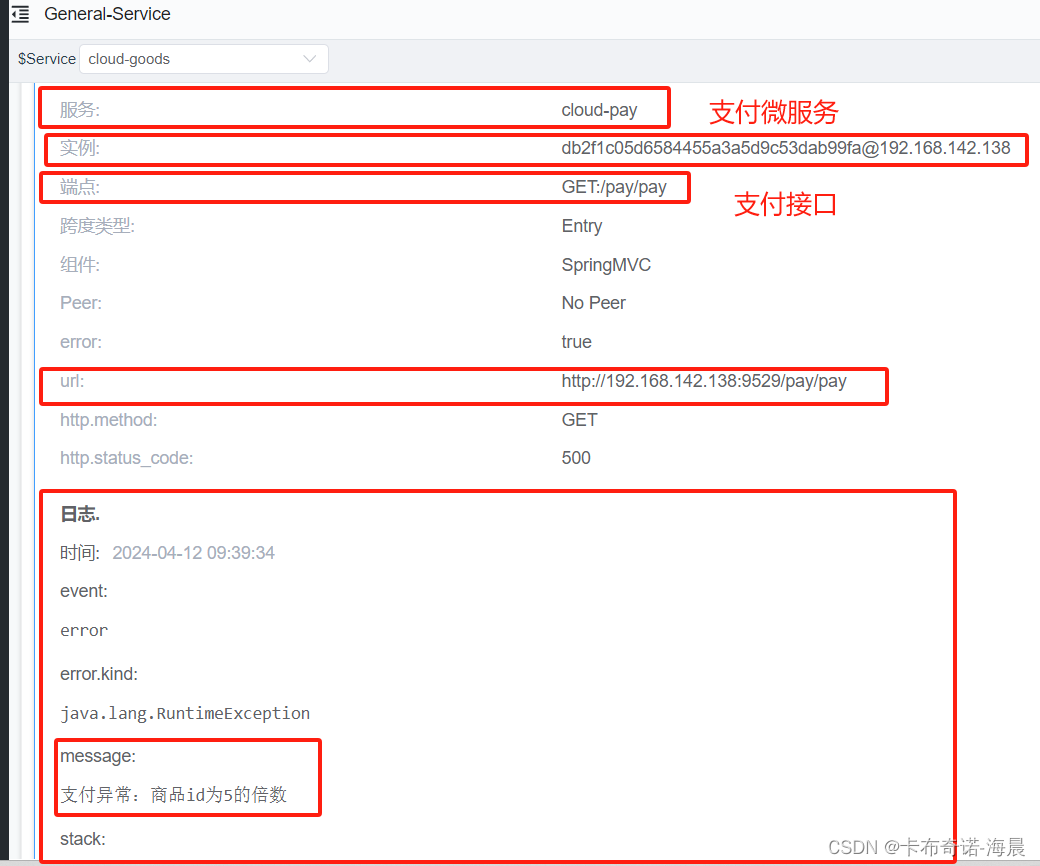
SpringCloud集成SkyWalking链路追踪并收集日志2
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

纯小白蓝桥杯备赛笔记--DAY4(数学数据结构图论)
文章目录 数学质因数分解辗转相除法求最大公约数最小公倍数:快速幂乘法逆元费马小定理 逆元乘法逆元素数判定与埃式筛法朴素素数判定法埃式筛法 图论并查集T3:真题--合根植物DijkstraFloyd 基础算法递归,循环,前缀和,差分STL 数学…...

python 最简单的网页爬虫
import requests url"https://news.ifeng.com/c/8OZc7eV01sM" rrequests.get(url) print(r.status_code) print(r.iter_lines()) # 获取响应的内容 content r.text# 打印网页内容 print(content) # responser.json() # print(response) 爬虫知识讲解: …...

二叉树-数据结构
二叉树-数据结构 二叉树是属性结构的一个重要类型。 如下图二叉树形状 二叉树特征如下: 1.二叉树由 n(n > 0) 个节点组成 2.如果 n 为 0,则为空树 3.如果 n 1,则只有一个节点称为根节点(root) 4.每个节点最多有两个节点,节…...

ansible使用shell模块的环境变量问题
在本机写了一个shell脚本,关于操作mysql的,在本机执行脚本可以正常操作数据库,脚本运行正常。 但是使用ansible ansible -i ./hosts test_teledb -m copy -a "src/etc/ansible/scripts/check.sh dest/tmp"ansible -i ./hosts test…...

ChatGPT论文写作指南:写出引人注目的论文
ChatGPT无限次数:点击直达 ChatGPT论文写作指南:写出引人注目的论文 作为一名有着10年经验的专业CSDN网站原创文章优质创作者,在当今的信息爆炸时代,论文写作的重要性愈发显现。如何能够写出引人注目的论文,吸引读者的眼球并获得…...
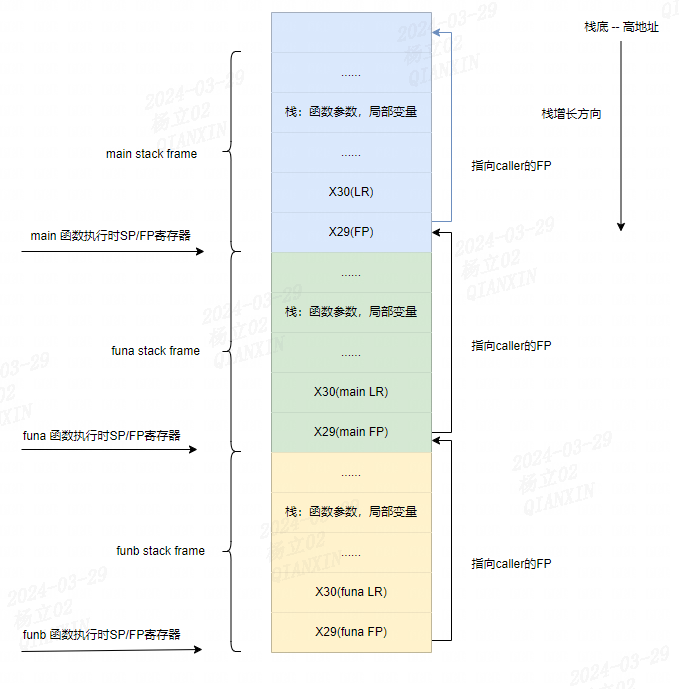
ARM64架构栈帧回溯
文章目录 前言一、栈帧简介二、demo演示 前言 请参考:ARM64架构栈帧以及帧指针FP 一、栈帧简介 假设下列函数调用: funb() {func() }funa() {funb() }main() {funa() }main函数,funa函数,funb函数都不是叶子函数,其…...
-- 基础知识)
LangChain:大型语言模型(LLMs)-- 基础知识
1、LangChain的调用大型语言模型模块的介绍 LangChain是一个强大的框架,旨在通过调用大型语言模型(LLM)来开发各种语言驱动的应用程序。在LangChain中,LLM不仅仅是一个简单的模型调用,而是一个复杂链条中的关键部分。…...

总分410+专业130+国防科技大学831信号与系统考研经验国防科大电子信息与通信工程,真题,大纲,参考书。
好几个学弟催着,总结一下我自己的复习经历,希望大家复习少走弯路,投入的复习正比换回分数。我专业课831信号与系统130(感觉比估分要低,后面找Jenny老师讨论了自己拿不准的地方也没有错误,心里最近也这经常回…...

chatgpt Team 4.0共享合租账号的新方式
为了更好地满足工作需求,我订阅了GPT PLUS会员,但我发现,4.0每三小时问答40次经常吃灰,而且每月近200元的费用让我感到有点肉痛。 于是,我开始寻找有没有什么替代品。在逛某论坛的时候,发现了一个共享Team…...

类和对象二
一、运算符重载 为了使自定义类型可以使用加减等运算符,CPP提供了一个功能叫运算符重载。 关键字:operator操作符 运算符重载最好定义在类对象里,这也可以避免访问不到私有成员的问题。 代码演示: 在类里定义之后,…...

GD32 HID键盘矩阵键盘发送数据时,一直发送数据问题处理
这个问题找了两三天,开始并不认为是示例程序的问题,只是感觉是自己代码问题。 这个解决流程大概是: 先调好矩阵键盘=> 调用发送函数。 就是因为调用时,一直发送数据,我也在按键抬起做了操作,始终不行。 最后,发现时示例代码中有个 空闲中断 引起的。 udev->reg…...

小程序地理位置权限申请+uniapp调用uni.getLocation
文章目录 一、小程序地理位置权限申请二、uniapp调用uni.getLocation 一、小程序地理位置权限申请 需要确保小程序类目已经填写 点击左侧导航栏找到最后的“设置”——“基本设置”——“前往填写” 在开发管理——接口设置——地理位置中可以看到: 即可点击想要申…...

后台权限控制及动态路由
需求 后台系统需要能实现不同的用户权限可以看到不同的功能。 用户只能使用他的权限所允许使用的功能。 功能设计 之前在我的SpringSecurity的课程中就介绍过RBAC权限模型。没有学习过的可以去看下 RBAC权限模型 。这里我们就是在RBAC权限模型的基础上去实现这个功能。 表分…...

云计算:Linux 部署 OVS 集群(控制端)实现OpenFlow
目录 一、实验 1.环境 2.Linux 部署 OVS 集群(控制端) 3.控制端对接服务端OVS网元 4.服务端OVS添加流表 5.服务端删除OVS 二、问题 1. ODL如何查找已安装插件 2.查看流表显示不全 3.如何删除OVS流表 一、实验 1.环境 (1) 主机 表1 宿主机 主…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
