时间序列分析 # 平稳性检验和ARMA模型的识别与定阶 #R语言
- 掌握单位根检验的原理并能解读结果;
- 掌握利用序列的自相关图和偏自相关图识别模型并进行初步定阶。
原始数据在文末!!!
练习1、根据某1971年9月-1993年6月澳大利亚季度常住人口变动(单位:千人)的数据(行数据)(题目1数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
data1 <- scan("F:/时间序列分析/实验5/习题数据/题目1数据.txt")
x1 <- ts(data1,start = c(1971,3),frequency = 4)
plot(x1)#时序图
acf(x1)#自相关图
install.packages("aTSA")
library(aTSA)
adf.test(x1)#单位根检验for(i in 1:2)print(Box.test(x1,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x1)#偏自相关图
结果分析:
- 时序图:
该序列始终在常数50附近波动,且波动范围有界。无明显的趋势性或周期性。该序列是平稳序列。

自相关图:
显示除了lag=0.75和lag=2的自相关系数在2倍标准差范围之外,其他阶数的自相关系数都在2倍标准差范围内波动。可以判断该序列具有短期相关性,进一步确定序列平稳。

单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1-2阶滞后模型和既有漂移项又有趋势项的1-2阶滞后模型的P值小于0.05)。
adf.test(x1)
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -2.719 0.010
[2,] 1 -1.531 0.128
[3,] 2 -0.928 0.345
[4,] 3 -0.698 0.428
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -10.12 0.010
[2,] 1 -6.41 0.010
[3,] 2 -3.56 0.010
[4,] 3 -2.32 0.207
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -10.48 0.0100
[2,] 1 -6.88 0.0100
[3,] 2 -3.92 0.0172
[4,] 3 -2.57 0.3362
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x1
X-squared = 17.858, df = 6, p-value = 0.006597
Box-Ljung test
data: x1
X-squared = 17.858, df = 6, p-value = 0.006597
3.偏自相关图:
除了lag=0.75,lag=1,lag=1.75偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢。

练习2、根据某城市过去四年每个月人口净流入数量(行数据)(题目2数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
Data2 <- scan("F:/时间序列分析/实验5/习题数据/题目2数据.txt")
x2 <- ts(data2,start = c(2018,1),frequency = 12)
plot(x2)#时序图
acf(x2)#自相关图library(aTSA)
adf.test(x2)#单位根检验for(i in 1:2)print(Box.test(x2,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x2)#偏自相关图
结果分析:
- 时序图:
该序列始终在常数4附近波动,且波动范围有界。无明显的趋势性或周期性。该序列是平稳序列。

自相关图:
显示除了lag=1/12的自相关系数在2倍标准差范围之外,其他阶数的自相关系数都在2倍标准差范围内波动。可以判断该序列具有短期相关性,进一步确定序列平稳。

单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1-2阶滞后模型和既有漂移项又有趋势项的1-3阶滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -1.121 0.274
[2,] 1 -0.960 0.331
[3,] 2 -0.731 0.413
[4,] 3 -0.986 0.322
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -4.03 0.0100
[2,] 1 -4.49 0.0100
[3,] 2 -3.11 0.0356
[4,] 3 -2.93 0.0503
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -4.54 0.0100
[2,] 1 -5.74 0.0100
[3,] 2 -4.33 0.0100
[4,] 3 -3.81 0.0255
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都大于α=0.05,则接受原假设,认为序列是白噪声序列。
Box-Ljung test
data: x2
X-squared = 11.938, df = 6, p-value = 0.06336
Box-Ljung test
data: x2
X-squared = 11.938, df = 6, p-value = 0.06336
3.偏自相关图:
除了1/12阶偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢,序列平稳。
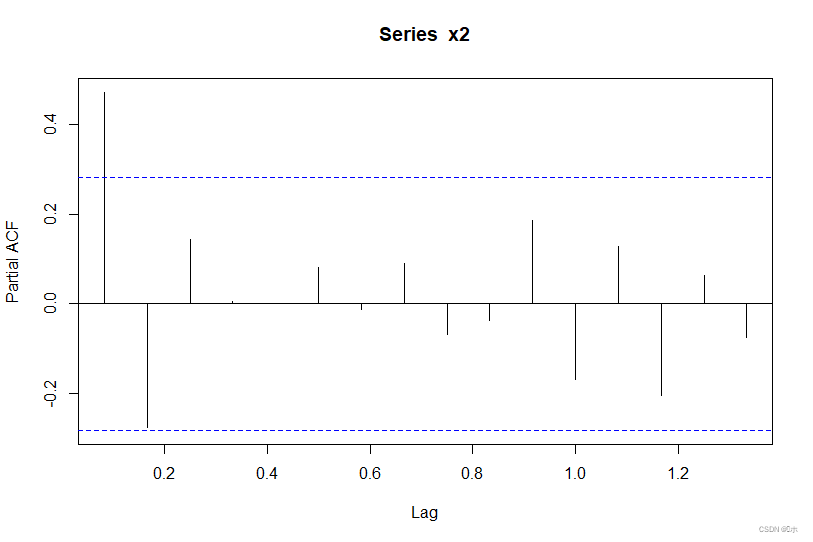
练习3、根据1975-1980年夏威夷岛莫那罗亚火山每月释放的CO2数据(题目3数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
data3 <- scan("F:/时间序列分析/实验5/习题数据/题目3数据.txt")
x3 <- ts(data3,start = c(1975,1),frequency = 12)
plot(x3)#时序图
acf(x3)#自相关图library(aTSA)
adf.test(x3)#单位根检验for(i in 1:2)print(Box.test(x3,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x3)
结果分析:
- 时序图:
该序列呈现出逐年的上升趋势且存在明显的周期性。该序列不是平稳序列。

自相关图:
显示大部分的自相关系数在2倍标准差范围之外,可认为该自相关数很大,显著非零。可以判断该序列是非序列平稳。
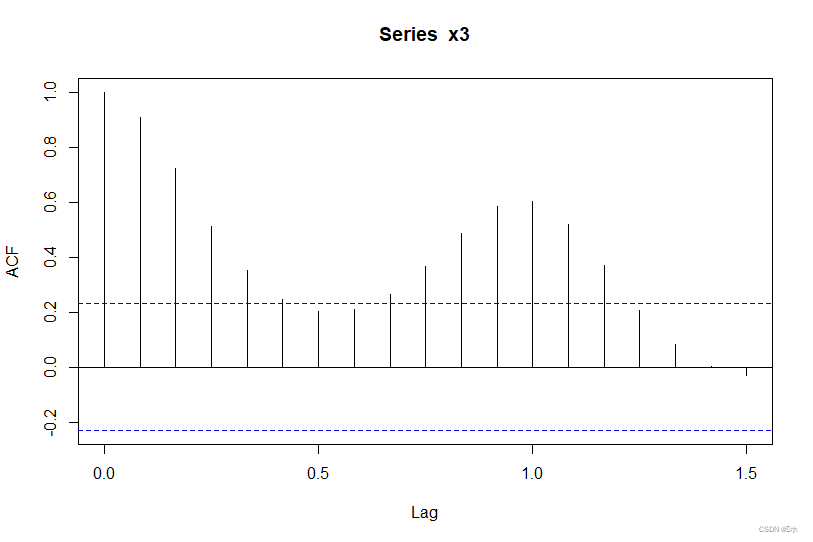
单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1阶滞后模型和既有漂移项又有趋势项的1-3阶滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 0.770 0.861
[2,] 1 0.277 0.720
[3,] 2 0.417 0.760
[4,] 3 0.448 0.769
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -1.63 0.472
[2,] 1 -4.16 0.010
[3,] 2 -2.43 0.164
[4,] 3 -1.64 0.465
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -2.49 0.368
[2,] 1 -8.69 0.010
[3,] 2 -6.03 0.010
[4,] 3 -5.25 0.010
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则接受原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x3
X-squared = 139.5, df = 6, p-value < 2.2e-16
Box-Ljung test
data: x3
X-squared = 139.5, df = 6, p-value < 2.2e-16
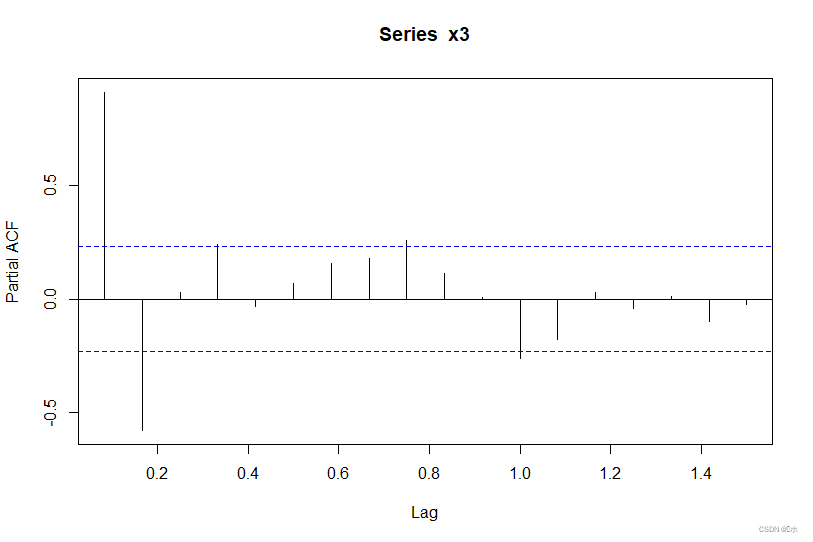
3.偏自相关图:
除了延迟1阶的偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢,这是一个典型的相关系数1阶结尾特征。
需要本练习原始数据请自行跳转下载:
博文:‘平稳性检验和ARMA模型的识别与定阶’训练数据资源-CSDN文库
相关文章:

时间序列分析 # 平稳性检验和ARMA模型的识别与定阶 #R语言
掌握单位根检验的原理并能解读结果;掌握利用序列的自相关图和偏自相关图识别模型并进行初步定阶。 原始数据在文末!!! 练习1、根据某1971年9月-1993年6月澳大利亚季度常住人口变动(单位:千人)的…...

算法-日期问题
算法-日期问题 1.判断是否闰年 int is_leap(int y) {if((y%4000)||(y%40&&y%100!0)){return 1;}return 0; }2.每个月的天数 const int months[]{0,31,28,31,30,31,30,31,31,30,31,30,31};3.计算当前年当前月的天数 int get_month_days(int year,int month) {int re…...
《由浅入深学习SAP财务》:第2章 总账模块 - 2.6 定期处理 - 2.6.5 年末操作:维护新财政年度会计凭证编号范围
2.6.5 年末操作:维护新财政年度会计凭证编号范围 财务系统的维护者要在每年年末预先设置好下一年度的会计凭证编号范围(number range),以便下一年度会计凭证能够顺利生成。这一操作一定要在下一年度1月1日以前预先完成。 …...

2024年第十七届“认证杯”数学中国数学建模网络挑战赛A题思路
A题 保暖纤维的保暖能力 冬装最重要的作用是保暖,也就是阻挡温暖的人体与寒冷环境之间的热量传递。人们在不同款式的棉衣中会填充保暖材料,从古已有之的棉花,羽绒到近年来各种各样的人造纤维。不同的保暖纤维具有不同的保暖性能,比如人们以往的经验表明,高品质的羽绒具有…...
Linux 添加启动服务--Service
1,服务配置service文件 Service 服务的实际作用是开启后自动启动服务,运行一些不须要登录的程序,任务。 实例1、上电自动连接WIFI热点 1.1 新建.service文件 /etc/systemd/system/wificonnect.service [Unit] DescriptionService [wifico…...
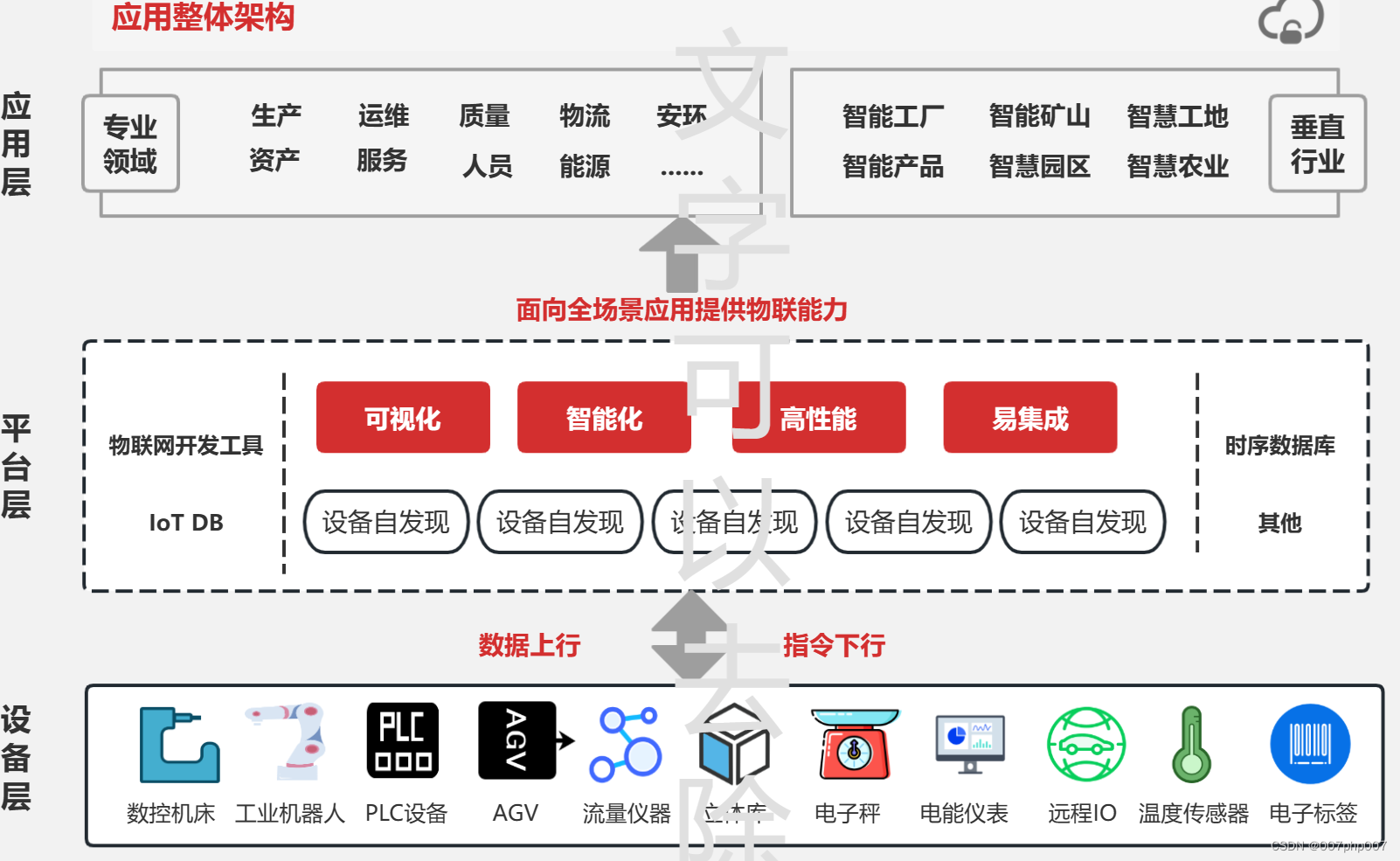
构建智能连接的未来:物联网平台系统架构解析
随着科技的不断进步和互联网的普及,物联网(Internet of Things, IoT)已成为连接世界的新方式。物联网平台作为实现物联网应用的核心基础设施,其系统架构的设计和实施至关重要。本文将深入探讨物联网平台系统架构的关键要素和最佳实…...

element-ui的年份范围选择器,选择的年份需等于或小于当前年份,选择的年份范围必须在三年之内
写在前面 日期限制处理(禁用),下面我以我这边的需求为例, 选择的年份需等于或小于当前年份 选择的年份范围必须在三年之内 1.限制起始日期小于截止日期 1)根据用户选中的开始日期,置灰不可选的日期范围&…...

2024年蓝桥杯40天打卡总结
2024蓝桥杯40天打卡总结 真题题解其它预估考点重点复习考点时间复杂度前缀和二分的两个模板字符串相关 String和StringBuilderArrayList HashSet HashMap相关蓝桥杯Java常用算法大数类BigInteger的存储与运算日期相关考点及函数质数最小公倍数和最大公约数排序库的使用栈Math类…...

STL函数对象
1,函数对象 1.1 函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象函数对象使用重载的()时,行为类似函数调用,也称为仿函数 本质: 函数对象(仿函数&…...

DedeCMS 未授权远程命令执行漏洞分析
dedecms介绍 DedeCMS是国内专业的PHP网站内容管理系统-织梦内容管理系统,采用XML名字空间风格核心模板:模板全部使用文件形式保存,对用户设计模板、网站升级转移均提供很大的便利,健壮的模板标签为站长DIY自己的网站提供了强有力…...

学习 Rust 的第二天:Cargo包管理器的使用
今天,我们来探讨一下 Cargo,这个强大而方便的 Rust 构建系统和包管理器。 Cargo 是一个稳健而高效的 Rust 构建系统和包管理器,旨在帮助管理项目依赖关系,并确保在不同环境下进行一致的构建。 使用 cargo 创建新程序:…...

【爬虫+数据清洗+可视化分析】Python文本分析《狂飙》电视剧的哔哩哔哩评论
一、背景介绍 把《狂飙》换成其他影视剧,套用代码即可得分析结论! 2023《狂飙》热播剧引发全民追剧,不仅全员演技在线,且符合主旋律,创下多个收视记录! 基于此热门事件,我用python抓取了B站上千…...

使用vite从头搭建一个vue3项目(二)创建目录文件夹以及添加vue-router
目录 一、创建 vue3 项目 vite-vue3-project-js二、创建项目目录三、创建Home、About组件以及 vue-router 配置路由四、修改完成后页面 一、创建 vue3 项目 vite-vue3-project-js 使用 vite 创建一个极简 vue3 项目请参考此文章:使用Vite创建一个vue3项目 下面是我…...
)
循环控制语句的实际应用(3)
3194:【例32.3】 数位积 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 5116 通过数: 1971 【题目描述】 給出一个非负整数n,请求出n中各个数位上的数字之积。 【输入】 一开始有一个整数 T(1≤T≤100),表示共有几组测试数据。接下来有T个…...

突破像素限制,尽显照片细腻之美——Topaz Gigapixel AI for Mac/Win
在这个数字化的时代,我们都热爱用照片记录生活中的美好瞬间。然而,有时候我们会发现,由于各种原因,照片的像素可能无法满足我们的需求。这时候,Topaz Gigapixel AI for Mac/Win 这款强大的照片放大工具应运而生。 Top…...

CSS特效---HTML+CSS实现3D旋转卡片
1、演示 2、一切尽在代码中 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Document</title&…...

Rust跨平台编译
❝ 如果你感觉自己被困住了,焦虑并充满消极情绪,生命出现了停滞,那么治疗方法很简单:「做点什么」。 ❞ 大家好,我是「柒八九」。一个「专注于前端开发技术/Rust及AI应用知识分享」的Coder 前言 之前我们不是写了一篇R…...

php其他反序列化知识学习
简单总结一下最近学习的,php其他的一些反序列化知识 phar soap session 其他 __wakeup绕过gc绕过异常非公有属性,类名大小写不敏感正则匹配,十六进制绕过关键字检测原生类的利用 phar 基础知识 在 之前学习的反序列化利用中࿰…...
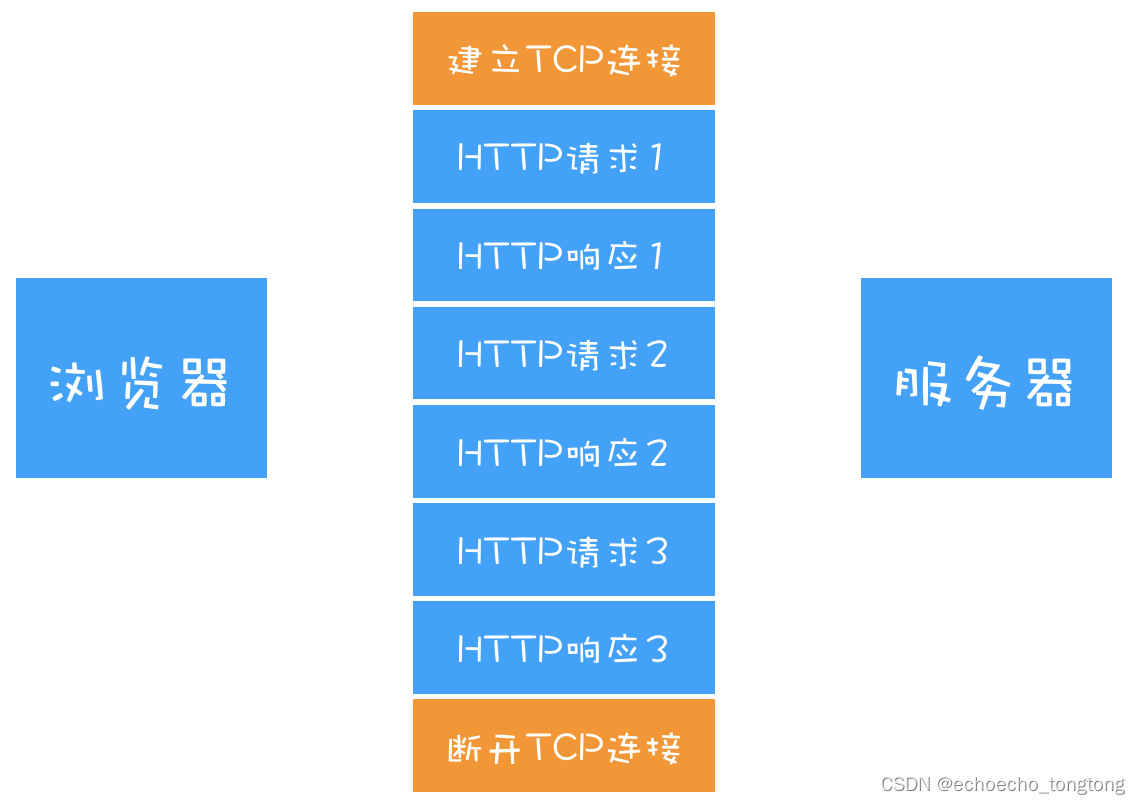
浏览器工作原理与实践--HTTP/1:HTTP性能优化
谈及浏览器中的网络,就避不开HTTP。我们知道HTTP是浏览器中最重要且使用最多的协议,是浏览器和服务器之间的通信语言,也是互联网的基石。而随着浏览器的发展,HTTP为了能适应新的形式也在持续进化,我认为学习HTTP的最佳…...

idea 使用springboot helper 创建springboot项目
Spring Boot Helper 是一个在 IntelliJ IDEA 中用于快速创建 Spring Boot 项目的插件。通过这个插件,开发者可以简化 Spring Boot 项目的创建过程,并快速生成所需的依赖和配置文件。以下是使用 Spring Boot Helper 插件创建 Spring Boot 项目的详细步骤&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
