LeetCode-72. 编辑距离【字符串 动态规划】
LeetCode-72. 编辑距离【字符串 动态规划】
- 题目描述:
- 解题思路一:动规五部曲
- 解题思路二:动态规划【版本二】
- 解题思路三:0
题目描述:
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
此题的解题思路与LeetCode-1143. 最长公共子序列【字符串 动态规划】非常一致!
解题思路一:动规五部曲
- 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
为什么这么定义我在 718. 最长重复子数组 (opens new window)中做了详细的讲解。
其实用i来表示也可以! 用i-1就是为了方便后面dp数组初始化的。
- 确定递推公式
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换
也就是如上4种情况。
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
此时可能有同学有点不明白,为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
在下面的讲解中,如果哪里看不懂,就回想一下dp[i][j]的定义,就明白了。
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了,怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = “ad” ,word2 = “a”,word1删除元素’d’ 和 word2添加一个元素’d’,变成word1=“a”, word2=“ad”, 最终的操作数是一样! dp数组如下图所示意的:
a a d+-----+-----+ +-----+-----+-----+| 0 | 1 | | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
递归公式代码如下:
if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];
}
else {dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
- dp数组如何初始化
再回顾一下dp[i][j]的定义:
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
- 确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]
dp[i][j] = dp[i - 1][j - 1] + 1
dp[i][j] = dp[i][j - 1] + 1
dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:

所以在dp矩阵中一定是从左到右从上到下去遍历。
- 举例推导dp数组
以示例1为例,输入:word1 = “horse”, word2 = "ros"为例,dp矩阵状态图如下:
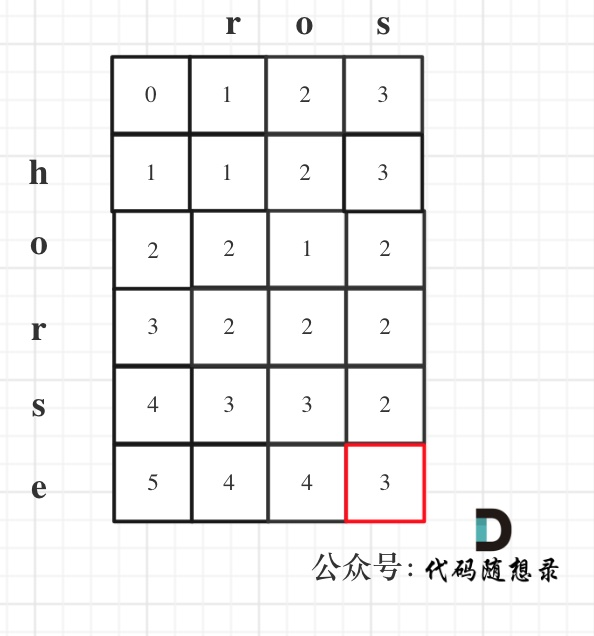
class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1return dp[-1][-1]
时间复杂度:O(nm)
空间复杂度:O(nm)
解题思路二:动态规划【版本二】
class Solution:def minDistance(self, word1: str, word2: str) -> int:m, n = len(word1), len(word2)dp = [[0] * (n+1) for _ in range(m+1)]for i in range(m+1):dp[i][0] = ifor j in range(n+1):dp[0][j] = jfor i in range(1, m+1):for j in range(1, n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1return dp[-1][-1]
时间复杂度:O(nm)
空间复杂度:O(nm)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)
相关文章:

LeetCode-72. 编辑距离【字符串 动态规划】
LeetCode-72. 编辑距离【字符串 动态规划】 题目描述:解题思路一:动规五部曲解题思路二:动态规划【版本二】解题思路三:0 题目描述: 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最…...

多张静图合成gif怎么做?一键极速合成gif
图片的格式有很多种,通常分为静态图片和动态图片。而动态图片基本上都是gif格式,想要把其他格式的静图变成gif格式动图的时候要怎么操作呢?通过使用gif动画图片(https://www.gif.cn/)制作网站,上传jpg、png…...
)
Es中bool 查询中的四个(must must_not should filter)
1.must :相当于and 2.must_not :相当于not 3.should:相当于or 4. filter:过滤 gte 大于 gt大于 lte小于等于 lt小于 使用示例: {“bool”:{“must”:{“match”:{“title”:”how to make millons “}},“must_not”:{“match”:{“tag”:”spam“}},“should”:[{…...
Docker容器嵌入式开发:Docker Ubuntu18.04配置mysql数据库
在 Ubuntu 18.04 操作系统中安装 MySQL 数据库的过程。下面是安装过程的详细描述: 首先,使用以下命令安装 MySQL 服务器: sudo apt install mysql-server系统会提示是否继续安装,按下 Y 键确认。 安装过程中,系统会…...

C++类和对象中上篇
1.类的6个默认成员函数 如果一个类中什么成员都没有,那就简称他为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,…...
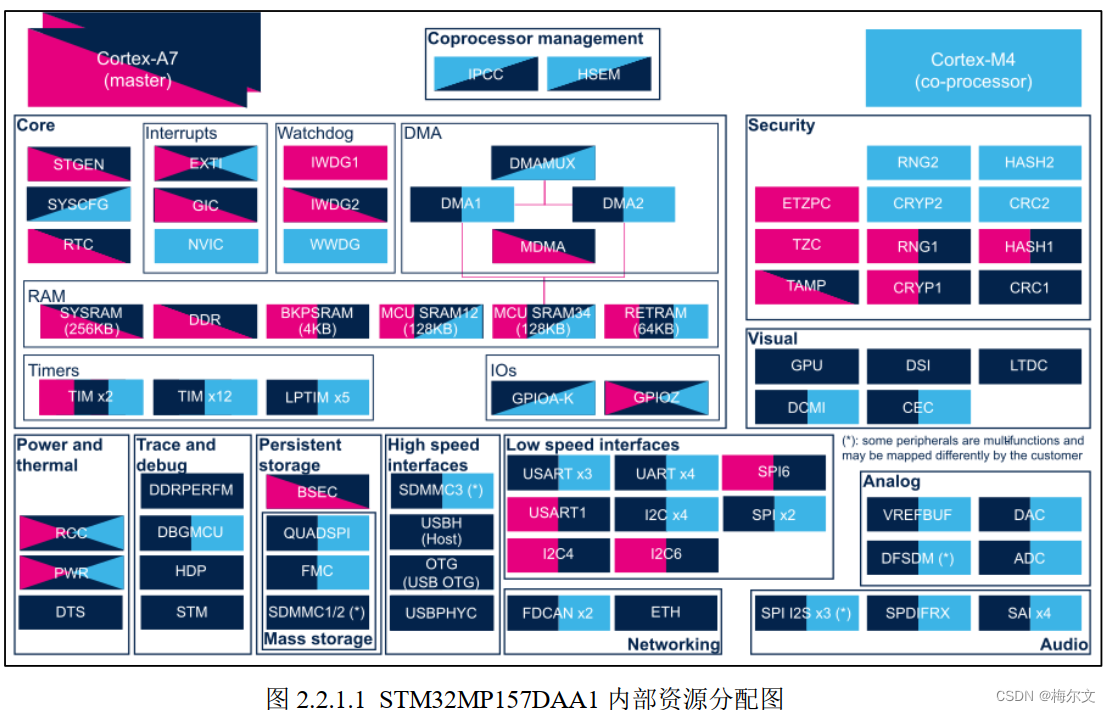
基于linux进一步理解核间通讯
芯片架构分为同构和异构: 如下图TC397: 如下图TDA4: 如下图STM32MP157: 非对称多处理结构(AMP): AMP 结构是指每个内核运行自己的 OS 或同一 OS 的独立实例&#...
应用实战|从头开始开发记账本2:基于模板快速开始
上期视频我们创建好了BaaS服务的后端应用。从这期视频开始,我们将从头开发一个互联网记账本应用。本期视频我们介绍一下如何使用模板快速开启我们的应用开发之旅。 应用实战|从头开始开发记账本2:基于模板快速开始 相关代码 本期视频我们介绍…...
)
学习前端第二十天(条件分支:if 和 ‘?‘;逻辑运算符)
一、条件分支 if (…) 语句会计算圆括号内的表达式,并将计算结果转换为布尔型。 if(...) 语句计算括号里的条件表达式,如果计算结果是 true,就会执行对应的代码块{ }。 if 语句有时会包含一个可选的 “else” 块。如果判断条件不成立&…...

C++11的更新介绍(lamada、包装器)
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 总有光环在陨落,总有新星在闪烁 lambda表达式 C98中的一个…...

Golang 实现一个简单的 RPC 服务
分享一个简单的 rpc 服务框架 一、服务端实现 package mainimport ("log""net""net/rpc" )const HelloServiceName "main.HelloService"type HelloServiceInterface interface {Hello(request string, replay *string) error }func…...
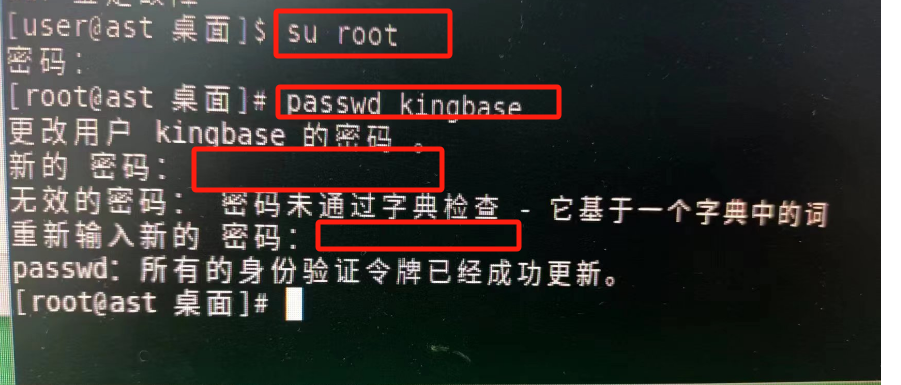
Linux系统(centos,redhat,龙芯,麒麟等)忘记密码,怎么设置新的密码
Linux系统(centos,redhat,龙芯,麒麟等)忘记密码,怎么设置新的密码 今天在操作服务器时,DBA忘记了人大金仓数据库的kingbase密码,他的密码试了好多遍,都不行。最后只能给重置密码了 解决办法&a…...

SpringBoot的启动原理
运行Main方法: 应用程序启动始于Main方法的执行。在Main方法中,创建了一个SpringApplication实例,用于引导应用程序的启动。同时,SpringApplication会根据spring.factories文件加载并注册监听器、ApplicationContextInitializer等…...
git查看单独某一个文件的历史修改记录
git查看单独某一个文件的历史修改记录 git log -p 文件具体路径 注意,Windows下默认文件路径分隔符是 \,在git bash 里面需要改成 /。 git基于change代码修改与提交_git change-CSDN博客文章浏览阅读361次。git cherry-pick:复制多个提交comm…...

一键开启Scrum回顾会议的精彩时刻
其实回顾会议作为一个检视、反馈、改进环节,不仅在传统的瀑布管理模式中,还是在Scrum一类的敏捷管理流程中,都是非常重要的活动。一些团队认为它无法产生直接的价值,所以有意忽略了这个会议;一些团队在越来越多的回顾中…...
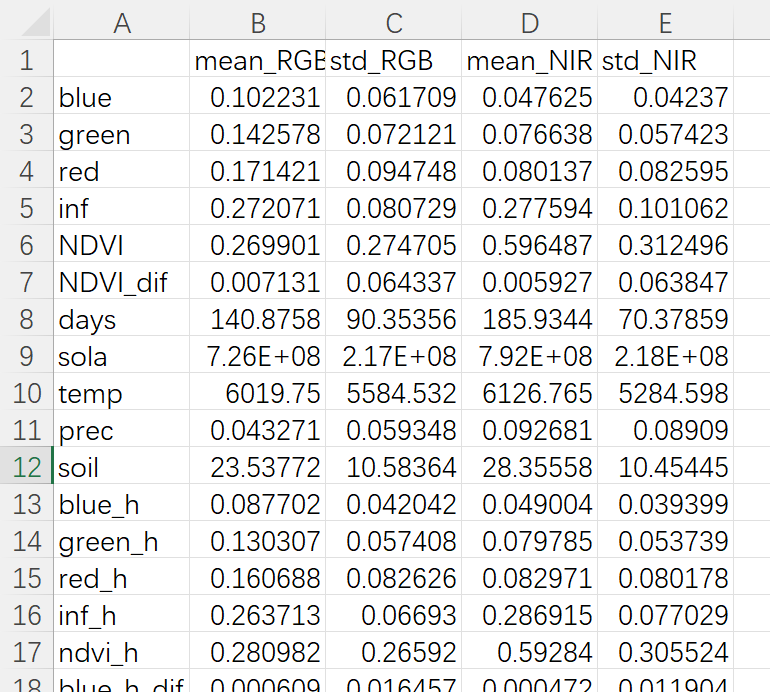
Python计算多个表格中多列数据的平均值与标准差并导出为新的Excel文件
本文介绍基于Python语言,对一个或多个表格文件中多列数据分别计算平均值与标准差,随后将多列数据对应的这2个数据结果导出为新的表格文件的方法。 首先,来看一下本文的需求。现有2个.csv格式的表格文件,其每1列表示1个变量&#x…...
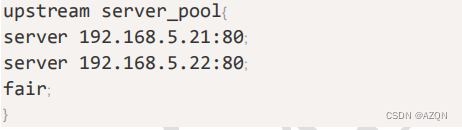
nginx支持的多种负载均衡策略
目录 1.轮询(默认) 2. ip_hash 3. 加权轮询(weight) 4. fair(第三方) 5. 最少连接(least_conn) 1.轮询(默认) 将请求依次分配给每个服务器,确…...

FNP preptool has not been run on this executable
pycharm导入arcgis pro的python运行程序后提示 我也看了很多解决方法,也重新安装过一遍,终于看到一个说法是你的arcgis pro是学习版所以才会有这个提示,不会影响输入 测试代码 import arcpy print(arcpy.GetInstallInfo()[Version])输出结果…...

算法-反转单向链表
需求 思路 链表必有节点,节点两要素:当前元素值,下一个节点地址 import java.util.Scanner;// 定义一个单向链表 public class MyLinkedList<E> {int size 0;// 顶一个私有的内部类,表示链表的节点public class Node {E da…...

Ps 滤镜:方框模糊
Ps菜单:滤镜/模糊/方框模糊 Filter/Blur/Box Blur 方框模糊 Box Blur滤镜通过计算图像中每个像素及其周围像素的平均颜色值来实现模糊效果。适合于需要突出主题、减少背景(尤其是颜色变化)干扰的场景。 “方框模糊”滤镜按照设定的半径值&…...

MTK Android13 霸屏实现
一、背景 在台式POS场景下,经常有应用会需要获取霸屏的权限,隐藏状态栏或者导航栏,且不能被划出,其实系统已经系统了隐藏状态栏也导航栏的接口,但是无法做到禁止滑出。 View decorView ((Activity) context).getWin…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
