蓝桥杯(填空题)
十四届
B组 日期统计(暴力枚举)

数据
5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2
7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1
0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3审清题意:人家问的是这些数当中的子序列 有没有符合 2023mmdd 的 不是找能够多少个
答案:235
#include<iostream>
#include<cstring>
#include<map>
#include<set>
using namespace std;
int month[13]={0,1,2,3,4,5,6,7,8,9,10,11,12};
int day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int a[110];
int main()
{for(int i=1;i<=100;i++) cin>>a[i];int sum=0;for(int i=1;i<=12;i++){for(int j=1;j<=day[i];j++){int b[8]={2,0,2,3,i/10,i%10,j/10,j%10};int l=0;for(int i=1;i<=100;i++){if(b[l]==a[i]){l++;}if(l==8) break;}if(l==8) sum++;}}cout<<sum<<endl;return 0;
}第十三届
A组 灭鼠先锋(博弈)

答案:LLLV

#include<iostream>
#include<cstring>
#include<queue>
#include<map>
using namespace std;
map<string,bool>sg;
// 判断是否仅存在一个空格(O)
// 扫描字符串并对O的数量计数
bool check(string str)
{int cnt=0;for(int i=0;i<str.size();i++){if(str[i]=='O') cnt++;}if(cnt==1) return true;return false;
}
/*
* 后手必胜/必败
*/
bool dfs(string str)
{if(sg.count(str)) return sg[str];// 记忆化// 如果只有一个空位,也就是说后手必败if(check(str)) return sg[str]=false;/** 模拟放一个的情况*/for(int i=0;i<str.size();i++){if(str[i]=='O'){string s=str;s[i]='X';// 可达必败均为必胜// 意思是存在当前选手下了某一步棋之后,后面的选手不管怎么下都必败if(!dfs(s)) return sg[str]=true;}}/** 模拟放两个的情况*/for(int i=0;i<str.size()-1;i++){ // i!=3是什么意思?因为这里是把两行排成一行了,不能第一行最后一个+第二行第一个算作连续两个if(str[i]=='O'&&str[i+1]=='O'&&i!=3){string s=str;s[i]='X';s[i+1]='X';// 可达必败均为必胜if(!dfs(s)) return sg[str]=true;}}// 只达必胜均为必败// 排除了所有可能到达必败态的情况,接下来不管自己或者下一步对方怎么下对方都必胜,自己必败return sg[str]=false;
}
int main()
{// 表示棋盘的四种状态string str[4]={"XOOOOOOO","XXOOOOOO","OXOOOOOO","OXXOOOOO"};for(int i=0;i<4;i++){sg.clear();if(dfs(str[i])) cout<<"L";// 后手必胜else cout<<"V"; }return 0;
} 
研究生组 小蓝与药匙(错排)
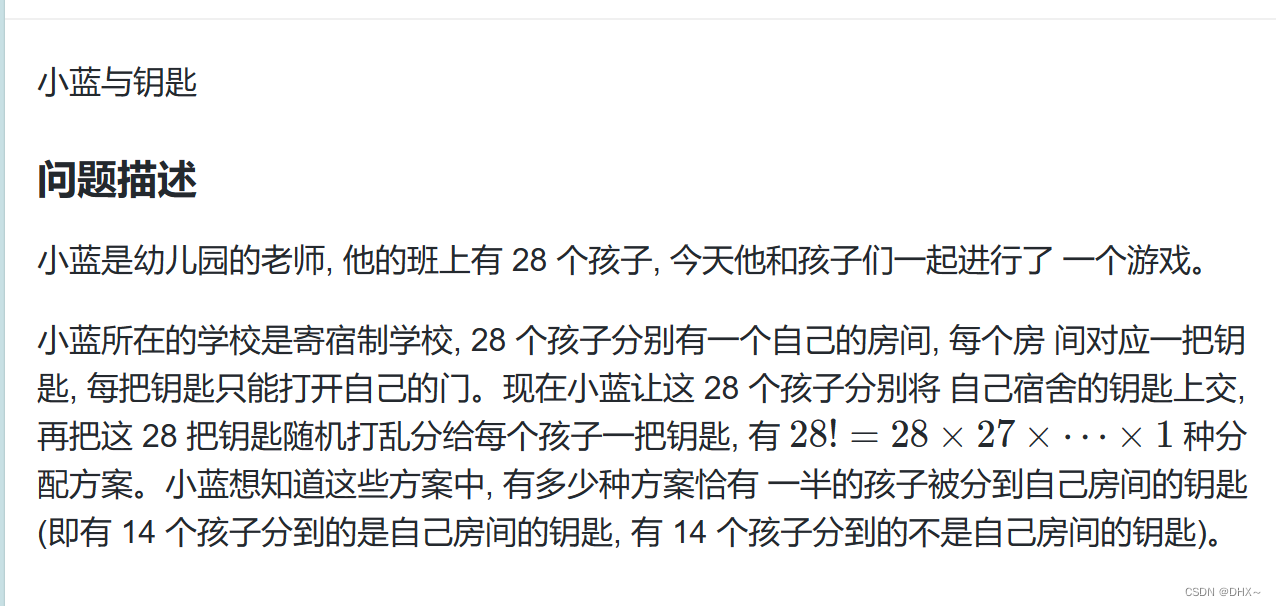
思路:从28把钥匙中选14(14钥匙一 一对应对应对的门) 然后让剩下的14把钥匙错排
错排公式
An=(n-1)*(An-1+An-2)
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int N=30;
int f[N];
signed main()
{int num=1,num1=1;for(int i=15;i<=28;i++) num*=i;for(int i=1;i<=14;i++) num1*=i;num/=num1;f[1]=0;f[2]=1;for(int i=3;i<=14;i++){f[i]=(i-1)*(f[i-1]+f[i-2]);}cout<<f[14]*num<<endl;return 0;
}
相关文章:

蓝桥杯(填空题)
十四届 B组 日期统计(暴力枚举) 数据 5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1 0 0 9 4 8 0 9 1 2 8 5 0 2 5 3…...

vim快捷指令
Vim是一款强大的文本编辑器,它提供了许多快捷指令来提高编辑效率。以下是一些常用的Vim快捷指令: 移动光标: h 向左移动一个字符j 向下移动一行k 向上移动一行l 向右移动一个字符w 跳到下一个单词的开头b 跳到前一个单词的开头e 跳到当前单词…...

LINUX 下IPTABLES配置详解
-t<表>:指定要操纵的表; -A:向规则链中添加条目; -D:从规则链中删除条目; -i:向规则链中插入条目; -R:替换规则链中的条目; -L:显示规则链中…...

CentOS 网卡ifcfg-eth0 ping不通外网(www.baidu.com)
1、如果确认好就直接激活网卡! ifup eth0 2、慢慢找: cd /etc/sysconfig/network-scripts/ ls 找到你的网卡是啥,这里网卡是 ifcfg-eth0 执行1就好了!...
【C++】类和对象②(类的默认成员函数:构造函数 | 析构函数)
🔥个人主页:Forcible Bug Maker 🔥专栏:C 目录 前言 类的6个默认成员函数 构造函数 概念 构造函数的特性及用法 析构函数 概念 析构函数的特性及用法 结语 前言 本篇主要内容:类的6个默认成员函数中的构造函…...
)
【ZZULIOJ】1063: 最大公约与最小公倍(Java)
目录 题目描述 输入 输出 样例输入 Copy 样例输出 Copy 提示 code 题目描述 输入两个正整数,输出其最大公约数和最小公倍数。 输入 输入两个正整数n和m(n,m<1000000)。输入保证最终结果在int范围内。 输出 输出两个整数,用空格…...

遍历列举俄罗斯方块的所有形状
以前玩俄罗斯方块的时候,就想过一个问题,为什么俄罗斯方块就这7种形状,还有没有别的形状?自己也在纸上画过,比划来比划去,确实就这几种形状。 继续思考一下,那假如是3个块组合的形状࿰…...
将Visio绘图导出PDF文件,使其自适应大小,并去掉导入Latex的边框显示
问题描述 将Visio绘图导成pdf文件,首先在Visio绘图如下: 如果直接导出或者另存为pdf文件,则会发现pdf文件是整个页面大小,而不是图片大小。而且在导入latex等排版工具现实时,会显示边框。 问题解决 1.调整Visio中的页…...
android支付宝接入流程
接入前准备 接入APP支付能力前,开发者需要完成以下前置步骤。 本文档展示了如何从零开始,使用支付宝开放平台服务端 SDK 快速接入App支付产品,完成与支付宝对接的部分。 第一步:创建应用并获取APPID 要在您的应用中接入支付宝…...

Mac 下 Python+Selenium 自动上传西瓜视频
背景 研究下 PythonSelenium 自动化测试框架,简单实现 Mac 下自动化批量上传视频西瓜视频并发布,分享给需要的同学(未做过多的异常处理)。 脚本实现 首先通过手工手机号登录,保存西瓜视频网站的 cookie 文件 之后加载…...
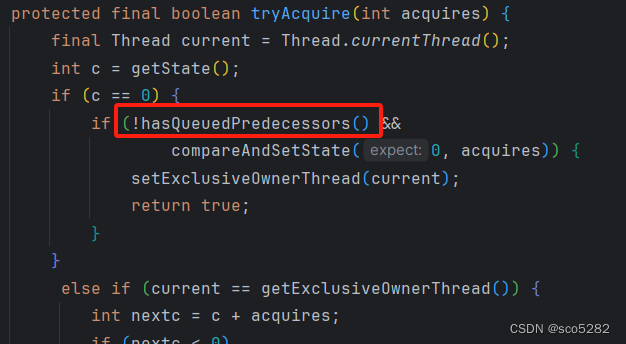
六:ReentrantLock —— 可重入锁
目录 1、ReentrantLock 入门2、ReentrantLock 源码解析2.1、构造方法:默认为非公平锁2.2、三大内部类2.2、lock():加锁【不可中断锁】2.2.1、acquire() 方法 —— AQS【模板方法】2.2.2.1 tryAcquire() 方法 —— AQS,由子类去实现2.2.2.2. a…...
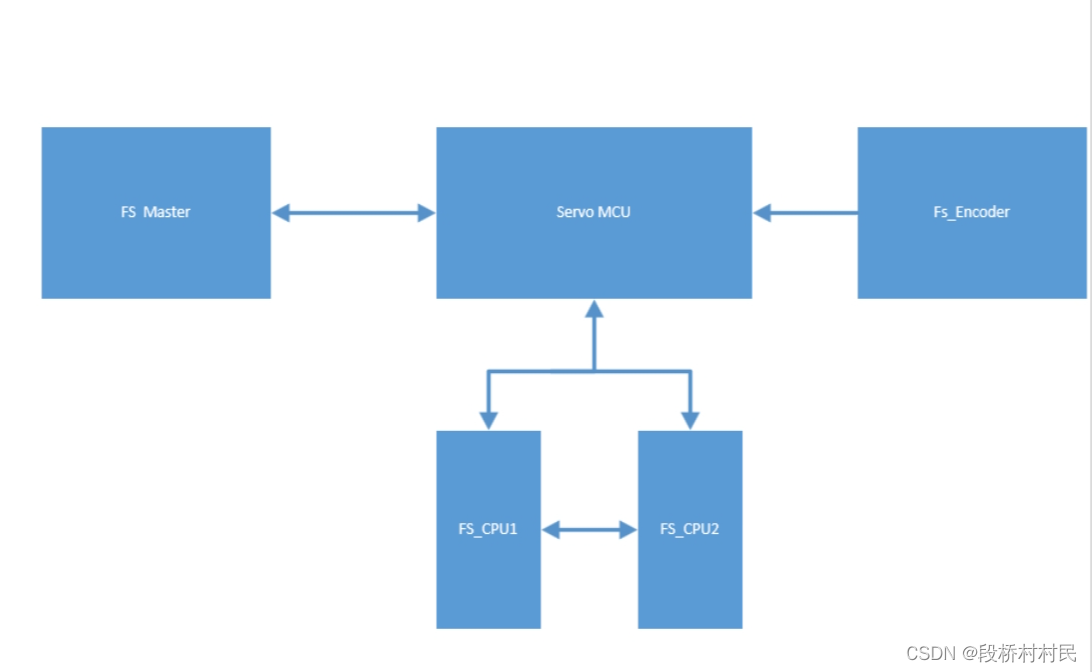
一种驱动器的功能安全架构介绍
下图提供了驱动器实现安全功能的架构 具有如下特点: 1.通用基于总线或者非总线的架构。可以实现ethercat的FSOE,profinet的profisafe,或者伺服本体安全DIO现实安全功能。 2.基于1oo2D架构,安全等级可以达到sil3。 3.高可用性。单…...

紫光展锐T610平台_4G安卓核心板方案定制开发
紫光展锐T610核心板配备Android 11操作系统,采用12nm制程工艺。该处理器CPU由2颗基于Cortex-A75架构的大核心和6颗基于Cortex-A55架构的小核心组成,最高主频为1.8GHz。GPU采用的是614.4MHz的Mali G52,可以流畅播放2400*1080分辨率视频&#x…...
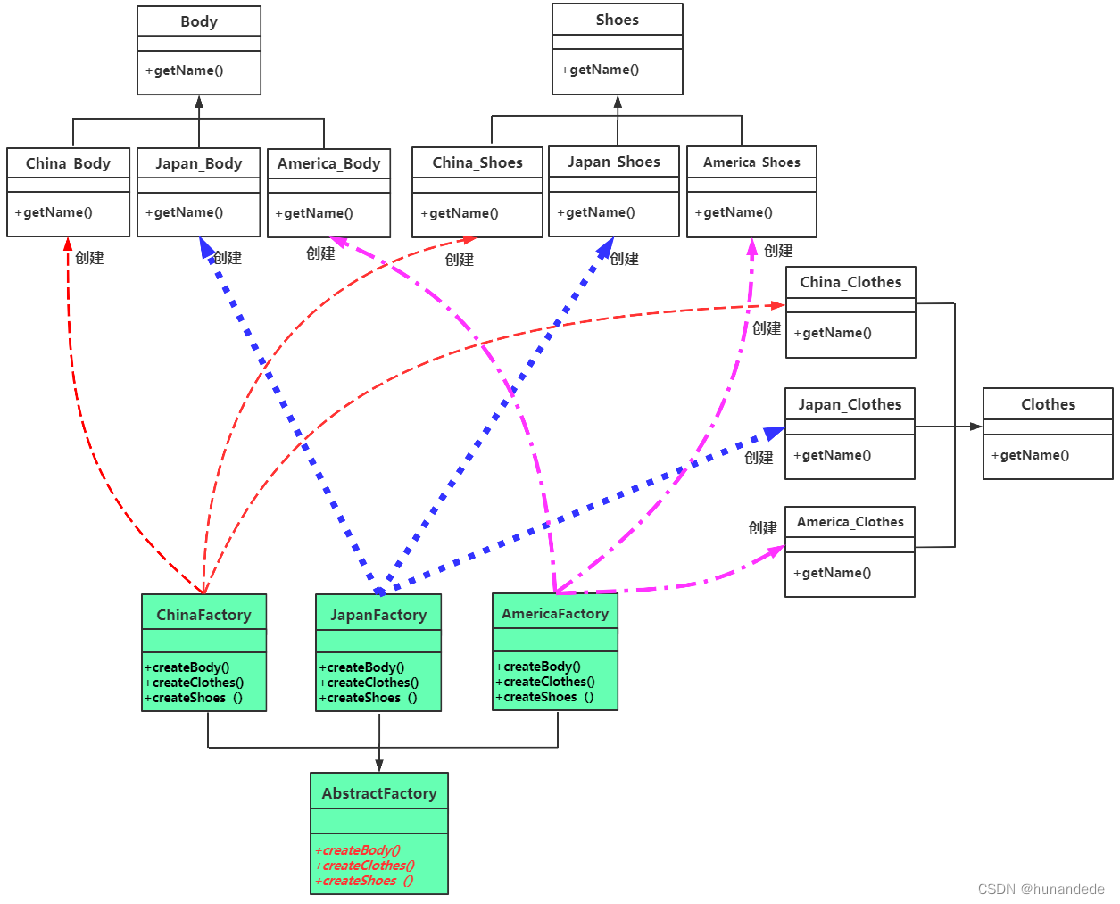
C++11 设计模式4. 抽象工厂(Abstract Factory)模式
问题的提出 从前面我们已经使用了工厂方法模式 解决了一些问题。 现在 策划又提出了新的需求:对于各个怪物,在不同的场景下,怪物的面板数值会发生变化, //怪物分类:亡灵类,元素类,机械类 …...

第8周 Python面向对象编程刷题
单击题目,直接跳转到页面刷题,一周后公布答案。加入QQ群701657573,随时答疑交流。 218:类对象属性219:坐标对象相加220:计算周长221:学生分数总和222:车辆类中创建引擎类对象223&am…...
【学习心得】神经网络知识中的符号解释②
我在上篇文章中初步介绍了一些神经网络中的符号,只有统一符号及其对应的含义才能使我自己在后续的深度学习中有着一脉相承的体系。如果对我之前的文章感兴趣可以点击链接看看哦: 【学习心得】神经网络知识中的符号解释①http://t.csdnimg.cn/f6PeJ 一、…...

Igh related:Small Bug And Notes Record.
Write at the top My computer got some silly problem with the typing software that my Chinese IM does’t work again. So I’ll try to record the things happened in English. If any error,DM me plz. BUGs BUG1 Undefined symbol Identifier “CLOCK_MONOTONIC”…...
)
【QT入门】Qt自定义控件与样式设计之qss介绍(Qt style sheet)
往期回顾: 【QT入门】 无边框窗口设计之实现圆角窗口-CSDN博客【QT入门】 无边框窗口设计综合运用之自定义标题栏带圆角阴影的窗口-CSDN博客 【QT入门】 无边框窗口设计之综合运用,实现WPS的tab页面-CSDN博客 【QT入门】Qt自定义控件与样式设计之qss介绍…...
-第49题:字母异位词分组)
[ LeetCode ] 题刷刷(Python)-第49题:字母异位词分组
题目描述 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词是由重新排列源单词的所有字母得到的一个新单词。 即将含有相同字符但排列顺序不同的字符串放入同一个组中。 示例 示例 1: 输入: strs ["eat", &qu…...

冒泡排序算法实现步骤
算法实现的过程: 1. 定义问题: - 算法是用来解决某一特定计算问题的方法步骤。例如,对于排序问题,我们需要一个算法对一组无序的整数进行排序。 2. 设计算法: - 冒泡排序是一种基础的排序算法。它的设计思路是…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
