Python图像处理:频域滤波降噪和图像增强
图像处理已经成为我们日常生活中不可或缺的一部分,涉及到社交媒体和医学成像等各个领域。通过数码相机或卫星照片和医学扫描等其他来源获得的图像可能需要预处理以消除或增强噪声。频域滤波是一种可行的解决方案,它可以在增强图像锐化的同时消除噪声。
快速傅里叶变换(FFT)是一种将图像从空间域变换到频率域的数学技术,是图像处理中进行频率变换的关键工具。通过利用图像的频域表示,我们可以根据图像的频率内容有效地分析图像,从而简化滤波程序的应用以消除噪声。本文将讨论图像从FFT到逆FFT的频率变换所涉及的各个阶段,并结合FFT位移和逆FFT位移的使用。
本文使用了三个Python库,即openCV、Numpy和Matplotlib。
importcv2importnumpyasnpfrommatplotlibimportpyplotaspltimg=cv2.imread('sample.png',0) # Using 0 to read image in grayscale modeplt.imshow(img, cmap='gray') #cmap is used to specify imshow that the image is in greyscaleplt.xticks([]), plt.yticks([]) # remove tick marksplt.show()

1、快速傅里叶变换(FFT)
快速傅里叶变换(FFT)是一种广泛应用的数学技术,它允许图像从空间域转换到频率域,是频率变换的基本组成部分。利用FFT分析,可以得到图像的周期性,并将其划分为不同的频率分量,生成图像频谱,显示每个图像各自频率成分的振幅和相位。
f=np.fft.fft2(img) #the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f mag=20*np.log(np.abs(f))plt.imshow(mag, cmap='gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.plt.title('Magnitude Spectrum') plt.xticks([]), plt.yticks([])plt.show()

上面代码使用np.abs()计算傅里叶变换f的幅度,np.log()转换为对数刻度,然后乘以20得到以分贝为单位的幅度。这样做是为了使幅度谱更容易可视化和解释。
2、FFT位移
为了使滤波算法应用于图像,利用FFT移位将图像的零频率分量被移动到频谱的中心
fshift = np.fft.fftshift(f)mag = 20*np.log(np.abs(fshift)) plt.imshow(mag, cmap = 'gray')plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])plt.show()

3、过滤
频率变换的的一个目的是使用各种滤波算法来降低噪声和提高图像质量。两种最常用的图像锐化滤波器是Ideal high-pass filter 和Gaussian high-pass filter。这些滤波器都是使用的通过快速傅里叶变换(FFT)方法获得的图像的频域表示。
Ideal high-pass filter(理想滤波器) 是一种无限长的、具有无限频带宽和理想通带和阻带响应的滤波器。其通带内所有频率的信号都被完全传递,而阻带内所有频率的信号则完全被抑制。
在频域上,理想滤波器的幅频响应为:
- 在通带内,幅频响应为 1
- 在阻带内,幅频响应为 0
在时域上,理想滤波器的冲激响应为:
- 在通带内,冲激响应为一个无限长的单位冲激函数序列
- 在阻带内,冲激响应为零
由于理想滤波器在频域上具有无限带宽,因此它无法在实际应用中实现。实际中使用的数字滤波器通常是基于理想滤波器的逼近,所以才被成为只是一个Ideal。
高斯高通滤波器(Gaussian high-pass filter)是一种在数字图像处理中常用的滤波器。它的作用是在图像中保留高频细节信息,并抑制低频信号。该滤波器基于高斯函数,具有光滑的频率响应,可以适应各种图像细节。
高斯高通滤波器的频率响应可以表示为:
H(u,v) = 1 - L(u,v)
其中,L(u,v)是一个低通滤波器,它可以用高斯函数表示。通过将低通滤波器的响应从1中减去,可以得到一个高通滤波器的响应。在实际中,通常使用不同的参数设置来调整高斯函数,以达到不同的滤波效果。
圆形掩膜(disk-shaped images)是用于定义在图像中进行傅里叶变换时要保留或抑制的频率分量。在这种情况下,理想滤波器通常是指理想的低通或高通滤波器,可以在频域上选择保留或抑制特定频率范围内的信号。将这个理想滤波器应用于图像的傅里叶变换后,再进行逆变换,可以得到经过滤波器处理后的图像。
具体的细节我们就不介绍了,直接来看代码:
下面函数是生成理想高通和低通滤波器的圆形掩膜
importmathdefdistance(point1,point2):returnmath.sqrt((point1[0]-point2[0])**2+ (point1[1]-point2[1])**2)defidealFilterLP(D0,imgShape):base=np.zeros(imgShape[:2])rows, cols=imgShape[:2]center= (rows/2,cols/2)forxinrange(cols):foryinrange(rows):ifdistance((y,x),center) <D0:base[y,x] =1returnbasedefidealFilterHP(D0,imgShape):base=np.ones(imgShape[:2])rows, cols=imgShape[:2]center= (rows/2,cols/2)forxinrange(cols):foryinrange(rows):ifdistance((y,x),center) <D0:base[y,x] =0returnbase
下面函数生成一个高斯高、低通滤波器与所需的圆形掩膜
importmathdefdistance(point1,point2):returnmath.sqrt((point1[0]-point2[0])**2+ (point1[1]-point2[1])**2)defgaussianLP(D0,imgShape):base=np.zeros(imgShape[:2])rows, cols=imgShape[:2]center= (rows/2,cols/2)forxinrange(cols):foryinrange(rows):base[y,x] =math.exp(((-distance((y,x),center)**2)/(2*(D0**2))))returnbasedefgaussianHP(D0,imgShape):base=np.zeros(imgShape[:2])rows, cols=imgShape[:2]center= (rows/2,cols/2)forxinrange(cols):foryinrange(rows):base[y,x] =1-math.exp(((-distance((y,x),center)**2)/(2*(D0**2))))returnbase
过滤示例
fig, ax=plt.subplots(2, 2) # create a 2x2 grid of subplotsfig.suptitle('Filters') # set the title for the entire figure# plot the first image in the top-left subplotim1=ax[0, 0].imshow(np.abs(idealFilterLP(50, img.shape)), cmap='gray')ax[0, 0].set_title('Low Pass Filter of Diameter 50 px')ax[0, 0].set_xticks([])ax[0, 0].set_yticks([])# plot the second image in the top-right subplotim2=ax[0, 1].imshow(np.abs(idealFilterHP(50, img.shape)), cmap='gray')ax[0, 1].set_title('High Pass Filter of Diameter 50 px')ax[0, 1].set_xticks([])ax[0, 1].set_yticks([])# plot the third image in the bottom-left subplotim3=ax[1, 0].imshow(np.abs(gaussianLP(50 ,img.shape)), cmap='gray')ax[1, 0].set_title('Gaussian Filter of Diameter 50 px')ax[1, 0].set_xticks([])ax[1, 0].set_yticks([])# plot the fourth image in the bottom-right subplotim4=ax[1, 1].imshow(np.abs(gaussianHP(50 ,img.shape)), cmap='gray')ax[1, 1].set_title('Gaussian Filter of Diameter 50 px')ax[1, 1].set_xticks([])ax[1, 1].set_yticks([])# adjust the spacing between subplotsfig.subplots_adjust(wspace=0.5, hspace=0.5)# save the figure to a filefig.savefig('filters.png', bbox_inches='tight')

相乘过滤器和移位的图像得到过滤图像
为了获得具有所需频率响应的最终滤波图像,关键是在频域中对移位后的图像与滤波器进行逐点乘法。
这个过程将两个图像元素的对应像素相乘。例如,当应用低通滤波器时,我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
4、乘法滤波器(Multiplying Filter)和平移后的图像(Shifted Image)
乘法滤波器是一种以像素值为权重的滤波器,它通过将滤波器的权重与图像的像素值相乘,来获得滤波后的像素值。具体地,假设乘法滤波器的权重为h(i,j),图像的像素值为f(m,n),那么滤波后的像素值g(x,y)可以表示为:
g(x,y) = ∑∑ f(m,n)h(x-m,y-n)
其中,∑∑表示对所有的(m,n)进行求和。
平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率,但它们的像素位置发生了变化。在滤波操作中,平移后的图像可以用于与滤波器进行卷积运算,以实现滤波操作。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
fig, ax=plt.subplots()im=ax.imshow(np.log(1+np.abs(fftshifted_image*idealFilterLP(50,img.shape))), cmap='gray')ax.set_title('Filtered Image in Frequency Domain')ax.set_xticks([])ax.set_yticks([])fig.savefig('filtered image in freq domain.png', bbox_inches='tight')

在可视化傅里叶频谱时,使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题,可以取决于具体的应用程序。
一般情况下会使用Np.log (1+np.abs(x)),因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的,并加上1以避免取零的对数。
而20*np.log(np.abs(x))将数据按20倍缩放,并对数据的绝对值取对数,这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。
这两种方法都有各自的优点和缺点,最终取决于具体的应用程序和个人偏好。
5、逆FFT位移
在频域滤波后,我们需要将图像移回原始位置,然后应用逆FFT。为了实现这一点,需要使用逆FFT移位,它反转了前面执行的移位过程。
fig, ax=plt.subplots()im=ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image*idealFilterLP(50,img.shape)))), cmap='gray')ax.set_title('Filtered Image inverse fft shifted')ax.set_xticks([])ax.set_yticks([])fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')

6、快速傅里叶逆变换(IFFT)
快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比,图像减少了噪声并提高了清晰度。
fig, ax=plt.subplots()im=ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image*idealFilterLP(50,img.shape))))), cmap='gray')ax.set_title('Final Filtered Image In Spatial Domain')ax.set_xticks([])ax.set_yticks([])fig.savefig('final filtered image.png', bbox_inches='tight')

总结
我们再把所有的操作串在一起显示,
函数绘制所有图像
defFreq_Trans(image, filter_used):img_in_freq_domain=np.fft.fft2(image)# Shift the zero-frequency component to the center of the frequency spectrumcentered=np.fft.fftshift(img_in_freq_domain)# Multiply the filter with the centered spectrumfiltered_image_in_freq_domain=centered*filter_used# Shift the zero-frequency component back to the top-left corner of the frequency spectruminverse_fftshift_on_filtered_image=np.fft.ifftshift(filtered_image_in_freq_domain)# Apply the inverse Fourier transform to obtain the final filtered imagefinal_filtered_image=np.fft.ifft2(inverse_fftshift_on_filtered_image)returnimg_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image
使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素,展示它们对增强图像清晰度的影响。
fig, axs=plt.subplots(12, 7, figsize=(30, 60))filters= [(f, d) forfin [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] fordin [50, 100, 150]]forrow, (filter_name, filter_diameter) inenumerate(filters):# Plot each filter output on a separate subplotresult=Freq_Trans(img, filter_name(filter_diameter, img.shape))forcol, title, img_arrayinzip(range(7), ["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])), np.log(1+np.abs(result[4])), np.abs(result[5])]):axs[row, col].imshow(img_array, cmap='gray')axs[row, col].set_title(title)plt.tight_layout()plt.savefig('all_processess.png', bbox_inches='tight')plt.show()

可以看到,当改变圆形掩膜的直径时,对图像清晰度的影响会有所不同。随着直径的增加,更多的频率被抑制,从而产生更平滑的图像和更少的细节。减小直径允许更多的频率通过,从而产生更清晰的图像和更多的细节。为了达到理想的效果,选择合适的直径是很重要的,因为使用太小的直径会导致过滤器不够有效,而使用太大的直径会导致丢失太多的细节。
一般来说,高斯滤波器由于其平滑性和鲁棒性,更常用于图像处理任务。在某些应用中,需要更尖锐的截止,理想滤波器可能更适合。
利用FFT修改图像频率是一种有效的降低噪声和提高图像锐度的方法。这包括使用FFT将图像转换到频域,使用适当的技术过滤噪声,并使用反FFT将修改后的图像转换回空间域。通过理解和实现这些技术,我们可以提高各种应用程序的图像质量。
https://avoid.overfit.cn/post/8768ec2a60a0456eab327abc33146508
作者:Muhammad Ahmed
相关文章:

Python图像处理:频域滤波降噪和图像增强
图像处理已经成为我们日常生活中不可或缺的一部分,涉及到社交媒体和医学成像等各个领域。通过数码相机或卫星照片和医学扫描等其他来源获得的图像可能需要预处理以消除或增强噪声。频域滤波是一种可行的解决方案,它可以在增强图像锐化的同时消除噪声。 …...

智能手机高端“酣战”,转机在何方?
经过多年发展,如今全世界有七成手机由中国制造,但在利润最丰厚的高端市场,国产厂商在很长一段时间之内都是形单影只,曾经一度跻身高端的“华为”因为封禁成了“绝唱”。 华为“失声”高端之后,其他一众国产厂商或主动…...
K8s pod 动态弹性扩缩容 HPA
一、概述Horizontal Pod Autoscaler(HPA,Pod水平自动伸缩),根据平均 CPU 利用率、平均内存利用率或你指定的任何其他自定义指标自动调整 Deployment 、ReplicaSet 或 StatefulSet 或其他类似资源,实现部署的自动扩展和…...

C++中的类简要介绍
文章目录前言一、什么是类什么是对象1.类的概述2.对象的概述二、如何创建使用类三、class和struct创建类时的区别1.访问级别2.继承方式总结前言 本篇文章讲给大家介绍一个C中重要的概念,了解了这个概念大家就明白了为什么C会叫做面向对象编程了。 一、什么是类什么…...
项目管理工具DHTMLX Gantt灯箱元素配置教程:只读模式
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的大部分开发需求,具备完善的甘特图图表库,功能强大,价格便宜,提供丰富而灵活的JavaScript API接口,与各种服务器端技术&am…...

从LiveData迁移到Kotlin的 Flow,才发现是真的香!
LiveData 对于 Java 开发者、初学者或是一些简单场景而言仍是可行的解决方案。而对于一些其他的场景,更好的选择是使用 Kotlin 数据流 (Kotlin Flow)。虽说数据流 (相较 LiveData) 有更陡峭的学习曲线,但由于它是 JetBrains 力挺的 Kotlin 语言的一部分&…...
【BOOST C++】组件编程(2)-- 组件的设计原理
GitHub - ros2/demos at foxy 一、说明 为了研究ROS2的组件编程,首先要理解如何何为组件。组件本是微软的发明物体,但是在ubuntu上需要自己从底层实现,就说ROS2不用你写,但是就能看明白也是需要一点理论功底的。本篇按照COM内幕的…...

基于单细胞多组学数据无监督构建基因调控网络
在单细胞分辨率下识别基因调控网络(GRNs,gene regulatory networks)一直是一个巨大的挑战,而单细胞多组学数据的出现为构建GRNs提供了机会。 来自:Unsupervised construction of gene regulatory network based on si…...

蓝桥杯-最优清零方案(2022省赛)
蓝桥杯-最优清零方案1、问题描述2、解题思路3、代码实现1、问题描述 给定一个长度为 N 的数列 1,2,⋯,A1,A2,...,ANA_1,A_2,...,A_NA1,A2,...,AN 。现在小蓝想通过若干次操作将 这个数列中每个数字清零。 每次操作小蓝可以选择以下两种之一: 1. 选择一个大于 0 的整数, 将…...
)
Mac免费软件下载网站推荐(最全免费,替代MacWk)
一、Appstorrent 官方网站: https://appstorrent.ru/ 这是一个俄语网站,其他很多网站资源都来自这里。点击右上角切换到中文。不需要登录网站,直接从软件详情页下载即可。体验非常好。 二、Xclient 官方网站: https://xclie…...
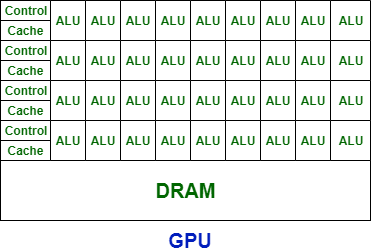
GPU是什么
近期ChatGPT十分火爆,随之而来的是M国开始禁售高端GPU显卡。M国想通过禁售GPU显卡的方式阻挡中国在AI领域的发展。 GPU是什么?GPU(英语:Graphics Processing Unit,缩写:GPU)是显卡的“大脑”&am…...

20230305学习计划
目录 第二天学习开发框架 前言 一、巩固复习第一天20230304学习笔记 二、SpringMVC中的控制器是不是单例模式?如果是,如何保证线程安全? 1、控制器是单例模式,是线程不安全的。 2、Spring中保证线程安全的方法: …...

SocketCan 应用编程
SocketCan 应用编程 由于 Linux 系统将 CAN 设备作为网络设备进行管理,因此在 CAN 总线应用开发方面,Linux 提供了SocketCAN 应用编程接口,使得 CAN 总线通信近似于和以太网的通信,应用程序开发接口更加通用,也更加灵…...

从零学习python - 04函数方法与返回值
函数:Function-也称为方法,是组织好的、可重复使用的,用来实现指定功能的代码块。函数的定义与调用:创建函数目的是封装业务逻辑,实现代码复用# 创建函数关键字:def(definition)def fun1(x, y):print(x y)函数的参数:python函数中…...
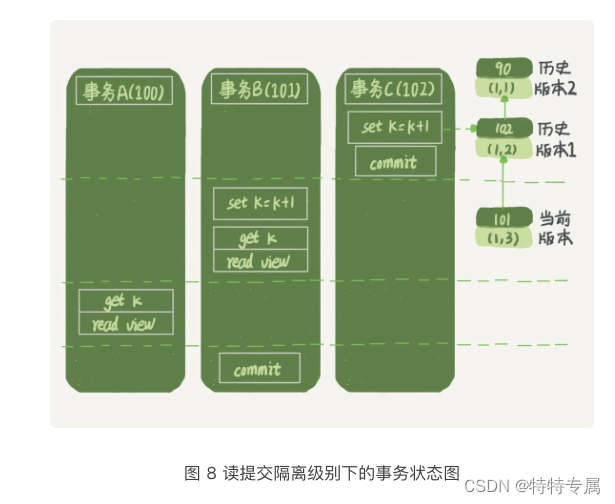
MySQL实战之事务到底是隔离的还是不隔离的
1.前言 我们在MySQL实战之事务隔离:为什么你改了我还看不见讲过事务隔离级别的时候提到过,如果是可重复读隔离级别,事务T启动的时候会创建一个视图read-view,之后事务T执行期间,即使有其他事务修改了数据,事务T看到的…...
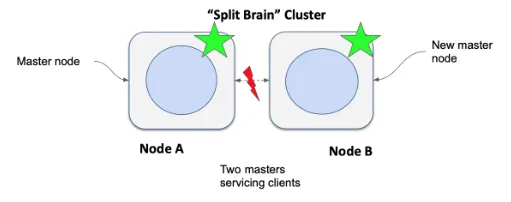
Elasticsearch:理解 Master,Elections,Quorum 及 脑裂
集群中的每个节点都可以分配多个角色:master、data、ingest、ml(机器学习)等。 我们在当前讨论中感兴趣的角色之一是 master 角色。 在 Elasticsearch 的配置中,我们可以配置一个节点为 master 节点。master 角色的分配表明该节点…...
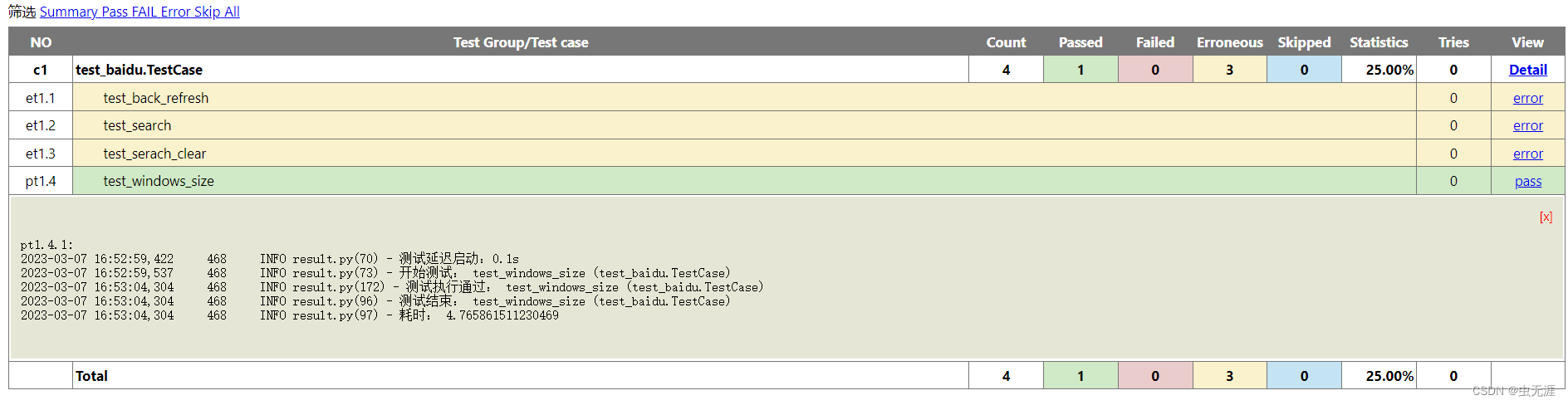
【致敬女神】HTMLReport应用之Unittest+Python+Selenium+HTMLReport项目自动化测试实战
HTMLReport应用之UnittestPythonSeleniumHTMLReport项目自动化测试实战1 测试框架结构2 技术栈3 实现思路3.1 使用HtmlTestRunner3.2 使用HTMLReport4 TestRunner参数说明4.1 源码4.2 参数说明5 框架代码5.1 common/reportOut.py5.2 common/sendMain.py5.3 report5.3.1 xxx.htm…...

JAVA的16 个实用代码优化小技巧
一、类成员与方法的可见性最小化 举例:如果是一个private的方法,想删除就删除。 如果一个public的service方法,或者一个public的成员变量,删除一下,不得思考很多。 二、使用位移操作替代乘除法 计算机是使用二进制…...

并发编程的三大挑战之原子性及其解决方案
目录 一、原子性问题 1、带来原子性问题的原因 2、如何解决线程切换带来的原子问题 2.1、使用synchronized关键字来保证 2.2、使用CAS来保证原子性 2.3、使用lock锁来保证 一、原子性问题 1、带来原子性问题的原因 线程切换是带来原子的根本原因,java的并发程…...
)
QML动画(其他的动画)
PauseAnimation (暂停动画) 为动画提供暂停 Rectangle{id:rect1width: 100;height: 100;x:100;y:100color: "lightBlue"SequentialAnimation{running: trueColorAnimation {target: rect1;property: "color";…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
