【动态规划 区间dp 位运算】100259. 划分数组得到最小的值之和
本文涉及知识点
动态规划 区间dp 位运算
LeetCode100259. 划分数组得到最小的值之和
给你两个数组 nums 和 andValues,长度分别为 n 和 m。
数组的 值 等于该数组的 最后一个 元素。
你需要将 nums 划分为 m 个 不相交的连续 子数组,对于第 ith 个子数组 [li, ri],子数组元素的按位AND运算结果等于 andValues[i],换句话说,对所有的 1 <= i <= m,nums[li] & nums[li + 1] & … & nums[ri] == andValues[i] ,其中 & 表示按位AND运算符。
返回将 nums 划分为 m 个子数组所能得到的可能的 最小 子数组 值 之和。如果无法完成这样的划分,则返回 -1 。
示例 1:
输入: nums = [1,4,3,3,2], andValues = [0,3,3,2]
输出: 12
解释:
唯一可能的划分方法为:
[1,4] 因为 1 & 4 == 0
[3] 因为单元素子数组的按位 AND 结果就是该元素本身
[3] 因为单元素子数组的按位 AND 结果就是该元素本身
[2] 因为单元素子数组的按位 AND 结果就是该元素本身
这些子数组的值之和为 4 + 3 + 3 + 2 = 12
示例 2:
输入: nums = [2,3,5,7,7,7,5], andValues = [0,7,5]
输出: 17
解释:
划分 nums 的三种方式为:
[[2,3,5],[7,7,7],[5]] 其中子数组的值之和为 5 + 7 + 5 = 17
[[2,3,5,7],[7,7],[5]] 其中子数组的值之和为 7 + 7 + 5 = 19
[[2,3,5,7,7],[7],[5]] 其中子数组的值之和为 7 + 7 + 5 = 19
子数组值之和的最小可能值为 17
示例 3:
输入: nums = [1,2,3,4], andValues = [2]
输出: -1
解释:
整个数组 nums 的按位 AND 结果为 0。由于无法将 nums 划分为单个子数组使得元素的按位 AND 结果为 2,因此返回 -1。
提示:
1 <= n == nums.length <= 104
1 <= m == andValues.length <= min(n, 10)
1 <= nums[i] < 105
0 <= andValues[j] < 105
动态规划的位运算
f(i,j) = & = x : i j \Large\And=_{x:i}^j &=x:ij
vNext[cur] 记录符合以下条件之一的next:
一,next-1 < cur。
二,f(i,next) ≠ \neq = f(i,next-1)。
iBitCnt = log(max(nums[i]) ≈ \approx ≈ 22 ,显然next的数量不会超过iBitCnt。
如果f(i,j)发生变化,至少一个二进制1变成0。
动态规划
动态规划的状态表示
dp[len][cur] 表示将nums[0…cur]划分为len个区间的最小和。
空间复杂度:O(nm)
动态规划的转移方程
r个区间向r+1个区间转移时:
如果f(cur,next) 等于 andValues[r-1]则:
MinSelf(dp[r+1][x],dp[r][cur-1]+nums[x]) x ∈ [ n e x t , n e x t 的下一个值 ) 这样值设置的时间复杂度是: \in[next,next的下一个值) 这样值设置的时间复杂度是: ∈[next,next的下一个值)这样值设置的时间复杂度是: O ( m × n × i B i t C n t × n ) O(m \times n \times iBitCnt \times n ) O(m×n×iBitCnt×n) ,超时了。
只更新:x = next,其它的用二种方式更新:
如果 (nums[cur]& andValues[r-1]) = andValues[r-1]
则MinSelf(dp[r][cur],dp[r][cur-1])
时间复杂度:$ O ( m × n × i B i t C n t ) O(m \times n \times iBitCnt ) O(m×n×iBitCnt)
动态规划的初始值
枚举第一个区间
动态规范的返回值
dp.back().back()
动态规划的填表顺序
len 从1到m_r-1。
cur从1到m_c-1
代码
核心代码
template<class ELE,class ELE2>
void MinSelf(ELE* seft, const ELE2& other)
{*seft = min(*seft,(ELE) other);
}template<class ELE>
void MaxSelf(ELE* seft, const ELE& other)
{*seft = max(*seft, other);
}class Solution {
public:int minimumValueSum(vector<int>& nums, vector<int>& andValues) {const int iBitCnt = 22;m_r = andValues.size();m_c = nums.size();const int iMax = (1 << iBitCnt) - 1;vector<vector<int>> dp(m_r+1,vector<int>(m_c, m_iNotMay));int iAnd = iMax;for (int i = 0; i < m_c; i++) {iAnd &= nums[i];if (iAnd == andValues[0]) {dp[1][i] = nums[i];}}vector<set<int>> vNext(m_c);{vector<int> next(iBitCnt, m_c);for (int i = nums.size() - 1; i >= 0; i--) {vNext[i] = set<int>(next.begin(), next.end());vNext[i].emplace(i);vNext[i].erase(m_c);for (int bit = 0; bit < iBitCnt; bit++){bool b = (1 << bit) & nums[i];if (!b) {next[bit] = i;}}}}for (int r = 1; r < m_r; r++){for (int cur = 1; cur < m_c; cur++){int iAdd = iMax;for (const auto& next : vNext[cur]) {iAdd &= nums[next];if (andValues[r] == iAdd) {MinSelf(&dp[r + 1][next], dp[r][cur - 1] + nums[next]);}}if ((andValues[r - 1] & nums[cur]) == andValues[r - 1]) {MinSelf(&dp[r][cur], dp[r][cur - 1]+nums[cur]-nums[cur-1]);} } }{int r = m_r;for (int cur = 1; cur < m_c; cur++){ if ((andValues[r - 1] & nums[cur]) == andValues[r - 1]) {MinSelf(&dp[r][cur], dp[r][cur - 1] + nums[cur] - nums[cur - 1]);}}}const int iRet = dp.back().back();return (iRet >= 1'000'000) ? -1 : iRet;}int m_r,m_c;const int m_iNotMay = 1'000'000'000;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{vector<int> nums, andValues;int k;{Solution sln;nums = { 1, 9, 8, 8 }, andValues = { 1,8 };auto res = sln.minimumValueSum(nums, andValues);Assert(9, res);}{Solution sln;nums = { 1, 3, 2, 4, 7, 5, 3 }, andValues = { 0, 5, 3 };auto res = sln.minimumValueSum(nums, andValues);Assert(12, res);}{Solution sln;nums = { 1, 4, 3, 3, 2 }, andValues = { 0, 3, 3, 2 };auto res = sln.minimumValueSum(nums, andValues);Assert(12, res);}//vector<int> nums = { 3,6,9 };//int k;////{// Solution sln;// nums = { 3,6,9 }, k = 3;// auto res = sln.findKthSmallest(nums, k);// Assert(9LL, res);//}}

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划 区间dp 位运算】100259. 划分数组得到最小的值之和
本文涉及知识点 动态规划 区间dp 位运算 LeetCode100259. 划分数组得到最小的值之和 给你两个数组 nums 和 andValues,长度分别为 n 和 m。 数组的 值 等于该数组的 最后一个 元素。 你需要将 nums 划分为 m 个 不相交的连续 子数组,对于第 ith 个子数…...
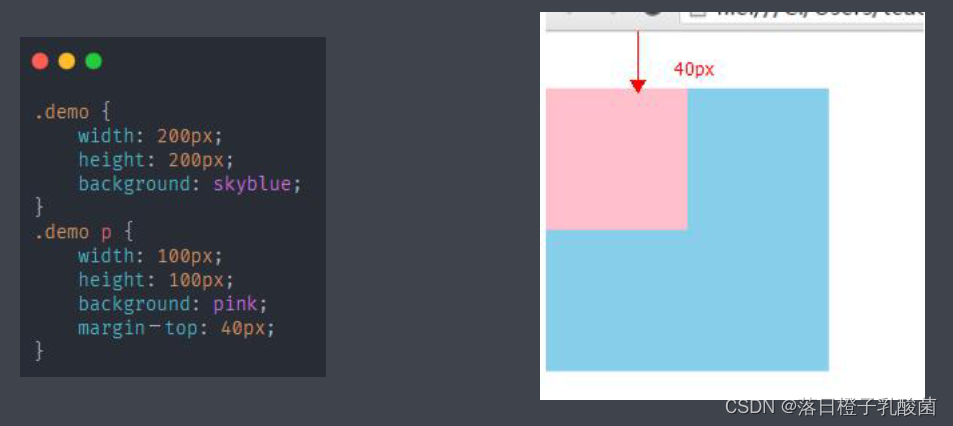
CSS核心样式-02-盒模型属性及扩展应用
目录 三、盒模型属性 常见盒模型区域 盒模型图 盒模型五大属性 1. 宽度 width 2. 高度 height 3. 内边距 padding 四值法 三值法 二值法 单值法 案例 4. 边框 border 按照属性值的类型划分为三个单一属性 ①线宽 border-width ②线型 border-style ③边框颜色 bo…...
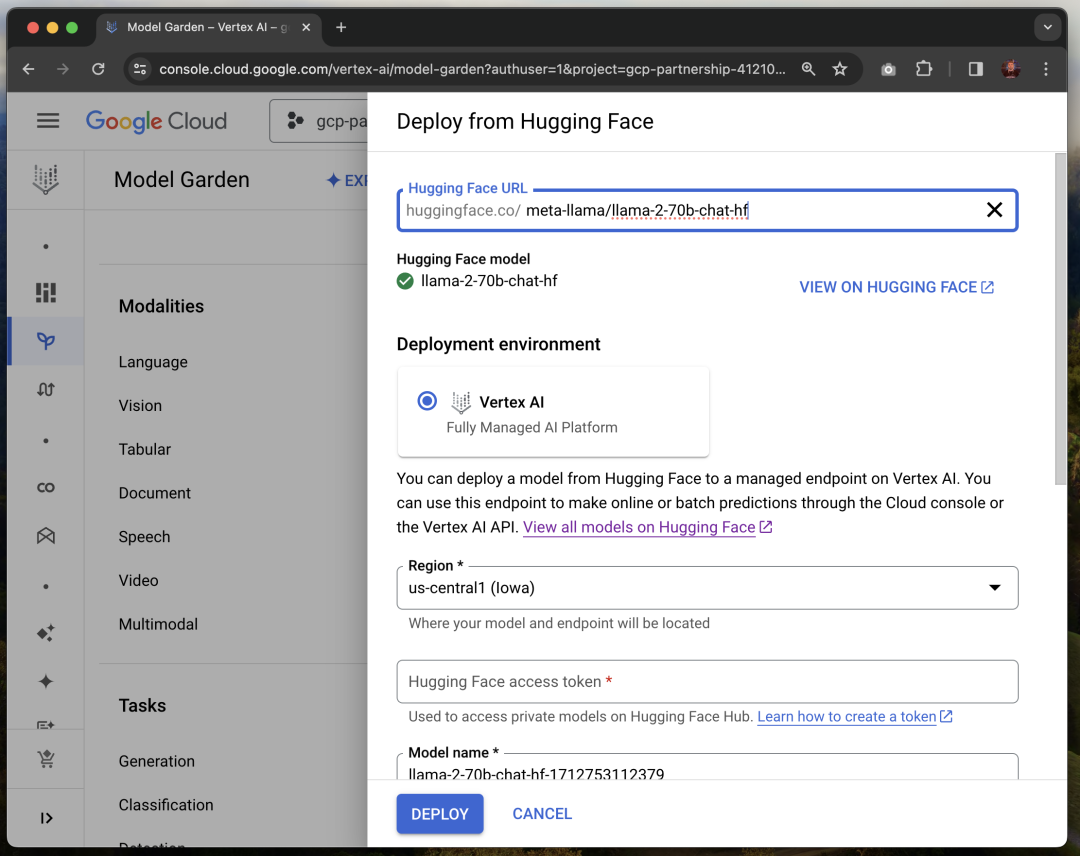
在 Google Cloud 上轻松部署开放大语言模型
今天,“在 Google Cloud 上部署”功能正式上线! 这是 Hugging Face Hub 上的一个新功能,让开发者可以轻松地将数千个基础模型使用 Vertex AI 或 Google Kubernetes Engine (GKE) 部署到 Google Cloud。 Model Garden (模型库) 是 Google Clou…...

005Node.js模块URL的使用
引入 URL 模块 要使用 URL 模块,首先需要在代码中引入它。可以使用以下代码将 URL 模块导入到你的脚本中: const url require(url);实例代码 const urlrequire(url); var apihttp://www.baidu.com?nameshixiaobin&age20; console.log(url.parse(…...

美团笔试复盘
昨天做了美团的笔试,现在复盘一下。 1、将数组按照绝对值大小排序 有道算法题解决思路需要将数组按照绝对值大小进行排序,我使用的是sort方法Comparator比较器实现的,这里记录一下: public static void main(String[] args) {In…...
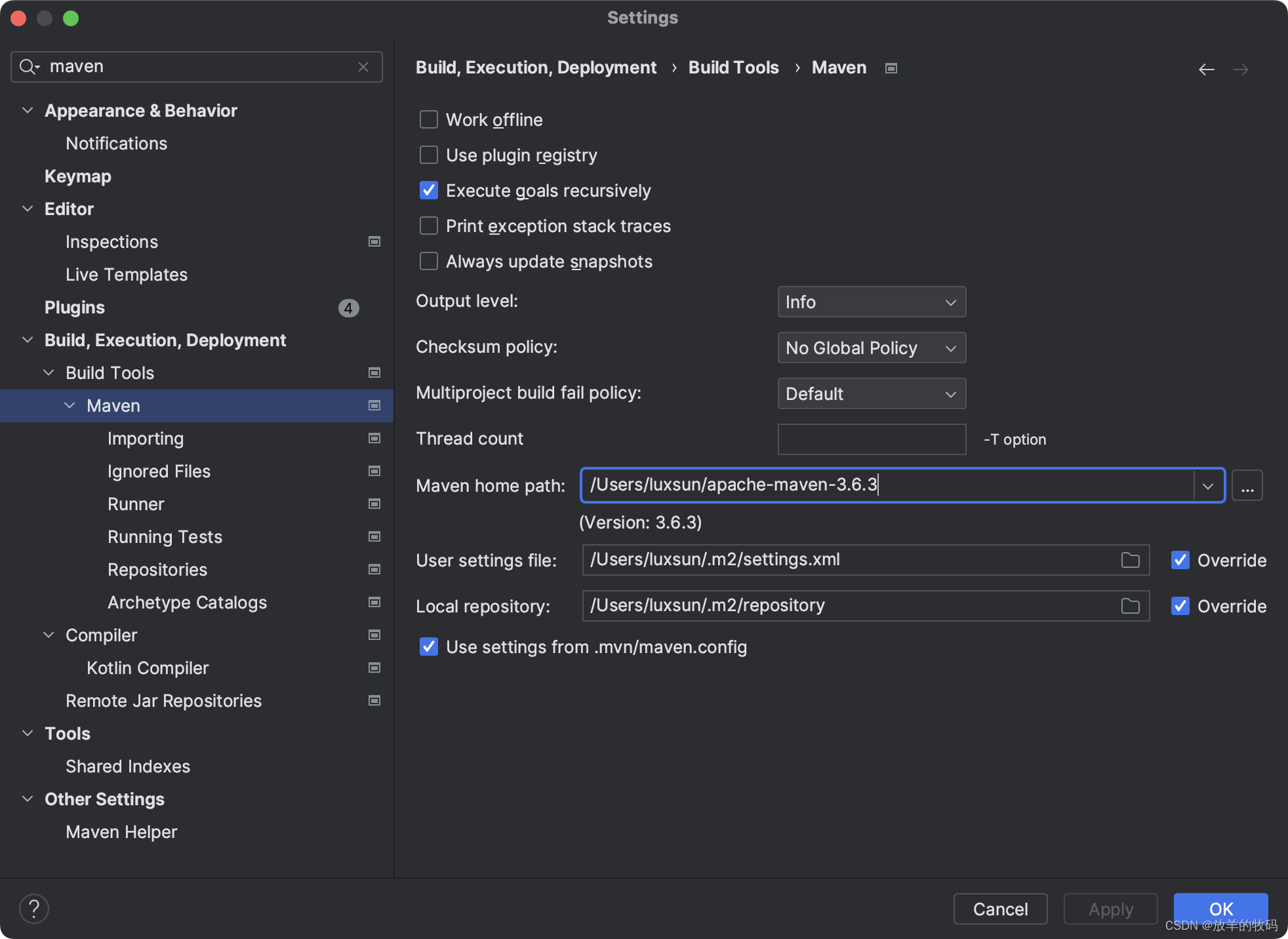
IntelliJ IDEA - Since Maven 3.8.1 http repositories are blocked
问题描述 新下载的 IDEA 在构建项目时,在下载引用的包时出现 “Since Maven 3.8.1 http repositories are blocked” 的问题。 原因分析 从 Maven 3.8.1 开始,不再支持 http 的包了。由于现在对网络安全的日益重视,都在向 https 转变&#…...
流程)
Django的APP应用更名(重命名)流程
将Django中的一个现有APP更名是一个需要谨慎操作的过程,因为它涉及到多个文件和配置的更新。下面是详细的步骤和一些补充细节,帮助你更顺利地完成APP重命名: 1. 修改APP名称及相关引用 更改APP目录名称: 首先,重命名…...

ChatGLM3-6B大语言模型离线执行
ChatGLM3-6B大语言模型离线执行 模型准备 一般而言,模型和模型参数可以通过如下三个模型源进行相应的下载: HuggingFace | ModelScope | WiseModel 本实例中,使用的是HuggingFace的源下载,相应的地址如下: HuggingFa…...
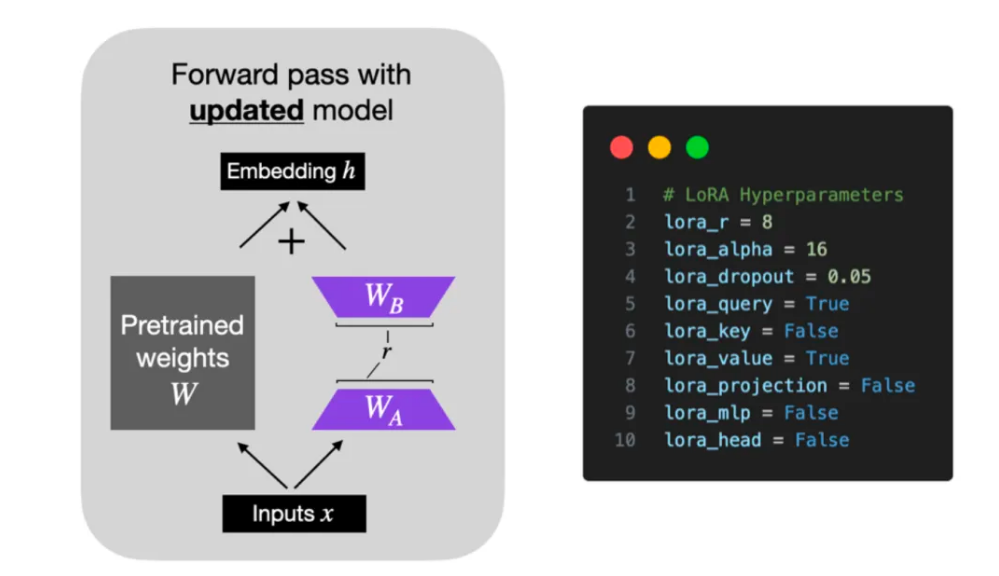
了解大语言模型的参数高效微调(Parameter-Effcient Fine-Tuning)
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 大语言模型在众多应用领域实现了突破性的进步,显著提升了各种任务的完成度。然而,其庞大的规模也带来了高昂的计算成本。这些模型往往包含数十亿甚至上千亿参数,需要…...

2024.4.14力扣每日一题——设计哈希集合
2024.4.14 题目来源我的题解方法一 链表数组 题目来源 力扣每日一题;题序:705 我的题解 方法一 链表数组 由于给定限制次数为10000,所以构造一个长度为10001的链表数组。对于add操作先看数组对应的位置是否为null或者为空,若是…...

SQL explain 显示子查询A类型为ALL怎么优化
当 SQL EXPLAIN 显示子查询 A 的类型为 ALL 时,这意味着数据库系统正在执行全表扫描,而不是使用索引来执行子查询。全表扫描可能会导致性能下降,特别是在大型表上。 为了优化这种情况,您可以考虑以下几点: 1. **索引…...

网络协议学习——IP协议
IP(Internet Protocol,互联网协议)是网络中最基本的协议之一,负责在互联网中进行数据包的传输。下面是对IP协议的详细讲解: IP协议的作用 IP协议是在网络层(第三层)上工作的协议,它的…...
—— 基础知识和功能介绍)
MATLAB初学者入门(1)—— 基础知识和功能介绍
MATLAB(Matrix Laboratory)是一种用于数值计算、可视化以及编程的高性能语言环境。它广泛应用于工程、科学研究和教育等领域。以下是对MATLAB基础知识和编程技巧的系统性讲解,分为几个主要部分: 1. 基础操作 变量和表达式 在MAT…...

React Css 四种引入方式
React CSS 内联样式 优点 样式之间不会有冲突可以动态获取组件中state的值 缺点 要使用驼峰标识部分样式没有很友好的提示如果大量去写内敛样式 容易造成代码混乱伪类和伪元素无法编写 class HighCom extends PureComponent {constructor(props) {super(props)this.state…...

题目:输入3个数a,b,c,按大小顺序输出。
题目:输入3个数a,b,c,按大小顺序输出。 There is no nutrition in the blog content. After reading it, you will not only suffer from malnutrition, but also impotence. The blog content is all parallel goods. Those who are worried abou…...
AI预测体彩排3第3弹【2024年4月14日预测--第1套算法开始计算第3次测试】
今天咱们继续测试第1套算法和模型,今天是第3次测试,目前的测试只是为了记录和验证,不建议大家盲目跟买。我的目标仍旧是10次命中3-4次!~废话不多说了,直接上结果! 2024年4月14日排3的七码预测结果如下 第一套&…...

Android 在xml 布局中如何嵌套 Jetpack Compose
最近在项目开发的过程中需要用到 Jetpack Compose,之前没有接触过Compose,所以项目一直没有用到Compose。通过查看官网发现Compose上手比较快,但是准备比较复杂的布局要转换成Compose 不是一件容易的事情。那有没有可能只是对成熟的项目中的x…...

Spring Boot统一功能处理(一)
本篇主要介绍Spring Boot的统一功能处理中的拦截器。 目录 一、拦截器的基本使用 二、拦截器实操 三、浅尝源码 初始化DispatcherServerlet 处理请求(doDispatch) 四、适配器模式 一、拦截器的基本使用 在一般的学校或者社区门口,通常会安排几个…...

我与C++的爱恋:类与对象(二)
🔥个人主页:guoguoqiang. 🔥专栏:我与C的爱恋 本篇着重介绍构造函数和析构函数,剩余内容在下篇解答。 一、类的默认成员函数 如果一个类中什么成员都没有,简称为空类。 任何类在什么都不写时…...

BERT入门:理解自然语言处理中的基本概念
1. 自然语言处理简介 自然语言处理(Natural Language Processing,NLP)是人工智能领域的重要分支,涉及计算机与人类自然语言之间的相互作用。NLP 的应用已经深入到我们日常生活中的方方面面,如智能助理、机器翻译、舆情…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
