数据结构复习指导之绪论(算法的概念以及效率的度量)
文章目录
绪论:
2.算法和算法评价
知识总览
2.1算法的基本概念
知识点回顾与重要考点
2.2算法效率的度量
知识总览
1.时间复杂度
2.空间复杂度
知识点回顾与重要考点
归纳总结
绪论:
2.算法和算法评价
知识总览
2.1算法的基本概念
算法( Algorithm)是对特定问题求解步骤的一种描述,它是指令的有限序列,其中的每条指令表示一个或多个操作。此外,一个算法还具有下列五个重要特性:
1) 有穷性。一个算法必须总在执行有穷步之后结束,且每一步都可在有穷时间内完成。

2)确定性。算法中每条指令必须有确切的含义,对于相同的输入只能得出相同的输出。
3)可行性。算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
4)输入。一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
5)输出。一个算法有一个或多个输出,这些输出是与输入有着某种特定关系的量。通常,设计一个“好”的算法应考虑达到以下目标:
1) 正确性。算法应能够正确地解决求解问题。
2)可读性。算法应具有良好的可读性,以帮助人们理解。

3)健壮性。算法能对输入的非法数据做出反应或处理,而不会产生莫名其妙的输出。
4)高效率与低存储量需求。效率是指算法执行的时间,存储量需求是指算法执行过程中所
需要的最大存储空间,这两者都与问题的规模有关。

知识点回顾与重要考点

2.2算法效率的度量
知识总览

1.时间复杂度
一个语句的频度是指该语句在算法中被重复执行的次数。算法中所有语句的频度之和记为T(n),它是该算法问题规模n的函数,时间复杂度主要分析T(n)的数量级。
算法中基本运算(最深层循环中的语句)的频度与T(n)同数量级,因此通常将算法中基本运算的执行次数的数量级作为该算法的时间复杂度。于是,算法的时间复杂度记为T(n)=O(f(n))
式中,O的含义是T(n)的数量级,其严格的数学定义是:若T(n)和 fn)是定义在正整数集合上的两个函数,则存在正常数C和n,使得当n≥n时,都满足0≤T(n)≤Cf(n)。
算法的时间复杂度不仅依赖于问题的规模n,也取决于待输入数据的性质(如输入数据元素的初始状态)。例如,在数组A [ 0...n- 1]中,查找给定值k的算法大致如下:
i=n-l;
while (i>=0&&(A[i]!=k))
i--;
return i;该算法中语句3(基本运算)的频度不仅与问题规模n有关,而且与下列因素有关:
若A中没有与k相等的元素,则语句3的频度f(n)=n。
②若A的最后一个元素等于k,则语句3的频度f(n)是常数0。最坏时间复杂度是指在最坏情况下,算法的时间复杂度。
平均时间复杂度是指所有可能输入实例在等概率出现的情况下,算法的期望运行时间。
最好时间复杂度是指在最好情况下,算法的时间复杂度。
一般总是考虑在最坏情况下的时间复杂度,以保证算法的运行时间不会比它更长。在分析一个程序的时间复杂性时,有以下两条规则:
1)加法规则:T(n)=T(n)+T,(n)=O(f(n))+O(gn))=O(max(f(n), g(n))
2)乘法规则: T(n)=T(n)xT;(n)=O(f(n))×O(g(n))=o(f (n)×g(n))

2.空间复杂度
算法的空间复杂度S(n)定义为该算法所需的存储空间,它是问题规模n的函数,记为
S(n)=O(g(n))
一个程序在执行时除需要存储空间来存放本身所用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。若输入数据所占空间只取决于问题本身,和算法无关,则只需分析除输入和程序之外的额外空间。例如,若算法中新建了几个与输入数据规模n相同的辅助数组,则空间复杂度为O(n)。
算法原地工作是指算法所需的辅助空间为常量,即O(1)。




知识点回顾与重要考点

归纳总结
本章的重点是分析程序的时间复杂度。一定要掌握分析时间复杂度的方法和步骤,很多读者
在做题时一眼就能看出在厅出的两种形式,供大家参考。人众多资料,总结出了此类题型的两种形式,供大家参考。
1.循环主体中的变量参与循环条件的判断
在用于递推实现的算法中,首先找出基本运算的执行次数x与问题规模n之间的关系式,解得x=f(n),f(n)的最高次幂为k,则算法的时间复杂度为。例如,
1.
int i=1;
while(i<=n)
i=i*2;2.
int y=5;
while((y+1)*(y+1)<n)
y=y+1;
在例1中,设基本运算i=i*2的执行次数为t,则,解得
,故
在例2中,设基本运算y=y+1的执行次数为t,则t=y-5,且(t+5+1)(t+5+1)<n,解得t<√n-6,即 T(n)= O( √n )。
2.循环主体中的变量与循环条件无关
此类题可采用数学归纳法或直接累计循环次数。多层循环时从内到外分析,忽略单步语句、条件判断语句,只关注主体语句的执行次数。
此类问题又可分为递归程序和非递归程序:
·递归程序一般使用公式进行递推。时间复杂度的分析如下:
T(n)=1+T(n-1)=1+1+T(n-2)=…=n-1+ T(1)
即T(n)=O(n)
·非递归程序的分析比较简单,可以直接累计次数。
相关文章:
数据结构复习指导之绪论(算法的概念以及效率的度量)
文章目录 绪论: 2.算法和算法评价 知识总览 2.1算法的基本概念 知识点回顾与重要考点 2.2算法效率的度量 知识总览 1.时间复杂度 2.空间复杂度 知识点回顾与重要考点 归纳总结 绪论: 2.算法和算法评价 知识总览 2.1算法的基本概念 算法( Al…...
)
C语言经典例题(23)
1.求n的阶乘。(不考虑溢出) #include <stdio.h>int fac(int n);int main() {int n 0;scanf("%d", &n);int sum fac(n);printf("%d", sum);return 0; }int fac(int n) {if (n > 1){return n * fac(n - 1);}elsereturn 1; }2.求第n个斐波那契…...

Gitea的简单介绍
Gitea 是一个自由、开源、轻量级的 Git 服务程序。它是为了建立一个易于使用的、类似 GitHub 的 Git 服务而创建的。Gitea 采用 Go 语言编写,具有简单、快速、易于安装和配置的特点。 Gitea 提供了一个基本的 Web 界面,可以方便地进行代码托管、问题跟踪、协作等操作。用户可…...

Qt信号与槽
我们在使用Qt的时候,不使用Qt Designer 的方式进行开发,使用ui文件,信号与槽的连接方式是生成代码之后才能在setupUi函数里才能看到,或者需要进入Ui设计器里的信号槽模式里才能看到信号槽的连接。所以我们最好使用代码绘制界面。 …...
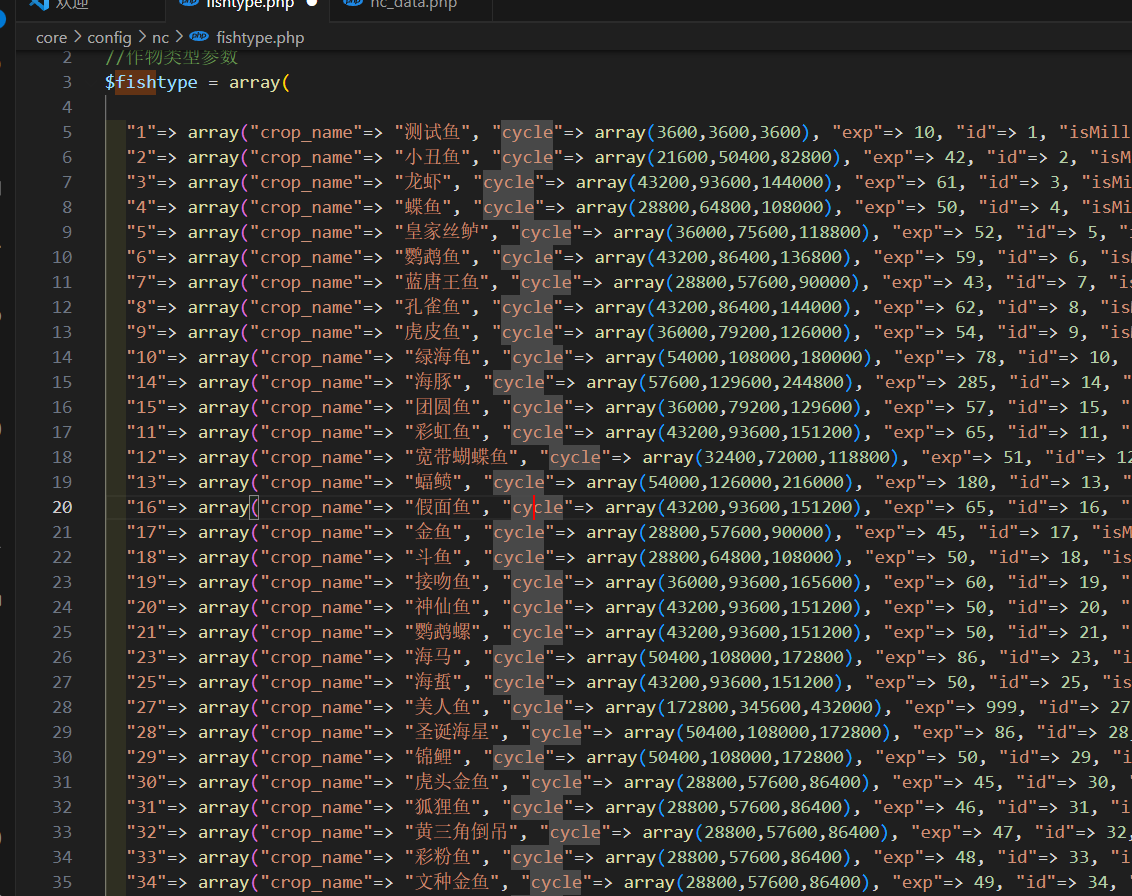
QQ农场-phpYeFarm添加数据教程
前置知识 plugin\qqfarm\core\data D:\study-project\testweb\upload\source\plugin\qqfarm\core\data 也就是plugin\qqfarm\core\data是一个缓存文件,如果更新农场数据后,必须要删除才可以 解决种子限制(必须要做才可以添加成功) 你不更改加入了id大于2000直接删除种子 D…...
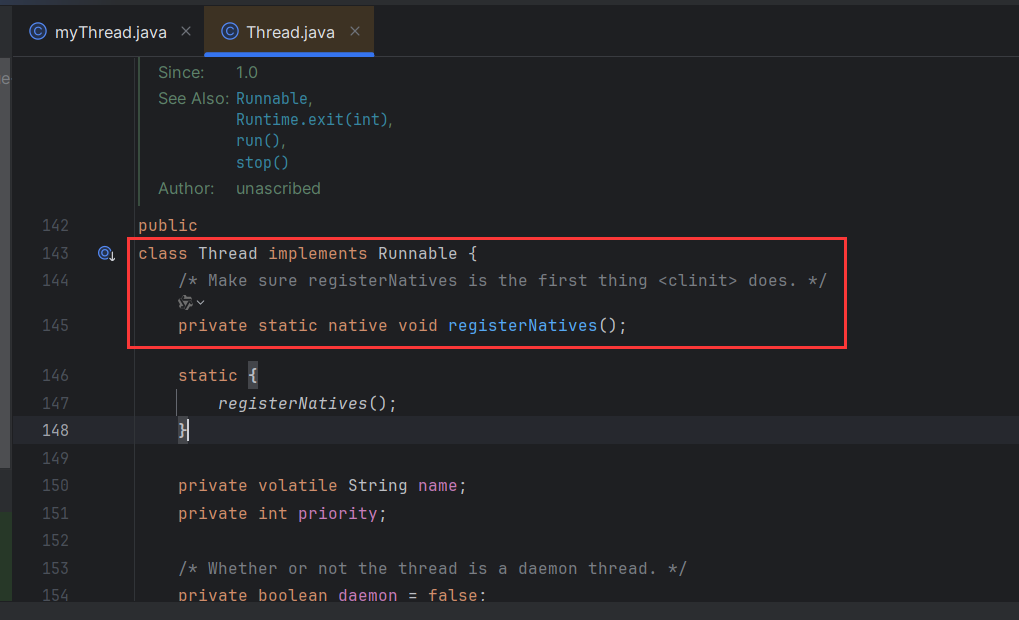
Java中创建多线程的方法
继承Thread类,对该类进行new一个实例,对实例调用start方法,重写run方法。 缺点:单继承,无法继承 public class myThread extends Thread {public static void main(String[] args) {myThread myThread new myThread()…...

MT3020 任务分配
思路:利用二分找到某个时间是满足“k个人可以完成” ,并且时间最小。 因为尽量让后面的人做任务,所以从后往前排任务(倒着分配)。从后往前遍历任务,如果此人加上这个任务超出之前求得的时间,就…...

【Redis】事务
Redis事务是一组命令的集合。这组命令顺序化执行而不会被其他命令插入。 Redis事务命令 命令描述DISCARD取消事务,放弃执行EXEC执行事务MULTI标记事务的开始UNWATCH取消WATCH对所有key的监控WATCH监控所有key Redis事务特点 特点说明单独的隔离操作Redis命令执行…...

每日一题(leetcode238):除自身以外数组的乘积--前缀和
不进阶是创建两个数组: class Solution { public:vector<int> productExceptSelf(vector<int>& nums) {int nnums.size();vector<int> left(n);vector<int> right(n);int mul1;for(int i0;i<n;i){mul*nums[i];left[i]mul;}mul1;for…...
内网通如何去除广告,内网通免广告生成器
公司使用内网通内部传输确实方便!但是会有广告弹窗推送!这个很烦恼!那么如何去除广告呢! 下载: 链接:https://pan.baidu.com/s/1CVVdWexliF3tBaFgN1W9aw?pwdhk7m 提取码:hk7m ID:…...

视频知识整理
1 视频播放器原理 视频播放器播放一个互联网上的视频文件,需要经过以下几个步骤: 解协议:将流媒体协议的数据,解析为标准的相应的封装格式数据 解封装:将封装格式的数据,分离成为音频流压缩编码数据和视…...
【2024】使用Rancher管理k8s集群和创建k8s集群
Rancher管理k8s集群及创建k8s集群。 Rancher版本为:2.8.2目录 rancher管理k8s集群rancher创建k8s集群rancher管理k8s集群 使用rancher管理已经存在的k8s集群。 本部分内容需要自行准备好k8s集群及rancher平台,部署请看本人其他文章 。 登录到rancher平台后,点击集群管理,…...

生成对抗网络 – Generative Adversarial Networks | GAN
目录 生成对抗网络 GAN 的基本原理 非大白话版本 第一阶段:固定「判别器D」,训练「生成器G」...

基于深度学习的生活垃圾智能分类系统(微信小程序+YOLOv5+训练数据集+开题报告+中期检查+论文)
摘要 本文基于Python技术,搭建了YOLOv5s深度学习模型,并基于该模型研发了微信小程序的垃圾分类应用系统。本项目的主要工作如下: (1)调研了移动端垃圾分类应用软件动态,并分析其优劣势;分析了深…...

软件包名生成参考
服务名称-分支名称-最后提交时间(精确到秒)-最后提交-编译时间(unix时间戳) 示例:crm_5.2_221024-221020160306-b846f829-1665655859 包名生成脚本参考: 分支名称 export GIT_BRANCH$(git branch|grep "\*"|head -n1|awk {print $NF})git最…...
)
八大排序算法(面试被问到)
1.八大排序算法都是什么? 八大排序算法有:插入排序、冒泡排序、归并排序、选择排序、快速排序、希尔排序、堆排序、基数排序(通常不提)。此外,还可以直接调用Arrays.sort()进行排序。 2.八大排序算法时间复杂度和稳定…...

SCP指令详细使用介绍
SCP(Secure Copy Protocol)是一种用于在计算机之间安全地传输文件的协议。它通过加密的方式在网络上安全地复制文件。SCP基于SSH(Secure Shell)协议,因此它提供了加密的连接和身份验证,确保数据在传输过程中…...

《前端面试题》- JS基础 - 防抖和节流
在界面触发点击,滚动,输入校验等事件时,如果对事件的触发频率不加以限制,会给浏览器增加负担,且对用户不友好。防抖和节流就是针对类似情况的解决方案。 防抖 防抖(debounce):当连续触发事件时࿰…...
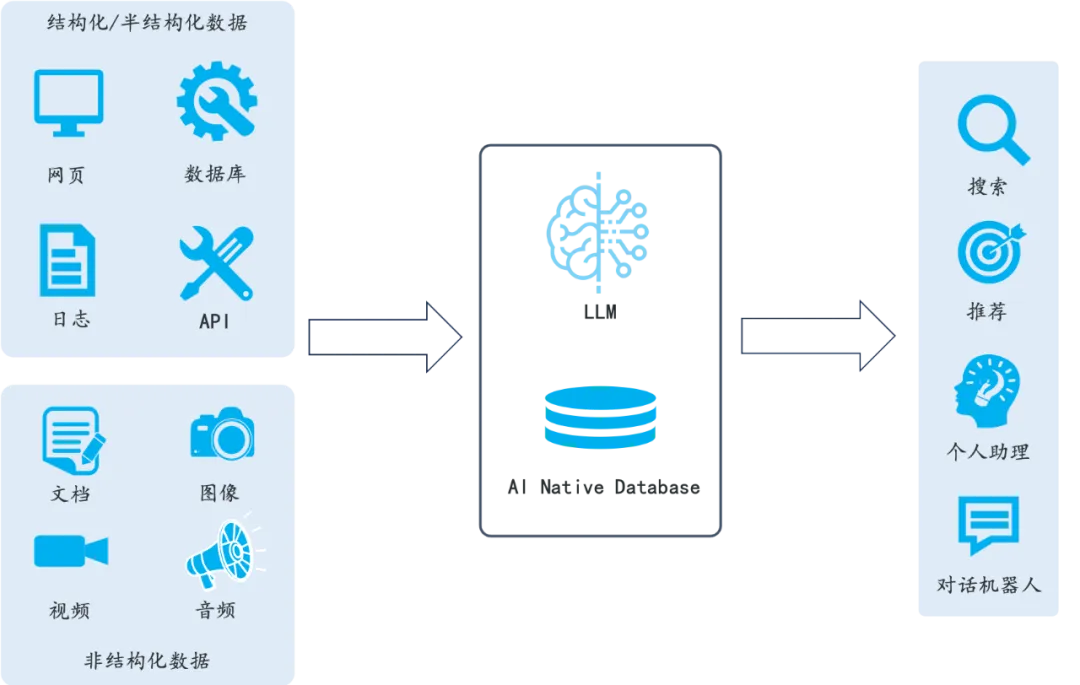
RAGFlow:基于OCR和文档解析的下一代 RAG 引擎
一、引言 在人工智能的浪潮中,检索增强生成(Retrieval-Augmented Generation,简称RAG)技术以其独特的优势成为了研究和应用的热点。RAG技术通过结合大型语言模型(LLMs)的强大生成能力和高效的信息检索系统…...

正则表达式|*+?
在理解编程语言和编译技术的上下文中,了解正则表达式(regular expressions)和正则集(regular sets)的概念是非常重要的。这些概念主要用于描述一组字符串的模式,广泛应用于词法分析中识别各类标记ÿ…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
