C++ 算法主题系列之集结0-1背包问题的所有求解方案
1. 前言
背包问题是类型问题,通过对这一类型问题的理解和掌握,从而可以归纳出求解此类问题的思路和模板。
背包问题的分类有:
0-1背包问题,也称为不可分割背包问题。- 无限背包问题。
- 判定性背包问题.
- 带附属关系的背包问题。
- 双背包求最优值.
- 构造三角形问题.
- 带上下界限制的背包问题(
012背包) - ……
本文将介绍0-1背包问题的各种求解方案,通过对各种求解方案的研究,从而全方面了解0-1背包问题的本质。
2. 0-1 背包问题
问题描述:
有一背包,能容纳的重量为 m,现有 n种物品,每种物品有重量和价值 2 个属性。请设计一个算法,在不分割物品的情况下,保证背包中所容纳的物品的总价值是最大的。
0-1背包也称为完全背包或不可分割背包问题,是一类常见的背包问题。常用的实现方案有递归和动态规划 。
2.1 递归算法
可以有 3 种写法。
2.1.1 第一种递归回溯方案
回顾递归回溯算法适合的问题域:
- 待解决的问题可以分多步。如迷宫问题、排列组合问题……
- 每一步都可能存在多个选择,当某一个选择行不通,或此选择结束后,可以回溯到上一步再另行选择。
那么背包问题是否适合上述的要求?
- 可以想象背包里有很多个格间。当每一个格间填充完毕,则表示得到一种求解。
- 对于格间而言,每一种物品都是一种选择,可以通地回溯再选择另一个物品。
- 其本质是对物品进行任意组合,然后再选择总价值最大的一种组合。
如下图,有 3 个物品需要放置入容量为 50 的背包中。初始可把背包想象成一个大格间,此时可以试着放入物品中的一个。
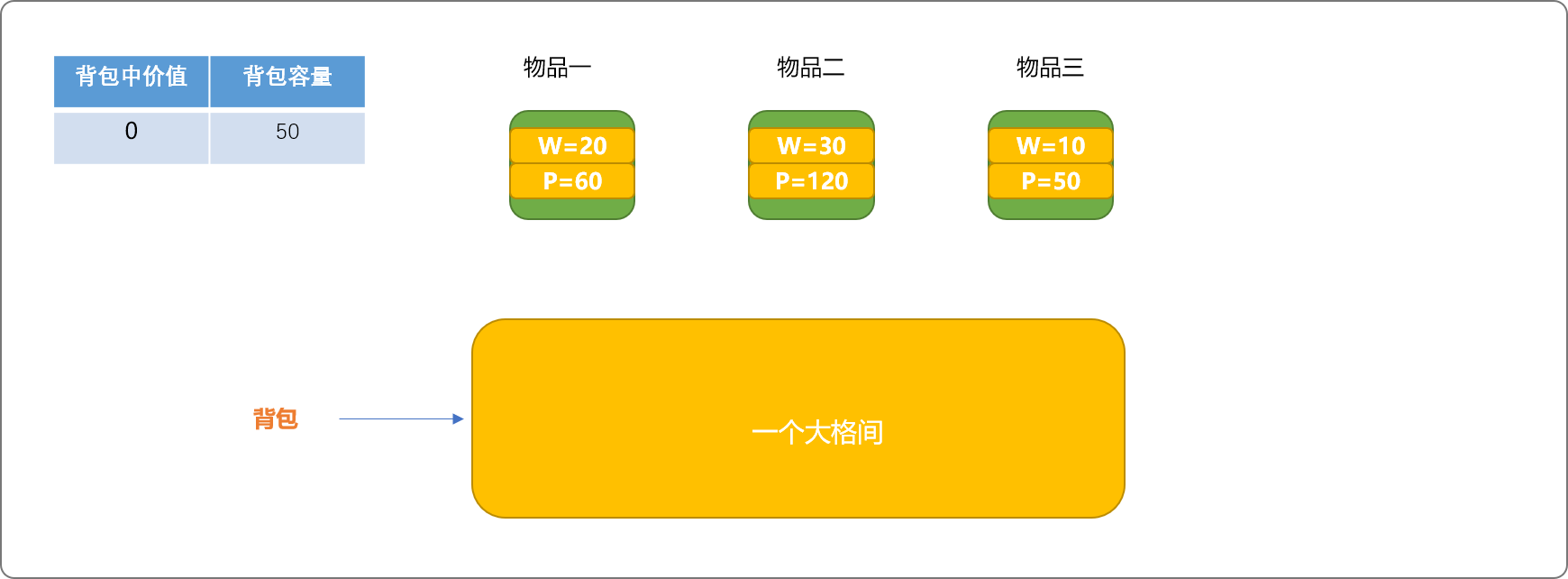
物品放入格间的条件:
- 物品不曾在背包中。
- 物品的重量小于或等于背包现有容量。
如下图,把物品一放入背包中。且把背包剩下空间想象为一个格间,在余下的物品中选择一个放入此格间中。
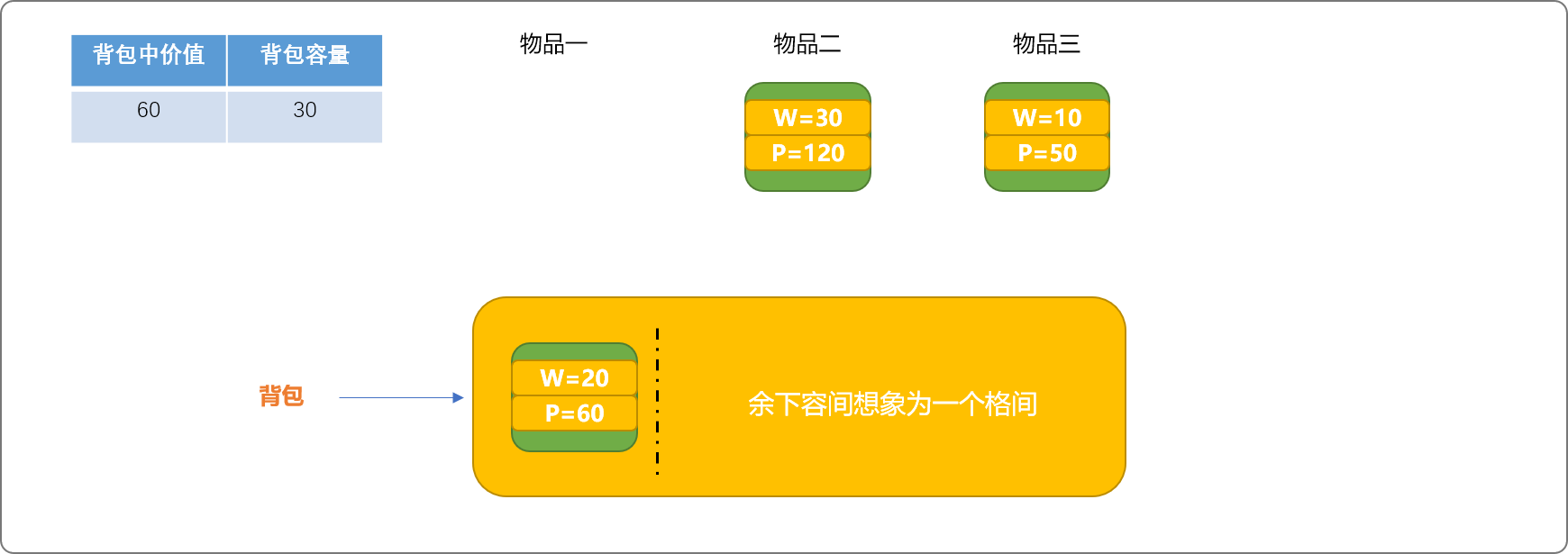
如下,把物品二放入格间中。
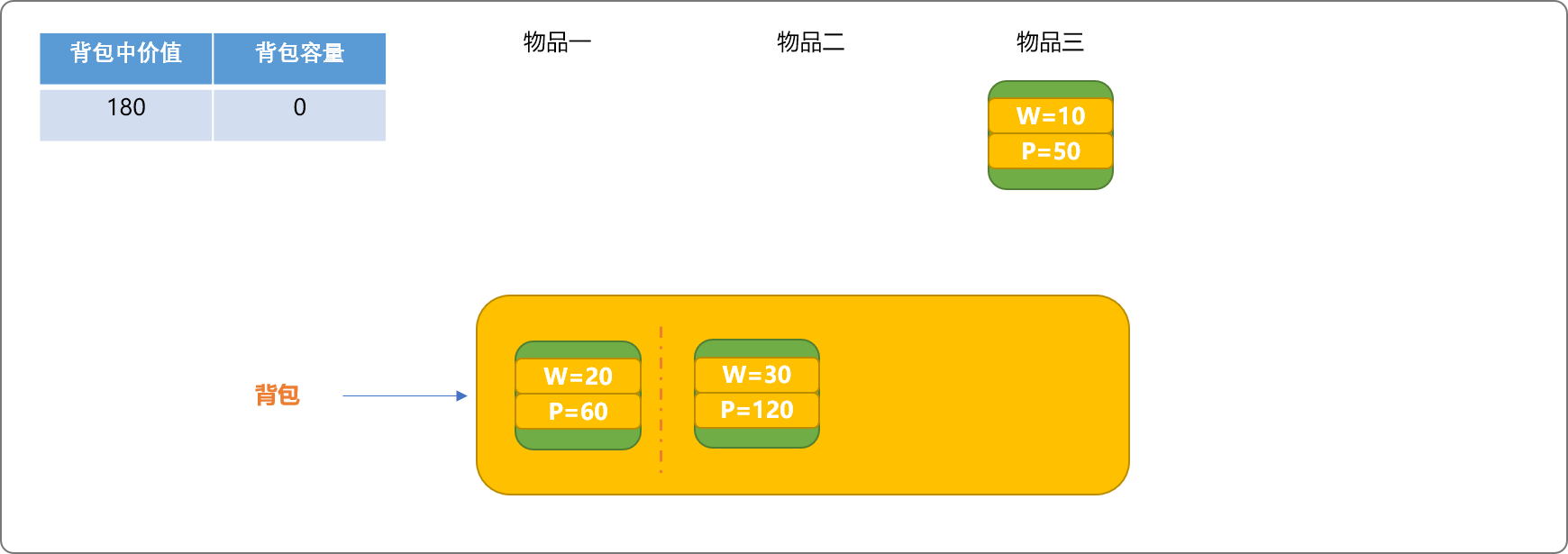
因物品一和物品二的重量之和为 50。等于背包总容量。此时,背包中已经没有剩余空间。也意味着不能再向此背包中放入物品。
至此,可以输出背包中的物品,且把背包中的总价值 180 存储在全局变量中,以便在后续操作时,查找是否还有比此值更大的值。
回溯物品
所谓回溯物品,指把物品从背包中移走,试着再放入一个其它物品。
如下图,回溯物品二,腾出格间。因物品三满足放入条件,放入格间。
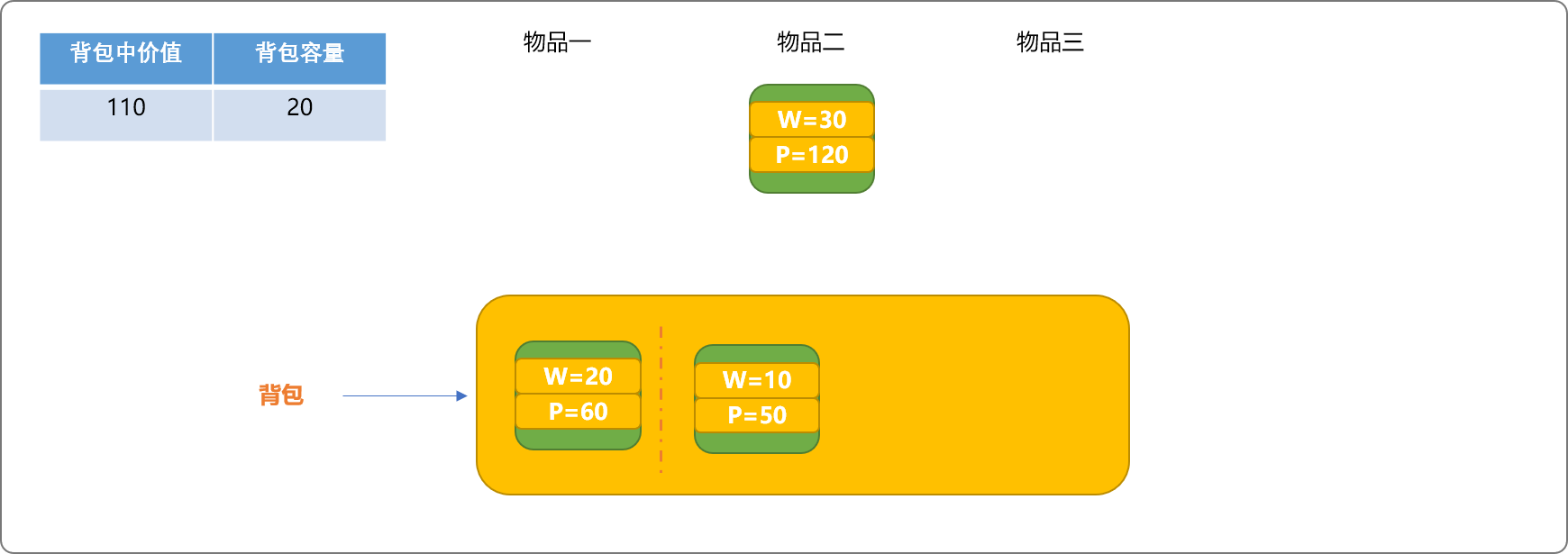
此时,背包还有剩余空间,同样把剩余空间想象成一个格间。因有剩余空间,可以试着把物品二放入背包中。
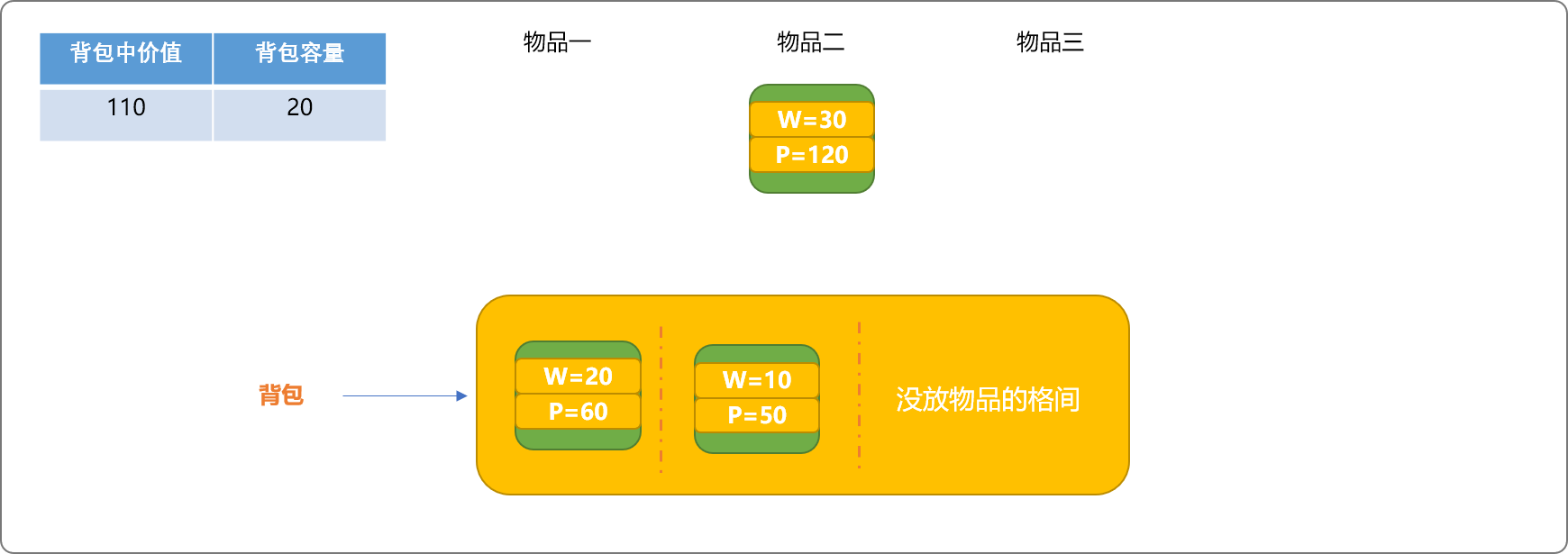
但因物品二的重量大于背包已有的容量,不能放入。此时,可以输出背包中的物品信息,并记录背包中的最大价值为110。因比前面的180的值小,继续保留 180这个价值为当前最大值。
对上述流程做一个简单总结:
-
当背包还有空间,且有物品可以放入时,则加入到背包中。
-
当背包不再能放下任何一件物品时,计算此时的总价值,并确定是不是最大价值。
Tips:这里有一点需要注意,递归函数的出口有
2个,一是还有物品可选择,但不能放入背包中。二是不再有物品可供选择。 -
回溯当前已经放入物品,选择其它物品,重复上述过程,一直到找到真正的最大值。
代码如下所示:
#include<bits/stdc++.h>
using namespace std;
struct Goods {//重量int weight;//价值int price;//装入状态bool isUse;
};
/*
*初始化
*/
Goods allGoods[3]= { {20,60,false},{30,120,false},{10,50,false}};//背包重量
int weight=50;
//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
/*
* 0-1 背包
* idx:物品编号,只需要考虑组合
* deep:递归深度
*/
void bag(int idx,int deep,int weight) {//每次都可以从所有物品中进行选择for(int i=idx; i<3; i++) {if( allGoods[i].isUse==false ) {//物品不曾放入背包if( allGoods[i].weight<=weight) {//且可以放下,增加背包中的总价值totalPrice+=allGoods[i].price;//标志此物品已经放入allGoods[i].isUse=true;//继续放置物品bag(i,deep+1,weight - allGoods[i].weight);//回溯totalPrice-=allGoods[i].price;allGoods[i].isUse=false;} else {//出口一:不可以放下,计算此时背包中的物品的价值是否是最大值,cout<<"-----------查询到某个物品不能放下时,显示背包中信息------------"<<endl;if(totalPrice>maxPrice) maxPrice= totalPrice;for(int j=0; j<3; j++)if(allGoods[j].isUse)cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;return ;}}}//出口二:不再有物品可以选择cout<<"--------当没有物品可选择时也要显示背包中物品信息-----------"<<endl;if(totalPrice>maxPrice) maxPrice= totalPrice;cout<<"此时背包中物品"<<endl;for(int j=0; j<3; j++)if(allGoods[j].isUse)cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;
}
//测试
int main() {bag(0,1,weight);cout<<"---------------------"<<endl;cout<<"最终背包中最大价值"<<maxPrice<<endl;return 0;
}
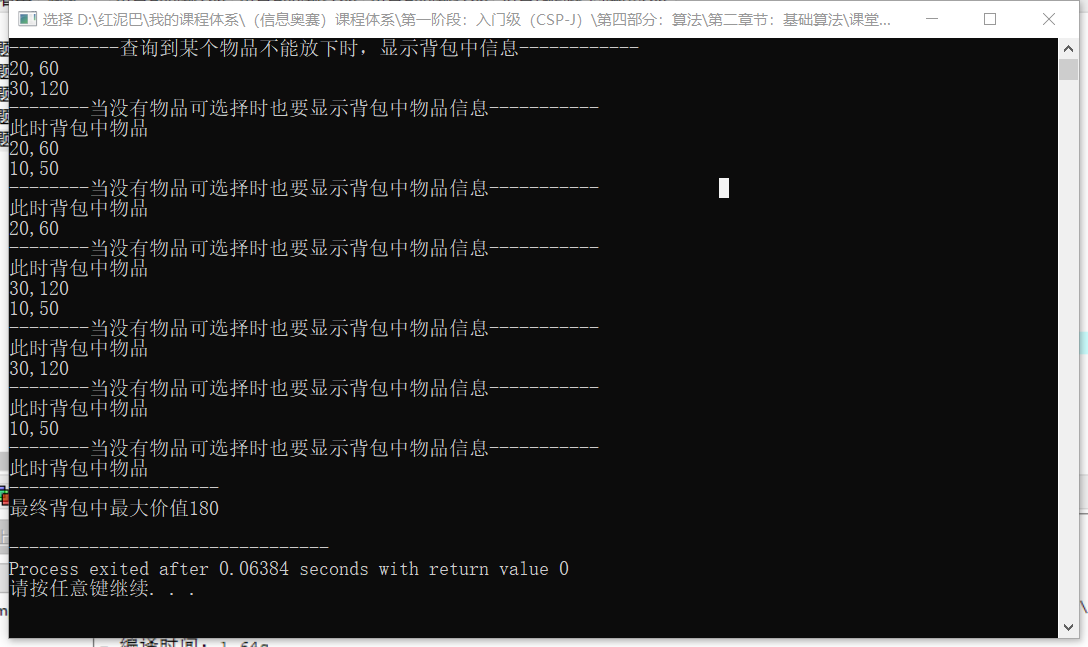
测试结果:
2.1.2 第二种回溯方案
第一种回溯方案,略显复杂,可以采用下面的回溯方案。
此方案中把物品可放入和不可放入做为选择。但其本质和上述实现是一样的。
#include<bits/stdc++.h>
using namespace std;
struct Goods {//物品重量int weight;//物品价值int value;//物品状态 1 已经使用,0 未使用int isUse;
};//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
//背包重量
int bagWeight=100;
//物品信息
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
int count=4;
/*
*显示背包中物品
*/
void showBag() {for(int i=0; i<5; i++) {if(allGoods[i].isUse)cout<<allGoods[i].weight<<","<<allGoods[i].value<<endl;}
}
/*
* idx: 物品编号
* count: 物品总数量
*/
void zeroAndOneBag(int idx,int weight) {//物品只有两种状态for(int i=0; i<=1; i++) {if( weight-allGoods[idx].weight*i>=0 ) {//物品状态allGoods[idx].isUse=i;//总价值totalPrice+=allGoods[idx].value*i;if(idx==4) {if(totalPrice>maxPrice) {maxPrice=totalPrice;cout<<"------------"<<endl;showBag();cout<<maxPrice<<endl;}} else {zeroAndOneBag(idx+1,weight-allGoods[idx].weight*i);}//回溯allGoods[idx].isUse=0;totalPrice-=allGoods[idx].value*i;}}
}
//测试
int main() {zeroAndOneBag(0,bagWeight);return 0;
}
2.1.3 第三种方案
前两种方案,不仅可得到最优值,且可以得到寻找过程中的各种组合方案。如果仅仅是想得到最终结果,不在乎中间的过程,则可以使用下面的递归方案。
#include<iostream>
#include<windows.h>//max函数
using namespace std;
struct Goods {//重量int weight;//价值int price;//装入状态bool isUse;
};
//所有物品
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
//背包重量
int bagWeight = 100;
//物品总数量
int totalNumber = 5;
/*
*递归
*/
int zeroAndOneBag(int index, int remainWeight) {int totalPrice = 0;//没有物品可放if (index == totalNumber) return 0;if (allGoods[index].weight > remainWeight)//当前物品不能放入,查看其它物品放入的情况totalPrice = zeroAndOneBag(index + 1, remainWeight);else//当前物品可以放入,则在把此物品放入和不放入背包时的最大价值 totalPrice = max(zeroAndOneBag(index + 1, remainWeight -allGoods[index].weight) + allGoods[index].price, zeroAndOneBag(index + 1, remainWeight));return totalPrice;
}
//测试
int main() {int value = zeroAndOneBag(0, bagWeight);cout << value << endl;return 0;
}
2.2 动态规划
背包问题,有 2 个状态值,背包的容量和可选择的物品。
- 物品对于背包而言,只有
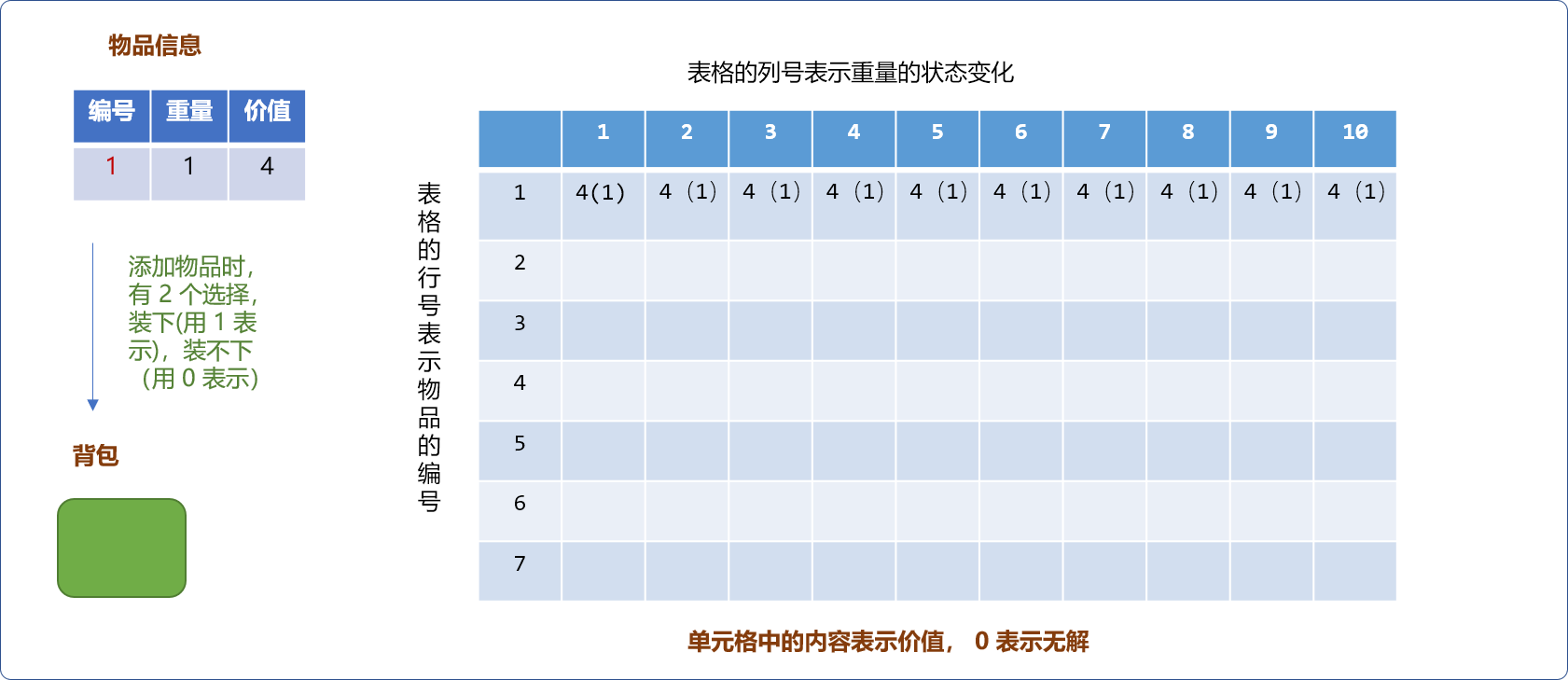
2种选择,要么装下物品,要么装不下,如下图所示,表格的行号表示物品编号,列号表示背包的重量。单元格中的数字表示背包中最大价值。当物品只有一件时,当物品重量大于背包容量,不能装下,反之,能装下。如下图,物品重量为1。无论何种规格容量的背包都能装下(假设背包的容量至少为1)。
- 如下图,当增加重量为
2的物品后,当背包的容量为1时,不能装下物品,则最大值为同容量背包中已经有的最大值。
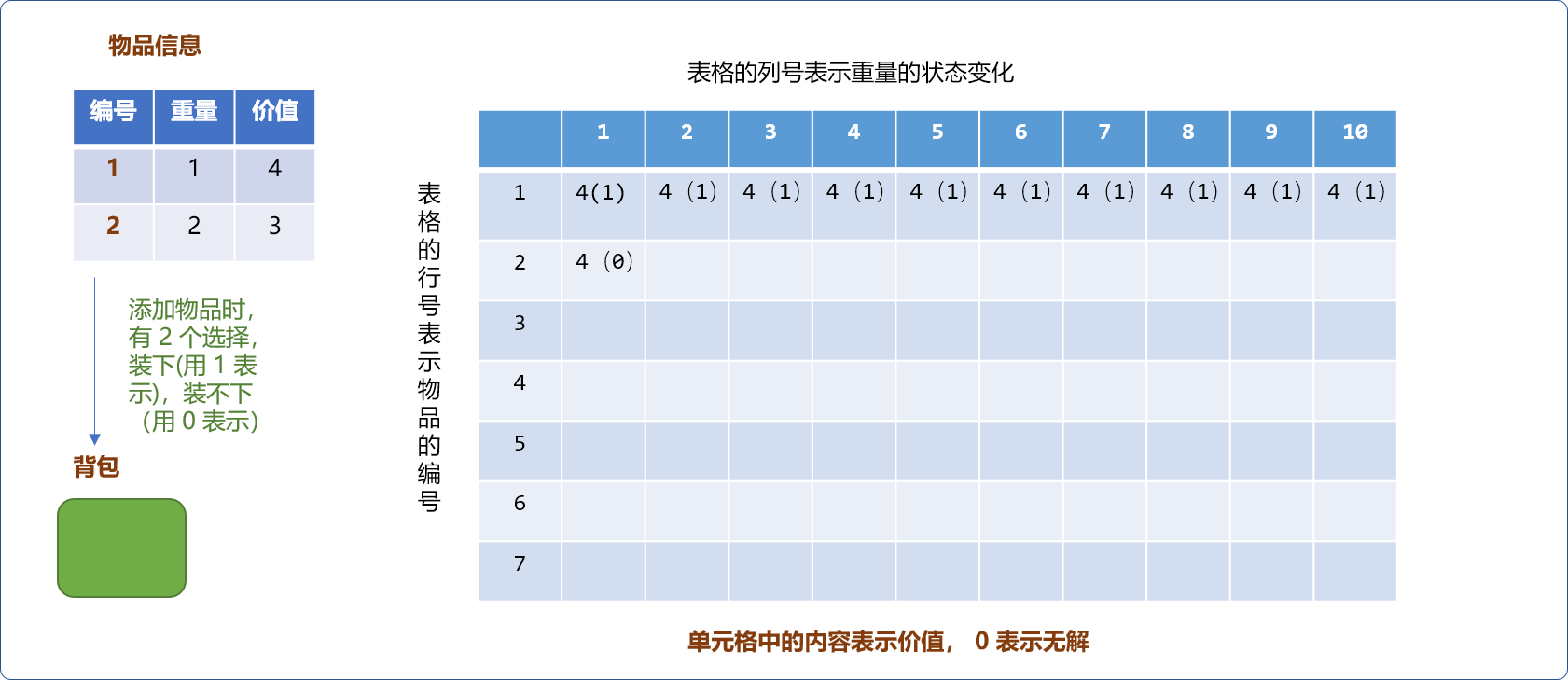
但对容量为 2的背包而言,恰好可以放入新物品,此时背包中的最大价值就会有 2 个选择,一是把物品 2 放进去,背包中的价值为 3。二是保留背包已有的价值4。然后,在两者中选择最大值 4。
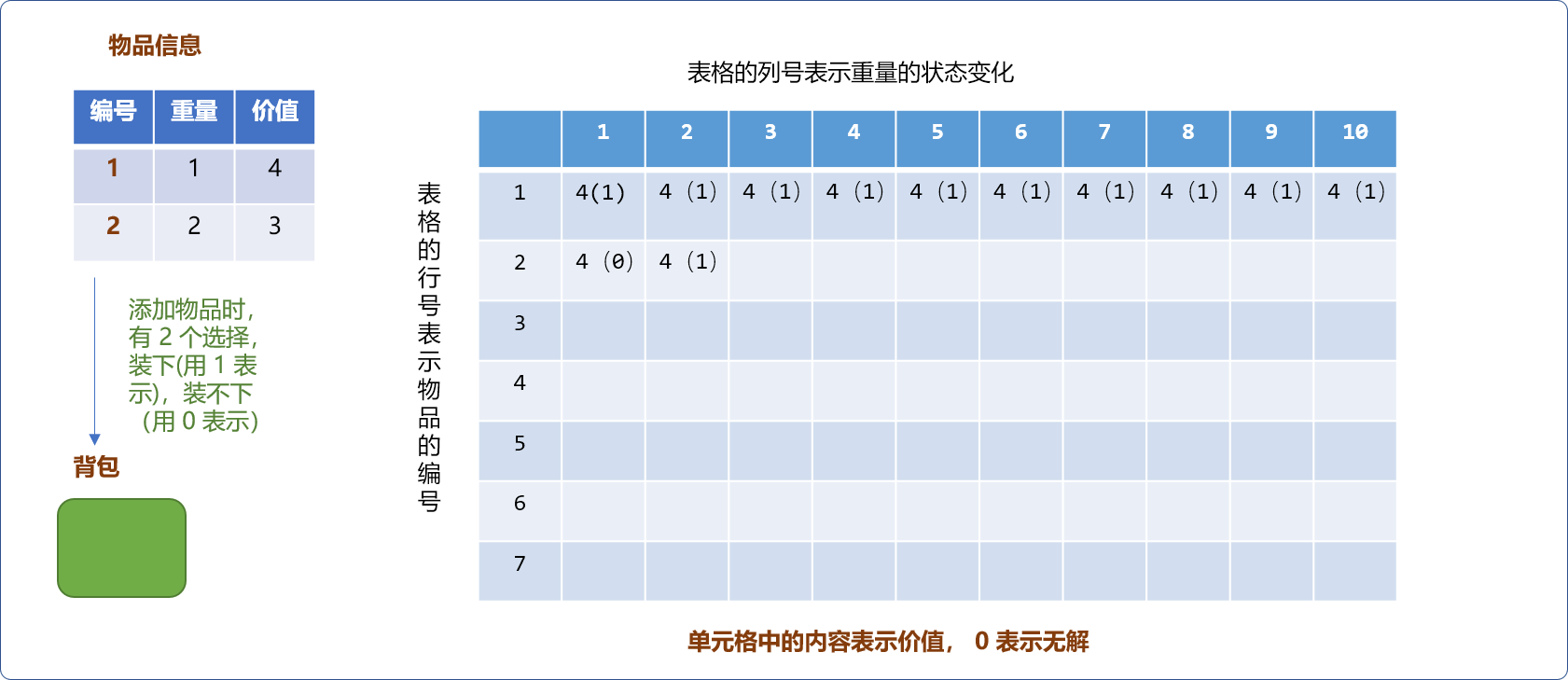
当背包容量是 3时,物品2也是可以放进去的。此时背包的价值可以是当前物品的价值 3加上背包剩余容量3-2=1能存放的最大价值4,计算后值为 7。要把此值和不把物品放进去时原来的价值 4 之间进行最大值选择。
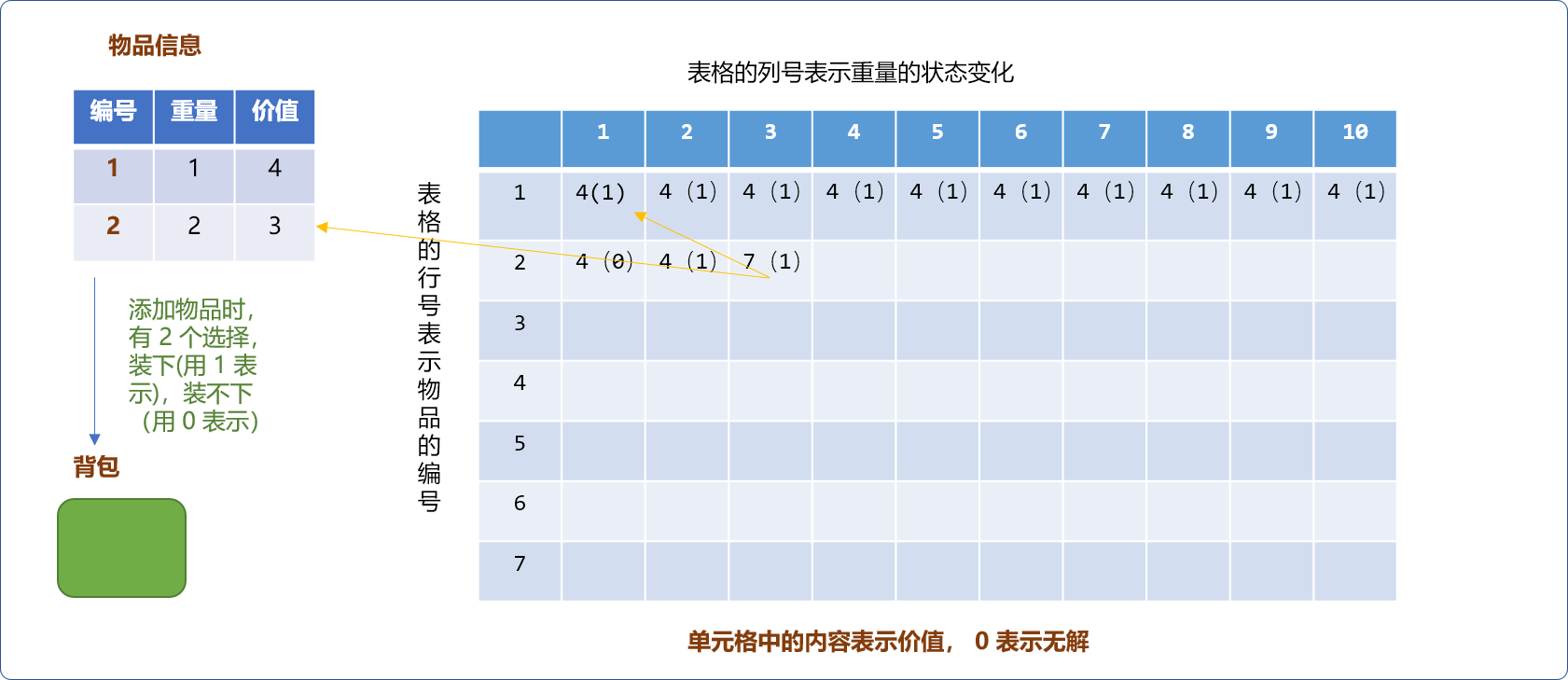
所以,对于背包问题,核心思想就是:
- 如果物品能放进背包:则先计算出物品的价值加上剩余容量能存储的最大价值之和,再找到不把物品放进背包时背包中原有价值。最后在两者之间进行最大值选择。
- 当物品不能放进背包:显然,保留背包中原来的最大价值信息。
2.3.3 编码实现
#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char** argv) {//物品信息int goods[3][3]= { {1,4},{2,3} };//背包容量int bagWeight=0;cout<<"请输入背包容量:"<<endl;cin>>bagWeight;//状态表int db[4][bagWeight+1]= {0};for(int i=0; i<4; i++) {for(int j=0; j<bagWeight+1; j++) {db[i][j]=0;}}for(int w=1; w<4; w++) {for(int wt=1; wt<=bagWeight; wt++) {if( goods[w-1][0]>wt ) {//如果背包不能装下物品,保留背包上一次的结果db[w][wt]=db[w-1][wt];} else {//能装下,计算本物品价值和剩余容量的最大价值int val=goods[w-1][1] + db[w-1][ wt- goods[w-1][0] ];//背包原来的价值int val_= db[w-1][wt];//计算最大值db[w][wt]=val>val_?val:val_;}}}for(int i=1; i<3; i++) {for(int j=1; j<=bagWeight; j++) {cout<<db[i][j]<<"\t";}cout<<endl;}return 0;
}
输出结果:
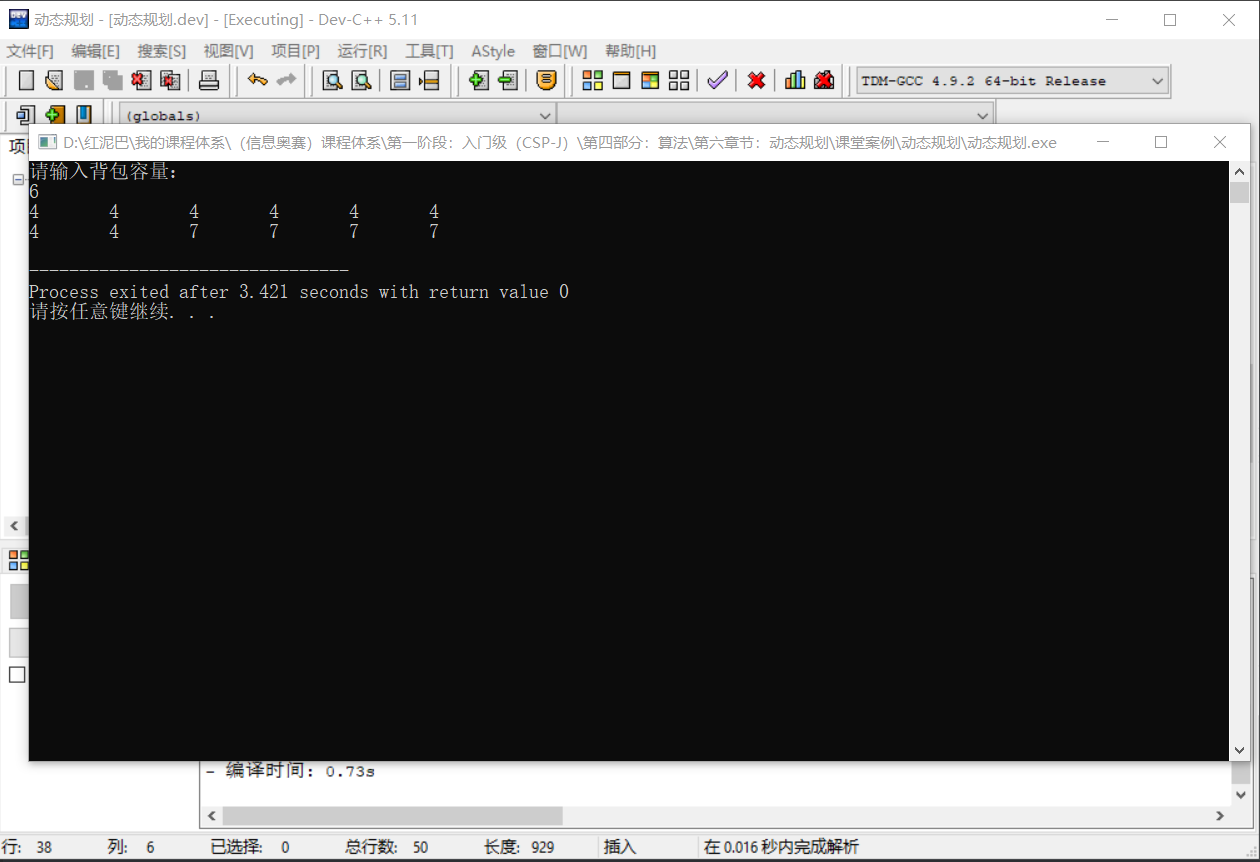
3. 总结
本文主要讲解背包系列 中的0-1背包问题。0-1背包问题可以使用递归和动态规划方案得到其解。
相关文章:

C++ 算法主题系列之集结0-1背包问题的所有求解方案
1. 前言 背包问题是类型问题,通过对这一类型问题的理解和掌握,从而可以归纳出求解此类问题的思路和模板。 背包问题的分类有: 0-1背包问题,也称为不可分割背包问题。无限背包问题。判定性背包问题.带附属关系的背包问题。双背包…...

【Vue】Vue常见的6种指令
Vue的6种指令-前言指令(Directives)是vue 为开发者提供的模板语法,用于辅助开发者渲染页面的基本结构。vue 中的指令按照不同的用途可以分为如下6 大类① 内容渲染指令 ② 属性绑定指令 ③ 事件绑定指令 ④ 双向绑定指令 ⑤ 条件渲染指令 ⑥ …...
四年学习资料_文件目录树)
计算机科学与技术(嵌入式)四年学习资料_文件目录树
说明: 资料内容主要包括:计嵌专业2019级大学四年主要科目的各种电子资料,有电子实验报告、课程设计报告、课程设计项目、整理复习笔记、电子书、ppt、练习题、期末试卷、部分课程软件资源、科创项目,职业生涯规划书,大…...
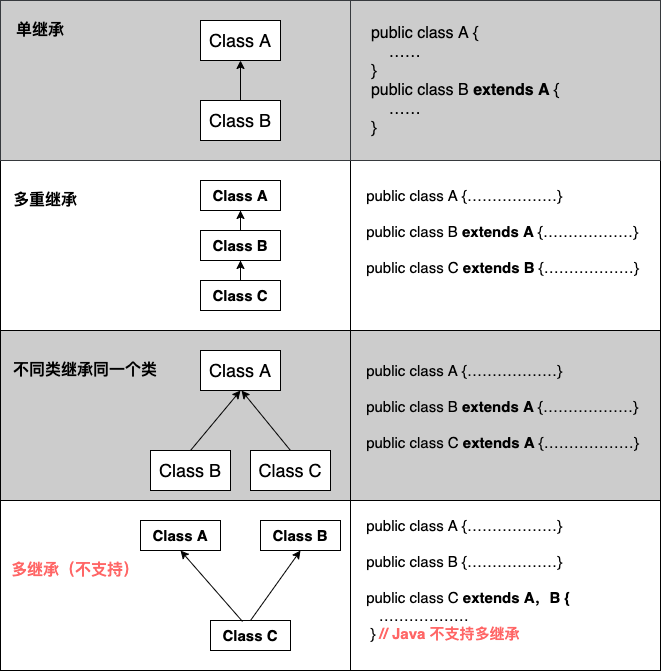
【java】Java 继承
文章目录继承的概念生活中的继承:类的继承格式为什么需要继承公共父类:继承类型继承的特性继承关键字extends关键字implements关键字super 与 this 关键字final 关键字构造器继承的概念 继承是java面向对象编程技术的一块基石,因为它允许创建…...

自媒体账号数据分析从何入手?
账号的数据可以直接反应这个账号的好坏,数据越高收益就会越好,数据越差收益自然高不了。 新手要从哪些方面入手见效更快呢?今天大周就来把自己的经验分享给粉丝们! 1、账号定位 (1)账号所创作的领域 &a…...

Clickhouse新版本JSON字段数据写入方式
Clickhouse新版本JSON字段数据写入方式 在Clickhouse版本22.3.1版本以上,提供了针对JSON格式数据的新的数据类型:JSON,从而实现了存储此类数据由原先的结构化表结构,更新为现在的半结构化表存储。对于新增字段,某些同…...

HNU-电路与电子学-实验2
实验二 模型机组合部件的实现(一) 班级 计XXXXX 姓名 wolf 学号 2021080XXXXX 一、实验目的 1.了解简易模型机的内部结构和工作原理。 2.熟悉译码器、运算器的工作原理。 3.分析模型机的功…...
从0开始学python -49
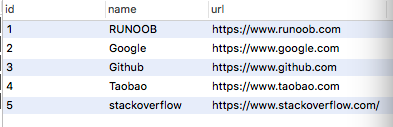
Python MySQL - mysql-connector 驱动 -2 插入数据 插入数据使用 “INSERT INTO” 语句: demo_mysql_test.py: 向 sites 表插入一条记录。 import mysql.connectormydb mysql.connector.connect(host"localhost",user"root",passwd"…...

Spring MVC 详解(连接、获取参数、返回数据)
在之前我们先简单那谈谈Spring、SpringBoot以及Spring MVC框架之间有什么关系?首先Spring是一个框架,SpringBoot脚手架是为了快速开发Spring框架而创造的技术。可以理解为SpringBoot又在Spring上面包了一层壳子,是基于Spring的,是…...
IT女神节(致敬中国IT界永远的女神严蔚敏-数据结构)
我们都知道程序数据结构算法。相信很多人都学过严蔚敏的数据结构的课程。作为一个码农,在这不管是3.7女神节,还是3.8妇女节。我觉得都有必要向这些教育界的老前辈致敬。今天我就梳理梳理,最经典的数据结构教材。 严蔚敏介绍(来自…...

Java 集合分页
一、前言 在Java开发中,若单次展示的数据量太大,会造成程序响应缓慢,就需要用到 分页 功能,每一页展示一定量的数据,分多次展示 ... 那么在List集合中,如何实现 分页 功能呢? 本文将以3种方式&a…...

代码随想录之哈希表(力扣题号)
242. 有效的字母异位词 直接用数组模拟哈希表 只有小写字母,开26的数组就可以了 class Solution {public boolean isAnagram(String s, String t) {//24-28int[] hash new int[26];Arrays.fill(hash,0);for(int i0;i<s.length();i){hash[s.charAt(i)-a];}for(i…...
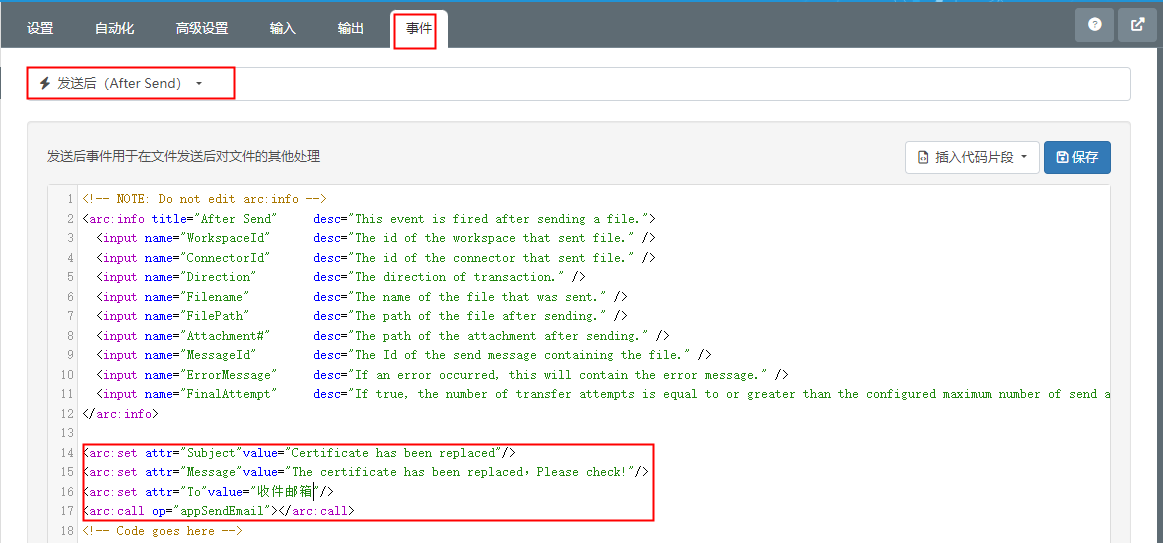
如何在知行之桥EDI系统中定时自动更换交易伙伴AS2证书?
为了保证客户与交易伙伴之间数据传输的安全性,AS2传输协议中,通常会通过一对数字证书对传输数据进行签名和加密。但是证书是有有效期的,在证书到期之前,需要贸易双方及时更换新的证书。 在更新证书时,由于客户通常是和…...

辽宁千圣文化:抖音店铺怎么做二次优化?
抖音商品卡订单是指永华在抖音、抖音极速版,通过直播的方式出现短视频页面商品卡之后,直接成交商品详情页直接成交后的订单,那么跟着辽宁千圣文化小编来一起看看吧!一.与政策有关1.什么是「商品卡订单」?用户通过抖音、…...

检测js代码中可能导致内存泄漏的工具
JavaScript 中闭包等问题可能导致内存泄漏,因为闭包中引用的变量不会被垃圾回收器自动释放。以下是一些可以用来检测 JavaScript 代码中可能导致内存泄漏的工具: 1、Chrome 开发者工具 Chrome 开发者工具中有一个 Heap Profiler 工具,可以帮…...

linux和centos读写日期到文件并对日期进行比较
#!/bin/bash adate -d "${a}" %s #必须用数字 %s是取时间戳秒数 ddate -d "${c}" %s echo m$(($a - $d)) #必须2个小括号 a1date %s echo $a1 sleep 2 b1date %s echo $(($a1 - $b1)) #必须2个小括号 if [ $a1 -eq $b1 ];then #必须有空格 echo "…...

Espressif-IDE v2.8.0 新增功能及开发方向
在乐鑫最近发布的 Espressif-IDE 2.8.0 版本中,我们推出了分区表编辑器和 NVS 分区编辑器功能,优化现有调试器的配置功能并修复多项 Bug ,进一步为用户提升了插件质量以及稳定性。 用户可以点此获取最新版本。 • 若您的设备为 Windows 系统…...

C++学习笔记之基础
目录前言一.零碎知识点二.C核心2.1.内存分区2.2.引用2.3.函数2.4.类和对象2.4.1.对象的初始化和清理2.4.2.构造函数和析构函数2.4.3.构造函数的分类和调用2.4.4.拷贝构造函数的调用时机2.4.5.深拷贝与浅拷贝2.4.6.初始化列表2.4.7.类对象作为类的成员2.4.8.静态成员2.4.9.C对象…...
)
博弈论小课堂:零和博弈(找到双方的平衡点)
文章目录 引言I 零和博弈1.1 零和博弈的策略1.2 博弈类型1.3 找到平衡点(equilibrium)II 多人博弈的投篮问题2.1 比赛规则2.2 零和博弈的计算引言 从概率论延伸出来的课题——博弈论,博弈论中最典型的两大类博弈,是“零和博弈”与“非零和博弈”。博弈论所研究的最优化问题…...
)
Redisson 分布式锁(基于v1.3.1)
Redisson 分布式锁 v1.0.0版本问题 v1.0.0版本的实现在持有锁的JVM或者持有锁的线程挂掉没有释放锁时,该锁不会被释放并且会一直占用,这个时候就使用DEL命令手动删除。 问题解决 v1.3.1版本通过key的ttl解决了这个问题,关键加锁逻辑改为了…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
