[蓝桥杯 2018 省 A] 付账问题
【蓝桥杯】付账问题
[蓝桥杯 2018 省 A] 付账问题
题目描述
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。
现在有 n n n 个人出去吃饭,他们总共消费了 S S S 元。其中第 i i i 个人带了 a i a_i ai 元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?
为了公平起见,我们希望在总付钱量恰好为 S S S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 1 1 分钱的整数倍。你需要输出最小的标准差是多少。
标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的“偏差有多大”。形式化地说,设第 i i i 个人付的钱为 b i b_i bi 元,那么标准差为 s = 1 n ∑ i = 1 n ( b i − 1 n ∑ i = 1 n b i ) s=\sqrt{\frac{1}{n}\sum_{i=1}^n(b_i-\frac{1}{n}\sum_{i=1}^n b_i)} s=n1∑i=1n(bi−n1∑i=1nbi)
输入格式
第一行包含两个整数 n n n、 S S S;
第二行包含 n n n 个非负整数 a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an。
输出格式
输出到标准输出。
输出最小的标准差,四舍五入保留 4 4 4 位小数。
保证正确答案在加上或减去 1 0 − 9 10^{-9} 10−9 后不会导致四舍五入的结果发生变化。
样例 #1
样例输入 #1
5 2333
666 666 666 666 666
样例输出 #1
0.0000
样例 #2
样例输入 #2
10 30
2 1 4 7 4 8 3 6 4 7
样例输出 #2
0.7928
提示
【样例解释】
- 每个人都出 2333/5 元,标准差为 0。
【数据约定】
对于 10 % 10\% 10% 的数据,所有 a i a_i ai 相等;
对于 30 % 30\% 30% 的数据,所有非 0 0 0 的 a i a_i ai 相等;
对于 60 % 60\% 60% 的数据, n ≤ 1000 n \le 1000 n≤1000;
对于 80 % 80\% 80% 的数据, n ≤ 1 0 5 n \le 10^5 n≤105;
对于所有数据, n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 9 n \le 5 \times 10^5,0 \le a_i \le 10^9 n≤5×105,0≤ai≤109。
标签:贪心
思路:
标准差,即数据的分散程度,分散度高标准差大,反之则越小。
我们使标准差小,则尽可能让数据集中在平均数附近
$ a_i<avg(平均数) , 则 ,则 ,则b_i=a_i$ a v g − a i avg-a_i avg−ai为不够的钱,由钱多的均摊
有5个人带的钱为 a 1 , a 2 , a 3 , a 4 , a 5 a_1,a_2,a_3,a_4,a_5 a1,a2,a3,a4,a5,avg为每个人付款的平均数,总付款sum
a 1 a1 a1小于 a v g avg avg,因此他只能付 a 1 a1 a1,多的钱 a v g − a 1 avg-a1 avg−a1由 a 2 到 a 5 a_2到a_5 a2到a5来均摊,
即付款c = s u m − a 1 / ( n − 1 ) =sum-a1/(n-1) =sum−a1/(n−1),如果 c > a 2 c>a2 c>a2,同样 a 2 a2 a2拿出所有的钱,剩下的由后面的均摊,以此类推
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
long double money[N];
signed main()
{int n; long double s=0.0;//注意这里,虽然将int定义为long long但输入的是long long 类型时,输入格式一定还是%lld,否则会出错scanf("%lld %Lf",&n,&s);//long double输入输出格式为%Lflong double ave=s/n;//平均数for(int i=0;i<n;i++)scanf("%Lf",&money[i]);sort(money,money+n);long double sum=0,t=0;for(int i=0;i<n;i++)//想让我们的标准差小,每个数尽量集中在平均数附近,先排序,遍历一遍这些数//如果这个数小于平均数,就要拿出全部的值,不够的钱a由钱多于平均数的人去均摊,使后面的人的付钱平均数提高//可能出现因为平均数提高后面的人也拿不出来这么多钱,那我们就让他拿出全部钱,剩下的钱仍由更后面的人去分摊{t=min(s/(n-i),money[i]);//注意min里的参数中数据类型要一致,即int对应int,long double和long double对应sum+=(t-ave)*(t-ave);s-=t;}printf("%.4Lf",sqrt(sum/n));return 0;
}
相关文章:

[蓝桥杯 2018 省 A] 付账问题
【蓝桥杯】付账问题 [蓝桥杯 2018 省 A] 付账问题 题目描述 几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。 现在有 n n n 个人出去吃饭,他们总共消费了 S S S 元。其中第 i i i 个人带了 a i a_i ai 元。幸运的是&#…...
)
设计模式|装饰器模式(Decorator Pattern)
文章目录 结构优缺点优点缺点适用场景示例装饰器模式(Decorator Pattern)是一种结构型设计模式,它允许在不改变原始对象的基础上,动态地给对象添加新的功能或责任。这种模式是通过创建一个包装对象,也就是装饰器,来包裹真实的对象,然后在装饰器中添加新的行为或功能。这…...

发作性睡病有性别差异吗?
发作性睡病是一种特殊的睡眠障碍,以不可控制的嗜睡、猝倒发作、睡眠瘫痪、入睡前幻觉以及夜间睡眠紊乱为主要临床特点。关于发作性睡病是否存在性别差异,不同的研究和报道给出了不同的结论。 一方面,从生理角度来看,男性和女性在…...

ppt从零基础到高手【办公】
第一章:文字排版篇01演示文稿内容基密02文字操作规范03文字排版处理04复习&作业解析第二章:图形图片图表篇05图形化表达06图片艺术化07轻松玩转图表08高效工具&母版统一管理09复习&作业解析10轻松一刻-文字图形小技巧速学第三章:…...

文件上传下载
文章目录 文件上传下载文件上传文件下载 文件上传下载 HTTP请求会包含一个请求头,其中"Content-Type"字段告诉服务器正在发送什么类型的数据。根据发送的数据类型,浏览器和服务器会采取适应的处理方式。 "multipart/form-data"是一…...

C++11 新特性:新增算法
C11 在标准库中引入了一系列新的算法,这些新增的算法使我们的代码写起来更简洁方便。 下面是 C11 中新增加的一些重要算法的简要描述和使用方法: 1、非修改序列操作 std::all_of:检查范围内的所有元素是否都满足指定的谓词。std::any_of&a…...
c/c++普通for循环学习
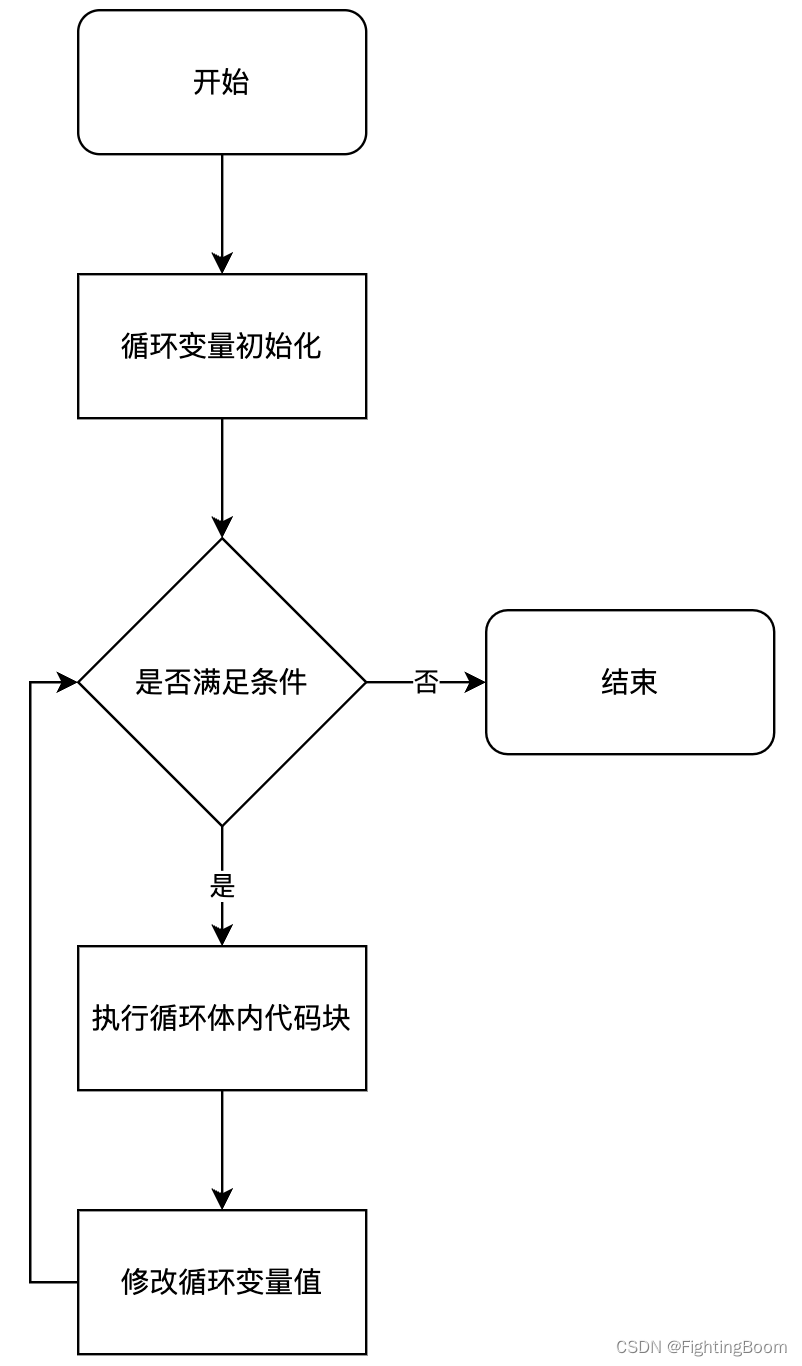
学习一下 for 循环的几种不同方式,了解一下原理及差异 完整的测试代码参考 GitHub :for 循环测试代码 1 常用形态 对于 for 循环来说,最常用的形态如下 for (表达式1; 表达式2; 表达式3) {// code }流程图如下: 编写测试代码…...
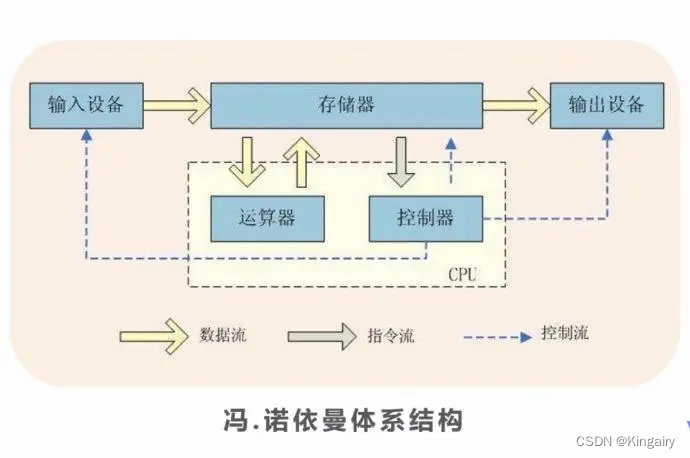
操作系统组成部分
从1946年诞生第一台电子计算机。 冯诺依曼结构 冯诺依曼是:数字计算机的数制采用二进制;计算机应该按照程序顺序执行。 常见的操作系统有三种类型 单用户单任务操作系统:只支持一个用户和一个任务的执行,如DOS;单用…...

深入理解DES算法:原理、实现与应用
title: 深入理解DES算法:原理、实现与应用 date: 2024/4/14 21:30:21 updated: 2024/4/14 21:30:21 tags: DES加密对称加密分组密码密钥管理S盒P盒安全性分析替代算法 DES算法简介 历史 DES(Data Encryption Standard)算法是由IBM研发&…...

# 达梦sql查询 Sql 优化
达梦sql查询 Sql 优化 文章目录 达梦sql查询 Sql 优化注意点测试数据单表查询 Sort 语句优化优化过程 多表关联SORT 优化函数索引的使用 注意点 关于优化过程中工具的选用,推荐使用自带的DM Manage,其它工具在查看执行计划等时候不明确在执行计划中命中…...

Linux下SPI驱动:SPI设备驱动简介
一. 简介 Linux下的SPI 驱动框架和 I2C 很类似,都分为主机控制器驱动和设备驱动,主机控制器也就是 SOC的 SPI 控制器接口,SPI设备驱动也就是所操作的SPI设备的驱动。 本文来学习一下Linux下SPI设备驱动。 二. Linux下SPI驱动:SP…...

【简明图文教程】Node.js的下载、安装、环境配置及测试
文章目录 前言下载Node.js安装Node.js配置Node.js配置环境变量测试后言 前言 本教程适用于小白第一次从零开始进行Node.js的下载、安装、环境配置及测试。 如果你之前已经安装过了Node.js或删除掉了Node.js想重新安装,需要先参考以下博客进行处理后,再根…...

共模电感饱和与哪些参数有关?这些参数是如何影响共模电感的?
在做一个变频器项目,遇到一个问题,在30Hz重载超过一定1小时,CE测试结果超出限制,查找原因最终发现EMI filter内的共模电感加热,fail现象可以复现。最终增大Y电容把问题解决了。由此问题引申出一个问题,到底…...
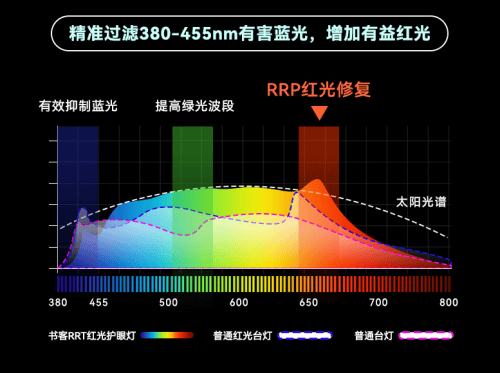
儿童护眼台灯怎么选?五款必选的高口碑护眼台灯推荐
儿童台灯,想必大家都不会陌生了,是一种学生频繁使用的小灯具,一般指放在桌面用的有底座的电灯。随着近年来儿童青少年的视力急速下滑,很多家长都会选择给孩子选择一款合适的护眼台灯,以便孩子夜晚学习能有个好的照明环…...

前端小技巧之轮播图
文章目录 功能htmlcssjavaScript图片 设置了一点小难度,不理解的话,是不能套用的哦!!! (下方的圆圈与图片数量不统一,而且宽度是固定的) 下次写一些直接套用的,不整这些麻…...
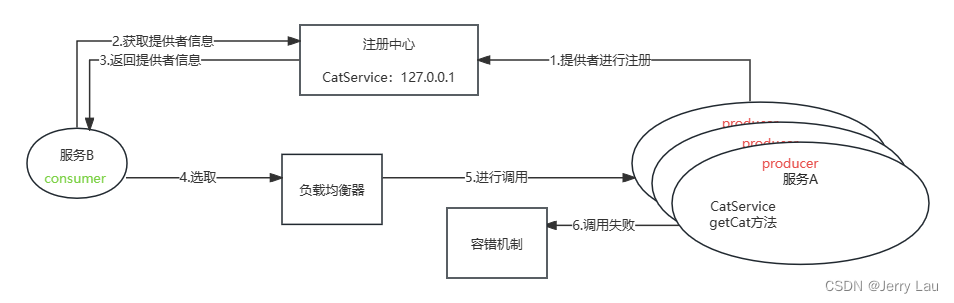
手动实现简易版RPC(上)
手动实现简易版RPC(上) 前言 什么是RPC?它的原理是什么?它有什么特点?如果让你实现一个RPC框架,你会如何是实现?带着这些问题,开始今天的学习。 本文主要介绍RPC概述以及一些关于RPC的知识,为…...
大语言模型总结整理(不定期更新)
《【快捷部署】016_Ollama(CPU only版)》 介绍了如何一键快捷部署Ollama,今天就来看一下受欢迎的模型。 模型简介gemmaGemma是由谷歌及其DeepMind团队开发的一个新的开放模型。参数:2B(1.6GB)、7Bÿ…...
)
关于npm和yarn的使用(自己的问题记录)
目录 一 npm 和 yarn 的区别 二 npm 和 yarn 常用命令对比 1. 初始化项目 2. 安装所有依赖包 3. 安装某个依赖包 4.安装某个版本的依赖包 5. 更新依赖包 5. 移除依赖包 三 package.json中 devDependencies 和 dependencies 的区别。 四 npm安装包时,…...
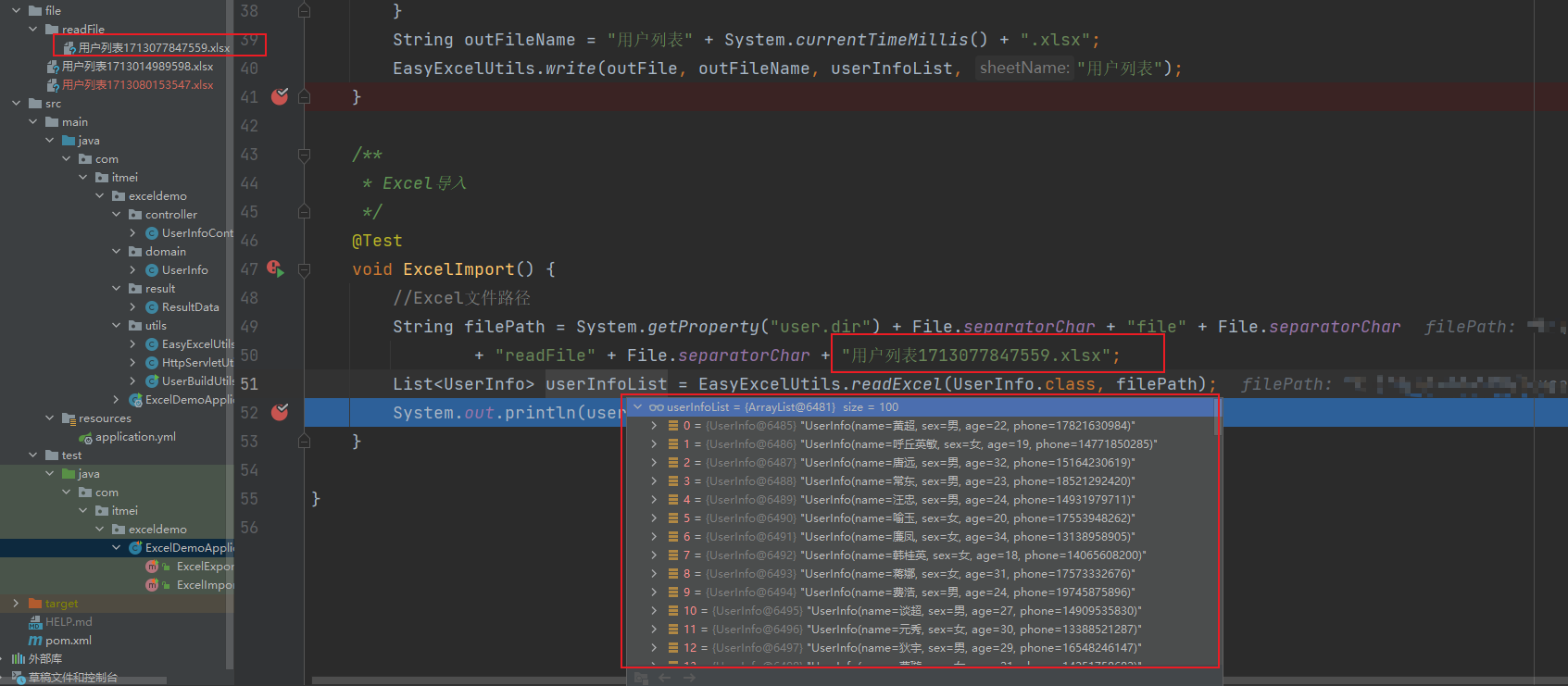
Web端Excel的导入导出Demo
📚目录 📚简介:✨代码的构建:💭Web端接口Excel操作🚀下载接口🚀导入读取数据接口 🏡本地Excel文件操作⚡导出数据🌈导入读取数据 📚简介: 使用阿里巴巴开源组件Easy Exce…...
Java日期正则表达式(附Demo)
目录 前言1. 基本知识2. Demo 前言 对于正则匹配,在项目实战中运用比较广泛 原先写过一版Python相关的:ip和端口号的正则表达式 1. 基本知识 对于日期的正则相对比较简单 以下是一些常见的日期格式及其对应的正则表达式示例: 年-月-日&a…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
