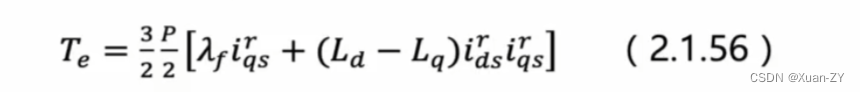【电控笔记5】电流环速度环三环参数整定
相关文章:
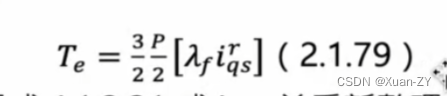
【电控笔记5】电流环速度环三环参数整定
旋转坐标系下的电压方程,由id和iq计算出ud和uq Lq:q轴电感 Ld:d轴电感 输入是电流,输出是电压? 内嵌式pmsm(ipmsm)模型建立: 其中: λf是转子磁场在定子绕组所产生的磁通链,为一常数,在psms中转子磁场非常稳定几乎不变。 ipmsm转矩方程式: 对永磁同步马达而言,使…...

AI克隆语音(基于GPT-SoVITS)
概述 使用GPT-SoVITS训练声音模型,实现文本转语音功能。可以模拟出语气,语速。如果数据质量足够高,可以达到非常相似的结果。相比于So-VITS-SVC需要的显卡配置更低,数据集更小(我的笔记本NVIDIA GeForce RTX 4050 Lap…...

小蚕爬树问题
小蚕爬树问题 问题描述: 编写一个函数 int day(int k,int m,int n),其功能是:返回小蚕需要多少天才能爬到树顶(树高 k 厘米,小蚕每天白天向上爬 m 厘米,每天晚上下滑 n 厘米,爬到树顶后不再下滑࿰…...
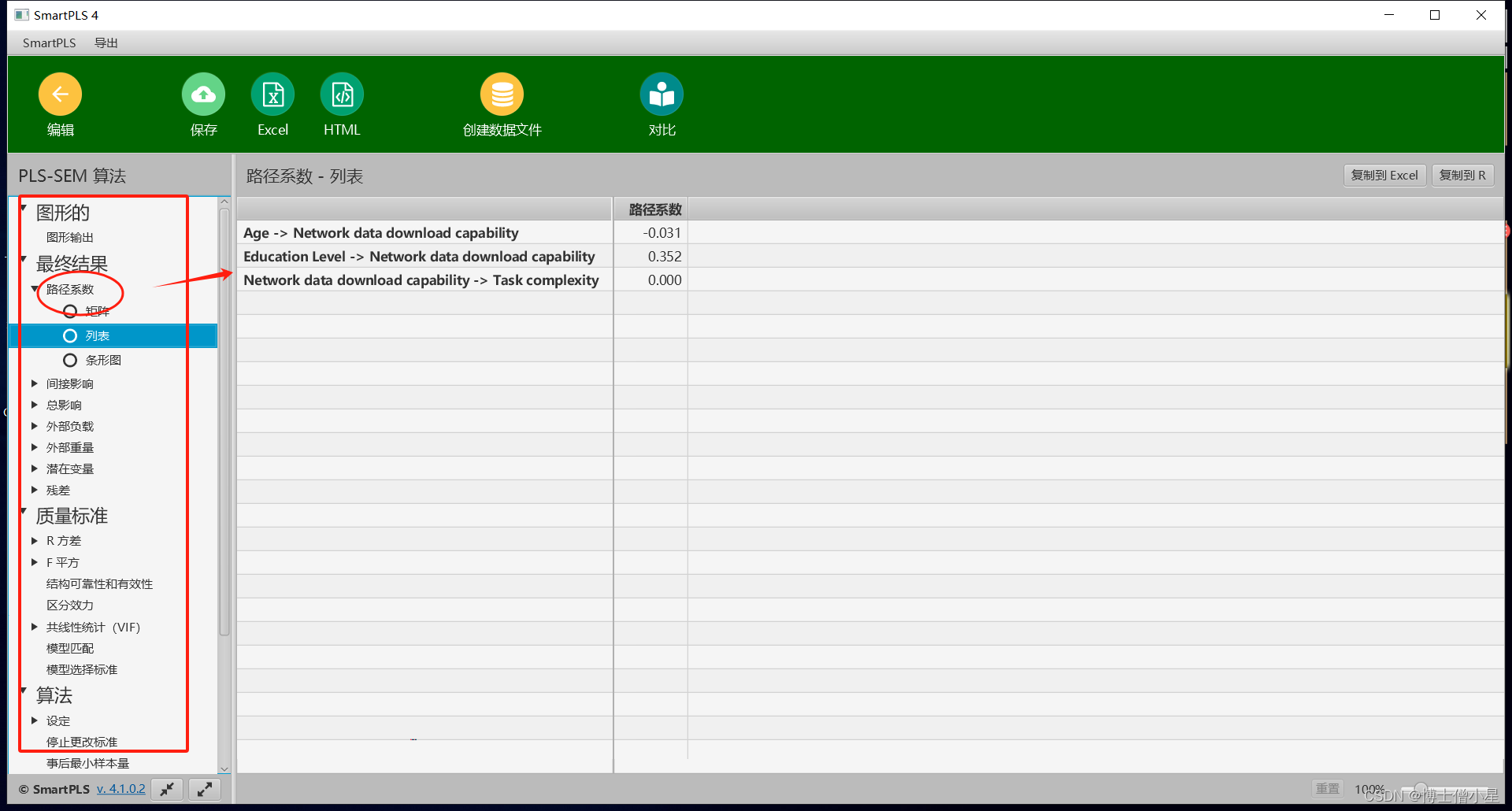
科研学习|科研软件——如何使用SmartPLS软件进行结构方程建模
SmartPLS是一种用于结构方程建模(SEM)的软件,它可以用于定量研究,尤其是在商业和社会科学领域中,如市场研究、管理研究、心理学研究等。 一、准备数据 在使用SmartPLS之前,您需要准备一个符合要求的数据集。…...
实用工具系列-ADB使用方式
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(WPS二次开发QQ群:250325397),摸鱼吹牛嗨起来࿰…...

计算机网络书籍--《网络是怎样连接的》阅读笔记
第一章 浏览器生成信息 1.1 生成HTTP请求信息 1.1.1 URL Uniform Resource Locator, 统一资源定位符。就是网址。 不同的URL能够用来判断使用哪种功能来访问相应的数据,比如访问Web服务器就要用”http:”,而访问FTP服务器用”ftp:”。 FTPÿ…...

antd+vue——datepicker日期控件——禁用日期功能
需求:今天之前的日期禁用 <a-date-pickerv-model.trim"formNE.deliveryTime":disabled-date"disabledDate"valueFormat"YYYY-MM-DD"allowClearstyle"width: 100%" />禁用日期的范围: //时间范围 disab…...

技术分享 | Appium 用例录制
下载及安装 下载地址: github.com/appium/appi… 下载对应系统的 Appium 版本,安装完成之后,点击 “Start Server”,就启动了 Appium Server。 在启动成功页面点击右上角的放大镜,进入到创建 Session 页面。配置好…...

[蓝桥杯 2018 省 A] 付账问题
【蓝桥杯】付账问题 [蓝桥杯 2018 省 A] 付账问题 题目描述 几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。 现在有 n n n 个人出去吃饭,他们总共消费了 S S S 元。其中第 i i i 个人带了 a i a_i ai 元。幸运的是&#…...
)
设计模式|装饰器模式(Decorator Pattern)
文章目录 结构优缺点优点缺点适用场景示例装饰器模式(Decorator Pattern)是一种结构型设计模式,它允许在不改变原始对象的基础上,动态地给对象添加新的功能或责任。这种模式是通过创建一个包装对象,也就是装饰器,来包裹真实的对象,然后在装饰器中添加新的行为或功能。这…...

发作性睡病有性别差异吗?
发作性睡病是一种特殊的睡眠障碍,以不可控制的嗜睡、猝倒发作、睡眠瘫痪、入睡前幻觉以及夜间睡眠紊乱为主要临床特点。关于发作性睡病是否存在性别差异,不同的研究和报道给出了不同的结论。 一方面,从生理角度来看,男性和女性在…...

ppt从零基础到高手【办公】
第一章:文字排版篇01演示文稿内容基密02文字操作规范03文字排版处理04复习&作业解析第二章:图形图片图表篇05图形化表达06图片艺术化07轻松玩转图表08高效工具&母版统一管理09复习&作业解析10轻松一刻-文字图形小技巧速学第三章:…...

文件上传下载
文章目录 文件上传下载文件上传文件下载 文件上传下载 HTTP请求会包含一个请求头,其中"Content-Type"字段告诉服务器正在发送什么类型的数据。根据发送的数据类型,浏览器和服务器会采取适应的处理方式。 "multipart/form-data"是一…...

C++11 新特性:新增算法
C11 在标准库中引入了一系列新的算法,这些新增的算法使我们的代码写起来更简洁方便。 下面是 C11 中新增加的一些重要算法的简要描述和使用方法: 1、非修改序列操作 std::all_of:检查范围内的所有元素是否都满足指定的谓词。std::any_of&a…...
c/c++普通for循环学习
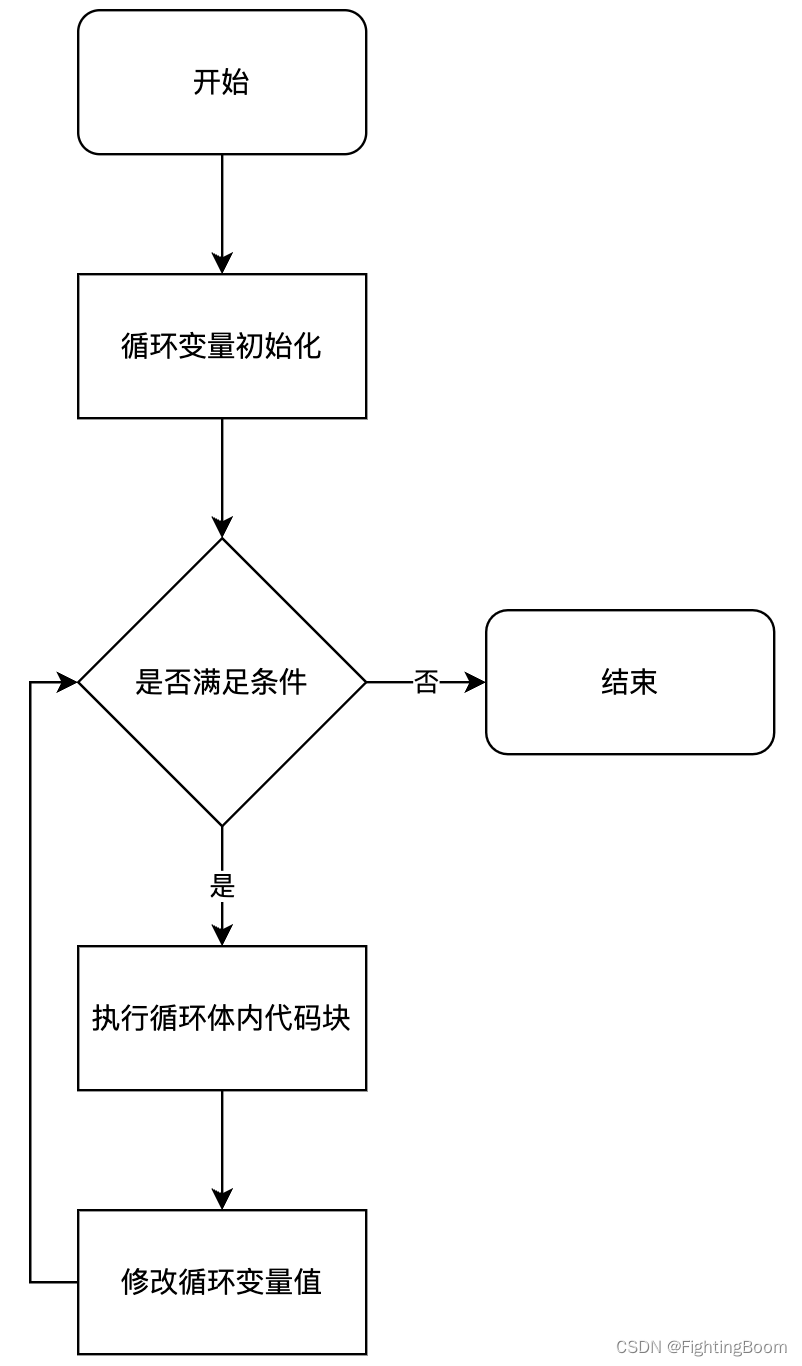
学习一下 for 循环的几种不同方式,了解一下原理及差异 完整的测试代码参考 GitHub :for 循环测试代码 1 常用形态 对于 for 循环来说,最常用的形态如下 for (表达式1; 表达式2; 表达式3) {// code }流程图如下: 编写测试代码…...
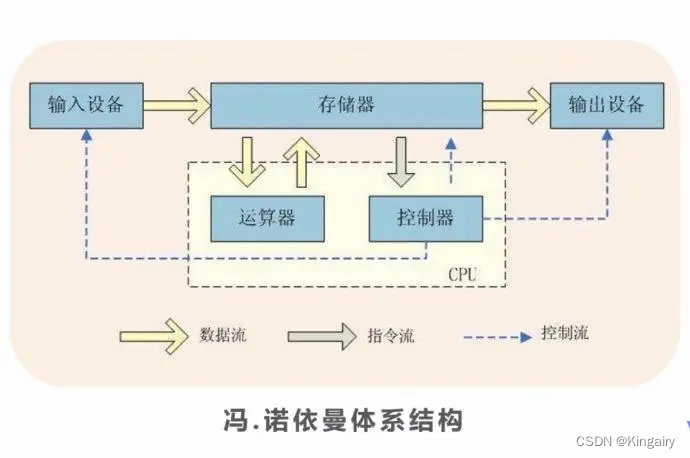
操作系统组成部分
从1946年诞生第一台电子计算机。 冯诺依曼结构 冯诺依曼是:数字计算机的数制采用二进制;计算机应该按照程序顺序执行。 常见的操作系统有三种类型 单用户单任务操作系统:只支持一个用户和一个任务的执行,如DOS;单用…...

深入理解DES算法:原理、实现与应用
title: 深入理解DES算法:原理、实现与应用 date: 2024/4/14 21:30:21 updated: 2024/4/14 21:30:21 tags: DES加密对称加密分组密码密钥管理S盒P盒安全性分析替代算法 DES算法简介 历史 DES(Data Encryption Standard)算法是由IBM研发&…...

# 达梦sql查询 Sql 优化
达梦sql查询 Sql 优化 文章目录 达梦sql查询 Sql 优化注意点测试数据单表查询 Sort 语句优化优化过程 多表关联SORT 优化函数索引的使用 注意点 关于优化过程中工具的选用,推荐使用自带的DM Manage,其它工具在查看执行计划等时候不明确在执行计划中命中…...

Linux下SPI驱动:SPI设备驱动简介
一. 简介 Linux下的SPI 驱动框架和 I2C 很类似,都分为主机控制器驱动和设备驱动,主机控制器也就是 SOC的 SPI 控制器接口,SPI设备驱动也就是所操作的SPI设备的驱动。 本文来学习一下Linux下SPI设备驱动。 二. Linux下SPI驱动:SP…...

【简明图文教程】Node.js的下载、安装、环境配置及测试
文章目录 前言下载Node.js安装Node.js配置Node.js配置环境变量测试后言 前言 本教程适用于小白第一次从零开始进行Node.js的下载、安装、环境配置及测试。 如果你之前已经安装过了Node.js或删除掉了Node.js想重新安装,需要先参考以下博客进行处理后,再根…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

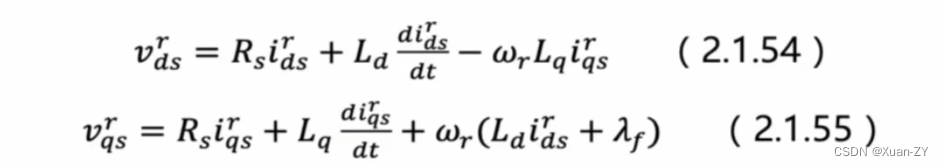
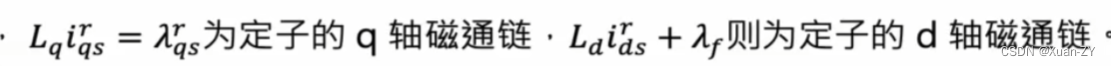 ipmsm转矩方程式:
ipmsm转矩方程式: