Learning Feature Sparse Principal Subspace 论文阅读
1 Abstract:
- 这篇论文提出了新的算法来解决特征稀疏约束的主成分分析问题(FSPCA),该问题同时执行特征选择和PCA。现有的FSPCA优化方法需要对数据分布做出假设,并且缺乏全局收敛性的保证。尽管一般的FSPCA问题是NP难问题,我们展示了对于低秩协方差,FSPCA可以全局解决(算法1)。然后,我们提出了另一种策略(算法2),通过迭代构建一个精心设计的代理来解决一般协方差情况下的FSPCA问题,并保证收敛性。我们为新算法提供了(数据依赖的)近似界限和收敛性保证。对于具有指数/Zipf分布的协方差谱,我们提供了指数/多项式近似界限。实验结果表明,与最先进的方法相比,新算法在合成数据和真实世界数据集上表现出有希望的性能和效率。
2 Object function:

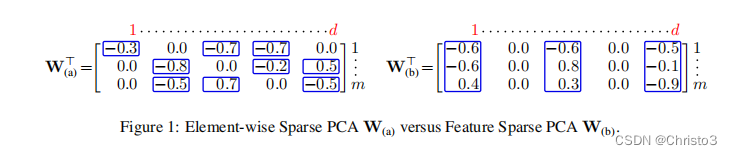
3 Solving strategy:


4 Summarize
-
算法原理可以分为两部分:
低秩协方差矩阵的全局最优解(Algorithm 1):
当协方差矩阵A的秩小于或等于m时,算法可以找到一个全局最优解。这是因为在低秩情况下,可以直接通过选择A中最大的k个特征值对应的特征向量来构建W,从而得到一个最优的稀疏主子空间。
算法首先确定A中最大的k个特征值,并选择对应的特征向量。这些特征向量构成了一个矩阵V,然后通过V与一个选择矩阵S相乘得到最终的W,其中S是根据特征值的大小选择特定行的矩阵。高秩协方差矩阵的迭代代理更新(Algorithm 2):
对于高秩协方差矩阵A,算法采用迭代方法来近似解决FSPCA问题。算法构建一个低秩代理矩阵P,然后用这个P来近似原始问题。
在每次迭代中,算法首先使用当前估计的W来构建代理矩阵Pt。这个代理矩阵Pt是通过AWt(WtAWt)†WtA(其中Wt是当前迭代的W)来计算的,它是一个低秩矩阵,其秩不超过m。
然后,算法使用Algorithm 1来解决代理矩阵Pt的FSPCA问题,得到新的Wt+1。
这个迭代过程继续进行,直到Wt+1与Wt相等,即算法收敛。
论文还提供了对这两个算法的理论分析,包括近似界和收敛保证。特别是,对于具有指数或Zipf分布的协方差矩阵谱,论文提供了相应的近似界。
相关文章:

Learning Feature Sparse Principal Subspace 论文阅读
1 Abstract: 这篇论文提出了新的算法来解决特征稀疏约束的主成分分析问题(FSPCA),该问题同时执行特征选择和PCA。现有的FSPCA优化方法需要对数据分布做出假设,并且缺乏全局收敛性的保证。尽管一般的FSPCA问题是NP难问题ÿ…...

Hibernate入门经典与注解式开发大全
本博文主要讲解介绍Hibernate框架,ORM的概念和Hibernate入门,相信你们看了就会使用Hibernate了! 什么是Hibernate框架? Hibernate是一种ORM框架,全称为 Object_Relative DateBase-Mapping,在Java对象与关系数据库之间建…...
蓝桥杯之注意事项
1.特殊求解的地方 2.一些数学公式 比如二叉树求全深度数值那道题 3.掌握有关库函数 #include<algorithm> 包含sort()函数【排列函数】C sort()排序详解-CSDN博客,next_permutation()函数【求解全排列问题】求解数组大小sizeof(arr…...

ES6 全详解 let 、 const 、解构赋值、剩余运算符、函数默认参数、扩展运算符、箭头函数、新增方法,promise、Set、class等等
目录 ES6概念ECMAScript6简介ECMAScript 和 JavaScript 的关系ES6 与 ECMAScript 2015 的关系 1、let 、 const 、var 区别2、变量解构赋值1、数组解构赋值2、对象解构赋值3、字符串的解构赋值 3、展开剩余运算符1、**展开运算符(...)**2、**剩余运算符(...)** 4、函数的拓展函…...
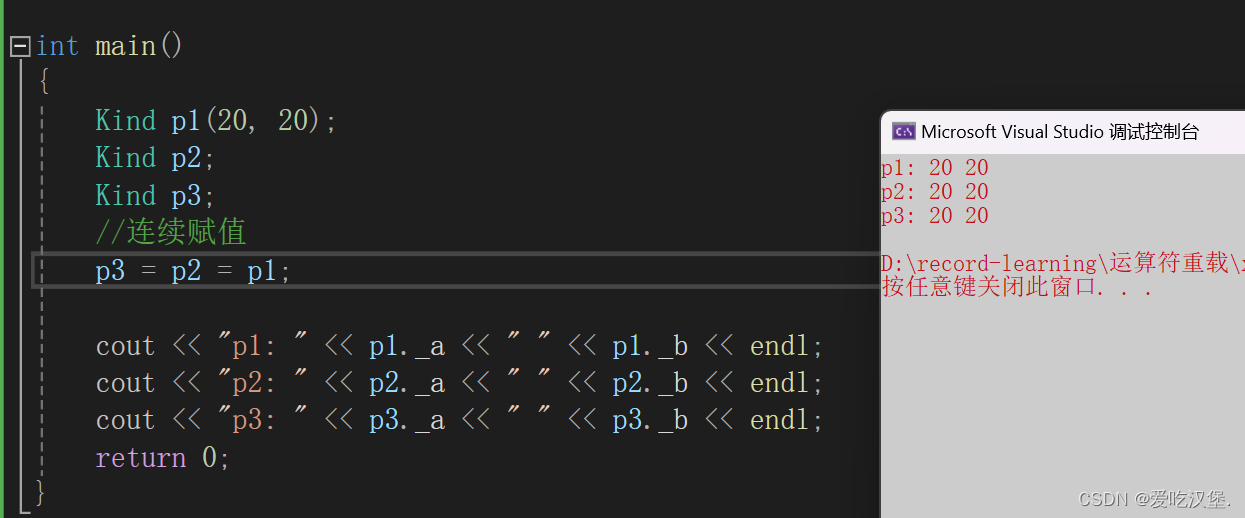
c++ - 类的默认成员函数
文章目录 前言一、构造函数二、析构函数三、拷贝构造函数四、重载赋值操作符五、取地址及const取地址操作符重载 前言 默认成员函数是编译器自动生成的,也可以自己重写,自己重写之后编译器就不再生成,下面是深入了解这些成员函数。 一、构造…...
)
Java哈希查找(含面试大厂题和源码)
哈希查找(Hash Search)是一种基于哈希表(Hash Table)的数据查找方法。哈希表通过使用哈希函数将键(Key)映射到表中的位置来存储数据,从而实现快速的数据访问。哈希查找的效率通常取决于哈希函数…...

c++中常用库函数
大小写转换 islower/isupper函数 char ch1 A; char ch2 b;//使用islower函数判断字符是否为小写字母 if(islower(ch1)){cout << ch1 << "is a lowercase letter." << end1; } else{cout << ch1 << "is not a lowercase lette…...
Scrapy框架 进阶
Scrapy框架基础Scrapy框架进阶 【五】持久化存储 命令行:json、csv等管道:什么数据类型都可以 【1】命令行简单存储 (1)语法 Json格式 scrapy crawl 自定义爬虫程序文件名 -o 文件名.jsonCSV格式 scrapy crawl 自定义爬虫程…...
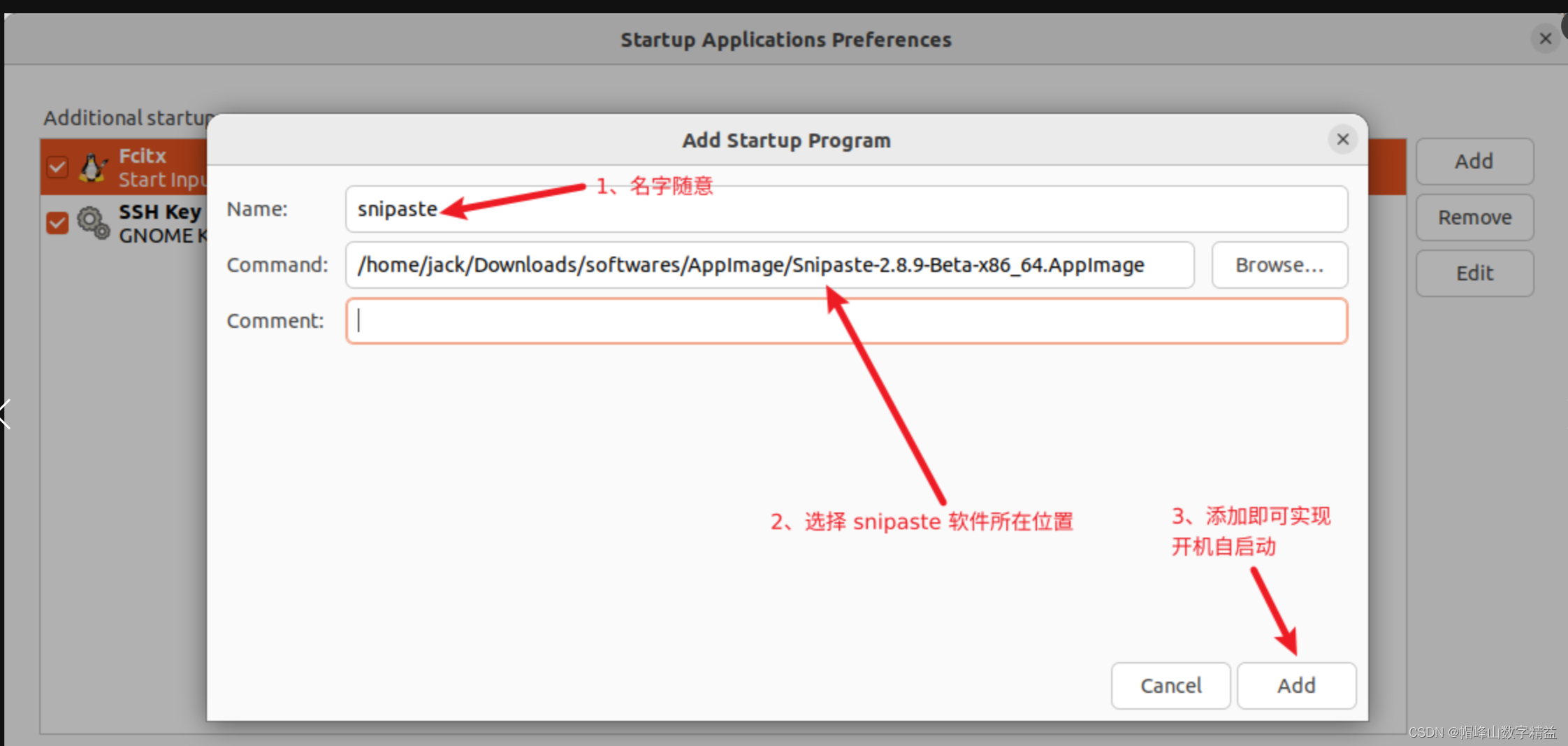
ubuntu22安装snipaste
Ubuntu 22.04 一、Snipaste 介绍和下载 Snipaste 官网下载链接: Snipaste Downloads 二、安装并使用 Snipaste # 1、进入Snipaste-2.8.9-Beta-x86_64.AppImage 目录(根据自己下载目录) cd /home/jack/Downloads/softwares/AppImage# 2、Snipaste-2.8.9-…...
spring-cloud微服务openfeign
Spring Cloud openfeign对Feign进行了增强,使其支持Spring MVC注解,另外还整合了Ribbon和Nacos,从而使得Feign的使用更加方便 优势,openfeign可以做到使用HTTP请求远程服务时就像洞用本地方法一样的体验,开发者完全感…...
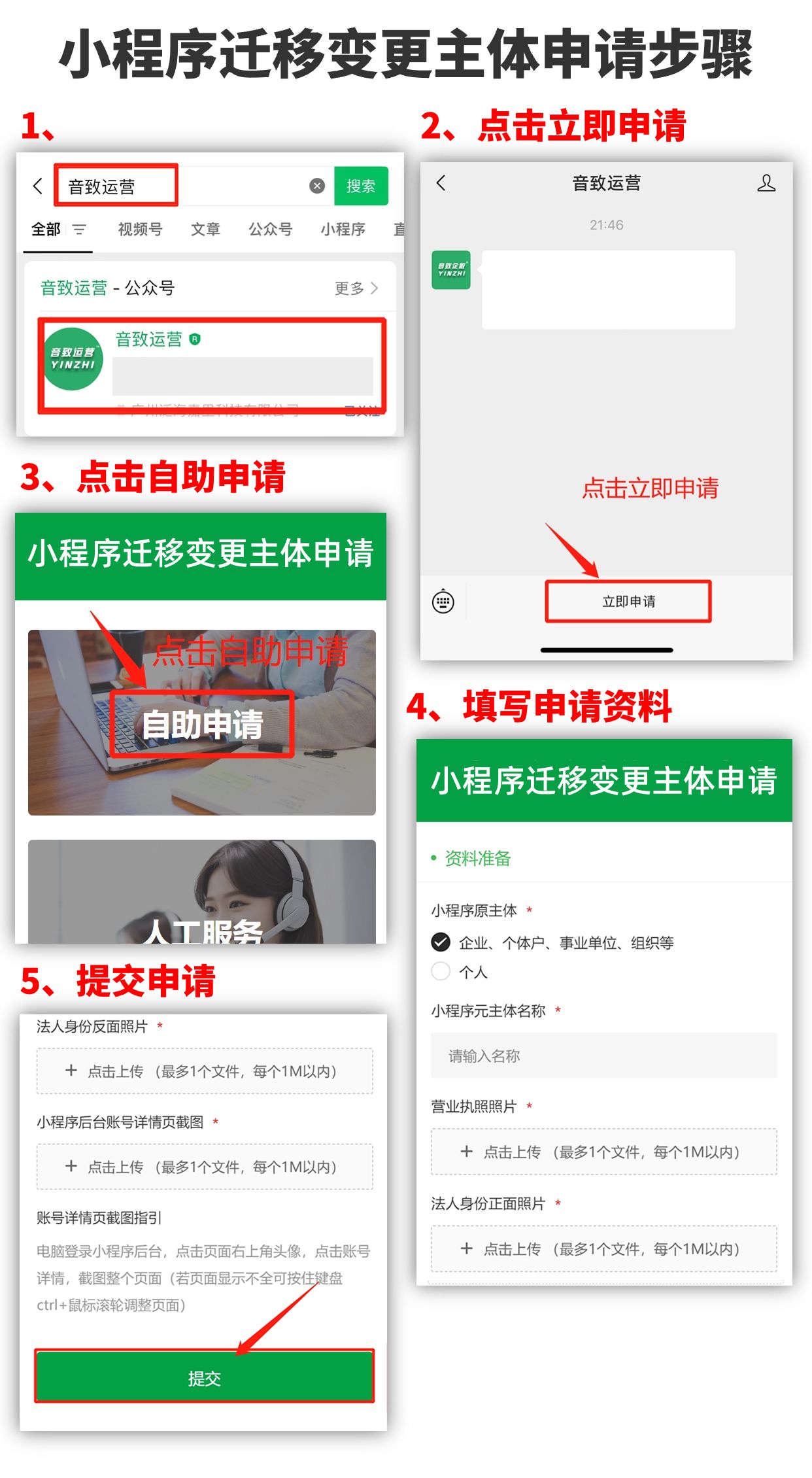
小程序变更主体需要多久?
小程序迁移变更主体有什么作用?小程序迁移变更主体的好处有很多哦!比如可以获得更多权限功能、公司变更或注销时可以保证账号的正常使用、收购账号后可以改变归属权或使用权等等。小程序迁移变更主体的条件有哪些?1、新主体必须是企业主体&am…...

19 Games101 - 笔记 - 相机与透镜
**19 ** 相机与透镜 目录 摘要一 照相机主要部分二 小孔成像与视场(FOV)三 曝光(Exposure)四 景深(Depth of Field)总结 摘要 虽说照相机与透镜属于相对独立的话题,但它们的确是计算机图形学当中的一部分知识。在过往的十多篇笔记中,我们学习的都是如…...

Flink入门学习 | 大数据技术
⭐简单说两句⭐ ✨ 正在努力的小新~ 💖 超级爱分享,分享各种有趣干货! 👩💻 提供:模拟面试 | 简历诊断 | 独家简历模板 🌈 感谢关注,关注了你就是我的超级粉丝啦! &…...

Arthas实战教程:定位Java应用CPU过高与线程死锁
引言 在Java应用开发中,我们可能会遇到CPU占用过高和线程死锁的问题。本文将介绍如何使用Arthas工具快速定位这些问题。 准备工作 首先,我们创建一个简单的Java应用,模拟CPU过高和线程死锁的情况。在这个示例中,我们将编写一个…...

HTML制作跳动的心形网页
作为一名码农 也有自己浪漫的小心思嗷~ 该网页 代码整体难度不大 操作性较强 祝大家都幸福hhhhh 效果成品: 全部代码: <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN"> <HTML><HEAD><TITLE> 一个…...
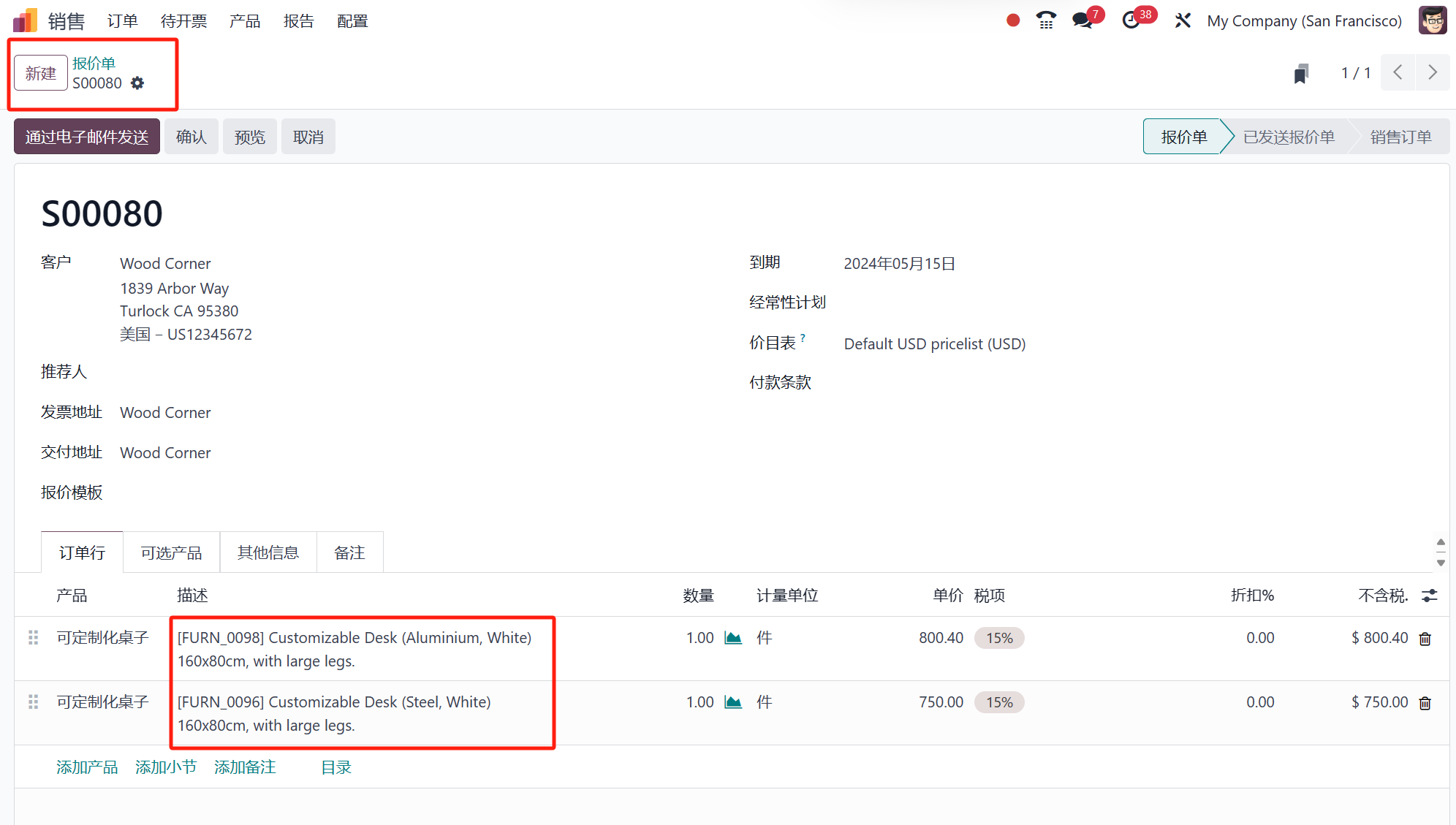
如何在Odoo 17 销售应用中使用产品目录添加产品
Odoo,作为一个知名的开源ERP系统,发布了其第17版,新增了多项功能和特性。Odoo 17包中的一些操作简化了,生产力提高了,用户体验也有了显著改善。为了为其用户提供新的和改进的功能,Odoo不断进行改进和增加新…...

为什么pdf拆分出几页之后大小几乎没有变化
PDF 文件的大小在拆分出几页之后几乎没有变化可能有几个原因: 图像压缩: 如果 PDF 文件中包含图像,而这些图像已经被压缩过,拆分后的页面依然会保留这些压缩设置,因此文件大小可能不会显著变化。 文本和矢量图形: PDF 文件中的文…...
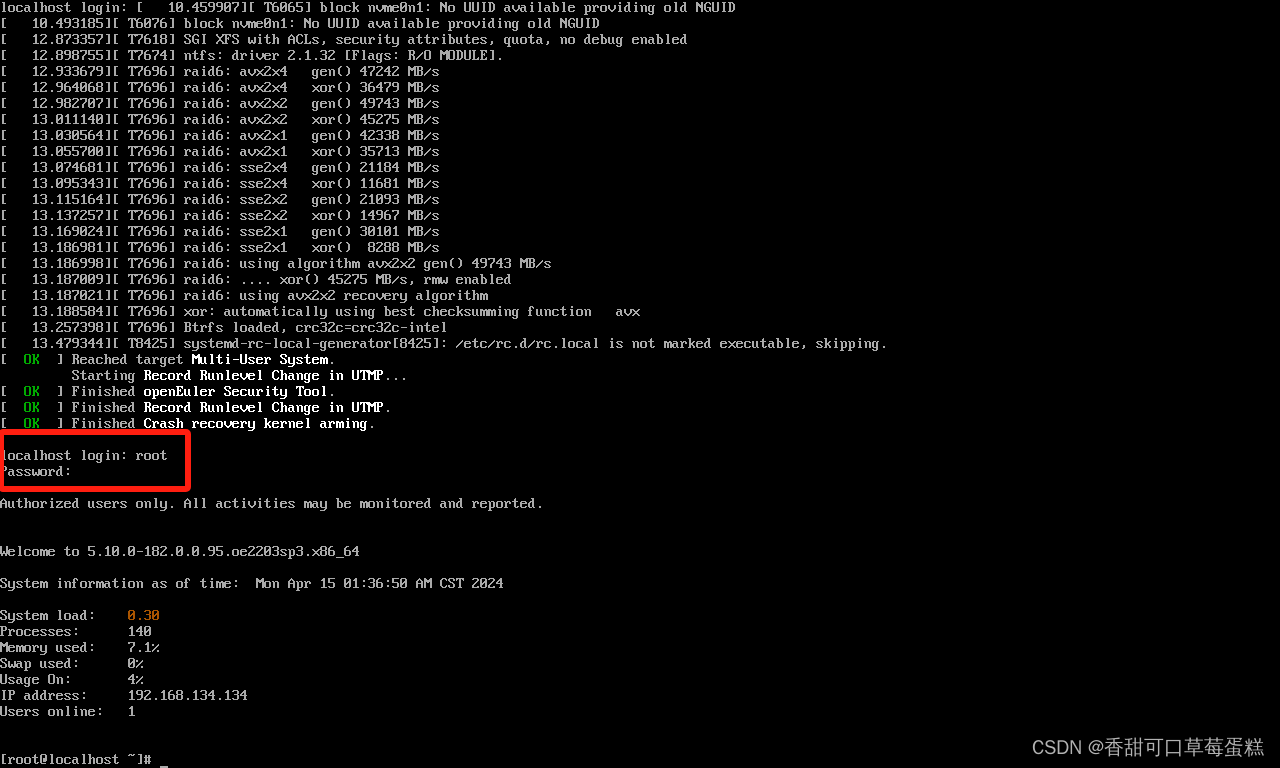
如何在 VM 虚拟机中安装 OpenEuler 操作系统保姆级教程(附链接)
一、VMware Workstation 虚拟机 若没有安装虚拟机的可以参考下篇文章进行安装: 博客链接https://eclecticism.blog.csdn.net/article/details/135713915 二、OpenEuler 镜像 点击链接前往官网 官网 选择第一个即可 三、安装 OpenEuler 打开虚拟机安装 Ctrl …...

(六)PostgreSQL的组织结构(3)-默认角色和schema
PostgreSQL的组织结构(3)-默认角色和schema 基础信息 OS版本:Red Hat Enterprise Linux Server release 7.9 (Maipo) DB版本:16.2 pg软件目录:/home/pg16/soft pg数据目录:/home/pg16/data 端口:57771 默认角色 Post…...

DockerFile定制镜像
dockerfile 简介 Dockerfile 是⼀个⽤来构建镜像的⽂本⽂件,⽂本内容包含了⼀条条构建镜像所需的指令和 说明,每条指令构建⼀层,最终构建出⼀个新的镜像。 docker镜像的本质是⼀个分层的⽂件系统 centos的iso镜像⽂件是包含bootfs和rootfs…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
